Geometry Chapter 4 Pythagoras Theorem
- In any right-angled triangle, the area of the square drawn on the hypotenuse is equal to the sum of the areas of the squares drawn on the other two sides.
- If in a triangle, the area of a square drawn on one side is equal to the sum of the areas of squares drawn on other two sides, then the angle opposite to the first side will be right angle.
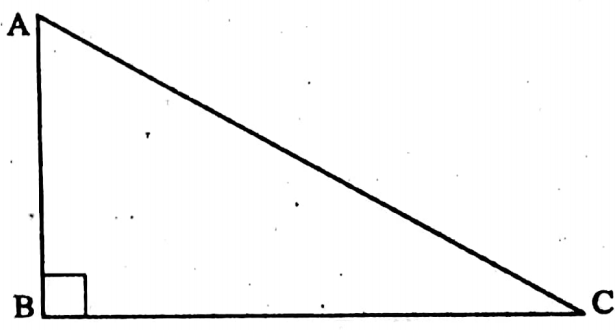
In ΔABC, ∠ABC = 90°
∴ AC2 = AB2 + BC2
Read and Learn More WBBSE Solutions for Class 10 Maths

Geometry Chapter 4 Pythagoras Theorem True Or False
Example 1. If the ratio of the lengths of three sides of a triangle is 3: 4: 5, then the triangle will always be a right-angled triangle.
Solution: Let the length of three sides are 3x unit, 4x unit and 5x units
[x is a common multiple and x > 0]
(3x)2 + (4x)2 = 9x2 + 162 = 25x2 = (5x)2
∴ The triangle is right angled triangle.
∴The statement is true.
Example 2. If in a circle of radius 10 cm in length, a chord subtends right angle at the centre, then the length of the chord will be 5 cm.
Solution: Let PQ is a chord of a circle with centre O;

OP = OQ = 10 cm and ∠POQ = 90°
In right angled triangle POQ, PQ2 = OP2 + OQ2
∴ PQ = \(\sqrt{O P^2+O Q^2}\)
= \(\sqrt{10^2+10^2} \mathrm{~cm}\)
= √200 cm = 10√2 cm
∴ length of chord PQ is 10√2
∴ The given statement is false.
Geometry Chapter 4 Pythagoras Theorem Fill In The Blanks
Example 1. In a right-angled triangle, the area of a square drawn on the hypotenuse is equal to the _____ of the areas of the squares drawn on other two sides.
Solution: sum
Example 2. In an isosceles right-angled triangle if the length of each of two equal sides is 4√2 cm then the length of the hypotenuse will be _______ cm.
Solution: In a right-angled triangle ABC,
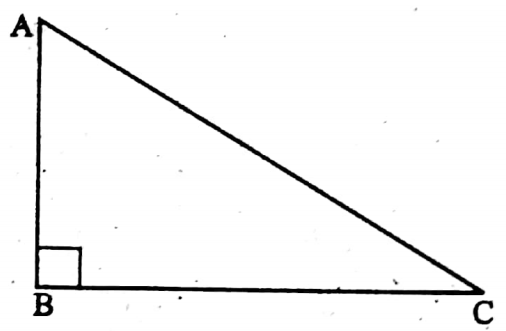
AB = BC = 4√2 cm and ∠ABC = 90°.
AC2 = AB2 + BC2
⇒ AC = \(\sqrt{A B^2+B C^2}=\sqrt{(4 \sqrt{2})^2+(4 \sqrt{2})^2 \mathrm{~cm}}\)
= \(\sqrt{32+32} \mathrm{~cm}=\sqrt{64} \mathrm{~cm}=8 \mathrm{~cm}\)
∴ The length hypotenuse will be 8 cm.
Class 10 Maths Geometry Chapter 4 Solutions
Example 3. In a rectangular ABCD, the two diagonals AC and BD intersect each other at the point O, if AB = 12 cm, AO = 6.5 cm, then the length of BC is _______ cm.
Solution: AC and BD are bisects each other.

∴ OC = OA = 6.5 cm
∴ AC = (6.5 x 2) cm = 13 cm
In right angle ΔABC, ∠ABC = 90°
∴ AB2 + BC2 = AC2 [By Pythagoras theorem]
⇒ BC = \(\sqrt{A C^2-A B^2}\)
= \(\sqrt{13^2-12^2} \mathrm{~cm}\)
= √25 cm = 5 cm
∴ 5 cm
Geometry Chapter 4 Pythagoras Theorem Short Answer Type Question
Example 1. In ΔABC, if AB = (2a – 1) cm, AC = 2√2a cm and BC = (2a + 1) cm, then write the value of ∠BAC.
Solution:

AB2 = (2a – 1)2
AC2 = (2√2a)2 = 8a
BC2 = (2a + 1)2
AB2 + AC2 = (2a – 1)2 + 8a
= (2a – 1)2 + 4.2a.1 = (2a + 1)2
∴ AB2 + AC2 = BC2
∴ ΔABC is a right-angled triangle whose hypotenuse is BC
∴ ∠BAC = 90°
Example 2. Point O has situated within P the triangle PQR in such a way that ∠POQ = 90°, OP = 6 cm and OQ = 8 cm. Write the length of QR.
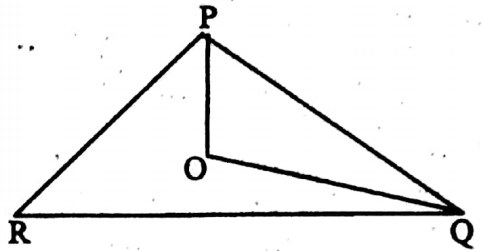
Solution: In a right-angled triangle POQ, ∠POR = 90°
∴ PQ2 = OP2 + OQ2
⇒ PQ = \(\sqrt{O P^2+O Q^2}\)
= \(\sqrt{6^2+8^2} \mathrm{~cm}=\sqrt{100} \mathrm{~cm}=10 \mathrm{~cm}\)
In right-angled ΔPQR, ∠QPR = 90°
∴ QR2 = PQ2 + PR2
QR = \(\sqrt{\mathrm{PQ}^2+\mathrm{PR}^2}\)
= \(\sqrt{10^2+24^2} \mathrm{~cm}=\sqrt{676} \mathrm{~cm}=26 \mathrm{~cm}\)
Example 3. The point O is situated within the rectangular figure ABCD in such a way that OB = 6cm, OD = 8 cm and OA = 5 cm. Determine the length of OC.
Solution: I draw a parallel line PQ through O which intersects AD and BC of P and Q respectively.

In quadrilateral ABQP, AB || PQ and AP || BQ.
∴ ABQP is a parallelogram ∴ AP = BQ
Similarly, CDPQ is a parallelogram ∴ CQ = DP
In right-angled triangle AOP, ∠APO = 90°
∴ OA2 = AP2 + OP2
Similarly, In ΔCOQ, OC2 = CQ2 + OQ2
In ΔBOQ, OB2 = BQ2 + OQ2
and In ΔDOP, OD2 = DP2 + OP2
OA2 + OC2 = AP2 + CQ2 + OP2 + OQ2
= BQ2 + DP2 + OP2 + OQ2 [AP = BQ; CQ = D]
= (BQ2 + OQ2) + (DP2 + OP2)
OA2 + OC2 = OB2 + OD2
⇒ OC = \(\sqrt{O B^2+O D^2-O A^2}\)
= \(\sqrt{6^2+8^2-5^2} \mathrm{~cm}=\sqrt{75} \mathrm{~cm}=5 \sqrt{3} \mathrm{~cm}\)
∴ Length of OC is 5√3 cm.
Areas Related To Circles Class 10 Solutions
Example 4. In the triangle ABC the perpendicular AD from the point A BC at the point D. If BD = 8 cm, DC = 2 on the side BC meets the side BC at the point D. If BD = 8 cm, DC = 2 cm and AD = 4 cm, then write the measure of ∠BAC.
Solution: In ΔABD, ∠ADB = 90°cm [∵ AD ⊥ BC]
AB2 = BD2 + AD2
= {(8)2 + (4)2} sq. cm = 100 sq. cm

In ΔACD, ∠ADC = 90°
∴ AC2 = AD2 + DC2
= {(4)2 + (2)2} sq. cm = 20 sq. cm
AB2 + AC2 = (100 + 20) sq. cm = 100 sq. cm
BC2 = (BD + DC)2 = (8 + 2)2 sq. cm = 100 sq. cm
∵ AB2 + AC2 = BC2
∴ ΔABC is right angled triangle whose hypotenuse is BC
∴ ∠BAC = 90°
Example 5. In the right-angled triangle, ABC, ∠ABC = 90°, AB = 3 cm, BC = 4 cm and the perpendicular BD on the side AC from the point B which meets the side AC at the point D. Determine the length of BD.
Solution:

In ΔABC, ∠ABC = 90°
AC2 = AB2 + BC2
AC = \(\sqrt{\mathrm{AB}^2+\mathrm{BC}^2}=\sqrt{3^2+4^2} \mathrm{~cm}=\sqrt{25} \mathrm{~cm}=5 \mathrm{~cm}\)
let, AD = x cm [x>0]
CD = (5 – x) cm
In, ΔABD, BD2 = AB2 – AD2
In ΔBCD, BD2 = BC2 – DC2
∴ AB2 – AD2 = BC2 – DC2
32 – x2 = 42 – (5 – x)2
⇒ 9 – x2 = 16 – 25 + 10x – x2
⇒ 10x = 18
⇒ x = 1.8
∴ AD = 1.9 cm
BD = \(\sqrt{\mathrm{AB}^2-\mathrm{AD}^2}=\sqrt{(3)^2-(1 \cdot 8)^2} \mathrm{~cm}\)
= \(\sqrt{9-3 \cdot 24} \mathrm{~cm}=\sqrt{5 \cdot 76} \mathrm{~cm}=2 \cdot 4 \mathrm{~cm}\)
∴ The length of BD is 2.4 cm.
Example 6. The length of the hypotenuse of a right-angled triangle is 13 cm and the difference in length of other two sides is 7 cm. Find the perimeter of the triangle.
Solution: In right-angled ΔABC, ∠ABC = 90°
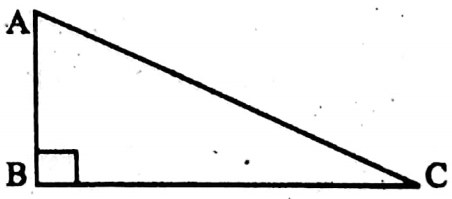
hypotenuse (AC) = 13 cm and AB = AB = x cm [x > 0]
let AB < BC
∴ BC = (x + 7) cm
In ΔABC, AB2 + BC2 = AC2 [By Pythagoras theorem]
x2 + (x + 7)2 = (13)2
⇒ x2 + x2 + 14x + 49 – 169 = 0
⇒ x2 + 7x – 60 = 0
⇒ x2 + 12x- 5x- 60 = 0
⇒ x (x + 12) – 5 (x + 12) = 0
⇒ (x + 12) (x- 5) = 0
either x + 12 = 0
⇒ x =- 12
or, x- 5 = 0
⇒ x = 5
as x > 0
∴ Length of two sides are 5 cm and (5 + 7) cm and 12 cm.
∴ Perimeter of the triangle is (5 + 12 + 13) cm i.e. 30 cm.
Class 10 Geometry Chapter 4 Solved Examples
Example 7. A square is inscribed in a circle with radius 2 cm in length. Find the perimeter of the square.
Solution: ABCD is a cyclic square and the centre of the circle is O; AC is a diagonal of the square and also AC is the diameter of the circle.
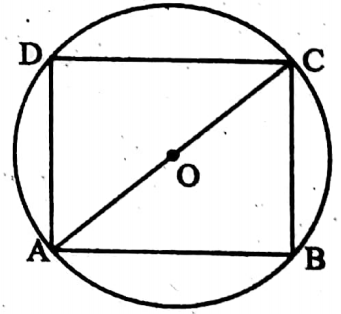
∴ AC = (2 x 2) cm = 4 cm
Let, AB = BC = CD = DA = x cm [x > 0]
In ΔABC, ∠ABC = 90°
∴ AB2 + BC2 = AC2
x2 + x2 = (4)2.
⇒ 2x2 = 16
⇒ x = √8 = 2√2
∴ Perimeter of the square is (4 x 2√2) cm or 8√2 cm
Example 8. The length of two equal sides of an isosceles triangle are (x + 2) cm and (2x – 1) cm. Find out the circumradius of the triangle.
Solution: ΔABC is an isosceles triangle whose ∠ABC = 90° and AB = B

Let AB = (x + 2) cm and BC = (2x- 1) cm
∴ 2x – 1- x + 2 ⇒ x = 3
∴ AB = BC = (3 + 2) cm = 5 cm
ΔABC, ∠ABC = 90°
∴ AC2 = AB2 + BC2
⇒ AC = \(\sqrt{\mathrm{AB}^2+\mathrm{BC}^2}=\sqrt{5^2+5^2} \mathrm{~cm}\)
= \(\sqrt{50} \mathrm{~cm}=5 \sqrt{2} \mathrm{~cm}\)
∴ The circumradius of ΔABC is \(\frac{5 \sqrt{2}}{2}\) cm
Wbbse Class 10 Geometry Notes
Example 9. The length of a side of a rectangle is a unit and length of one diagonal is \(\sqrt{a^2+b^2}\) unit. What is the area of the rectangle?
Solution: AB unit and AC = \(\sqrt{a^2+b^2}\) unit of rectangle ABCD.

Let BC = x unit
In a right-angled triangle ABC, ∠ABC = 90°
∴ AB2 + BC2 = AC2
BC = \(\sqrt{\mathrm{AC}^2-\mathrm{AB}^2}\)
= \(\sqrt{\left(\sqrt{a^2+b^2}\right)^2-a^2} \text { unit }\)
= \(\sqrt{a^2+b^2-a^2} \text { unit }=\sqrt{b^2} \text { unit }=b \text { unit }\)
∴ Area of the rectangle is = (a x b) sq. unit = ab sq. unit
Example 10. The lengths of two adjacent sides of right angle of a right-angled triangle are 16 cm and 12 cm. Find the length of the radius of incircle of the triangle.
Solution: In ΔABC, ∠ABC = 90°
AB = 12 cm, BC = 16 cm, AC2 = AB2 + BC2
AC = \(\sqrt{\mathrm{AB}^2+\mathrm{BC}^2}=\sqrt{12^2+16^2}\) = √400 cm = 20 cm
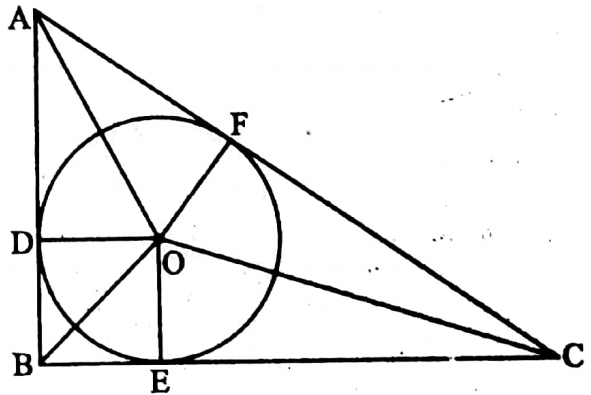
Let length of radius of incircle of a triangle ABC is r cm.
∴ OD = OE = OF = r cm
ΔAOB + ΔBOC + ΔCOA = ΔABC
\(\frac{1}{2}\) x AB x OD + \(\frac{1}{2}\) x BC x OE + \(\frac{1}{2}\) x AC x OF = \(\frac{1}{2}\) x BC x AB
⇒ AB x OD + BC + OE + AC x OF = BC x AB
∴ 12 x r + 16 x r + 20 x r = 16 x 12
⇒ r = 4
∴ The length of radius of the circle is 4 cm.
Example 11. If semi perimeter of an equilateral triangle is 7.5 cm then calculate the area of the triangle.
Solution: Perimeter of the equlateral triangle ABC is (7.5 x 2) cm or 15 cm
∴ AB = BC = CA = \(\frac{15}{3}\) cm = 5 cm
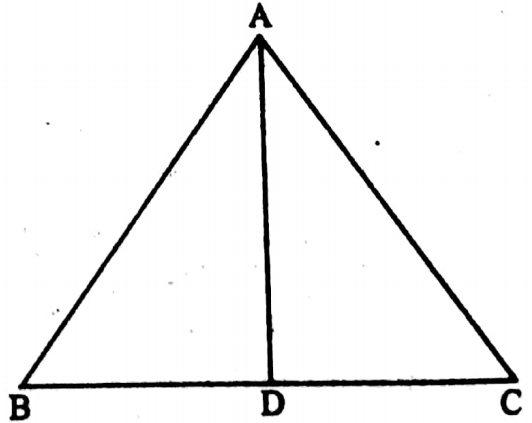
I draw AD ⊥ BC
In ΔABD and ΔACD,
AB = AC, ∠ABD = ∠ACD = 60° and ∠ADB = ∠ADC = 90°
∴ ΔABD ≅ ΔACD,
∴ BD = CD = \(\frac{5}{2}\) cm = 2.5 cm
In ΔABD, AD2 + BD2 = AB2
⇒ \(\mathrm{AD}=\sqrt{\mathrm{AB}^2-\mathrm{BD}^2}=\sqrt{5^2-\left(\frac{5}{2}\right)^2} \mathrm{~cm}=\sqrt{\frac{75}{4}} \mathrm{~cm}=\frac{5 \sqrt{3}}{4} \mathrm{~cm}\)
Area of ΔABC = \(\frac{1}{2}\) x BC x AD = \(\frac{1}{2}\) x 5 x \(\frac{5 \sqrt{3}}{2}\) sq cm = \(\frac{25 \sqrt{3}}{4}\) sq. cm
Area And Perimeter Of Circles Class 10
Example 12. BC is a diameter of the semicircle with centre O. If AB = (x + 3) cm, AC = (5x + 2) cm and BC = (7x – 1) cm, then find the length of the radius of the semicircle, [x > 0]
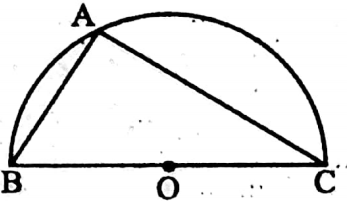
Solution: ∠BAC = 90° [semicircular angle]
In a right-angled triangle, ABC, BC2 = AB2 + AC2
⇒ (7x- 1)2 = (x + 3)2 + (5x + 2)2
⇒ 49x2 – 14x + 1 = x2 + 6x + 9 + 25x2 + 20x + 4
⇒ 23x2 – 40x – 12 = 0
⇒ 23x2 – 46x + 6x – 12 = 0
⇒ 23x (x- 2) + 6 (x – 2) = 0
⇒ (x- 2) (23x + 6) = 0
either x- 2 = 0
⇒ x = 2
as x > 0, ∴ x = 2
or, 23x + 6 = 0
⇒ x = –\(\frac{6}{23}\)
∴ BC = (7 x 2 – 1) cm = 13 cm
∴ The length of radius is \(\frac{13}{2}\) cm or 6.5 cm.
Example 13. If the perimeter of isosceles right angled triangle is √2(√2 +1) cm, then calculate the area of the triangle.
Solution: Let in ΔABC, AB = BC = x cm [x > 0]
and ∠ABC = 90°
∴ AC2 = AB2 + BC2
⇒ AC = \(\mathrm{AC}=\sqrt{\mathrm{AB}^2+\mathrm{BC}^2}=\sqrt{x^2+x^2} \mathrm{~cm}=\sqrt{2} x \mathrm{~cm}\)
Perimeter = (x + x + √2 x) cm
= (2x + √2x) cm = √2 (√2 + 1)x
According to question, √2(√2 + 1)x = √2 (√2 + 1)
⇒ x = 1
AB = BC = 1 cm
Area of ΔABC = \(\frac{1}{2}\) x BC x AB (\(\frac{1}{2}\) x 1 x 1)sq. cm = \(\frac{1}{2}\) sq. cm
Class 10 Maths Geometry Important Questions
Example 14. AB is a chord and AT is a tangent at A of a circle with centre O and OP ⊥ AB. If OP = 3 cm, AB = 8 cm and AT = 12 cm then find the length of OT.

Solution: ∵ OP ⊥ AB
∴ AP = BP = \(\frac{1}{2}\) AB = (\(\frac{1}{2}\) x 8) cm = 4 cm
In ΔAOP, ∠APO = 90°
∴ OA2 = OP2 + AP2
⇒ \(\mathrm{OT}=\sqrt{\mathrm{OA}^2+\mathrm{AT}^2}=\sqrt{5^2+12^2} \mathrm{~cm}=13 \mathrm{~cm}\)
AT is a tangent at A and OA is radius of the circle
∴ OA ⊥ AT, ∴ ∠OAT = 90°
In ΔAOT, OT2 = OA2 + AT2.
⇒ OT = \(\sqrt{\mathrm{OA}^2+\mathrm{AT}^2}=\sqrt{5^2+12^2}\) = 13 cm
Class 10 Maths Geometry Important Questions
Example 15. The ratio of angles of a triangle is 1: 2 : 3; if the length of the biggest sides is 10 cm, find the lengths of the other two sides.
Solution:
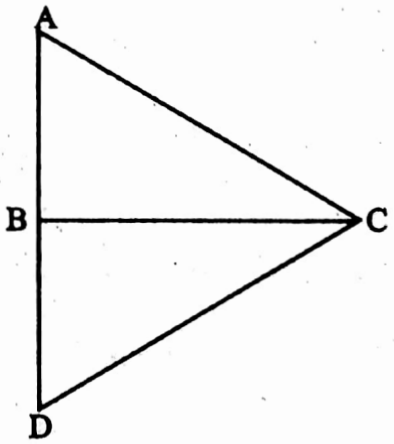
Ratio of angles of a triangle is 1: 2 : 3
∴ The value of 1st angle is \(\left(180^{\circ} \times \frac{1}{1+2+3}\right)\) or 30°
The value of 2nd angle is \(\left(180^{\circ} \times \frac{2}{1+2+3}\right)\) or 60°
and that of third angle is { 180° – (30° + 60°)} or 90°
Let, in ΔABC, ∠ABC = 90°, ∠BAC = 60° and ∠ACB = 30°
∴ AC = 10 cm [the biggest side]
AB is extended to BD such that AB = BD; I join C, D
In ΔABC and ΔDBC, AB = BD, ∠ABC = ∠DBC = 90° and BC = BC [common side]
∴ ΔABC ≅ ΔDBC, ∴ ∠D = ∠A = 60° and ∠BCD = ∠ACB = 30°
∴ ∠ACD = 30° + 30° = 60°
In ΔACD, ∠DAC = ∠ACD = ∠ADC = 60°
∴ ΔACD is an equilateral triangle
∴ AD = AC = 10 cm
AB = \(\frac{1}{2}\) AD = (\(\frac{1}{2}\) x 10) cm = 5 cm
In ΔABC, AB2 + BC2 = AC2
⇒ BC = \(\sqrt{\mathrm{AC}^2-A B^2}=\sqrt{10^2-5^2} \mathrm{~cm}=\sqrt{75} \mathrm{~cm}=5 \sqrt{3} \mathrm{~cm}\)
∴ The length of other two sides are 5 cm and 5√3 cm.
