Geometry Chapter 2 Transversal And Mid Point Theorem
Theorem:
- The line segment joining the midpoints of two sides of a triangle is parallel to the third side and equal to half of it.
- In any triangle, through the midpoint of any side, if a line segment is drawn parallel to the second side, then it will bisect the third side and the length of the line segment intersected by the two sides of the triangle is equal to the length of the half of the second side.
- If three or more parallel straight lines make equal intercepts from a transversal, then they will make equal intercepts from another transversal.
[Proof of the Theorem (3) is not for evaluation]
Read and Learn More WBBSE Solutions For Class 9 Maths
Geometry Chapter 2 Transversal And Mid Point Theorem True Or False
Example 1. In ΔABC, D, and E are the midpoints of AB and AC respectively. If the length of DE is 5 cm, then the length of BC is 10 cm.
Solution: In ΔABC, D and E are the midpoints of AB and AC respectively

∴ DE = \(\frac{1}{2}\) BC
⇒ BC = 2 DE (2 × 5) cm = 10 cm
⇒ So the statement is true.
Example 2. In the equilateral triangle ABC, D, E, and F are midpoints of side AB, BC, and CA respectively. If the perimeter of ΔDEF is 8 cm.
Solution: AB = BC = CA = \(\frac{12}{3}\) cm = 4 cm
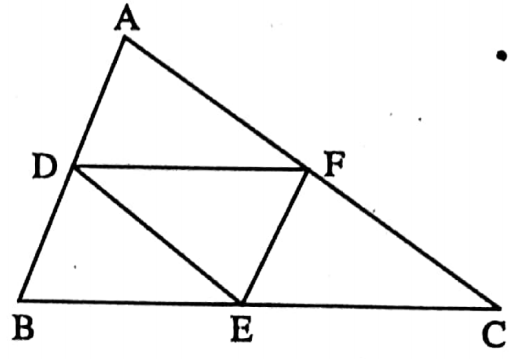
⇒ D and F are midpoints of AB and AC.
∴ DF = \(\frac{1}{2}\) BC = (\(\frac{1}{2}\) x 4) cm = 2 cm
⇒ Similarly, EF = DE = 2 cm
∴ The perimeter of ΔDEF is (2 × 3) cm = 6 cm
∴ The statement is false.
Geometry Chapter 2 Transversal And Mid Point Theorem Fill In The Blanks
Example 1. If three or more _______ straight lines make equal intercepts from a transversal, then they will make equal intercepts from another transversal.
Solution: Parallel.

⇒ [If AB || CD || EF and MN = NO then GH = HI]
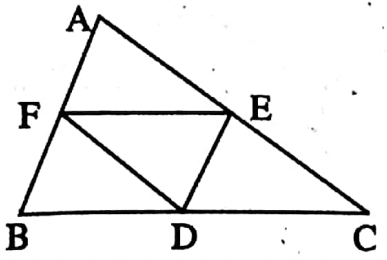
Example 2. The triangle formed by joining midpoints of consecutive sides of an equilateral triangle is a _______ triangle.
Solution: Equilateral.
Geometry Chapter 2 Transversal And Mid Point Theorem Short Answer Type Questions
Example 1. In the triangle, ABC, AD, and BE are two medians and DF is parallel to BE, meets AC at the point F. If the length of the side AC is 8 cm. Find the length of the side CF.
Solution: In ΔBCE, D is the midpoint of BC and DF || BE;

∴ F is the midpoint of EC,
∴ CF = \(\frac{1}{2}\) EC = \(\frac{1}{2}\) x \(\frac{1}{2}\) AC [Midpoint of AC is E]
= \(\frac{1}{4}\) AC = (\(\frac{1}{4}\) x 8) cm
∴ CF = 2 cm.
∴ The length of the side CF is 2 cm.
Example 2. In the triangle, ABC, the midpoints of BC, CA, and AB are P, Q, and R respectively, if AC = 21 cm, BC = 29 cm, and AB = 30 cm perimeter of the quadrilateral ΔRPQ.
Solution: In ΔABC, P and Q are the midpoints of BC and AC respectively.
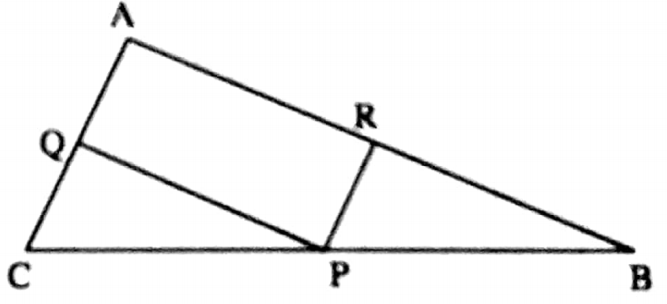
∴PQ = \(\frac{1}{2}\)AB = (\(\frac{1}{2}\)x 30)cm = 15 cm
⇒ Similarly, RP = \(\frac{1}{2}\) AC = \(\frac{1}{2}\)(21) cm = 10.5 cm
⇒ Again AR = \(\frac{1}{2}\) AB = (\(\frac{1}{2}\) x 30) cm = 15 cm
⇒ AQ = \(\frac{1}{2}\)AC = (\(\frac{1}{2}\) x 21)cm = 10.5 cm
∴ Perimeter of quadrilateral ARPQ is AR+ RP+ PQ+ AQ
= (15+ 10.5 + 15 + 10.5)cm = 51 cm
Example 3. In the triangle, ABC, D is any point on the side AC. The midpoints of AB, BC, AD, and DC are P, Q, X, and Y respectively. If PX = 5 cm, then write the length of the side QY.
Solution: XY = DX + DY
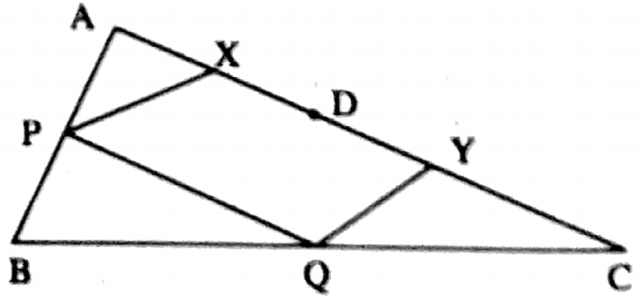
= \(\frac{1}{2}\) AD + \(\frac{1}{2}\) DC
= \(\frac{1}{2}\)(AD + DC)
= \(\frac{1}{2}\) AC
In ΔABC, P and Q are the midpoints of AB and BC
∴ PQ = \(\frac{1}{2}\) AC and PQ || AC
∴ XY = PQ and PQ || XY [PQ || AC]
∴ PQYX is a parallelogram
∴ QY= PX = 5 cm.
∴ The length of the side QY is 5 cm.
Example 4. In the triangle ABC, the medians BE and CF intersects at the point G. The midpoints of BG and CG are P and Q respectively. If PQ = 3 cm, then find the length of BC.
Solution: In ΔGBC, the midpoints of BG and CG are P and Q respectively.
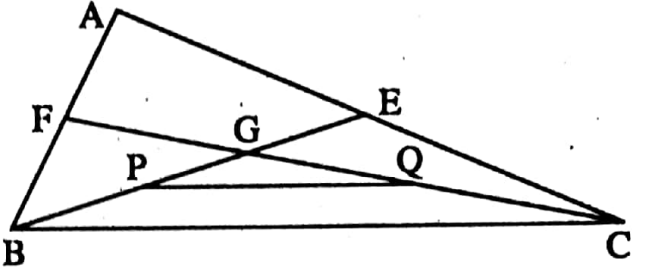
∴ PQ = \(\frac{1}{2}\) BC
⇒ BC = 2 PQ = (2 x 3) cm = 6 cm.
∴ The length of BC is 6 cm.
Example 5. In the triangle ABC, the midpoints of BC, CA, and AB are D, E, and F respectively, EF intersects AD at the point O. If AD = 6 em, then write the length of AO.
Solution: In ΔABC, F, and E are the midpoints of AB and AC respectively.
= FE || BC
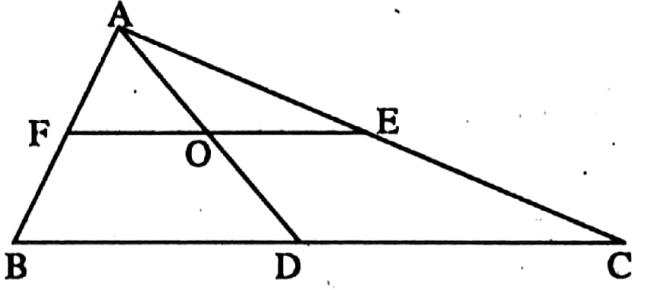
⇒ In ΔABD, F is the midpoint of AB and FO || BD [FE || BC]
∴ O is the midpoint of AD
∴ AO = \(\frac{1}{2}\) AD = (\(\frac{1}{2}\) x 6) cm = 3 cm
∴ The length of AO is 3 cm.
Example 6. In the parallelogram ABCD, BC is extended to point P such that BC CP. Join A, P; AP is intersect CD and BD at the points Q and R respectively. If DR = 3 cm then find the length of BR.
Solution: Through point C a line segment parallel to BD is drawn which intersects AP at the point S.
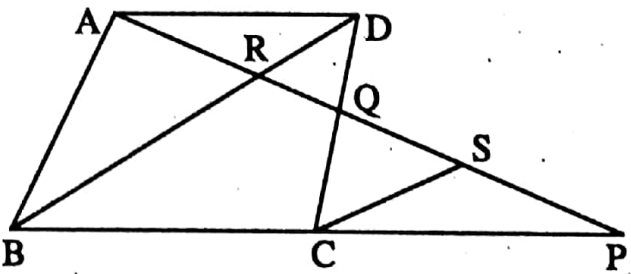
⇒ In parallelogram ABCD, AD = BC
⇒ Again, BC = CP ∴ AD = CP.
⇒ In ΔADQ and ΔCPQ,
⇒ ∠AQD = ∠CQP [vertically opposite angles]
⇒ ∠DAQ alternate ∠CPQ [AD || BP and AP is intersection]
and AD = CP
∴ ΔADQ ≅ ΔCPQ ∴ DQ = CQ
⇒ In ΔDQR and ΔCQS
⇒ ∠DQR = ∠CQS [vertically opposite angles]
⇒ ∠RDQ = alternate ∠SCQ and DQ = CQ
∴ ∠DQR ≅ ΔCQS, ∴ DR = CS
⇒ In ΔBPR, C is the midpoint of BP and CS || BR
∴ CS = \(\frac{1}{2}\) BR
⇒ or, BR = 2 CS = 2 DR (2 x 3) cm = 6 cm.
∴ The length of BR is 6 cm.
Example 7. In the triangle, ABC, D, and E are the midpoints of AB and BC respectively. BC is extended to the point F such EC CF; Join D, F. If AC = 8 cm, then find the length of CG.
Solution: In ΔABC, D, and E are the midpoints of AB and BC respectively.
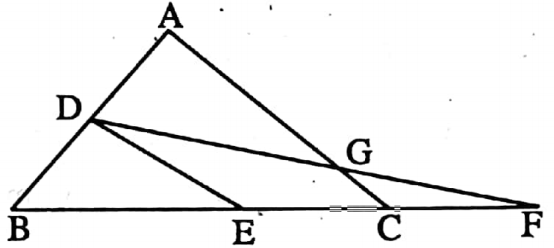
∴ DE || AC and DE = \(\frac{1}{2}\) AC
= (\(\frac{1}{2}\)x 8) cm = 4 cm
⇒ In ΔDEF, C is the mid point of EF and GC || DE [DE || AC]
⇒ In CG = \(\frac{1}{2}\) DE = (\(\frac{1}{2}\) x 4) cm = 2 cm.
∴ The length of CG is 2 cm.
Example 8. The area of a square is x2 sq. cm. Find the perimeter of the quadrilateral formed by joining midpoints of consecutive sides of that square.
Solution: Let, P, Q, R and S are the midpoints of the sides AB, BC, CD, and DA respectively of a square ABCD.
I join P, Q; Q, R; R, S; S, P; A, C and B, D.
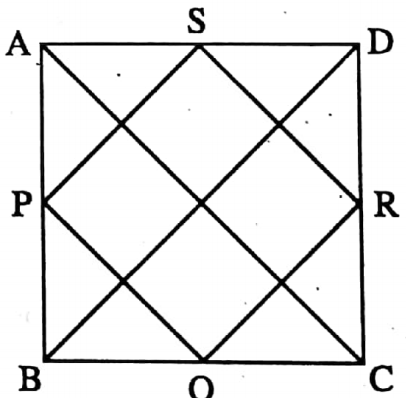
⇒ Area of the square ABCD is x2 sq. cm.
∴ The length of each side is √x2 cm or x cm and length of the each diagonal is √2x cm.
∴ AB = BC = CD = DA = x cm and AC = BD = √2x cm
⇒ In ΔABD, P and S are the midpoints of side AB and AD respectively.
⇒ PS || BD and PS = \(\frac{1}{2}\) BD \(\frac{\sqrt{2} x}{2}\) cm
∴ In the quadrilateral PQRS, PS || QR and PS = QR
∴ PQRS is a parallelogram.
⇒ In ΔABC, P and Q are the midpoints of AB and BC respectively
∴ PQ = \(\frac{1}{2}\) AC = \(\frac{\sqrt{2} x}{2}\) cm
∴ PQ = QR = \(\frac{\sqrt{2} x}{2}\) cm
⇒ In ΔBPQ, BP = BQ and ∠PBQ = 90°
∴ ∠BPQ = ∠BQP = \(\frac{180^{\circ}-90^{\circ}}{2}=45^{\circ}\)
⇒ Similarly, ∠APS = 45°
∴ ∠SPQ = 180° – ∠APS – ∠BPQ
= 180° – 45° – 45° = 90°.
⇒ Similarly, ∠PQR = 90°
⇒ As, in parallelogram PQRS, PQ = QR and ∠PQR = 90°
∴ PQRS is a square whose length of each sides is \(\frac{\sqrt{2} x}{2}\) cm
∴ Perimeter = (4 x \(\frac{\sqrt{2} x}{2}\)) cm = 2√2x cm.
∴ The perimeter of the quadrilateral form by joining midpoints of consecutive sides of that square is 2√2x cm.
Example 9. In the ΔABC, D, E, and F are midpoints of sides AB, BC, and CA respectively. In the ΔDEF, P, Q, and R are the midpoints of the sides DE, EF, and FD respectively. If PR = 3 cm then the length of AB.
Solution: In the ΔDEF, P and Q are midpoints of DE and DF respectively.
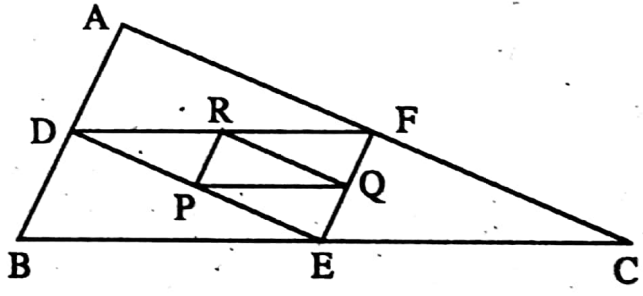
∴ PR = \(\frac{1}{2}\) EF
⇒ In the ΔABC, E and F are midpoints of BC and AC
∴ EF = \(\frac{1}{2}\) AB
⇒ or, AB = 2 EF = 2 x 2PR (4 x 3) cm = 12 cm.
∴ The length of AB is 12 cm.
Example 10. In the ΔABC, AB = x cm, BC = y cm, and ∠ABC = 90°. If D and E are midpoints of AB and BC, then find the perimeter of ΔBDE.
Solution: BD = \(\frac{1}{2}\) AB = \(\frac{x}{2}\) and BE = \(\frac{1}{2}\) BC = \(\frac{y}{2}\) cm
⇒ In ΔABC, ∠ABC = 90°
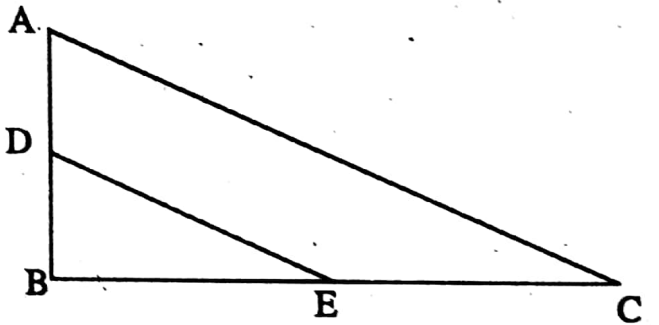
∴ AB2 + BC2 = AC2 [By Pythagorus theorem]
⇒ AC = \(\sqrt{A B^2+B C^2}\)
= \(\sqrt{x^2+y^2} \mathrm{~cm}\)
⇒ In ΔABC, D, and E are the midpoints of AB and BC
∴ DE = \(\frac{1}{2}\) AC = \(\frac{\sqrt{x^2+y^2}}{2}\) cm
⇒ Perimeter of ΔBDE = BD + BE + DE
= \(\left(\frac{x}{2}+\frac{y}{2}+\frac{\sqrt{x^2+y^2}}{2}\right)\) cm
The perimeter of ΔBDE = \(\left(\frac{x}{2}+\frac{y}{2}+\frac{\sqrt{x^2+y^2}}{2}\right)\) cm
