Geometry Chapter 3 Theorems On Area
Theorem:
- The area of parallelograms which stand on same base and between same parallels are equal.
- When a triangle and any parallelogram are on the same base and between the same parallels, the area of a triangle is half the area of the parallelogram.
- The area of triangular regions being on the same base and between same parallels is equal.
- Triangular regions of equal area standing on same base and being on the same side of it, they will be between the same parallels.
Geometry Chapter 3 Theorems On Area True Or False
Example 1. The heights of each parallelogram between the same parallel lines are same.
Solution: The perpendicular distance between two parallel lines are same.
⇒ The parallelogram ABCD and parallelogram PQRS are between the same parallels.
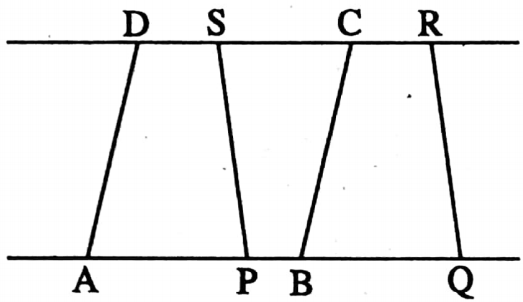
⇒ Therefore, the statement is True.
Example 2. The area of parallelogram ABCD is 32 sq. cm. O is any point on diagonal BD. If the area of ΔAOD is 5 sq. cm then the area of ΔAOP is 4 sq. cm.
Solution: I join A, C.
⇒ The diagonal AC intersects BD at point P;
⇒ So AC and BD bisects each other at point P.
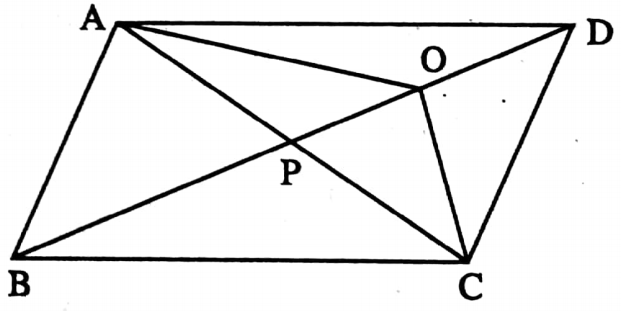
ΔADC = \(\frac{1}{2}\) parallelogram ABCD
= (\(\frac{1}{2}\) x 32) sq. cm = 16 sq. cm
⇒ DP is a median of ΔADC
∴ ΔADP = \(\frac{1}{2}\) ΔADC
= (\(\frac{1}{2}\) x 16) sq. cm = 8 sq. cm
⇒ ΔAOD = 5 sq. cm
⇒ ΔΑΟΡ = ΔADP – ΔAOD
= (8 – 5) sq. cm = 3 sq. cm
⇒ So the statement is false.
Geometry Chapter 3 Theorems On Area Fill In The Blanks
Example 1. The _______ of a triangle divides the triangular region into two equal parts of triangular regions.
Solution: median.

⇒ [ΔABD = ΔACD]
Example 2. If a triangle and a parallelogram are on the same base and between the same parallels, the ratio of areas between a parallelogram and a triangle is _______
Solution: 2 1.
⇒ ΔABC and parallelogram BCDE are on same base BC and between the same parallels.

∴ ΔABC = parallelogram BCDE
⇒ or, \(\frac{\text { parallelogram } \mathrm{BCDE}}{\triangle \mathrm{ABC}}=\frac{2}{1}\)
as, parallelogram BCDE: ΔABC= 2:1
Example 3. ΔABC and rhombus BCDE are on the same base and between the same parallels BC and FD. If ΔABC = 18 sq. cm and BC = 8 em then height of rhombus BCDE is _______
Solution: 4.5 cm.
⇒ Area of rhombus BCDE = 2 ΔABC = (2 x 18) sq.cm = 36 sq. cm
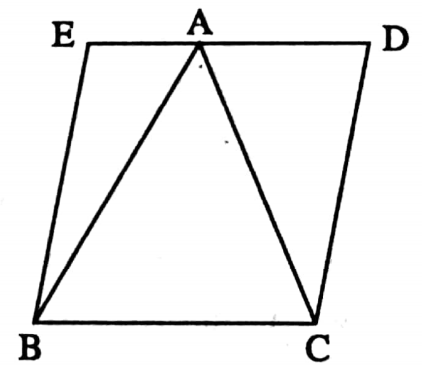
⇒ BC = 8 cm
∴ Height = \(\frac{36}{8}\) 36 cm = 4.5 cm.
Geometry Chapter 3 Theorems On Area Short Answer Type Questions
Example 1. DE is perpendicular on side AB from point D of parallelogram ABCD and BF is perpendicular on side AD from the point B ; If AB = 10 cm, AD = 8 cm, and DE 6 cm; Find the length of BF.
Solution: Area of parallelogram = base x height DE = AD × BF
⇒ Area of parallelogram ABCD = AB x DE = AD x BF
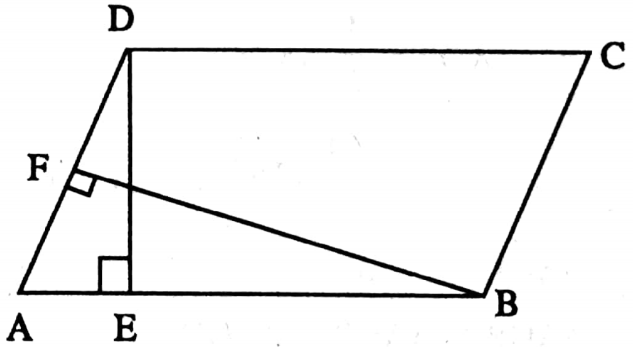
⇒ 10 cm = 6 cm = 8 cm x BF
⇒ or, BF = \(\frac{60}{8}\) cm = \(\frac{15}{2}\) = 7.5 cm
∴ The length of BF is 7.5 cm.
Example 2. The area of the parallelogram-shaped region ABCD is 100 sq. units. P is the midpoint of side BC; Find the area of triangular region ABP.
Solution: I join A and C.
⇒ AC is a diagonal of parallelogram ABCD.

∴ ΔABC = \(\frac{1}{2}\) parallelogram ABCD
= (\(\frac{1}{2}\) x 100)sq. unit = 50 sq. unit
AP is a median of ΔABC
∴ΔABP = \(\frac{1}{2}\) ΔABC = (\(\frac{1}{2}\) x 50) sq. unit
= 25 sq. unit.
∴ The area of the triangular region of ΔABP is 25 sq. unit.
Example 3. AD is the median of triangle ABC and P is any point on side AC in such a way that area of ΔADP: area of ΔABD = 2: 3. Find the area of ΔPDC: area of ΔABC.
Solution: AD is a median of ΔABC
∴ ΔABD = ΔADC = \(\frac{1}{2}\) ABC
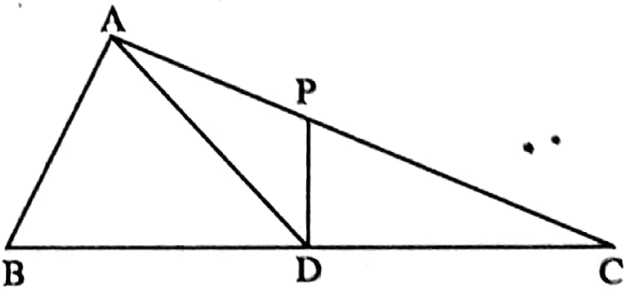
\(\frac{\triangle \mathrm{ADP}}{\triangle \mathrm{ABD}}=\frac{2}{3}\) [given]
∴ \(\frac{\Delta \mathrm{ADP}}{\Delta \mathrm{ADC}}=\frac{2}{3}\)
[ΔABD = ΔADC]
⇒ or, \(\triangle \mathrm{ADP}=\frac{2}{3} \triangle \mathrm{ADC}\)
⇒ as, \(\frac{\Delta \mathrm{PDC}}{\Delta \mathrm{ABC}}=\frac{\Delta \mathrm{ADC}-\Delta \mathrm{ADP}}{\Delta \mathrm{ABC}}\)
= \(\frac{\Delta \mathrm{ADC}-\frac{2}{3} \Delta \mathrm{ADC}}{\Delta \mathrm{ABC}}=\frac{\frac{1}{3} \Delta \mathrm{ADC}}{\Delta \mathrm{ABC}}\)
= \(\frac{\frac{1}{3} \times \frac{1}{2} \Delta \mathrm{ABC}}{\Delta \mathrm{ABC}}=\frac{1}{6}\)
∴ ΔPDC: ΔABC = 1: 6.
Example 4. BDE is a parallelogram. F is midpoint of side ED. If area of triangular region ABD is 20 sq. unit, then find the area of triangular region AEF.
Solution: AD is a diagonal of parallelogram ABDE
⇒ ΔADE = ΔABD = 20 sq. cm
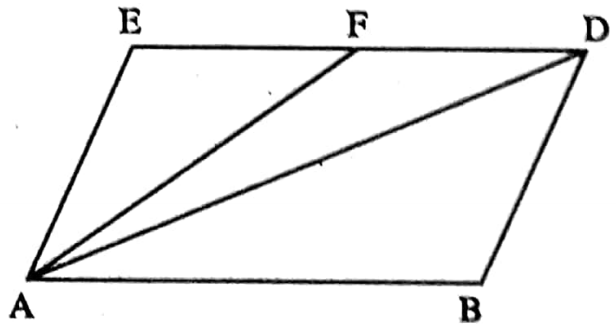
⇒ AE is an median of ΔADE
∴ ΔAEF = \(\frac{1}{2}\) ΔADE
= (\(\frac{1}{2}\) x 20) sq cm = 10 sq. cm
∴ The area of triangular is 10 sq. cm.
Example 5. PQRS is a parallelogram. X and Y are the midpoints of side PQ and SR respectively. Join diagonal SQ, Find the area of the parallelogram shaped region XQRY: area of triangular region QSR.
Solution: I join Q, Y.
⇒ In quadrilateral XQRY,

⇒ QX || RY [PQ || SR]
and QX = RY [\(\frac{1}{2}\) PQ = \(\frac{1}{2}\) SR]
∴ XQRY is a parallelogram.
⇒ QY is a diagonal of parallelogram XQRY.
∴ ΔQRY = \(\frac{1}{2}\) parallelogram XQRY
⇒ or, Parallelogram XQRY = 2 ΔQRY……..(1)
⇒ QY is a median of ΔQSR.
∴ ΔQRY = \(\frac{1}{2}\) ΔQSR
⇒ or, ΔQSR = 2 ΔQSR
⇒ or, ΔQSR = 2 ΔQRY……(2)
⇒ From (1) and (2), parallelogram XQRY = ΔQSR
∴ Parallelogram XQRY: ΔQSR = 1: 1.
Example 6. If the area of parallelogram PQRS is 15 sq. cm, then find the area of parallelogram PMNO.
Solution: I join O, Q.
⇒ ΔPOQ and parallelogram PQRS are on same base and between the same parallels.
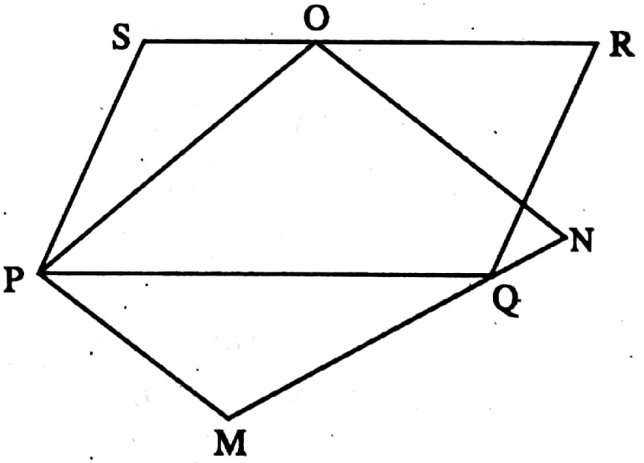
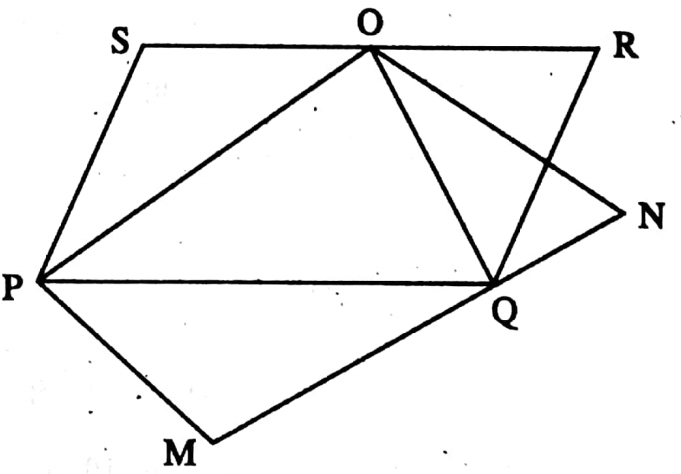
∴ ΔPOQ = \(\frac{1}{2}\) parallelogram PQRS
= (\(\frac{1}{2}\)x 15) sq. cm
= 7.5 sq. cm
⇒ Similarly, ΔPOQ = \(\frac{1}{2}\) = parallelogram PMNO
⇒ or, parallelogram PMNO = 2 ΔPOQ
= (2 x 7.5) sq. cm = 15 sq. cm
∴ The area of parallelogram PMNO is 15 sq. cm.
Example 7. In ΔABC D is the midpoint of side AB and DBCE is a parallelogram; If the area of ΔABC is 40 sq. cm, then find the area of parallelogram DBCE.
Solution: DE intersects AC at point F.
⇒ In ΔABC, D is the midpoint of AB and DE || BC;
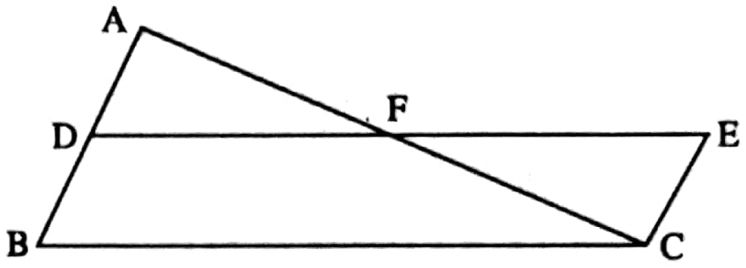
∴ F is the midpoint of AC.
In ΔADF and ΔCEF,
∠AFD = ∠CFE [vertically opposite angles]
∠DAF = alternate ∠ECF
[AB || CE and AC is intersection]
∴ AF = CF
∴ ΔADF ≅ ΔCEF [By A-A-S criterion of B congruences]
∴ ΔADF = ΔCEF
Area of parallelogram DBCE
= Area of ΔCEF + area of quadrilateral ΔCFD
= Area of ΔADF+ area of quadrilateral BCFD = Area of ΔABC= 40 sq. cm.
∴ The area of parallelogram DBCE is 40 sq. cm.
Example 8. In trapezium, ABCD, AD || BC, and P and Q are midpoints of side AB and DC 18 em then find the ratio of area of quadrilateral APQD respectively. If AD = 12 cm and BC and area of quadrilateral PBCQ.
Solution: P and Q are the midpoints of side AB and DC respectively.
∴ PQ || AD || BC
and PQ = \(\frac{1}{2}\) (AD + BC) = \(\frac{1}{2}\) (12 + 18) cm = 12 cm
AS, AD || PQ ∴ APQD is a trapezium
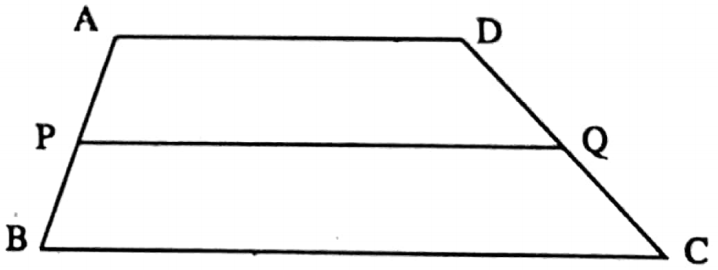
Similarly, PBCQ is a trapezium
As P and Q are midpoints of side AB and DC respectively
∴ Height of trapezium APQD and PBCQ are same.
Let, this height be h cm.
∴ Area of trapezium APQD = \(\frac{1}{2}\) (AD + PQ) x h
= \(\frac{1}{2}\) (12 + 15) x h sq. cm = \(\frac{27h}{2}\) sq. cm.
Area of trapezium PBCQ = \(\frac{1}{2}\) (PQ + BC) x h
= \(\frac{1}{2}\) (15 + 18) x h sq. cm. = \(\frac{33h}{2}\) sq. cm
∴ Ratio of areas between two trapezium is \(\frac{27h}{2}\): \(\frac{33h}{2}\)
= \(\frac{27h}{2}\): \(\frac{33h}{2}\) = 9: 11
∴ The ratio of area of quadrilateral APQD and area of quadrilateral PBCQ is 9: 11.
Example 9. In ΔABC, D and E are midpoints of side AB and BC respectively; F is the midpoint of side AD. If the area of ΔABC is 24 sq. cm then find the area of ΔCEF.
Solution: I join C, D. CD is a median of ΔABC
∴ ΔADC = \(\frac{1}{2}\) ΔABC

Again, CF is a median of ΔADC
∴ ΔACF = \(\frac{1}{2}\) ΔADC
= \(\frac{1}{2}\) x \(\frac{1}{2}\) ΔABC = \(\frac{1}{2}\) ΔABC
FE is a median of ΔFBC
∴ ΔCEF = \(\frac{1}{4}\) ΔFBC
= \(\frac{1}{2}\) (ΔABC – ΔACF)
= \(\frac{1}{2}\) (ΔABC – \(\frac{1}{4}\) ΔABC)
= \(\frac{1}{2}\) x \(\frac{3}{4}\) ΔABC
= (\(\frac{3}{8}\) x 24) sq. cm = 9 sq. cm
∴ The area of ACEF is 9 sq. cm.
Example 10. In parallelogram ABCD, the points P and Q on sides AB and DC such that BP = 2AP and DQ = 2CQ; If the area of parallelogram ABCD is 36 sq. cm then find the area of quadrilateral APCQ.
Solution: BP = 2AP
as, AB – AP = 2AP
or, AB = 3AP
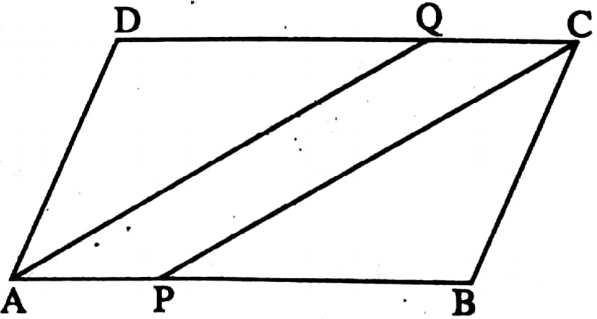
or, AP = \(\frac{1}{3}\) AB
Similarly, CQ = \(\frac{1}{3}\) DC
Again AB = DC
∴ 3AP = 3CQ
or, AP = CQ
In quadrilateral APCQ, AP = CQ and AP || CQ
∴ APCQ is a parallelogram
As parallelogram APCQ and parallelogram ABCD are between the same parallels AB and DC
∴ Their heights are same. Let height is h cm
∴ Area of parallelogram ABCQ = AP x h
= \(\frac{1}{3}\) AB x h = \(\frac{1}{3}\) x area of parallelogram ABCD
= (\(\frac{1}{3}\) x 36) sq. cm = 12 sq. cm
∴ The area of quadrilateral APCQ is 12 sq. cm.
