Algebra Chapter 6 Simplification Of Algebraic Expression
When we are dividing the numerator and denominator by common factor we get the reduced form:
Example: \(\frac{15 a^2 b^3 c^4}{18 a^3 b^2 c^5}=\frac{15 a^2 b^3 c^4 \div 3 a^2 b^2 c^4}{18 a^3 b^2 c^5 \div 3 a^2 b^2 c^4}\)
[Common factor of Numerator and denominator is 3a2b2c4]
= \(\frac{5b}{6ac}\)
Alternate method:
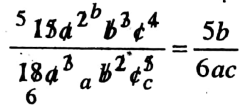

Algebra Chapter 6 Simplification Of Algebraic Expression Examples
Example 1. Express the following algebraic fractions in the reduced form:
Read and Learn More WBBSE Solutions For Class 8 Maths
1. \(\frac{21 x^4 y z^3}{49 x^2 y^6 z^2}\)
Solution: \(\frac{21 x^4 y z^3}{49 x^2 y^6 z^2}\) = \(\frac{3 x^2 z}{7 y^5}\)
2. \(\frac{x^2-6 x+5}{x^2-1}\)
Solution: \(\frac{x^2-6 x+5}{x^2-1}=\frac{x^2-(5+1) x+5}{x^2-1}=\frac{x^2-5 x-x+5}{x^2-1}\)
= \(\frac{x(x-5)-1(x-5)}{(x+1)(x-1)}=\frac{(x-5)(x-1)}{(x+1)(x-1)}=\frac{x-5}{x+1}\)
⇒ \(\frac{x^2-6 x+5}{x^2-1}\) = \(\frac{x(x-5)-1(x-5)}{(x+1)(x-1)}=\frac{(x-5)(x-1)}{(x+1)(x-1)}=\frac{x-5}{x+1}\)
| WBBSE Class 8 English Functional Grammar | WBBSE Class 8 English Reading Skills |
| WBBSE Solutions For Class 8 English | WBBSE Solutions For Class 8 Maths |
3. \(\frac{a^3-b^3}{a^2-b^2}\)
Solution: \(\frac{a^3-b^3}{a^2-b^2}=\frac{(a-b)\left(a^2+a b+b^2\right)}{(a+b)(a-b)}=\frac{a^2+a b+b^2}{a+b}\)
4. \(\frac{2 a^2+a b-b^2}{a^3+a^2 b-a-b}\)
Solution: \(\frac{2 a^2+a b-b^2}{a^3+a^2 b-a-b}=\frac{2 a^2+(2-1) a b-b^2}{a^2(a+b)-1(a+b)}=\frac{2 a^2+2 a b-a b-b^2}{(a+b)\left(a^2-1\right)}\)
= \(\frac{2 a(a+b)-b(a+b)}{(a+b)\left(a^2-1\right)}=\frac{(a+b)(2 a-b)}{(a+b)(a+1)(a-1)}=\frac{2 a-b}{(a+1)(a-1)}\)
5. \(\frac{x^2-y^2-2 x z+z^2}{x^2+y^2-z^2+2 x y}\)
Solution: \(\frac{x^2-y^2-2 x z+z^2}{x^2+y^2-z^2+2 x y}\)
= \(\frac{\left(x^2-2 x z+z^2\right)-y^2}{\left(x^2+2 x y+y^2\right)-z^2}=\frac{(x-z)^2-y^2}{(x+y)^2-z^2}=\frac{(x-z+y)(x-z-y)}{(x+y+z)(x+y-z)}\)
= \(\frac{(x+y-z)(x-y-z)}{(x+y+z)(x+y-z)}=\frac{x-y-z}{x+y+z}\)
6. \(\frac{a^2-2 a b-15 b^2}{a^2-9 a b+20 b^2}\)
Solution: \(\frac{a^2-2 a b-15 b^2}{a^2-9 a b+20 b^2}\)
= \(\frac{a^2-(5-3) a b-15 b^2}{a^2-(5+4) a b+20 b^2}=\frac{a^2-5 a b+3 a b-15 b^2}{a^2-5 a b-4 a b+20 b^2}\)
= \(\frac{a(a-5 b)+3 b(a-5 b)}{a(a-5 b)-4 b(a-5 b)}=\frac{(a-5 b)(a+3 b)}{(a-5 b)(a-4 b)}=\frac{a+3 b}{a-4 b}\)
Example 2. Convert the fraction into same denominator.
1.\(\frac{a}{b c}+\frac{b}{c a}-\frac{c}{a b}\)
Solution: \(\frac{a}{b c}+\frac{b}{c a}-\frac{c}{a b}\)
f(x) = \(\frac{a \times a}{a \times b c}+\frac{b \times b}{c a \times b}-\frac{c \times c}{a b \times c}\)
[LCM of bc, ca and ab is abc]
f(x) = \(\frac{a^2}{a b c}+\frac{b^2}{a b c}-\frac{c^2}{a b c}=\frac{a^2+b^2-c^2}{a b c}\)
2. \(\frac{p}{(a-b)(b-c)}+\frac{q}{(b-c)(c-a)}+\frac{r}{(c-a)(a-b)}\)
Solution: \(\frac{p}{(a-b)(b-c)}+\frac{q}{(b-c)(c-a)}+\frac{r}{(c-a)(a-b)}\)
f(a) = \(\frac{p(c-a)}{(a-b)(b-c)(c-a)}+\frac{q(a-b)}{(a-b)(b-c)(c-a)}+\frac{r(b-c)}{(c-a)(a-b)(b-c)}\)
f(a) = \(\frac{p(c-a)+q(a-b)+r(b-c)}{(a-b)(b-c)(c-a)}\)
Example 3. Simplify \(\left(\frac{8}{x}+\frac{x}{4}-3\right)+\left(\frac{x}{12}-\frac{1}{3}-\frac{8}{3 x}\right)\)
Solution: f(x) = \(\left(\frac{8}{x}+\frac{x}{4}-3\right)+\left(\frac{x}{12}-\frac{1}{3}-\frac{8}{3 x}\right)=\left(\frac{32+x^2-12 x}{4 x}\right)+\left(\frac{x^2-4 x-32}{12 x}\right)\)
f(x) = \(\frac{\left(x^2-12 x+32\right)}{4 x} \times \frac{12 x^3}{x^2-4 x-32}=\frac{x^2-(8+4) x+32}{1} \times \frac{3}{x^2-(8-4) x-32}\)
f(x) = \(\frac{x^2-8 x-4 x+32}{1} \times \frac{3}{x^2-8 x+4 x-32} \times \frac{3}{x(x-8)+4(x-8)}\)
f(x) = \(\frac{x(x-8)-4(x-8)}{1} \times \frac{3(x-4)}{x+4}\)
Example 4. Simplify: \(\frac{x-1}{x-2}-\frac{4}{4-x^2}+\frac{2}{2-x}-\frac{x+1}{x+2}\)
Solution: f(x) = \(\frac{x-1}{x-2}-\frac{4}{4-x^2}+\frac{2}{2-x}-\frac{x+1}{x+2}\)
f(x) = \(\frac{x-1}{x-2}-\frac{4}{-\left(x^2-4\right)}+\frac{2}{-(x-2)}-\frac{x+1}{x+2}\)
f(x) = \(\frac{x-1}{x-2}+\frac{4}{(x+2)(x-2)}-\frac{2}{x-2}-\frac{x+1}{x+2}\)
f(x) = \(\frac{(x-1)(x+2)+4-2(x+2)-(x+1)(x-2)}{(x-2)(x+2)}\)
f(x) = \(\frac{x^2+2 x-x-2+4-2 x-4-x^2+2 x-x+2}{(x-2)(x+2)}\)
f(x) = \(\frac{2 x-2 x}{(x-2)(x+2)}=\frac{0}{(x-2)(x+2)}=0\)
Example 5. \(\frac{1}{a-1}+\frac{1}{a+1}+\frac{2 a}{a^2+1}+\frac{4 a^3}{a^4+1}+\frac{8 a^7}{a^8+1}\)
Solution: f(a) = \(\frac{1}{a-1}+\frac{1}{a+1}+\frac{2 a}{a^2+1}+\frac{4 a^3}{a^4+1}+\frac{8 a^7}{a^8+1}\)
f(a) = \(\frac{a+1+a-1}{(a-1)(a+1)}+\frac{2 a}{a^2+1}+\frac{4 a^3}{a^4+1}+\frac{8 a^7}{a^8+1}\)
f(a) = \(\frac{2 a}{a^2-1}+\frac{2 a}{a^2+1}+\frac{4 a^3}{a^4+1}+\frac{8 a^7}{a^8+1}\)
f(a) = \(\frac{2 a\left(a^2+1\right)+2 a\left(a^2-1\right)}{\left(a^2-1\right)\left(a^2+1\right)}+\frac{4 a^3}{a^4+1}+\frac{8 a^7}{a^8+1}\)
f(a) = \(\frac{2 a^3+2 a+2 a^3-2 a}{a^4-1}+\frac{4 a^3}{a^4+1}+\frac{8 a^7}{a^8+1}\)
f(a) = \(\frac{4 a^3}{a^4-1}+\frac{4 a^3}{a^4+1}+\frac{8 a^7}{a^8+1}=\frac{4 a^3\left(a^4+1\right)+4 a^3\left(a^4-1\right)}{\left(a^4-1\right)\left(a^4+1\right)}+\frac{8 a^7}{a^8+1}\)
f(a) = \(\frac{4 a^7+4 a^8+4 a^7-4 a^3}{a^8-1}+\frac{8 a^7}{a^8+1}=\frac{8 a^7}{a^8-1}+\frac{8 a^7}{a^8+1}\)
f(a) = \(\frac{8 a^7\left(a^8+1\right)+8 a^7\left(a^8-1\right)}{\left(a^8-1\right)\left(a^8+1\right)}=\frac{8 a^{15}+8 a^7+8 a^{15}-8 a^7}{a^{16}-1}=\frac{16 a^{15}}{a^{16}-1}\)
Example 6. Simplify: \(\frac{y+z-x}{(x-y)(x-z)}+\frac{z+x-y}{(y-x)(y-z)}+\frac{x+y-z}{(z-x)(z-y)}\)
Solution: f(x) = \(\frac{y+z-x}{(x-y)(x-z)}+\frac{z+x-y}{(y-x)(y-z)}+\frac{x+y-z}{(z-x)(z-y)}\)
f(x) = \(\frac{y+z-x}{-(x-y)(z-x)}+\frac{z+x-y}{-(x-y)(y-z)}+\frac{x+y-z}{-(z-x)(y-z)}\)
f(x) = \(-\left[\frac{y+z-x}{(x-y)(z-x)}+\frac{z+x-y}{(x-y)(y-z)}+\frac{x+y-z}{(z-x)(y-z)}\right]\)
f(x) = \(-\left[\frac{(y-z)(y+z-x)+(z-x)(z+x-y)+(x-y)(x+y-z)}{(x-y)(y-z)(z-x)}\right]\)
f(x) = \(-\left[\frac{y^2-z^2-x y+x z+z^2-x^2-y z+x y+x^2-y^2-x z+y z}{(x-y)(y-z)(z-x)}\right]\)
f(x) = \(-\left[\frac{0}{(x-y)(y-z)(z-x)}\right]=0\)
Example 7. Simplify: \(\frac{y+z}{y z}(y+z-x)+\frac{z+x}{z x}(z+x-y)+\frac{x+y}{x y}(x+y-z)\)
Solution: f(x) = \(\frac{y+z}{y z}(y+z-x)+\frac{z+x}{z x}(z+x-y)+\frac{x+y}{x y}(x+y-z)\)
f(x) = \(\left(\frac{1}{z}+\frac{1}{y}\right)(y+z-x)+\left(\frac{1}{x}+\frac{1}{z}\right)(z+x-y)+\left(\frac{1}{y}+\frac{1}{x}\right)(x+y-z) \)
f(x) = \(\frac{1}{z}(y+z-x)+\frac{1}{y}(y+z-x)+\frac{1}{x}(z+x-y)+\frac{1}{z}(z+x-y)+\frac{1}{y}(x+y-z)+\frac{1}{x}(x+y-z)\)
f(x) = \(\frac{y}{z}+1-\frac{x}{z}+1+\frac{z}{y}-\frac{x}{y}+\frac{z}{x}+1-\frac{y}{x}+1+\frac{x}{z}-\frac{y}{z}+\frac{x}{y}+1-\frac{z}{y}+1+\frac{y}{x}-\frac{z}{x}=6\)
Example 8. Simplify: \(\frac{1-2 a+a^2}{1-a^6} \div \frac{1-3 a+3 a^2-a^3}{1+a^2+a^4} \times \frac{(1-a)^2}{1+a}\)
Solution: f(a) = \(\frac{1-2 a+a^2}{1-a^6} \div \frac{1-3 a+3 a^2-a^3}{1+a^2+a^4} \times \frac{(1-a)^2}{1+a}\)
f(a) = \(\frac{(1-a)^2}{(1)^3-\left(a^3\right)^2} \div \frac{(1)^3-31^2 \cdot a+3 \cdot 1 \cdot a^2-a^3}{(1)^2+2 \cdot 1 \cdot a^2+\left(a^2\right)^2-a^2} \times \frac{(1-a)^2}{1+a}\)
f(a) = \(\frac{(1-a)^2}{\left(1+a^3\right)\left(1-a^3\right)} \div \frac{(1-a)^3}{\left(1+a^2\right)^2-a^2} \times \frac{(1-a)^2}{1+a}\)
f(a) = \(\frac{(1-a)^2}{(1+a)\left(1-a+a^2\right)(1-a)\left(1+a+a^2\right)} \div \frac{(1-a)^3}{\left(1+a^2+a\right)\left(1+a^2-a\right)} \times \frac{(1-a)^2}{1+a}\)
f(a) = \(\frac{(1-k)(1-k)}{(1+a)\left(1-a+a^2\right)(1-a)\left(1+a+a^2\right)} \times \frac{\left(1+\alpha+a^2\right)\left(1-k+d^2\right)}{(1-k)(1-k)(1-k)} \times \frac{(1-k)(1-k)}{(1+a)}\)
f(a) = \(\frac{1}{(1+a)^2}=\frac{1}{1+2 a+a^2}\)
Example 9. Simplify: \(\frac{2-\frac{7}{a+3}}{1-\frac{5}{a+3}} \times \frac{1-\frac{1}{a-1}}{1+\frac{1}{2(a-1)}}\)
Solution: f(a) = \(2-\frac{\frac{7}{a+3}}{1-\frac{5}{a+3}} \times \frac{1-\frac{1}{a-1}}{1+\frac{1}{2(a-1)}}=\frac{\frac{2 a+6-7}{a+3}}{\frac{a+3-5}{a+3}} \times \frac{\frac{a-1-1}{a-1}}{\frac{2 a-2+1}{2(a-1)}}\)
f(a) = \(\frac{(2 a-1)}{(a+3)} \times \frac{(a+3)}{(a-2)} \times \frac{(a-2)}{(a-1)} \times \frac{2(a-1)}{(2 a-1)}=2\)
Example 10. If ab + bc + ca = 0, then prove that \(\frac{1}{a^2-b c}+\frac{1}{b^2-c a}+\frac{1}{c^2-a b}=0\)
Solution: f(a) = \(\frac{1}{a^2-b c}+\frac{1}{b^2-c a}+\frac{1}{c^2-a b}\)
f(a) = \(\frac{1}{a^2+a b+a c}+\frac{1}{b^2+a b+b c}+\frac{1}{c^2+b c+c a}\) [because ab+bc+ca=0]
f(a) = \(\frac{1}{a(a+b+c)}+\frac{1}{b(b+a+c)}+\frac{1}{c(c+b+a)}=\frac{b c+a c+a b}{a b c(a+b+c)}\)
f(a) = \(\frac{0}{a b c(a+b+c)}=0\)
Example 11. Choose the correct answer:
1. The simplify form of \(\frac{10 p^3 x^2}{15 p^3 x}\)
- \(\frac{2p}{3x}\)
- \(\frac{5p}{3x}\)
- \(\frac{3x}{2p}\)
- \(\frac{2x}{3}\)
Solution:
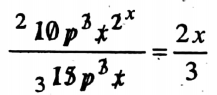
∴ So the correct answer 4. \(\frac{2x}{3}\)
2. \(\frac{5 p^2+30 p}{p^2+2 p-24}\)=?
- \(\frac{p+5}{p+4}\)
- p + 2
- \(\frac{5p}{p-4}\)
- \(\frac{6p}{p-5}\)
Solution: \(\frac{5 p^2+30 p}{p^2+2 p-24}=\frac{5 p(p+6)}{(p+6)(p-4)}=\frac{5 p}{p-4}\)
∴ So the correct answer is 3. \(\frac{5p}{p-4}\)
3. \(\frac{b^2-c^2}{b+c}+\frac{c^2-a^2}{c+a}+\frac{a^2-b^2}{a+b}=?\)
- 0
- 1
- -1
- 2
Solution: \(\frac{b^2-c^2}{b+c}+\frac{c^2-a^2}{c+a}+\frac{a^2-b^2}{a+b}\)
= \(\frac{(b+c)(b-c)}{(b+c)}+\frac{(c+a)(c-a)}{(c+a)}+\frac{(a+b)(a-b)}{(a+b)}\)
= b – c + c – a + a – b = 0
Example 12. Write ‘True’ or ‘False’
1. \(\frac{x^2+y^2}{x-y}=x+y\)
Solution: The statement is false
2. \(\frac{1}{x-2}-\frac{4}{x^2-4}=\frac{1}{x+2}\)
Solution: \(\frac{1}{x-2}-\frac{4}{x^2-4}\)
= \(\frac{1}{x-2}-\frac{4}{(x+2)(x-2)}\)
= \(\frac{x+2-4}{(x+2)(x-2)}=\frac{(x-2)}{(x+2)(x-2)}=\frac{1}{x+2}\)
The statement is true.
3. \(\frac{m^2+3 m}{m^2+4 m+3}+\frac{m^2-9}{m^2-2 m-3}=\frac{m}{m+3}\)
Solution: \(\frac{m^2+3 m}{m^2+4 m+3}+\frac{m^2-9}{m^2-2 m-3}\)
= \(\frac{m(n+3)}{(m+3)(m+1)}+\frac{(m+3)(m-3)}{(m-3)(m+1)}\)
= \(\frac{m}{m+1}+\frac{m+3}{m+1}=\frac{m+m+3}{m+1}=\frac{2 m+3}{m+1}\)
The statement is false
Example 13. Fill in the blanks
1. \(\frac{(a+b)^2-(a-b)^2}{4 ab}\) = _________
Solution: \(\frac{(a+b)^2-(a-b)^2}{4 a b}=\frac{4 a b}{4 a b}=1\)
\(\frac{(a+b)^2-(a-b)^2}{4 ab}\) = \(\frac{(a+b)^2-(a-b)^2}{4 a b}=\frac{4 a b}{4 a b}=1\)
2. \(\frac{3 a^2-9 a b}{a^2-3 a b}\) = _________
Solution: \(\frac{3 a^2-9 a b}{a^2-3 a b}=\frac{3 d(a-3 b)}{d(a-3 b)}=3\)
\(\frac{3 a^2-9 a b}{a^2-3 a b}\) = \(\frac{3 a^2-9 a b}{a^2-3 a b}=\frac{3 d(a-3 b)}{d(a-3 b)}=3\)
3. \(\frac{a}{b}+\frac{b}{a}-\frac{a^2+b^2}{a b}\) = _________
Solution: \(\frac{a}{b}+\frac{b}{a}-\frac{a^2+b^2}{a b}=\frac{a^2+b^2-a^2-b^2}{a b}=\frac{0}{a b}=0\).
\(\frac{a}{b}+\frac{b}{a}-\frac{a^2+b^2}{a b}\) = \(\frac{a}{b}+\frac{b}{a}-\frac{a^2+b^2}{a b}=\frac{a^2+b^2-a^2-b^2}{a b}=\frac{0}{a b}=0\).
