WBBSE Solutions For Class 7 Maths Geometry Chapter 5 Concept Of Congruency
Question 1. what is congruency?
Solution:
Congruency is the property of two geometrical Figures if one of them can be made to coincide with the other by means of reflection, transformation, translation, or rotation of their combination.
If the two Geometrical Figures are of the same shape and size they are said to be congruent to each other.
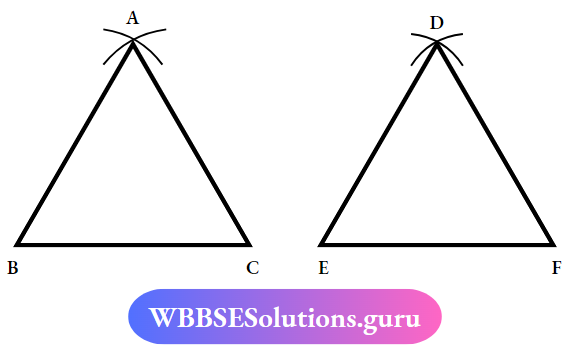
In two triangles ABC and DEF, IF AB = DE, BC= EF, CA= DF
∠A = ∠A, ∠B = ∠E, ∠C = ∠F
∴ ΔABC ≅ ΔDEF
Question 2. Write the condition of the congruence of a triangle.
Solution:
Congruence of triangle
Two triangles are said to be congruent if their respective side angles are equal and when they are placed upon one another cover each other completely.

In two triangles ABC, DEF.
Condition:
IF AB=DE, BC= EF, CA= FD, and
∠A = ∠D, ∠B = ∠E, ∠C = ∠F
∴ ΔABC ≅ ΔDEF
Question 3. What is SSS congruency of a triangle? SSS (Side-Side – Side)
Solution:
If the lengths of three sides of a triangle are equal to the lengths of three sides of the other triangle then the triangles are congruent.
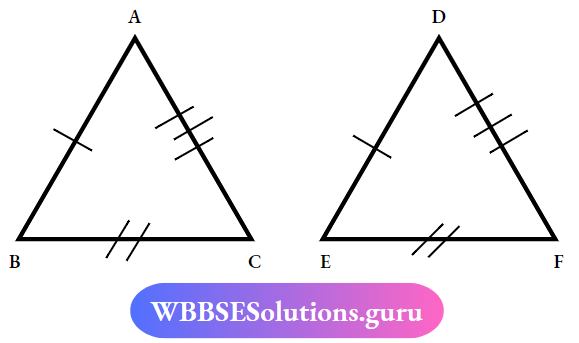
In ΔABC and ΔDEF
AB= DE, BC= EF and AC = DF
∴ ΔAB C ≅ ΔDEF
Question 4. what is the SAS congruency of a triangle SAS (Side- Angle- side)
Solution:
Two triangles are congruent if the length of two sides and the measurement of the included angle of one triangle are equal to the length of two sides and the measurement of the included angle of the other triangle
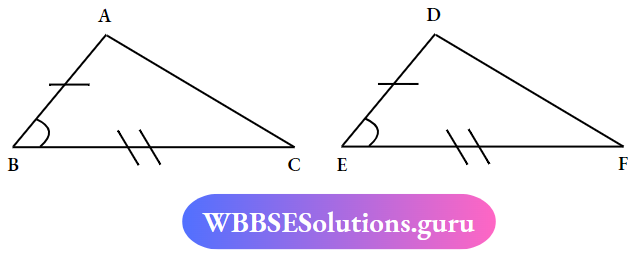
In ΔABC and ΔDEF
AB = DE, ∠ABC = ∠DEF and BC= EF
∴ ΔABC ≅ ΔDEF
Question 5. What is AAS congruency of a triangle AAS (Angle- Angle-side)
Solution:
Two triangles are congruent if the measurement of any Pair of angles and length of one pair of corresponding Sides are equal to other triangle.
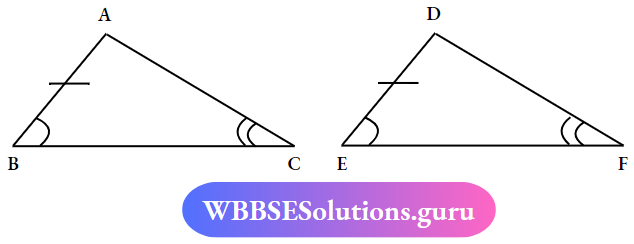
In ΔABC and ΔDEF
∠B= ∠E, ∠C = ∠F and AB = DE
∴ ΔABC ≅ ΔDEF.
Question 6. What is RHS congruency of a triangle? RHS (Right Angle- Hypotenuse – Side)
Solution:
If in two right-angled triangles, the length of the hypotenuse and the length of one triangle is equal to the length of the hypotenuse and the length of one side of the other triangle, then the two triangles are congruent.
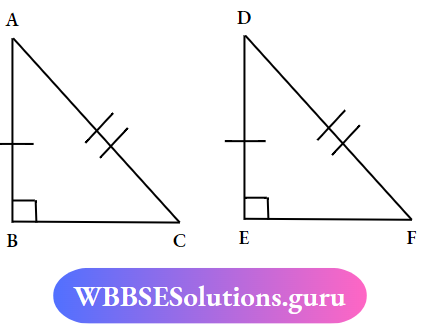
In ΔABC and ΔDEF
∠ABC ≈ ∠DEF = 90°
Hypotenuse AC = Hypotenuse DF and AB = DE
∴ ΔABC ≅ ΔDEF
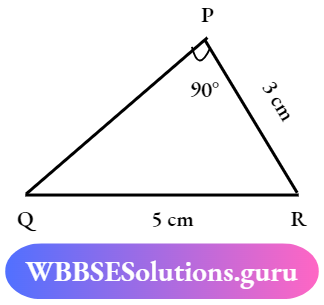
Question 7. Find out whether the triangles are congruent
Solution:
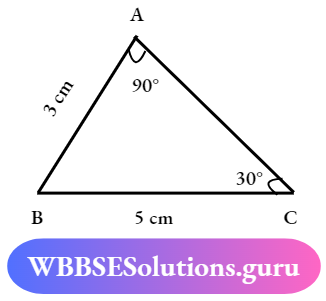
AB = PQ, ∠A = ∠P
BC = QR, ∠B = ∠Q
CA = PR, ∠C = ∠R
Then the triangles are incongruent
Here,
AB ≠ PQ, ∠A = ∠P
BC = QR, ∠Q ≠ ∠B
CA ≠ PR, ∠C ≠ ∠R
∴ The triangles are non- congruent.
2.
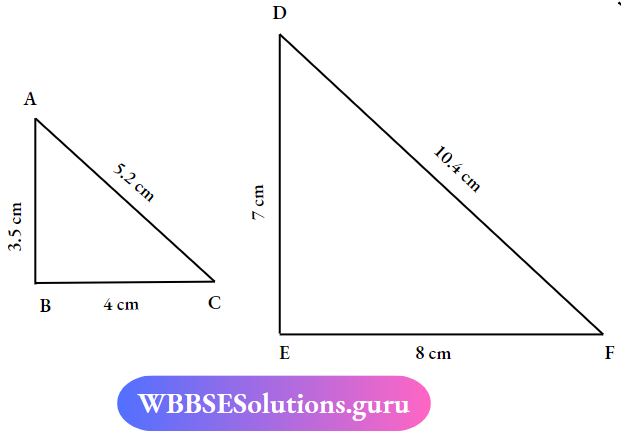
Here,
AB ≠ DE
BC ≠ EF
CA ≠ DF
∴ The ΔABC and ΔDEF are not congruent.
3.
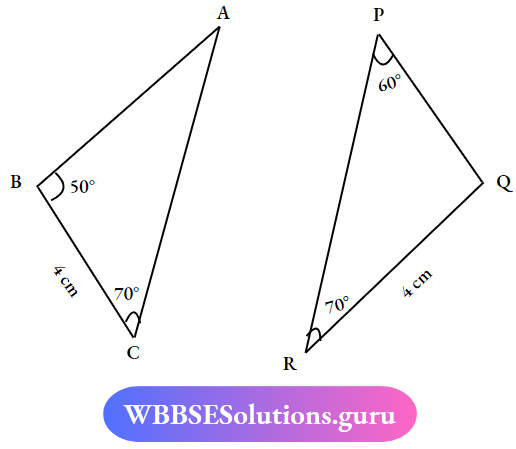
Let us Name the triangles First
BC = QR, ∠C = ∠R
∠B = ∠Q Sum of angles in a Δle is 180.
∠P = ∠A
According to the AAS Condition, the two triangles are in Congruence.
4.

In ΔABC and ΔDEF
∠ABC = ∠DEF = 90°
Hypotenuse AC = DF and AB = DE,
∴ ΔABC ≅ ΔDEF
5.
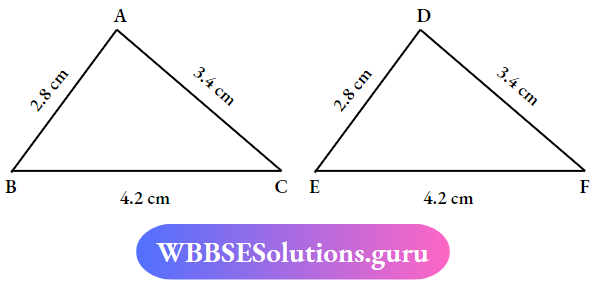
According to SSS Congruent
AB = DE
BC = EF
AC = FD
∴ ΔABC ≅ ΔDEF
6.
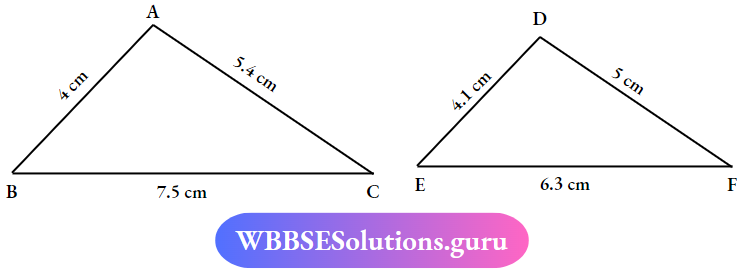
Let us Name the triangles First ΔABC, ΔDEF
Given the sides of Δle
AB ≠ DE
BC ≠ EF
AC ≠ FD
∴ The ΔABC and ΔDEF are non-congruent.
