WBBSE Class 9 Maths Geometry Chapter 1 Properties Of Parallelogram Multiple Choice Questions

WBBSE Class 9 Maths  Geometry Chapter 1 Properties Of Parallelogram Multiple Choice Questions

Example 1. In the parallelogram ABCD, ∠BAD = 75° and ∠CBD = 60°, then the value of ∠BDC is

1. 60°
2. 75°
3. 45°
4. 50°

Solution: The correct answer is 3. 45°

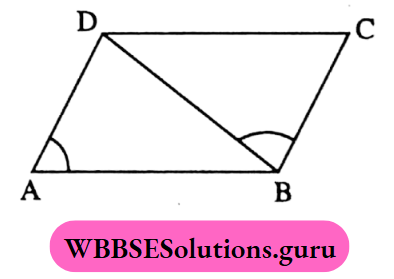
⇒ In the parallelogram ABCD, ∠C = ∠A = 75°

⇒ In ΔBCD, ∠BDC+ ∠CBD + ∠C = 180°

⇒ ∠BDC +60° + 75° = 180°

⇒ or, ∠BDC = 180° – (60° + 75°) = 45°

The value of ∠BDC is 45°

Read and Learn More WBBSE Class 9 Maths Multiple Choice Questions

Example 2. Which of the following geometric diagonals equal in length

1. Parallelogram
2. Rhombus
3. Trapezium
4. Rectangle

Solution: The correct answer is 4. Rectangle

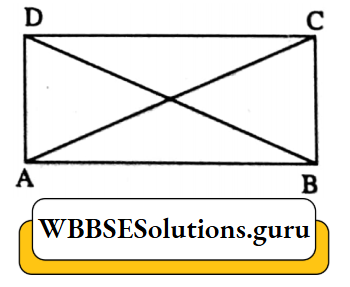
⇒ The diagonals of each rectangle are equal in length.

Example 3. In the parallelogram ABCD, ∠BAD = ∠ABC, the parallelogram ABCD is a

1. Rhombus
2. Trapezium
3. Rectangle
4. None of them

Solution: The correct answer is 3. Rectangle

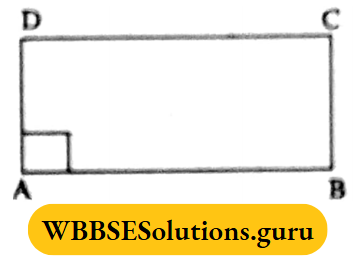
⇒ In a parallelogram, ABCD, AD || BC, and AB is the intersection

∴ ∠BAD + ∠ABC = 180°

⇒ ∠BAD + ∠BAD = 180°

2 ∠BAD = 180°

⇒ ∠BAD = 90°

∴ Parallelogram ABCD is a rectangle

Example 4. In the parallelogram ABCD, M is the midpoint of the diagonal BD; if BM bisects ∠ABC, then the value of ∠AMB is

1. 45°
2. 60°
3. 90°
4. 75°

Solution: The correct answer is 3. 90°

⇒ In parallelogram ABCD, AB || DC and BD its intersection.

∴ ∠ADB = alternate ∠DBC

⇒ ∠ADB = ∠ABD [BM is the bisector of ∠ABC]

∴ AB = AD

⇒ In ΔABM and ΔADM,

⇒ AB = AD, BM = DM [M is the midpoint of BD] and AM = AM [common side]

∴ ΔABM ≅ ΔADM [by S.S.S. criterion of congruency)

∴ ∠AMB = ∠AMD

⇒ Again, ∠AMB+ ∠AMD = 180°

⇒ ∠AMB + ∠AMB = 180°

⇒ 2 ∠AMB = 180°

⇒ ∠AMB = 90°

The value of ∠AMB is 90°

Example 5. In the rhombus ABCD, ∠ACB = 40°, the value of ∠ADB is

1. 50°
2. 110°
3. 90°
4. 120°

Solution: The correct answer is 1. 50°

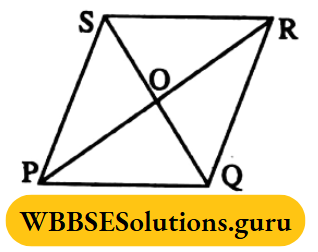
⇒ Let O is the point of intersection of diagonals AC and BD of rhombus ABCD.

⇒ The diagonals of rhombus bisect each other perpendicularly.

∴ ∠BOC = 90°

⇒ In ΔBOC, ∠OBC + ∠BOC + ∠OCB = 180°

⇒ ∠OBC + 90° + 40° = 180° [∠ACB = 40°]

⇒ or, ∠OBC = 50° i.e. ∠DBC = 50°

⇒ As DC || AB and BD is the intersection

∴ ∠ADB = alternate ∠DBC = 50°

The value of ∠ADB is 50°

Example 6. In parallelogram ABCD, if ∠A : ∠B = \(\frac{1}{2}\):\(\frac{1}{3}\),then the value of ∠C is

1. 90°
2. 36°
3. 72°
4. 108°

Solution: The correct answer is 4. 108°

⇒ ∠A: ∠B = \(\frac{1}{2}\):\(\frac{1}{3}\) = 3: 2

⇒ ∠A + ∠B = 180°

⇒ ∠A = 180°x \(\frac{3}{3 + 2}\) = 180° x \(\frac{3}{5}\)=108°

⇒ ∠C = ∠A = 108°

⇒ [Opposite angle of parallelogram are equal]

The value of ∠C is 108°

Example 7. The perimeter of a parallelogram is 22 cm. If the longer side measures 6.5 cm, then the measure of the shorter side is

1. 9 cm
2. 7.5 cm
3. 4.5 cm
4. 11 cm

Solution: The sum of two longer sides is (6.5 x 2) cm or 13 cm.

⇒ The sum of two shorter sides is (22 – 13) cm or 9 cm.

∴ The length of the shorter side is \(\frac{9}{2}\) cm or 4.5 cm.

∴ The correct answer is 3. 4.5 cm

Example 8. If the ratio of consecutive angles of a quadrilateral is 2: 1:3: 4, then the quadrilateral will be

1. Parallelogram
2. Square
3. Rhombus
4. None of them

Solution: The correct answer is 4. None of them

⇒ Let the angles are 2x°, x°, 3x°, 4x° [Where x is common multiple and x > 0]

⇒ 2x + x + 3x + 4x = 360°

⇒ 10x = 360 ⇒ x = 36

∴ The angles are 36 x 2° 72°, 36°, 3 x 36° or 108°, 4 x 36° or 144°

{Opposite angle are not equal}