WBBSE Class 9 Maths Geometry Chapter 3 Theorems On Area Multiple Choice Questions

WBBSE Class 9 Maths Geometry Chapter 3 Theorems On Area Multiple Choice Questions

Example 1. D, E, and F are midpoints of sides BC, CA, and AB respectively of a triangle ABC. If ΔABC = 16 sq. cm, then the area of the trapezium-shaped region FBCE.

1. 50 sq. cm
2. 8 sq. cm
3. 12 sq. cm
4. 100 sq. cm

Solution: The correct answer is 3. 12 sq. cm

Read and Learn More WBBSE Class 9 Maths Multiple Choice Questions

⇒ In ΔABC, F and E are the midpoints of AB and AC respectively.

∴ FE || BC or, FE || BD

⇒ Similarly, DE || BF

⇒ In quadrilateral BDEF, FE || BD and BF || DE

∴ BDEF is a parallelogram whose one diagonal is FD

∴ ΔBDF ≅ ΔDEF

∴ ΔBDF = ΔDEF

⇒ Similarly, ΔDEF = ΔAEF and ΔDEF = ΔCDE

∴ ΔDEF = ΔBDF = ΔAEF = ΔCDE

⇒ ΔDEF + ΔBDF + ΔAEF + ΔCDE = ΔABC

∴ ΔDEF + ΔDEF + ΔDEF +ΔDEF

⇒ or, 4 ΔDEF 16 sq. cm

⇒ or, ΔDEF = 4 sq. cm

∴ ΔBDF = ΔCDE = 4 cq. cm

∴ Area of the trapezium shaped region FBCE = ΔBDF + ΔDEF + ΔCDE

∴ Area of the trapezium shaped region FBCE = (4 + 4 + 4) sq. cm = 12 sq. cm

Example 2. A, B, C, and D are the midpoints of sides PQ, QR, RS, and SP respectively of the parallelogram PQRS. If area of the parallelogram-shaped region PQRS = 36 sq. cm then area of the region ABCD is

1. 24 sq. cm
2. 18 sq. cm
3. 30 sq. cm
4. 36 sq. cm

Solution: The correct answer is 4. 36 sq. cm

I join D, B.

⇒ In quadrilateral PQBD, PD || QB  [PS || QR]

⇒ and PD = QB  [\(\frac{1}{2}\) PS = \(\frac{1}{2}\) QR]

∴ PQRS is a parallelogram,  ∴ DB || PQ

⇒ Similarly, DBRS is a parallelogram

⇒ ΔABD and parallelogram PQBD, are on same base DB and between same parallels DB and PQ

⇒ ΔABD = \(\frac{1}{2}\) parallelogram PQBD

⇒ Similarly, ΔBCD = \(\frac{1}{2}\) parallelogram DBRS

⇒ ΔABD = ΔBCD = \(\frac{1}{2}\) [parallelogram PQBD + parallelogram DBRS]

⇒ i.e. quadrilateral ABCD = \(\frac{1}{2}\) parallelogram PQRS

∴ Area of quadrilateral ABCD = (\(\frac{1}{2}\) x36) sq cm = 18 sq. cm

Example 3. O is any a point inside parallelogram ABCD. If ΔAOB + ΔCOD = 16 sq. cm, then area of the parallelogram-shaped region ABCD is

1. 8 sq. cm
2. 4 sq. cm
3. 32 sq. cm
4. 64 sq. cm

Solution: The correct answer is 3. 32 sq. cm

⇒ Through the point O a straight line parallel to AB or CD is drawn which intersects the sides AD and BC at the points E and F respectively.

⇒ In quadrilateral ΔBFE, AB || EF and AE || BF

∴ ABFE is a parallelogram.

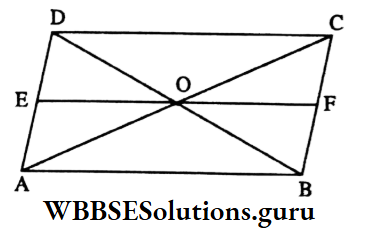
⇒ ΔAOB and parallelogram ABFE, are on same base AB and between same parallels AB and EF

∴ ΔAOB = \(\frac{1}{2}\) parallelogram ABFE

⇒ Similarly, ΔCOD = \(\frac{1}{2}\) parallelogram CDEF

⇒ ΔAOB+ ΔCOD = \(\frac{1}{2}\)(parallelogram ABFE + parallelogram CDEF)

⇒ 16 sq. cm = \(\frac{1}{2}\) parallelogram ABCD

⇒ or, Area of parallelogram = 32 sq. cm

Example 4. D is the midpoint of side BC of triangle ABC. E is the midpoint of side BD and O is the midpoint of AE; area of triangular field BOE is

1. \(\frac{1}{3}\) x Area of ΔABC
2. \(\frac{1}{4}\) x Area of ΔABC
3. \(\frac{1}{6}\) x Area of ΔABC
4. \(\frac{1}{8}\) x Area of ΔABC

Solution: The correct answer is 4. \(\frac{1}{8}\) x Area of ΔABC

⇒ I join A and D.

⇒ AD is a median of ΔABC

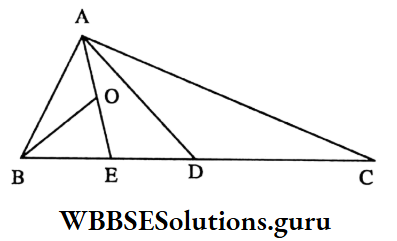
∴ ΔABD = \(\frac{1}{2}\) ΔABC

⇒ AE is a median of ΔABD

∴ ΔABE = \(\frac{1}{2}\) ΔABD

⇒ BO is a median of ΔABE

∴ ΔBOE = \(\frac{1}{2}\) ΔABE = \(\frac{1}{2}\) x \(\frac{1}{2}\) ΔABD = \(\frac{1}{4}\) x \(\frac{1}{2}\) ΔABC = \(\frac{1}{8}\) ΔABC

Example 5. A parallelogram, a rectangle, and a triangular region stand on same base and between same parallel, and it their area are P, R, and T respectively then

1. P = R = 2T
2. P = R = \(\frac{T}{2}\)
3. 2P = 2R = T
4. P = R = T

Solution: The correct answer is 1. P = R = 2T

⇒ If a parallelogram and a rectangle are on same base and between same parallel, then area of the parallelogram and rectangle are equal [As the rectangle is a parallelogram]

∴ P = R

⇒ Again a parallelogram and a triangle are on same base and between same parallel.

∴ Area of triangle is equal to half of area of parallelogram.

∴ T = \(\frac{P}{2}\)

or, P = 2T

∴ P = R = 2T

Example 6. The points D and E on sides BC of a triangle ABC such that BD = DE = EC; If the area of ΔABC is 12 sq. cm then the area of ΔABC is

1. 6 sq. cm
2. 12 sq. cm
3. 18 sq. cm
4. 24 sq. sm

Solution: The correct answer is 3. 18 sq. cm

⇒ AD is a median of ΔABE

∴ ΔADE = ΔABD = \(\frac{1}{2}\) ΔABE

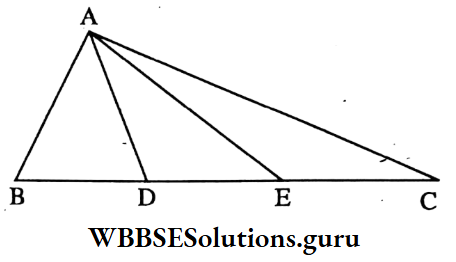
= (\(\frac{1}{2}\) x 12) sq. cm = 6 sq. cm

⇒ AE is a median of ΔADC

∴ ΔABC = ΔABD + ΔADE + ΔAEC

= (6+6+6) sq. cm = 18 sq. cm

Example 7. In ΔABC, P is the midpoint of median AD. If area of ΔAPC is 12 sq. em then the area of ΔBPC is

1. 6 sq. cm
2. 12 sq. cm
3. 15 sq. cm
4. 24 sq. cm

Solution: The correct answer is 4. 24 sq. cm

⇒ CP is a median of ΔADC,

⇒ ΔDPC = ΔAPC = \(\frac{1}{2}\) ΔACD

⇒ or, ΔADC = 2 ΔAPC (2 x 12) sq. cm = 24 sq. cm

⇒ PD is a median of ΔBPC

∴ ΔBPD = ΔDPC = 12 sq. cm  [ΔAPC = ΔDPC]

⇒ ΔBPC = ΔBPD + ΔDPC

ΔBPC = (12 + 12) sq. cm = 24 sq. cm

Example 8. In ΔABC, D, E, and F are midpoints of sides BC, CA, and AB respectively. If area of trapezium ABDE is 15 sq. cm, then area of ΔABC is

1. 7.5 sq. cm
2. 12 sq. cm
3. 20 sq. cm
4. 30 sq. cm

Solution: The correct answer is 3. 20 sq. cm

⇒ I join E, F and F, D.

⇒ In ΔABC, D, and E are the midpoints of BC and AC respectively.

∴ DE || AB i.e. DE || AF and DE = \(\frac{1}{2}\) AB

⇒ or DE = AF

∴ AFDE is a parallelogram whose diagonal is EF.

∴ ΔDEF = ΔAEF

⇒ Similarly, ΔDEF= ΔBDF and ΔDEF = ΔCDE

∴ ΔAEF = ΔBDF = ΔCDE = ΔDEF = x sq. cm [say, x > 0]

⇒ Area of trapezium of ABDE = ΔAEF + ΔDEF + ΔBDF

=(x+x+x) sq. cm = 3x cm

⇒ According to question 3x = 15 or x = 5

⇒ ΔABC = ΔAEF + ΔBDF + ΔDEF+ ΔCDE = (5+5+5+5) sq. cm = 20 sq. cm