WBBSE Class 9 Maths Geometry Chapter 4 Theorems On Concurrence Multiple Choice Questions

WBBSE Class 9 Maths  Geometry Chapter 4 Theorems On Concurrence Multiple Choice Questions

Example 1. O is the circumcentre of ΔABC; if ∠BOC = 80°, the ΔBAC is

1. 40°
2. 160°
3. 130°
4. 110°

Solution: The correct answer is 1. 40°

Read and Learn More WBBSE Class 9 Maths Multiple Choice Questions

I join A, O and AO is extended at T.

⇔ In ΔAOB, OA = OB [circumradius]

∴ ∠OAB = ∠OBA

⇔ In ΔAOB, the exterior ∠BOT = ∠OAB+ ∠OBA

= ∠OAB + ∠OAB = 2 ∠OAB.

⇒ Similarly, ∠COT = 2 ∠OAC

⇒ ∠BOC = ∠BOT + ∠COT

⇒ ∠BOC = 2(∠OAB + ∠OAC)

⇒ 80° = 2 ∠BAC

⇒ or, ∠BAC 40°

Example 2. O is the orthocentre of ΔABC; if ∠BAC = 40°, the ∠BOC is

1. 80°
2. 140°
3. 110°
4. 40°

Solution: The correct answer is 2. 140°

⇔ In ΔABC, AD ⊥ BC, BE ⊥ CA and CF ⊥ AB.

⇒ As BE ⊥ AC,

∴ ∠AEO = 90°

⇒ CF ⊥ AB,

∴ ∠AFO = 90°

⇒ In quadrilateral AEOF,

⇒ ∠EAF + ∠AEO + ∠EOF+ ∠AFO = 360°

⇒ 40° + 90° + ∠EOF+ 90° = 360° [∠BAC= 40°]

⇒ ∠EOF = 140°

⇒ ∠BOC = vertically opposite ∠EOF= 140°

Example 3. O is the incentre of ΔABC; if ∠BAC 40°, then ∠BOC is

1. 80°
2. 110°
3. 140°
4. 40°

Solution: The correct answer is 110°

⇔ O is the incentre of ΔABC

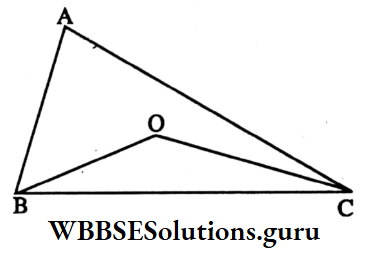
∴ ∠OBC = \(\frac{1}{2}\) ∠ABC and

∠OCB = \(\frac{1}{2}\) ∠ACB

∠OBC + ∠OCB = \(\frac{1}{2}\) (∠ABC + ∠ACB)

= \(\frac{1}{2}\) (180° – ∠BAC)

= \(\frac{1}{2}\) (180° – 40°) = 70°

In ΔBOC, ∠BOC = 180° – (∠OBC + ∠OCB)

= 180° – 70° = 110°

∠BOC = 110°

Example 4. G is the centroid of triangle ABC; if area of ΔGBC is 12 sq. cm, then the area of ΔABC is

1. 24 sq. cm
2. 6 sq. cm
3. 36 sq. cm
4. None of them

Solution: The correct answer is 3. 36 sq. cm

⇔ AD is a median of ΔABC

∴ ΔABD = ΔACD

⇒ GD is a median of ΔGBC

∴ ΔBGD = ΔCGD

∴ ΔABD – ΔBGD = ΔACD – ΔCGD

i.e. ΔAGB = ΔACG

⇒ Similarly, ΔABG = ΔGBC

∴ ΔABG = ΔACG = ΔGBC

⇒ ΔABG + ΔACG + ΔGBC = ΔABC

⇒ ΔGBC + ΔGBC + ΔGBC = ΔABC

⇒ΔABC = 3 ΔGBC

= (3 x 12) sq. cm = 36 sq. cm.

The area of ΔABC is = 36 sq. cm.

Example 5. If the length of circumradius of a right-angled triangle is 5 cm, then the length of the hypotenuse is

1. 2.5 cm
2. 10 cm
3. 5 cm
4. None of these

Solution: The correct answer is 2. 10 cm

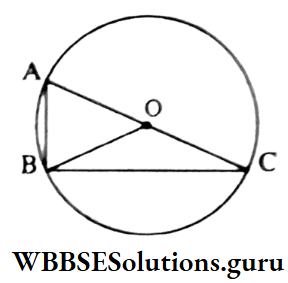
⇒ The circumcentre of a right-angled triangle is on the midpoint of hypotenuse.

⇒ The length of hypotenuse = 2 x circumradius

= (2 × 5) cm = 10 cm

The length of hypotenuse = 10 cm

Example 6. If the length of two median of a triangle are equal, then the triangle will be

1. Equilateral triangle
2. Isosceles triangle
3. Scalene triangle
4. None of them

Solution: The correct answer is 2. Isosceles triangle

⇔ In ΔABC, two medians intersect at G (centroid).

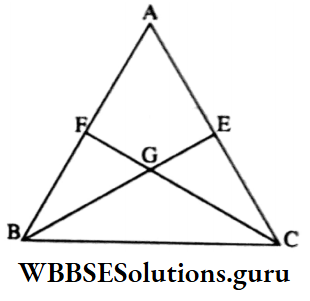
⇒ BE = CF [Given]

⇒ BG: GE = 2: 1 and CG: GF = 2:1

⇒ \(\frac{\mathrm{BG}}{\mathrm{GE}}=\frac{2}{1}\)

⇒ or, \(\frac{\mathrm{GE}}{\mathrm{BG}}=\frac{2}{1}\)

⇒ or, \(\frac{\mathrm{GE}}{\mathrm{BG}}+1=\frac{1}{2}+1\)

⇒ or, \(\frac{\mathrm{BE}}{\mathrm{BG}}=\frac{3}{2}\)

⇒ or, \(\mathrm{BG}=\frac{2}{3} \mathrm{BE}\)

⇒ Similarly, CG = \(\frac{2}{3}\) CF

⇒ BE = CF

⇒ or, \(\frac{2}{3}\) BE = \(\frac{2}{3}\) CF

∴ BG = CG

⇒ BE – BG = CF – CG i.e., GE GF

⇒ In ΔBGF and ΔCGE, BG = CG, GF = GE and ∠BGF = ∠CGE [vertically opposite angle]

∴ ΔBGF ≅ ΔCGE [by, SAS criterion of congruency]

∴ FB = EC

⇒ or, \(\frac{1}{2}\) AB = \(\frac{1}{3}\) AC

⇒ or, AB = AC

∴ ΔABC is a isosceles triangle.

Example 7. If the length of circum-radius of a equilateral triangle is 6 cm, then the perimeter of the triangle is

1. 6√3 cm
2. 12 cm
3. 18√3 cm
4. 3√/2 cm

Solution: The correct answer is 3. 18√3 cm

⇒ In an equilateral triangle, circumcentre and centroid are coincide.

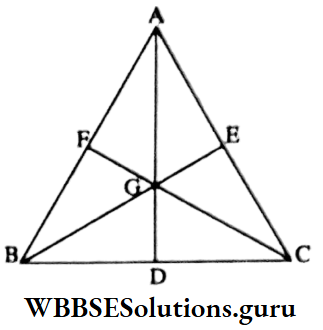
⇔ In equilateral triangle ABC, the medians AD and BE intersects at point G (centroid).

⇒ The length of circumradius (AG) is 6 cm.

⇒ Again, AG : GD = 2:1

∴ GD = (\(\frac{1}{2}\) x 6) cm = 3 cm

⇒ AD = AG+ GD (6 + 3) cm = 9 cm

⇒ If the length of each side is x cm then the height of triangle is \(\frac{\sqrt{3}}{2}\) x cm [x > 0]

⇒ \(\frac{\sqrt{3x}}{2}\) = 9

⇒ or, x = \(\frac{9 \times 2}{\sqrt{3}}\) = 3√3 x 2 = 6√3

∴ Perimeter of the triangle is (3 x 6√3) cm = 18√3 cm

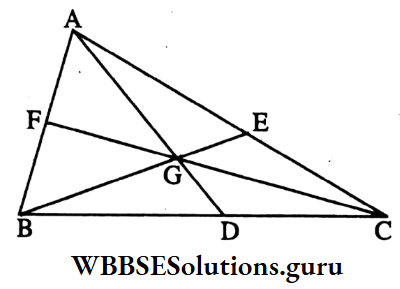
Example 8. If the three medians of ΔABC are AD, BE and CF, then

1. AB + BC + CA > AD + BE + CF
2. AB + BC + CA < AD + BE + CF
3. AB + BC + CA = AD + BE + CF
4. None of them

Solution: The correct answer is 1. AB + BC + CA > AD + BE + CF

⇔ AD is extended at P such that AD = DP;

I join C, P.

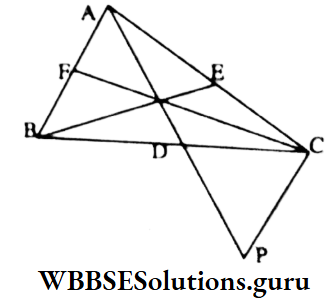
In ΔABD and ΔCDP,

BD = CD, AD = DP and ∠ADB = ∠CDP [vertically opposite angles]

∴ ΔABD ≅ ΔCDP [by S-A-S criterion of congruency]

∴ AB = CP

In ΔAPC, AC + CP > AP [Sum of length of two sides of a triangle is greater than the length of third side]

∴ AC + AB > AD + PD

AB + AC > AD + AD

AB + AC > 2 AD …….(1)

Similarly BC + AC > 2 CF……(2)

and AB = BC > 2BE…..(3)

(1) + (2) + (3) we get,

2(AB + BC + CA) = 2(AD+ BE + CF)

⇒ AB + BC + CA > AD + BE + CF