WBBSE Class 9 Coordinate Geometry Chapter 3 Area Of Triangular Region Multiple Choice Questions

WBBSE Class 9  Coordinate Geometry Chapter 3 Area Of Triangular Region Multiple Choice Questions

Example 1. The area of triangular formed by three points (0, 4), (0, 0), (-6, 0) is

1. 24 sq. unit
2. 12 sq. unit
3. 6 sq. unit
4. 8 sq. unit

Solution: Area = \(\frac{1}{2}|0+0-24-(0+0+0)|\) sq. unit = 12 sq. unit

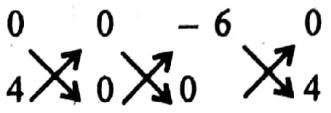
Example 2. The coordinates of the centroid of a triangle formed by three points (7, -5), (-2, 5), and (4, 6) is

1. (3,-2)
2. (2, 3)
3. (3, 2)
4. (2, -3)

Solution: \(\left(\frac{7-2+4}{3}, \frac{-5+5+6}{3}\right)=(3,2)\)

Example 3. ΔABC is a right-angled triangle of which ∠B = ordinates of A, C are (0, 4) and (3, 0). The area of two triangles is

1. 12 sq. unit
2. 6 sq. unit
3. 24 sq. unit
4. 8 sq. unit

Solution: Area = \(\frac{1}{2}\) x 3 x 4 sq. u = 6 sq. unit

 

 

 

 

 

 

WBBSE Solutions For Class 9 Fundamentals Of History	WBBSE Class 9 English Functional Grammar
WBBSE Class 9 Fundamentals Of History Long Answer Questions	WBBSE Class 9 English Reading Skill
WBBSE Class 9 Fundamentals Of History Short Answer Questions	WBBSE Class 9 English Writing Skill
WBBSE Class 9 Fundamentals Of History Very Short Answer Questions	WBBSE Class 9 Maths Multiple Choice Questions
WBBSE Class 9 Fundamentals Of History Multiple Choice Questions	WBBSE Solutions For Class 9 Maths
WBBSE Notes For Class 9 Geography and Environment

 

Example 4. If (0, 0), (+4, -3), (x, y) are collinear then

1. x = 8, y = -6
2. x = 8, y = 6
3. x = 4, y = 6
4. x = 8, y = 6

Solution:

\(\frac{1}{2}|0+4 y+0-(0-3 x)|=0\)

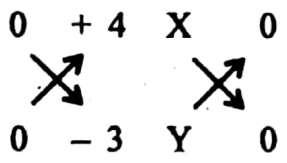
or, \(\left|+2 y+\frac{3}{2} x\right|=0\)

x = +8, y = 6 satisfies the equations.

 

 

 

 

 

 

 

 

 

 

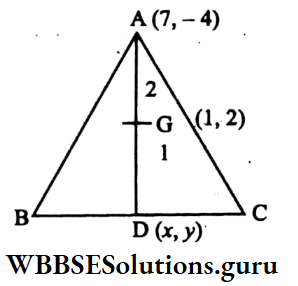
Example 5. If in triangle ABC, the co-ordinates of vertex A is (7, -4) and the centroid of the triangle is (1, 2) then the co-ordinates of midpoint of BC is

1. (-2,-5)
2. (-2, 5)
3. (2, -5)
4. (5, -2)

Solution: AG: GD = 2:1

Let the Co-ordinate of D be (x, y)

∴ \(\frac{2 x+7}{3}=1 \quad \frac{2 y-4}{3}=2\)

or, x = -2 or, y = 5

 

 

 

 

 

 

Example 6. (-1, 3), (2, k) and (5, -1) are collinear. k =

1. 1
2. 0
3. 2
4. None of these

Solution:

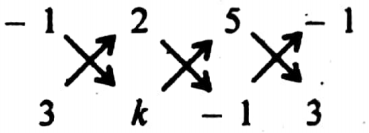
= \(\frac{1}{2}|-k+13-7-5 k|=0 \Rightarrow k=1\)

Example 7. The points (9, 0), (0, 4), (2, 2) are colinear if

1. a + b = 2
2. a + b + 4 = 0
3. \(\frac{1}{a}+\frac{1}{b}=\frac{1}{2}\)
4. ab = 2

Solution:

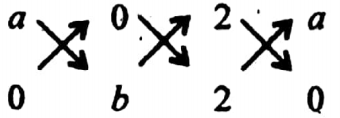
= \(\frac{1}{2}|a b+0+0-2 b-2 a|=0 \text { or, } a b=2 b+2 a \text { or, } \frac{1}{a}+\frac{1}{b}=\frac{1}{2}\)

Example 8. If the points (a, 0), (0, 4), (1, 1) are on the same straight line then

1. \(\frac{1}{a}+\frac{1}{b}\) = 1
2. ab = 1
3. a+b+1=0
4. None of these

Solution:

= \(\frac{1}{2}|a b-b-a|=0\)

a + b = ab

\(\frac{1}{a}+\frac{1}{b}=1\)