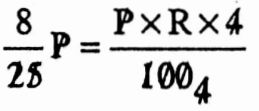Haritha

Trigonometry Chapter 4 Application Of Trigonometric Ratios Height And Distance

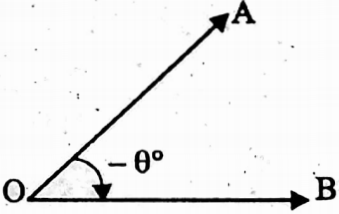
⇔ The angle of Elevation: When an observer stands on a base, the point being viewed is above the horizontal level, the angle formed by the line of sight, of an observer with a horizontal line, is called the angle of elevation.

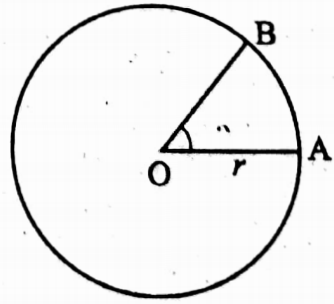
⇒ ∠AOP is the angle of elevation.

⇔ The angle of Depression: When the observer is looking down at an object, then the angle so formed by his line of sight with the horizontal line is called the angle of depression.

⇒ ∠BPO is the angle of depression.

⇒ As BP || OA

∴ Angle of elevation = Angle of depression

Read and Learn More WBBSE Solutions for Class 10 Maths

Trigonometry Chapter 4 Application Of Trigonometric Ratios Height And Distance True Or False

Example 1. In ΔABC, ∠B = 90°, if AB = BC then ∠C = 60°.

Solution: In ΔABC, ∠B = 90°

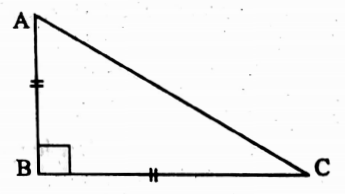
⇒ tan C = \(\frac{AB}{BC}\)

= \(\frac{AB}{AB}\) [as AB = BC]

= 1

⇒ tan C = tan 45° ⇒ ∠C = 45°

∴ The statement is false.

Example 2. PQ is the height of a building, QR is the base, and the angle of depression from a point R is ∠SPR; So, ∠SPR = ∠PRQ.

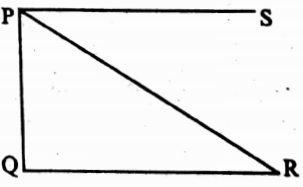
Solution: Clearly, the statement is true.

Class 10 Maths Trigonometry Chapter 4 Solutions

Example 3. If the angle of depression of a point is 30°, then the angle of elevation of that point is 30°

Solution: AB || DC and AC is intersection

∴ ∠ACB = ∠BAC = 30°

∴ The statement is true.

Example 4. If the length of the shadow on the ground of a post is \(\frac{1}{\sqrt{3}}\) times its height, then the angle of elevation is 60°

Solution: AB is the height and BC is the shadow of the post.

∠ABC = 90°, Let angle of elevation is θ.

∴ ∠ACB = θ and BC = \(\frac{A B}{\sqrt{3}}\)

tan θ = \(\frac{AB}{BC}\) = √3

⇒ tan θ = tan 60°

⇒ θ = 60°

∴ The statement is true

Trigonometry Chapter 4 Application Of Trigonometric Ratios Height And Distance Fill In The Blanks

Example 1. If the sun’s angle of elevation increases from 30° to 60°, the length of the shadow of a post _______ (decreases / increases).

Solution: When the angle of elevation is 30° then the length of the shadow of the post-AB is BD; If the angle of elevation is 60°, then the length of the shadow of AB is BC; As BD > BC.

∴ The length of the shadow of a post decreases.

Example 2. If the angle of elevation of sun is 45°, the length of shadow and length of post are _________

Solution: Let the length of the post is AB and the length of its shadow is BC

In ΔABC, \(\frac{AB}{BC}\) = tan 45°

\(\frac{AB}{BC}\) = 1

AB = BC

∴ Length of the shadow and the length of the post are equal.

Trigonometric Equations Class 10 Solutions

Example 3. If the angle of elevation of the sun is ________ 45°, the length of the shadow of the tower will be less than the height of tower.

Solution: Greater

[BD > BC]

Example 4. If the angle of elevation of sun decreases from 65° to 50°, the length of the shadow of a tower _______

Solution: increases.

Trigonometry Chapter 4 Application Of Trigonometric Ratios Height And Distance Short Answer Type Questions

Example 1. If the angle of elevation of a kite is 60° and the length of the thread is 20√3 metres, then calculate the height of the kite above the ground.

Solution: Let the height of the kite above the ground is AB and the length of the thread is AC.

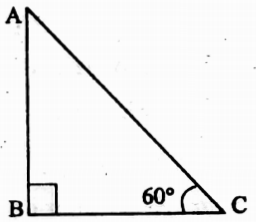
The angle of elevation of the kite is ∠ACB

So, ∠ACB = 60° and AC = 20√3 metres.

In ΔABC, \(\frac{AB}{AC}\) = sin 60°

⇒ \(\frac{A B}{20 \sqrt{3}}m=\frac{\sqrt{3}}{2}\)

⇒ AB = \(\frac{60}{2}\) metre = 30 metre.

∴ The height of the kite is 30 metres.

Example 2. AC is the hypotenuse witha length of 100 metres of a right-angled triangle ABC and if AB = 50√3 metre, then find the value of ∠C.

Solution: In ΔABC, ∠ABC = 90°

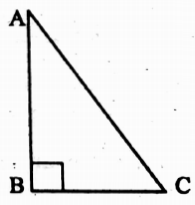
∴ sin C = \(\frac{AB}{AC}\)

sin C = \(\frac{50 \sqrt{3}}{100}=\frac{\sqrt{3}}{2}\)

⇒ sin C = sin 60°

⇒ ∠C = 60°

Class 10 Trigonometry Chapter 4 Solved Examples

Example 3. A tree breaks due to storm and its top touches the ground in such a manner that the distance from the top of the tree to the base of the tree and present height are equal. Calculate how much angle is made by the top of the tree with the base.

Solution: Let the present height of the tree is AB and the distance from the top of the tree to the base of the tree is BC where AB = AC

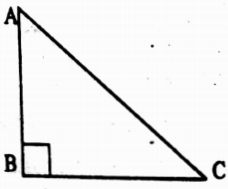
⇒ tan ∠ACB = \(\frac{AB}{BC}\) = \(\frac{AB}{AB}\) = 1

⇒ tan ∠ACB = tan 45°

⇒ ∠ACB = 45°

∴ The angle is 45°

Example 4. In the right-angled triangle, ABC, ∠B = 90°, D is such a point on AB that AB: BC: BD = √3: 1: 1. Find the value of ∠ACD.

Solution: AB : BC : BD = √3 : 1 : 1

Let AB = √3 x unit, BC = x unit and BD = x unit where x is common multiple and x > 0.

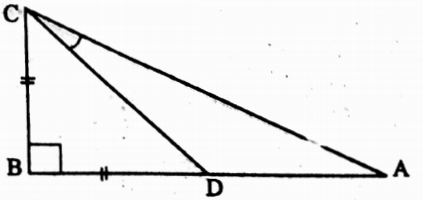
In ΔDBC, ∠DBC = 90°

tan ∠BDC = \(\frac{BC}{BD}\) = \(\frac{x}{x}\) = 1

⇒ tan ∠BDC = tan 45° ⇒ ∠BDC = 45°

In ΔABC, tan ∠BAC = \(\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{x}{\sqrt{3} x}=\frac{1}{\sqrt{3}}\)

⇒ tan ∠BAC = tan 30°

⇒ ∠BAC = 30° i.e. ∠DAC = 30°

∴ ∠ACD = ∠BDC – ∠DAC = 45° – 30° = 15°

∴ The value of ∠ACD is 15°.

Example 5. If the ratio between length of shadow of a tower and height of tower is 3: 1, find the angle of elevation of the sun.

Solution: Let length of shadow of a tower is BC and height of tower is AB.

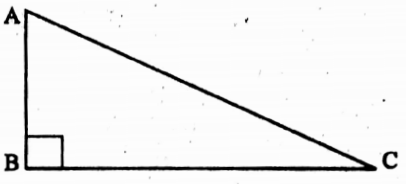
Where = \(\frac{\mathrm{BC}}{\mathrm{AP}}=\frac{\sqrt{3}}{1}\)

The angle of elevation of tower is ∠ACB

∴ In ΔABC, ∠ABC = 90°

∴ tan ACB = \(\frac{A B}{B C}=\frac{1}{\sqrt{3}}\)

⇒ tan ∠ACB = tan 30°

⇒ ∠ACB = 30°

∴ The angle of elevation is 30°.

Wbbse Class 10 Trigonometry Notes

Example 6. The angles of elevation of the top of a tower from two points at a distance 4 metres and 9 metres from the base and in the same straight line with it are complementary, hind the height of the tower.

Solution: Let the height of the tower AB is h metre, [h > 0]

Let C and D be two points at distances 4 metres and 9 metres respectively from the base of the tower.

BC = 4 metre and BD = 9 metre.

Let ∠ADB = θ and ∠ACB = 90° – θ

In ΔADB, ∠B = 90° tanθ = \(\frac{AB}{BD}\)

⇒ tanθ = \(\frac{h}{9}\)……(1)

In ΔABC, tan (90°- θ) = \(\frac{AB}{BC}\)

⇒ cotθ = \(\frac{h}{4}\)……..(2)

From (1) and (2), we have,

\(\frac{h}{9}\) x \(\frac{h}{4}\) = tanθ.cotθ

⇒ \(\frac{h^2}{36}=1\) ⇒ h² = 36 ⇒ h = √36 = 6

∴ The length of the tower is 6 metre.

Example 7. If AB = 5 m and BC = 5√3 m, then find the value of θ.

Solution: tanθ = \(\frac{A B}{B C}=\frac{5}{5 \sqrt{3}}=\frac{1}{\sqrt{3}}\)

⇒ tanθ = tan 30°

⇒ θ = 30°

Solving Trigonometric Equations Class 10

Example 8. On the same side of a house, two objects are located. When observed from the top of the house, their angles of depression are 45° and 60°. If the height of the house is 50 m find the distance between the objects.

Solution: Let, the height of the house = AB = 50m.

Distance between the two objects = CD = x m. [x>0]

BC = y m [y>0]

The angle of depression from the point A of AB at the point C is 60° and angle of depression at the point D is 45°.

∴ ∠CAE = 60° and ∠DAE = 45°

∴ ∠ACB = ∠CAE = 60° [As AE || BD]

and ∠ADB = ∠DAE = 45°

In ΔABC, ∠ABC = 90°

∴ \(\frac{AB}{BC}\) = tan 60°

⇒ \(\frac{50}{y}\) = √3

⇒ y = \(\frac{50}{\sqrt{3}}\)

In ΔABD, \(\frac{AB}{BD}\) = tan 45°

\(\frac{50}{y+x}\) = 1

Class 10 Maths Trigonometry Important Questions 

⇒ x + y = 50

x = 50 – y = 50 – \(\frac{50}{\sqrt{3}}\) = 50 – \(\frac{50 \sqrt{3}}{3}\)

= 50 – \(\frac{50 \times 1 \cdot 732}{3}\) = 50 – 28.87 = 21.13 (approx)

∴ The distance between the objects is 21.13 m (approx)

Trigonometry Chapter 3 Trigonometric Ratios Of Complementary

Trigonometric ratios of complementary angle:

⇔ sin (90° – θ) = cos θ

⇔ cos (90° – θ) = sin θ

⇔ tan (90° – θ) — cot θ

⇔ cot (90° – θ) = tan θ

⇔ sec (90° – θ) = cosec θ

⇔ cosec (90° – θ) = sec θ

Read and Learn More WBBSE Solutions for Class 10 Maths

Trigonometry Chapter 3 Trigonometric Ratios Of Complementary True Or False

Example 1. The value of cos 54° and sin 36° are equal.

Solution: cos 54° = cos (90° – 36°)

= sin 36°

∴ The statement is true.

Example 2. The simplified value of (sin 12° – cos 78°) is 1.

Solution: sin 12° – cos 78°

= sin 12° – cos (90° – 12°)

= sin 12° – sin 12° = 0

∴ The statement is false.

Example 3. If tan 3θ = cot 2θ and 3θ is a positive acute angle, then the value of θ is 18°.

Solution: tan 3θ= cot 2θ

⇒ tan 3θ = tan (90° – 2θ)

⇒ 3θ = 90° – 20

⇒ 3θ + 2θ = 90°

⇒ 5θ = 90°

⇒ θ = 18°

∴ The statement is True.

Example 4. If tan 5θ.tan 4θ = 1 and 5θ is positive acute angle ; then the value of sin 3θ is \(\frac{1}{\sqrt{2}}\)

Solution: tan 5θ.tan 4θ= 1

⇒ tan 5θ = \(\frac{1}{\tan 4 \theta}\)

⇒ tan 5θ = cot 4θ

⇒ tan 5θ= tan (90° – 4θ)

⇒ 5θ = 90° – 4θ

⇒ 9θ = 90°

⇒ θ = 10°

sin 3θ = sin 3 x 10° = sin 30° = \(\frac{1}{2}\)

∴ The statement is False.

Class 10 Maths Trigonometry Chapter 3 Solutions

Example 5. If cosθ = \(\frac{5}{13}\), then the value of cos (90° – θ) is \(\frac{12}{13}\).

Solution: cos (90° – θ)

= sinθ = \(\sqrt{1-\cos ^2} \theta\)

= \(\sqrt{1-\left(\frac{5}{13}\right)^2}=\sqrt{1-\frac{25}{169}}\)

= \(\sqrt{\frac{144}{169}}=\frac{12}{13}\)

∴ The statement is True.

Trigonometry Chapter 3 Trigonometric Ratios Of Complementary Fill In The Blanks

Example 1. The value of (tan 15° x tan 45° x tan 60° x tan 75°) is ______

Solution: tan 15° x tan 45° x tan 60° x tan 75°

= tan 15° x tan 45d x tan 60° x tan (90° – 15°)

= tan 15° x 1 x √3 x cot 15°

= tan 15° x √3 x \(\frac{1}{\tan 15^{\circ}}\) = √3

∴ Answer is √3

Example 2. The value of (sin 12° x cos 18° x sec 78° x cosec 72°) is ______

Solution: sin 12° x cos 18° x sec 78° x cosec 72°

= sin 12° x cos 18° x sec (90° – 12°) x cosec (90° – 18°)

= sin 12° x cos 18° x cosec 12° x sec 18°

= sin 12° x cos 12° x \(\frac{1}{\sin 12^{\circ}}\) x \(\frac{1}{\cos 18^{\circ}}\)

= 1

Example 3. If A and B are complementary to each other, sin A = ______

Solution: A + B = 90°

sin A = sin (90° – B) = cos B

Wbbse Class 10 Maths Trigonometry Solutions

Example 4. The value of sec 52° sin 38° is ______

Solution: sec 52° sin 38°

= sec 52° sin (90° – 52°)

= sec 52° cos 52°

= sec 52° x \(\frac{1}{\sec 52^{\circ}}\) = 1

∴ Answer is 1.

Example 5. If α + β = 90°, then the value of (1 – tanα.tanβ) is _______

Solution: 1 – tanα.tanβ

= 1 – tanα.tan (90° – α)

= 1 – tanα.cotα

= 1-1 = 0

∴ Answer is zero.

Trigonometric Identities Class 10 Solutions

Trigonometry Chapter 3 Trigonometric Ratios Of Complementary Short Answer Type Question

Example 1. If sin 10θ = cos 8θ and 10θ is a positive acute angle, find the value of tan 9θ.

Solution: sin 10θ = cos 8θ

⇒ sin 10θ = sin (90° – 8θ)

⇒ 10θ = 90° – 8θ

⇒ 18θ = 90°

⇒ θ = 5°

∴ tan 9θ = tan 9 x 5° = tan 45° = 1

Example 2. If tan 4θ x tan 6θ = 1 and 6θ is a positive acute angle, then find the value of θ.

Solution: tan 4θ x tan 6θ= 1

⇒ tan 4θ = \(\frac{1}{\tan 6 \theta}\)

⇒ tan 4θ = cot 6θ

⇒ tan 4θ = tan (90° – 6θ)

⇒ 4θ = 90° – 6θ

⇒ 10θ = 90°

⇒ θ = 9°

Example 3. Find the value of \(\frac{2 \sin ^2 63^{\circ}+1+2 \sin ^2 27^{\circ}}{3 \cos ^2 17^{\circ}-2+3 \cos ^2 73^{\circ}}\)

Solution: \(\frac{2 \sin ^2 63^{\circ}+1+2 \sin ^2 27^{\circ}}{3 \cos ^2 17^{\circ}-2+3 \cos ^2 73^{\circ}}\)

= \(\frac{2 \sin ^2 63^{\circ}+1+2 \sin ^2\left(90^{\circ}-63^{\circ}\right)}{3 \cos ^2 17^{\circ}-2+3 \cos ^2\left(90^{\circ}-17^{\circ}\right)}\)

= \(\frac{2 \sin ^2 63^{\circ}+1+2 \cos ^2 63^{\circ}}{3 \cos ^2 17^{\circ}-2+3 \sin ^2 17^{\circ}}\)

= \(\frac{2\left(\sin ^2 63^{\circ}+\cos ^2 63^{\circ}\right)+1}{3\left(\cos ^2 17^{\circ}+\sin ^2 17^{\circ}\right)-2}\)

= \(\frac{2 \times 1+1}{3 \times 1-2}=\frac{3}{1}=3\)

Example 4. Find the value of tan 1° x tan 2° x tan 3° x…….. x tan 89°

Solution: tan 1° x tan 2° x tan 3° x …… x tan (90° – 2°) x tan (90° – 1°)

= tan 1° x tan 2° x tan 3° x …. x cot 2° x cot 1°

= (tan 1° x cot 1°) x (tan 2° x cot 2°) x ……..x (tan 44° x cot 44°) x tan 45°

= 1 x 1 = 1…… x 1 x 1 = 1

Example 5. If sec 5A = cosec (A + 36°) and 5A is a positive acute angle, then find the value of A.

Solution: sec 5A = cosec (A + 36°)

⇒ sec 5A = sec {90° – (A + 36°)}

⇒ 5A = 90° – A – 36°

⇒ 6A = 54°

⇒ A = 9°

Example 6. If sin (2θ + 45°) = cos (30° – θ) where (2θ + 45°) and (30° – θ) are positive acute angles then find the value of tan 40.

Solution: sin (2θ+ 45°) = cos (30° – θ)

⇒ sin (2θ + 45°) = sin {90° – (30° – θ)}

⇒ 2θ+ 45° = 90° – 30° + θ

⇒ 2θ – θ = 60° – 45°

⇒ θ = 15°

tan 4θ = tan 4 x 15° = tan 60° = √3

Class 10 Trigonometry Chapter 3 Solved Examples

Example 7. If tan θ = cot (n – 1) θ, then find the value of θ.

Solution: tan θ = cot (n – 1) θ

⇒ cot (90° – θ) = cot (nθ – θ)

⇒ 90° – θ = nθ – θ

⇒ nθ = 90°

⇒ θ = \(\frac{90^{\circ}}{n}\)

Example 8. Find the value of \(\sin ^2 \frac{\pi}{16}+\sin ^2 \frac{3 \pi}{16}+\sin ^2 \frac{5 \pi}{16}+\sin ^2 \frac{7 \pi}{16}\)

Solution: \(\sin ^2 \frac{\pi}{16}+\sin ^2 \frac{3 \pi}{16}+\sin ^2 \frac{5 \pi}{16}+\sin ^2 \frac{7 \pi}{16}\)

= \(\sin ^2 \frac{\pi}{16}+\sin ^2 \frac{3 \pi}{16}+\sin ^2\left(\frac{\pi}{2}-\frac{3 \pi}{16}\right)+\sin ^2\left(\frac{\pi}{2}-\frac{\pi}{16}\right)\)

= \(\sin ^2 \frac{\pi}{16}+\sin ^2 \frac{3 \pi}{16}+\cos ^2 \frac{3 \pi}{16}+\cos ^2 \frac{\pi}{16}\)

= \(\left(\sin ^2 \frac{\pi}{16}+\cos ^2 \frac{\pi}{16}\right)+\left(\sin ^2 \frac{3 \pi}{16}+\cos ^2 \frac{3 \pi}{16}\right)\)

= 1 + 1 = 2

Example 9. Find the value of tan 20° tan 35° tan 45° tan 55° tan 70°

Solution: tan 20° tan 35° tan 45° tan 55° tan 70°

= tan 20° tan 35° tan 45° tan (90° – 35°) tan (90° – 20°)

= tan 20° tan 35° x 1 x cot 35° x cot 20°

= tan 20° tan 35° x tan 35° x \(\frac{1}{\tan 35^{\circ}} \times \frac{1}{\tan 20^{\circ}}\) = 1

Wbbse Class 10 Trigonometry Notes

Example 10. If x sinθ  – y cosθ = 3 and x cosθ+ y sinθ = 4 then find the value of \(\sqrt{x^2+y^2}\).

Solution: (x sinθ – y cosθ)² + (x cosθ + y sinθ)² = 3² + 4²

⇒ x² sin² θ – 2xy sinθ cosθ + y²cos² θ+ x²cos² θ + 2xy sinθ cosθ + y² sin² θ = 25

⇒ x² (sin² θ + cos² θ) + y2 (sin² θ + cos² θ) = 25

⇒ x² x 1 + y² x 1 = 25

⇒ \(\sqrt{x^2+y^2}= \pm \sqrt{25}= \pm 5\)

Trigonometry Chapter 2 Trigonometric Ratios And Trigonometric Identities

Trigonometric ratios:

⇔ In ΔABC, ∠ABC = 90° and ∠ACB = θ.

⇔ sin θ = \(\frac{\text { perpendicular }}{\text { hypotenuse }}=\frac{\mathrm{AB}}{\mathrm{AC}}\)

⇔ cos θ = \(\frac{\text { base }}{\text { hypotenuse }}=\frac{\mathrm{BC}}{\mathrm{AC}}\)

⇔ tan θ = \(\frac{\text { perpendicular }}{\text { base }}=\frac{\mathrm{AB}}{\mathrm{BC}}\)

⇔ cosec θ = \(\frac{\text { hypotenuse }}{\text { perpendicular }}=\frac{\mathrm{AC}}{\mathrm{AB}}\)

⇔ sec θ = \(\frac{\text { hypotenuse }}{\text { base }}=\frac{\mathrm{AC}}{\mathrm{BC}}\)

⇔ cot θ = \(\frac{\text { base }}{\text { perpendicular }}=\frac{\mathrm{BC}}{\mathrm{AB}}\)

∴ sin θ = \(\frac{1}{cosec \theta}\)

Read and Learn More WBBSE Solutions for Class 10 Maths

⇒ sin θ.cosec θ = 1

⇔ cos θ = \(\frac{1}{sec \theta}\)

⇒ cos θ.sec θ = 1

⇔ tan θ = \(\frac{1}{cot \theta}\)

⇒ tan θ.cot θ = 1

⇔ \(\tan \theta=\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{\frac{\mathrm{AB}}{\mathrm{AC}}}{\frac{\mathrm{BC}}{\mathrm{CA}}}=\frac{\sin \theta}{\cos \theta}\)

⇔ \(\cot \theta=\frac{\cos \theta}{\sin \theta}\)

Class 10 Maths Trigonometry Chapter 2 Solutions

Some Trigonometric identities of an acute angle:

1. sin² θ+ cos² θ = 1
2. sec² θ= 1 + tan² θ
3. cosec² θ = 1 + cot² θ

Following tables gives the values of trigonometric ratios :

Trigonometry Chapter 2 Trigonometric Ratios And Trigonometric Identities True Or False

Example 1. The value of tan A is always greater than 1.

Solution:

tan A = \(\frac{\mathrm{BC}}{\mathrm{AC}}\)

tan A = \(\frac{\mathrm{BC}}{\mathrm{BC}}\) [If BC = AC] = 1

tan A < 1 [If BC < AC]

tan A > 1 [If BC > AC]

So the statement is false.

Example 2. The value of cot A is always less tan 1.

Solution:

cot A = \(\frac{\mathrm{AC}}{\mathrm{BC}}\)

cotA = \(\frac{\mathrm{AC}}{\mathrm{AC}}\) [If AC = BC]

cot A = 1

cot A < 1 [If AC < BC]

cot A > 1 [If AC > BC]

∴ So the statement is false.

Wbbse Class 10 Maths Trigonometry Solutions

Example 3. For an angle θ, it may be possible that, sin θ = \(\frac{4}{3}\)

Solution:

sin θ = \(\frac{\mathrm{AB}}{\mathrm{AC}}\)

In a right-angled triangle hypotenuse is always greater than each of other two sides

∴ AB < AC  i.e. \(\frac{\mathrm{AB}}{\mathrm{AC}}\) < 1

∴ sin θ < 1

∴ The statement is false.

Example 4. For an angle α, it may be possible that, sec α = \(\frac{12}{5}\)

Solution:

sec α = \(\frac{\mathrm{AC}}{\mathrm{BC}}\)

as AC > BC [hypotenuse > side]

i.e. \(\frac{\mathrm{AC}}{\mathrm{BC}}\) > 1  ∴ sec α > 1

∴ The statement is true.

Heights And Distances Class 10 Solutions

Example 5. For an angle β, it may be possible that, cosec β= \(\frac{5}{13}\)

Solution:

cosec β = \(\frac{\mathrm{AC}}{\mathrm{AB}}\)

and AC > AB i.e. \(\frac{\mathrm{AC}}{\mathrm{AB}}\) > 1 ∴ cosec β > 1

∴ The statement is false.

Example 6. For an angle θ, is may be possible that, cos θ = \(\frac{3}{5}\)

Solution:

cos θ = \(\frac{\mathrm{BC}}{\mathrm{AC}}\)

BC < AC

i.e, \(\frac{\mathrm{BC}}{\mathrm{AC}}\) < 1 ∴ cos θ < 1

∴ The statement is true.

Example 7. If 0° ≤ α ≤ 90°, then the least value of (sec² α + cos² α) is 2.

Solution: sec² α + cos² α

= \(\frac{1}{\cos ^2 \alpha}+\cos ^2 \alpha\)

= \(\left(\frac{1}{\cos \alpha}-\cos \alpha\right)^2+2 \cdot \frac{1}{\cos \alpha} \cdot \cos \alpha\)

= \(\left(\frac{1}{\cos \alpha}-\cos \alpha\right)^2+2\)

∴ \(\left(\frac{1}{\cos \alpha}-\cos \alpha\right)^2 \geq 0\)

∴ The lease value of (sec² α + cos² α)

∴ The statements is true.

Example 8. The value of (cos 0° x cos 1° x cos 2° x cos 3° x…..x cos 90°) is 1.

Solution: (cos 0° x cos 1° x cos 2° x cos 3° x …… x cos 90°)

= cos 0° x cos 1° x cos 2° x ……. x 0 = 0

∴ The statement is false.

Class 10 Trigonometry Chapter 2 Solved Examples

Trigonometry Chapter 2 Trigonometric Ratios And Trigonometric Identities Fill In The Blanks

Example 1. The value of \(\left(\frac{4}{\sec ^2 \theta}+\frac{1}{1+\cot ^2 \theta}+3 \sin ^2 \theta\right)\) is ________

Solution: \(\frac{4}{\sec ^2 \theta}+\frac{1}{1+\cot ^2 \theta}+3 \sin ^2 \theta\)

= 4 cos² θ + \(\frac{1}{cosec^2 \theta}\) + 3sin² θ

= 4 cos² θ + sin² θ + 3 sin² θ = 4 cos² θ + 4 sin² θ

= 4 (cos² θ + sin² θ) = 4 x 1 =4

∴ Answer is 4.

Example 2. If sin (θ – 30°) = \(\frac{1}{2}\), then the value of cos θ is ______

Solution: sin (θ – 30°) = \(\frac{1}{2}\)

⇒ sin (θ – 30°) = sin 30°

⇒ θ – 30° = 30° ⇒ θ = 60°

cos θ = cos 60° = \(\frac{1}{2}\)

∴ Answer is \(\frac{1}{2}\)

Example 3. If cos² θ – sin² θ = \(\frac{1}{2}\), then the value of cos⁴ θ – sin⁴ θ is _______

Solution: cos⁴ θ- sin⁴ θ

= (cos² θ)² – (sin² θ)²

= (cos² θ + sin² θ) (cos² θ – sin² θ)

= 1 x \(\frac{1}{2}\) = \(\frac{1}{2}\)

∴ Answer is \(\frac{1}{2}\)

Wbbse Class 10 Trigonometry Notes

Example 4. The value of \(\left(\sin \frac{\pi}{3} \cos \frac{\pi}{6}+\cos \frac{\pi}{3} \sin \frac{\pi}{6}\right)\) is _____

Solution: sin\(\frac{\pi}{3}\)cos\(\frac{\pi}{6}\)+ cos\(\frac{\pi}{3}\)sin\(\frac{\pi}{6}\)

= sin\(\frac{180^{\circ}}{3}\)cos\(\frac{180^{\circ}}{6}\) + cos\(\frac{180^{\circ}}{3}\)sin\(\frac{180^{\circ}}{6}\)

= sin 60° cos 30° + cos 60° sin 30°

= \(\frac{\sqrt{3}}{2}\) x \(\frac{\sqrt{3}}{2}\) + \(\frac{1}{2}\) x \(\frac{1}{2}\) = \(\frac{3}{4}\) + \(\frac{1}{4}\) = 1

∴ Answer is 1.

Example 5. If a cos θ = 4 and a sec θ = 9, then the value of a is _______

Solution: a cos θ.a sec θ = 4 x 9

⇒ a² x 1 = 36

⇒ a = ± 6

∴ Answer is ± 6.

Angle Of Elevation And Depression Class 10 Solutions

Trigonometry Chapter 2 Trigonometric Ratios And Trigonometric Identities Short Answer Type Questions

Example 1. If r cos θ = 2√3, r sin θ = 2, and 0° < θ < 90°, then determine the value of both r and θ.

Solution: r cos θ = 2√3

r sin θ = 2

r² cos² θ + r² sin² θ = (2√3)² + (2)²

⇒ r² (cos² θ + sin² θ) = 12 + 4

⇒ r² x 1 = 16  ⇒ r = √16 = 4

r sin θ = 2

4 sin θ = 2

⇒ sin θ = \(\frac{2}{4}\) = \(\frac{1}{2}\)

⇒ sin θ = sin 30° ⇒ θ = 30°

∴ r = 2, θ = 30°

Example 2. If sin A + sin B = 2 where 0° ≤ A ≤ 90° and 0° ≤ B ≤ 90°, then find out the value of (cos A + cos B)

Solution: sin A + sin B = 2 = 1 + 1

⇔ sin A + sin B = sin 90° + sin 90°

⇔ sin A = sin 90°

⇔ A = 90°

⇔ Sin B = sin 90°

⇔ B = 90°

⇔ cos A + cos B = cos 90° + cos 90° = 0 + 0 = 0

Example 3. If 0° < θ < 90°, then calculate the least value of (9 tan² θ + 4 cot² θ).

Solution: 9 tan² θ +4 cot² θ

= (3 tan θ)² + (2 cot θ)²

= (3 tan θ – 2 cot θ)² + 2.3 tan θ.2 cot θ

= (3 tan θ- 2 cot θ)² + 12.1 [tan θ = 1/cot θ]

= (3 tan θ – 2 cot θ)² + 12

⇔ The least value of any perfect square of the expression is 0 (zero).

⇔ So, the least value of (3 tan θ – 2 cot θ) is zero.

∴ The least value of (9 tan² θ + 4 cot² θ) is 12.

Example 4. Calculate the value of (sin⁶ α + cos⁶ α + 3 sin²α + cos²α ).

Solution: sin⁶α + cos⁶α + 3 sin²α cos²α

= (sin²α)³ + (cos²α)³ + 3 sin²α cos²α

= (sin²α + cos²α)³ – 3.sin²α cos²α (sin²α + cos²α) + 3 sin²α cos²α

= (1)³ – 3 sin²α cos²α (1) + 3 sin²α cot²α

= 1-3 sin²α cos²α + 3 sin²α cos²α = 1

Example 5. If cosec² θ = 2 cot ² θ and 0° < θ < 90°, then determine the value of θ.

Solution: cosec² θ = 2 cot θ

⇒ 1 + cot² θ = 2 cot θ

⇒ cot² θ – 2 cot θ + 1 = 0

⇒ (cot θ – 1)² = 0  ⇒ cot θ – 1 = 0 ⇒ cot θ = 1

⇒ cot θ = cot 45° ⇒ θ = 45°

Class 10 Maths Trigonometry Important Questions

Example 6. If \(\frac{\cos \theta+\sin \theta}{\cos \theta-\sin \theta}=\frac{\sqrt{3}+1}{\sqrt{3}-1}\) then find the value of

Solution: \(\frac{\cos \theta+\sin \theta}{\cos \theta-\sin \theta}=\frac{\sqrt{3}+1}{\sqrt{3}-1}\)

⇒ \(\frac{\cos \theta+\sin \theta+\cos \theta-\sin \theta}{\cos \theta+\sin \theta-\cos \theta+\sin \theta}=\frac{\sqrt{3}+1+\sqrt{3}-1}{\sqrt{3}+1-\sqrt{3}+1}\) [By componendo-dividend process]

⇒ \(\frac{2 \cos \theta}{2 \sin \theta}=\frac{2 \sqrt{3}}{2}\)

⇒ \(\cot \theta=\sqrt{3}\)

⇒ cot θ = cot 30°

⇒ θ = 30°

Example 7. If \(\tan ^2 \frac{\pi}{4}-\sin ^2 \frac{\pi}{6}=x \sec ^2 \frac{\pi}{4} \cos ^2 \frac{\pi}{3}\) then find the value of x.

Solution: \(x \sec ^2 \frac{\pi}{4} \cos ^2 \frac{\pi}{3}=\tan ^2 \frac{\pi}{4}-\sin ^2 \frac{\pi}{6}\)

⇒ \(x \sec ^2 45^{\circ} \cos ^2 60^{\circ}=\tan ^2 45^{\circ}-\sin ^2 30^{\circ}\)

⇒ \(x \times(\sqrt{2})^2 \times\left(\frac{1}{2}\right)^2=(1)^2-\left(\frac{1}{2}\right)^2\)

⇒ x x 2 x \(\frac{1}{4}\) = 1 – \(\frac{1}{4}\)

⇒ \(\frac{x}{2}\) = \(\frac{3}{4}\)

⇒ x = \(\frac{3}{2}\)

Example 8. If tan θ + sin θ = a and tan θ – sin θ = b, then find the value of \(\frac{a^2-b^2}{\sqrt{a b}}\)

Solution: a² – b² = (tan θ + sin θ)² – (tan θ – sin θ)²

= 4 tan θ.sin θ

= \(\sqrt{\frac{\sin ^2 \theta}{\cos ^2 \theta}-\sin ^2 \theta}\)

= \(\sqrt{\sin ^2 \theta\left(\frac{1}{\cos ^2 \theta}-1\right)}=\sin \theta \sqrt{\frac{1-\cos ^2 \theta}{\cos ^2 \theta}}\)

= \(\sin \theta \cdot \sqrt{\frac{\sin ^2 \theta}{\cos ^2 \theta}}=\sin \theta \cdot \sqrt{\tan ^2 \theta}=\sin \theta \cdot \tan \theta\)

\(\frac{a^2-b^2}{\sqrt{a b}}=\frac{4 \sin \theta \tan \theta}{\sin \theta \cdot \tan \theta}=4\)

Class 10 Maths Trigonometry Important Questions

Example 9. If a sinθ + b cosθ = c, then find the value of (a cosθ – b sinθ).

Solution: a sinθ+ b cosθ = c

⇒ (a sinθ + bcosθ)² = c²

⇒ a² sin² θ + b² cos² θ + 2ab sinθcosθ= c²

⇒  a² (1 – cos² θ) + b² (1 – sin² θ) + 2ab si θ cosθ = c²

⇒ a² – a² cos² θ + b² – b² sin² θ + 2ab sinθ cosθ = c²

⇒ a² + b² – c² = a² cos² θ+ b² sin² θ- 2ab cosθ sinθ

⇒ a² + b² – c² = (acosθ – bsinθ)²

⇒ acosθ – bsinθ = ± \(\sqrt{a^2+b^2-c^2}\)

Example 10. If x = a sinθ and y = b tanθ, then find the value of \(\left(\frac{a^2}{x^2}-\frac{b^2}{y^2}\right)\).

Solution: a sinθ = x

⇒ \(\frac{a}{x}=\frac{1}{\sin \theta}={cosec} \theta\)

b tan θ = y

⇒ \(\frac{b}{y}=\frac{1}{\tan \theta}=\cot \theta\)

⇒ \(\frac{a^2}{x^2}-\frac{b^2}{y^2}={cosec}^2 \theta-\cot ^2 \theta=1\)

Example 11. If 0° < θ< 90° and 2 cos² θ + 3 sinθ = 3 then find the value of θ.

Solution: 2 cos² θ+ 3 sinθ = 3

⇒ 2 (1 – sin² θ) + 3 sinθ= 3

⇒ 2-2 sin² θ + 3 sinθ = 3

⇒ 2 sin² θ – 3 sinθ + 1 = 0

⇒ 2 sin² θ – 2 sinθ – sinθ + 1 = 0

⇒ 2 sinθ (sinθ – 1) – 1 (sinθ – 1) = 0

⇒ (sinθ – 1) (2 sinθ – 1) = 0

either sinθ – 1 =0

⇒ sinθ = 1

2 sinθ – 1 = 0

⇒ 2 sinθ = 1

⇒ sinθ = sin90°

⇒ sinθ = \(\frac{1}{2}\)

⇒ θ = 90°

⇒ sinθ = sin 30°

⇒ θ = 30°

As 0° < θ < 90°

∴ The value of θ is 30°

Example 12. If θ is positive acute angle then find the least value of (25 sec² θ + 49 cos² θ)

Solution: (25 sec² θ + 49 cos² θ)

= (5 secθ)² + (7 cosθ)²

= (5 secθ – 7 cosθ)² + 2.5 secθ 7 cosθ

=(5secθ -7cosθ)² +70secθ.\(\frac{1}{\sec \theta}\)

= (5 secθ – 7 cosθ)² + 70

(5 secθ – 7 cosθ)² ≥ 0

∴ Least value of (25 sec² θ + 49 cos² θ) is 70.

Example 13. If sinθ + sin² θ + sin³ θ = 1 then find the value of (cos⁶ θ- 4 cos⁴ θ + 8 cos² θ).

Solution: sinθ+ sin² θ+ sin³ θ = 1

⇒ sinθ + sin³ θ = 1 – sin² θ

⇒ sinθ (1 + sin² θ) = cos² θ

⇒ sin² θ (1 + sin² θ)² = cos⁴ θ [squaring both side]

⇒ (1 – cos² θ) (1 + 1 – cos² θ)² = cos⁴ θ

⇒ (1 -cos² θ) (2 – cos² θ)² = cos⁴ θ

⇒ (1- cos² θ) (4 – 4 cos² θ + cos⁴ θ) = cos⁴ θ

⇒ 4 – 4 cos² θ + cos⁴ θ – 4 cos² θ + 4 cos⁴ θ- cos⁶ θ = cos⁴ θ

⇒ cos⁶ θ – 4 cos⁴ θ + 8 cos² θ = 4

Class 10 Maths Trigonometry Chapter 2 Solutions

Example 14. In ΔABC each angle is a positive acute angle. If cos (B + C – A) = 0 and sin (C + A – B) = \(\frac{\sqrt{3}}{2}\), then find the value of A, B, and C.

Solution: cos (B + C – A) = 0

⇒ cos (B + C – A) = cos 90°

⇒ B + C – A = 90° ……(1)

sin (C + A – B) = \(\frac{\sqrt{3}}{2}\)

⇒ sin (C + A – B) = sin 60°

⇒ C + A- B = 60° ……..(2)

(1) + (2), we get

B + C- A + C + A- B= 90° + 60°

⇒ 2C = 150°  ⇒ C = 75°

From (2), 75° + A -B = 60°

⇒ A – B = – 15°……(3)

Again, In ΔABC,

A + B + C = 180°

A + B + 75° = 180°

⇒ A + B = 105°….(4)

A + B + A- B = 105°- 15°

⇒ 2A = 90°

⇒  A = 45°

∴ B = 105° – 45° = 60°.

Arithmetic Chapter 1 Simple Interest

⇔ In a simple interest system, interest is calculated only on the principal. The principle remains same for the entire time period.

⇔ Amount (A) = Principal (P) + Total interest (I)

⇔ If Rs P is the principal, r% is the rate of interest per annum and t is the number of years, then

⇔ \(\text { S. I. }(I)=\text { Rs. } \frac{prt}{100}\)

⇔ Amount = Rs.\(\left(p+\frac{p r t}{100}\right)\) = P

⇔ Time = \(\left(\frac{\text { Total interest }}{\text { Interest on the principal for } 1 \text { year }}\right) \text { years }\)

Read and Learn More WBBSE Solutions for Class 10 Maths

Arithmetic Chapter 1 Simple Interest True Or False

Example 1. A man takes a loan is called a debtor.

Solution: True

Example 2. If the principal and the rate of simple interest in percent per annum be constants, then the total interest and the time are in inverse relation.

Solution: False

Arithmetic Progression Class 10 Solutions

Example 3. If a certain sum of money doubles itself in 10 years, ten r = 20% per annum.

Solution: False

Example 4. A borrowed Rs. P at 10% per annum simple interest the amount will be at the end of 10 years will be 2P.

Solution: False

Example 5. If the interest on Rs. x for t years is Rs. y, then rate % is \(\frac{100 y}{x t}\)%

Solution: True

Arithmetic Chapter 1 Simple Interest Fill In The Blanks

Example 1. A man who is given a loan is called _______.

Solution: Creditor

Example 2. The amount of ₹ 2P in t years, at the rate of simple interest of \(\frac{r}{2}\) % per ainiuam is ₹ (2P + _____)

Solution: \(\frac{P r t}{a}\)

Example 3. The ratio of the principal and the amount (P. + S.I) in 1 year is 8 : 9, r% = ________

Solution: 12 \(\frac{1}{2}\)

Class 10 Arithmetic Chapter 1 Solved Examples

Example 4. The simple interest at the rate of x% p.a. for x years, will be Rs. x on a sum of _______

Solution: Rs. \(\frac{100}{n}\)

Example 5. The simple interest on Rs. 500 for 6 years at 5% per annum is___________

Solution: Rs. 150

Arithmetic Chapter 1 Simple Interest Short Answer Type Questions

Example 1. By what principal at the rate of 6\(\frac{1}{4}\) % per annum for 1 day will be Re 1?

Solution: Simple interest = \(\frac{P R T}{100}\)

or, P = 5840

∴ principal = Rs. 5840

Example 2. The rate of simple interest is reduced to 4% to 3\(\frac{3}{4}\)% and for this, Amal Babu’s annual income decreases by ₹ 60. Find Amal Babu’s principal.

Solution: \(P \times\left(\frac{4}{100}-\frac{15}{4 \times 100}\right)\) = Rs.60

or, \(P \times \frac{1}{4 \times 100}\) = Rs. 60

or, P = 24000

Principal = Rs. 24000

Arithmetic Progression Formulas Class 10

Example 3. What is the rate of simple interest when the interest of some money in 4 years, will be \(\frac{8}{25}\) part of the principal let us determine it.

Solution:

R = 8

Rate = 8% per annum.

Important results:

1. Simple interest = \(\frac{P T R}{100}\)

2. \(R=\frac{S. I \times 100}{P \times T}\)

3. \(T=\frac{S. I \times 100}{P \times R}\)

4. A = P + S.I

5. A = \(\mathrm{P}\left(1+\frac{\mathrm{T} \times \mathrm{R}}{100}\right)\)

6. P = \(\frac{\mathrm{A} \times 100}{100+\mathrm{TR}}\)

Example 4. If rate to interest is R₁% for T₁ years, R₂% for next T₂ years, R₃% for next T₃ years, and so on, and total interest is simple interest then P is

Solution: \(P=\frac{S . I \times 100}{R_1 T+R_2 T_2+R_3 T_3+\cdots}\)

Class 10 Maths Arithmetic Important Questions

Example 5. When sum of money becomes n times in T years, then rate of interest is given by

Solution: \(\mathrm{R}=\frac{100(n-1)}{T} \% \text { per annum }\)

Example 6. If a sum of amounts to ₹ A₁ in T₁ years and ₹ A₂ in T₂ years at simple interest, then rate of interest is given by

Solution: \(R=\frac{100\left(A_2-A_1\right)}{A_1 T_2-A_2 T_1}\)

Example 7. If a sum of amounts to ₹ A₁ at R₁% per annum and ₹ A₁ at R₁% per annum for same duration, then

Solution: \(T=\frac{100\left(A_2-A_1\right)}{A_1 R_2-A_2 R_1}\)

Algebra Chapter 2 Ratio And Proportion

⇔ How many times or division of another same quantity in comparison to a quantity is called ratio.

⇒ \(a: b=\frac{a}{b}=\frac{a k}{b k}=a k: b k,(k \neq 0)\)

⇒ or, \(\quad a: b=\frac{\frac{a}{k}}{\frac{b}{k}}=\frac{a}{k}: \frac{b}{k}(k \neq 0)\)

⇒ That means a ratio does not alter if its first and 2nd terms are multiplied or divided by the same nonzero number.

⇒ The value of ratio of two real numbers x and y (y≠ 0) is x: y or \(\frac{x}{y}\), this x: y is read as ‘x is to y’, x is called the antecedent and y is called consequent of the ratio.

Class 10 Maths Algebra Chapter 2 Solutions

⇒ If \(\frac{x}{y}\) > 1 then it is called a ratio of greater inequality and if \(\frac{x}{y}\) < 1, the ratio is called the ratio of less inequality.

⇒ If x = y then the ratio is called the ratio of equality.

⇒ y: x is the inverse ratio of x: y.

Read and Learn More WBBSE Solutions for Class 10 Maths

⇒ From two or more given ratios, if we take antecedent as a product of antecedents of the given ratios and consequent as a product of consequents of the given ratios, then the ratio is called mixed or compound ratio.

⇒ The compound ratio of a: b, c : d, and e: f is ace: bdf.

Proportion:

If four real numbers are such that the ratio of the first two is equal to ratio of the last two, then the four numbers in that order are said to be proportional or said to be in proportion.

⇒ If four real numbers p, q, r, s (q ≠ 0, s ≠ 0) be in proportion, we write p: q : : r: s, where p, q are called extreme terms; q, r are called middle terms and s is called the fourth term.

⇒ If a: b : : b: c then a, b, c are in continued proportion, and b is called the mean proportional of a & c.

⇒ Here b² = ac or b = ±√ac

Properties of proportion:

1. If a: b : : c : d then a: c : : b : d.

⇒ This property is called alternendo.

2. If a: b : : c : d then b: a : : d: c

⇒ This property is called invertendo.

3. If a : b : : c : d then (a + b) : b : : (c + d) : d

⇒ This property is called componendo.

4. If (a: b : : c : d then (a – b): b : : (c – d) : d.

⇒ This property is called Dividendo.

5. If a: b :: c : d then \(\frac{a + b}{a – b}\) : : \(\frac{c + d}{c – d}\)

⇒ This property is culled Componendo And Dividendo.

6. If a: b : : c : d then each ratio = \(\frac{a + c}{b + d}\)

⇒ This property is called Addendo.

Quadratic Equations Class 10 Solutions

Algebra Chapter 2 Ratio And Proportion True Or False

Example 1. The mean proportional of 4 and 16 is ±.8.

Solution: True

Example 2. In any ratio of greater inequality antecedent > consequent.

Solution: True

Example 3. In any ratio of less inequality antecedent = consequent.

Solution: False

Example 4. If product of three positive continued proportional number is 27, then their mean proportion is 9.

Solution: False

Example 5. Mixed ratio of \(x: \frac{y z}{x}, y: \frac{z x}{y} \text { and } z: \frac{x y}{z}\) is 1: 1.

Solution: True

Class 10 Algebra Chapter 2 Solved Examples

Example 6. The compound ratio of ab: c², bc: a^2, and ca: b² is 1: 1.

Solution: True

Example 7. x³y, x²y²y, and xy² are in continued proportion.

Solution: True

Example 8. Fourth proportional of 2, 6, and 8 is 16.

Solution: False

Example 9. If x, y, and z are in continued proportion then xy = z².

Solution: False

Example 10. If x : y = 5 : 7 then \(\frac{1}{x^2}: \frac{1}{y^2}\) = 49 : 25

Solution: True

Algebra Chapter 2 Ratio And Proportion Fill In The Blanks

Example 1. If the product of three positive continued proportional number is 64, then their mean proportional is ______

Solution: 4

Example 2. If a : 2 = b : 5 = c : 8 then 50% of a = 20% of b = ________% of c.

Solution: 12\(\frac{1}{2}\)

Example 3. The mean proportional of (x – 2) and (x- 3) is x, then value of x is _______

Solution: \(\frac{6}{5}\)

Example 4. If the value of a ratio is greater than 1, then the ratio is called ______

Solution: Greater inequality

Quadratic Equations Formulas Class 10

Example 5. If the value of a ratio is less than 1, then the ratio is called _______

Solution: Less inequality

Example 6. The inverse ratio of x : 3 is ______

Solution: 3: 2

Example 7. 5: 5 is called the ratio of ______

Solution: Equality

Example 8. If x: 2x : : 3: y then y = ______

Solution: 6

Example 9. If a, b, c, and d are in proportion then ad = ______

Solution: bc

Class 10 Maths Algebra Important Questions

Example 10. Third proportion of Rs 4 and Rs 12 is _______

Solution: Rs. 36

Example 11. If a, b, and c are in continued proportion then b is called the _______ and c is called the ______

Solution: Mean proportion, third proportion

Example 12. If A : B = 5 : 6, B:C = 6:7, C:D = 7:8, D:E = 8:5 then A : E = ______

Solution: 1: 1

Algebra Chapter 2 Ratio And Proportion Short Answer Type Questions

Example 1. If \(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}=\frac{2 a-3 b+4 c}{p}\), find p.

Solution: Let \(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}=k \quad(\neq 0)\)

∴ \(\frac{2 a-3 b+4 c}{p}=\frac{2 \cdot 2 k-3 \cdot 3 k+4 \cdot 4 k}{p}=k\)

⇒ or, \(\frac{11 k}{p}=k\) ∴ p=11

Example 2. If \(\frac{3 x-5 y}{3 x+5 y}=\frac{1}{2}\) find the value of \(\frac{3 x^2-5 y^2}{3 x^2+5 y^2}\)

Solution: \(\frac{3 x-5 y+3 x+5 y}{3 x-5 y-3 x-5 y}=\frac{1+2}{1-2}\)

⇒ or, \(\frac{6 x}{-10 y}=\frac{3}{-1}\) or, \(\frac{3 x}{5 y}=3\) or, x = 5y

⇒ Now, \(\frac{3 x^2}{5 y^2}=\frac{3 \cdot 25 y^2}{5 y^2}=15\)

⇒ ∴ \(\frac{3 x^2-5 y^2}{3 x^2+5 y^2}=\frac{15-1}{15+1}=\frac{14}{16}=\frac{7}{8}\)

Class 10 Maths Algebra Important Questions

Example 3. If a : A = 3 : 4, x : y = 5 : 7 then find the value of (3ax – by) : (4by – 7ax)

Solution: \(\frac{a}{b} \times \frac{x}{y}=\frac{3}{4} \times \frac{5}{7}\)

⇒ or, \(\frac{a x}{b y}=\frac{15}{28}\)

⇒ ∴ \(\frac{3 a x-b y}{4 b y-7 a x}=\frac{3 \times \frac{15 b y}{28}-b y}{4 b y-7 \times \frac{15 b y}{28}}\)

= \(\frac{4\left(\frac{+17 b y}{28}\right)}{b y}=\frac{17}{7}\)

Example 4. If x, 12, y, and 27 are in continued proportion, find the positive value of x & y.

Solution: y² = 12 x 27

⇒ or, y = \(\sqrt{12 \times 27}\) = 18

⇒ Now, xy = 12²

⇒ or, x = \(\frac{144}{18}\) = 8

Example 5. If a: b = 3: 2, b: c = 3: 2, then find the value of (a + b) : (b + c).

Solution: a: b = 3: 2 = 9: 6

⇒ b: c = 3: 2 = 6: 4

⇒ ∴ a : b : c = 9 : 6 : 4

⇒ Let, a, b, c be 9k, 6k, 4k (k ≠ 0)

⇒ \(\frac{a+b}{b+c}=\frac{9 k+6 k}{6 k+4 k}=\frac{15}{10}=\frac{3}{2}\)

Class 10 Maths Algebra Important Questions

Example 6. If a, b, c, d are in continued proportion, then find the value of \(\frac{a d c(a+b+c)}{a b+b c+c a}\)

Solution: Let \(\frac{a}{b}\) = \(\frac{b}{c}\) = \(\frac{c}{d}\) r (≠0)

⇒ a = br, b = cr, c = dr

⇒ ∴ b = dr², a = dr².

⇒ \(\frac{a b c(a+b+c)}{a b+b c+c a}=\frac{d r^3 \cdot d \cdot d r\left(d r^3+d r^2+d r\right)}{d r^3 \cdot d r^2+d r^2 \cdot d r+d r \cdot d r^3}\)

= \(\frac{d^3 r^4 \cdot d r\left(r^2+r+1\right)}{d^2 r^3\left(r^2+r+1\right)}\) = \(d^2 r^2=c^2\)

Example 7. If x: y = 5: 6 then find the value of \(\frac{3 x+4 y}{4 x+3 y}\)

Solution: \(\frac{x}{y}=\frac{5}{6}\)

⇒ Now, \(\frac{3 x+4 y}{4 x+3 y}=\frac{y\left(3 \frac{x}{y}+4\right)}{y\left(4 \frac{x}{y}+3\right)}\)

= \(\frac{5+8}{2} \times \frac{3}{19}=\frac{39}{38}\)

Example 8. What should be subtracted from each term of 4 : 9 to make the ratio equal to 8 : 7 = ?

Solution: Let the required term be x

⇒ \(\frac{4-x}{9-x}=\frac{8}{7}\)

⇒ or, 28 – 7x = 72 – 8x

⇒ or, x = 44

Example 9. If 7 + x, 11 + x, and 19 + x are in continued proportion, then find the value of x.

Solution: (7 + x) (19 + x) = (11 + x)²

⇒ or, 133 + 26x + x² = 121 + x² + 22x

⇒ or, 4x = – 12,

⇒ or, x = -3

The value of x = -3

Class 10 Maths Board Exam Solutions

Example 10. If \(\frac{x}{l m-n^2}=\frac{y}{m n-l^2}=\frac{z}{n l-m^2}\) then find the value of lx + my + xz.

Solution: Let \(\frac{x}{l m-n^2}=\frac{y}{m n-l^2}=\frac{z}{n l-m^2}=k(\neq 0)\)

∴ x = k (lm – n²); y = k(mn – l²); z = k(nl – m²)

∴ lx + my + xz

= lk (lm – n²) + mk (mn – l²) + nk (nl – m²)

= k (l²m- ln² + m²n – ml² + n²l – m²n)

= k.0 = 0.

The value of lx + my + xz = 0.

Algebra Chapter 1 Quadratic Equations With One Variable

1. If the factors of a quadratic equation ax² + bx + c = 0, (a ≠ 0) are (x – α) and (x – β) respectively then ax² + bx + c = 0 and (x- α)(x- β) are equivalent.

⇒ Here α, β are the roots of that quadratic equation.

2. Sreedhar Acharya’s method to find the roots of ay² + by + c = 0, (a ≠ 0) is \(x=\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)

3. If α, β are the roots of the quadratic equation ax² + bx + c = 0, (a ≠ 0) then

⇒  \(\alpha+\beta=-\frac{\text { co-efficient of } x}{\text { co-efficient of } x^2}=-\frac{b}{a}\) and

Read and Learn More WBBSE Solutions for Class 10 Maths

⇒  \(\alpha \beta=\frac{\text { co-efficient of } x^{\circ}}{\text { co-efficient of } x^2}=\frac{c}{a}\)

4. If α, β are the roots of a quadratic equation then the equation will be x² – (α + β) x + αβ = 0

5. Roots of ax² + bx + c = 0, (a ≠ 0) are

1. Real and unequal if b² – 4ac > 0
2. Real and equal if b² – 4ac = 0
3. Imaginary if b² – 4ac < 0

6. If one root of a quadratic equation is a + √b (√b is a pure surd) then the other root is the conjugate of a + √b, i.e., a – √b

Class 10 Maths Algebra Chapter 1 Solutions

Roots under particular conditions:

For quadratic equation ax² + bx + c = 0

1. If b = 0, Roots are real/imaginary as (c < 0 or c > 0) and equal in magnitude but of opposite sign.

2. If c = 0 ⇒ one root is zero, other is \(\frac{b}{a}\).

3. If b = c = 0 ⇒ Both roots are zero.

4. If a = c ⇒ Roots are reciprocal to each other.

5. If a > 0, c < 0; a < 0, c > 0

Roots are of opposite sign.

6. If a > 0, b > 0, c > 0; a < 0, b < 0, c < 0

⇒  Both roots are negative, provided D ≥ 0.

7. If a > 0, b < 0, c > 0; a < 0, b > 0, c < 0

⇒  Both roots are positive, provided D ≤ 0.

8. If sign of a = sign of b ≠ sign of c ⇒ greater root in magnitude is negative.

9. If sign of b = sign of c ≠ sign of a ⇒ greater root in magnitude is positive.

10. If a + b + c = 0 => one root is 1 and the second root is \(\frac{c}{a}\).

Algebra Chapter 1 Quadratic Equations With One Variable True Or False

Example 1. The two roots of the equation x² – 5x + 6 = 0 are real.

Solution: True

Example 2. The two roots of the equation 2x² – x – 6 = 0 are not real.

Solution: False

Example 3. One root of the equation ax² + bx + c = 0, a ≠ 0 is zero when c = 0.

Solution: True

Linear Equations Class 10 Solutions

Example 4. The roots ot the equation ax² + bx + c = 0 are reciprocal to one another when a = b.

Solution: False

Example 5. If the signs of a and c are opposite to that of b then both roots of the equation ax² + bx + c = 0, a (≠0) are positive.

Solution: True

Example 6. The roots ot the equation ax² + bx + c = 0, (a ≠ 0) are equal in magnitude and opposite in signs when c = 0.

Solution: False

Example 7. If b = c = 0, then both roots of the equation ax² + bx + c = 0, (a ≠ 0) are positive.

Solution: False

Class 10 Algebra Chapter 1 Solved Examples

Example 8. The roots of the equation ax² + bx + c = 0, (a ≠ 0) are equal when b² – 4ac > 0.

Solution: False

Example 9. Sum of the roots of 3x²– 5x + 7 = 0 is – 5.

Solution: False

Example 10. Product of the roots of 2x² – 3x + 7 = 0 is \(\frac{-7}{2}\)

Solution: False

Algebra Chapter 1 Quadratic Equations With One Variable Fill In The Blanks

Example 1. The ratio of the sum and the product of two roots of the equation 7x²– 12x + 18 = 0 _______

Solution: 2: 3

Example 2. If two roots of the equation ax² + bx + c = 0, (a ≠ 0) are reciprocal to each other, then c = _______

Solution: a

Example 3. If two roots of the equation ax² + bx + c = 0, (a ≠ 0) are reciprocal to each other and opposite(negative), then a + c = _______

Solution: 0

Example 4. Sum of the roots of 2x² – 6x + 9 = 0 is _______

Solution: 3

Example 5. If the roots of ax² – bx + c = 0, (a ≠ 0) are equal then c = _______

Solution: \(\frac{b^2}{4 a}\)

Wbbse Class 10 Algebra Notes

Example 6. If the roots of the equation 3x² + 8x + 2 = 0 are α, β the \(\frac{1}{\alpha}+\frac{1}{\beta}\) = _____

Solution: -4

Example 7. Roots of (k + 1) x²+ 2kx + (k + 2) = 0, (k ≠ – 1) are equal in magnitude but opposite in sign then k = _____

Solution: 0

Example 8. If the roots of the equation ax² + bx + c = 0, (a ≠ 0) are reciprocal to each other then c = _______

Solution: a

Example 9. If the product of the roots x²– 3x + k = 0 is -2, then k = _____

Solution: 8

Example 10. Sum of the roots of 3x² – 5 = 0 is ______

Solution: 0

Linear Equations Formulas Class 10

Algebra Chapter 1 Quadratic Equations With One Variable Short Answer Type Questions

Example 1. One root of equation 3x² – 5x + c = 0 is 2, find its other root.

Solution: Let the other roots be α

∴ \(\alpha+2=\frac{5}{3} \Rightarrow \alpha=\frac{5}{3}-2=-\frac{1}{3}\)

Example 2. The product of the roots of the equation 3x²+ mn – (2m + 3) = 0 is 5, find m.

Solution: \(-\frac{(2 m+3)}{3}=5\)

⇒  or, – (2m + 3) = 15 or, m = – 9.

Example 3. Form a quadratic equation with rational coefficients where one root is 4 + √7

Solution: Other root is 4 – √7

⇒  Equation is x² -(4 + √7 +4 – √7)+ (4 + √7)(4- √7) = 0

⇒  or, x² – 8x + (16 – 7) = 0, or, x² – 8x + 9 = 0

Example 4. If α, β are the roots of x (x – 3) = 4, find the value of α² + β².

Solution: x² – 3x- 4 = 0

⇒ α + β = 3, αβ = – 4

⇒ α² + β² = (α + β)² – 22β

= 3² -2(-4) = 9 + 8= 17

Class 10 Maths Algebra Important Questions

Example 5. Let us write the quadratic equation if sum of its roots is 14 and product is 24.

Solution: Required equation is x² – 14x + 24 = 0

Example 6. If the sum and the product of two roots of the equation kx² + 2x + 3k = 0, (k ≠ 0) are equal, let us write the value of k.

Solution: \(-\frac{2}{k}=\frac{3 k}{k}\) (k ≠ 0)

⇒ or, k = \(\frac{-2}{3}\)

Example 7. If two roots of x² – 22x + 105 = 0 are α, β, find the value of α – β.

Solution: α + β = 22, αβ = 105

⇒ (α – β)² = (α + β)² – 4αβ

= (22)² – 4 x 105 = 484 – 420 = 64

∴ α – β = ± 8

Example 8. If the sum of two roots of x² – x = k (2x – 1) is zero, find the value of k.

Solution: x² – x = 2kx – k

⇒ or, x² – x(2k + 1) + k = 0

⇒ sum of the roots = 0 or, \(\frac{2 k+1}{1}\) = 0 ⇒ k = \(-\frac{1}{2}\)

Example 9. If one of the roots of the two equations x2 + bx + 12 = 0 and x2 + bx + q = 0 is 2, find the value of q.

Solution: (2)² + b.2 + 12 = 0

⇒ or, 2b = – 16  ∴ b = -16

⇒ Now, (2)² + b.2 + q = 0

⇒ or, 4 + (- 8) 2 + q = 0

⇒ or, q = – 4 + 16 = 12

Class 10 Maths Board Exam solutions

Example 10. If one root of x² – 2x + c = 0 is thrice of another root, then find the value of c.

Solution: Let the roots be α, 3β

⇒ a + 3α = 2

⇒ α, 3α = c

⇒ α = \(\frac{2}{4}\) = \(\frac{1}{2}\)

⇒ or, \(3\left(\frac{1}{2}\right)^2=c\)

⇒ or, c =\(\frac{3}{4}\)

Arithmetic Chapter 3 Partnership Business

⇔ If two or more persons start a business with their respective capitals, then the business is called a Partnership business.

⇔ The profit or loss in the business is divided on the basis of the ratio of their investment if otherwise is not started.

It is of two kinds:

⇔ Simple partnership: When the capital of the partners are invested for the same period of time.

⇔ Compound partnership: If the capital of the partners is invested for different periods of time. Here at first, we calculate the equivalent capital (with respect to time) of each partner.

⇔ We calculate the equivalent capitals in respect of 1 month. The individual capital is multiplied by the no. of months of the capital invested.

Read and Learn More WBBSE Solutions for Class 10 Maths

Arithmetic Chapter 3 Partnership Business True Or False

Example 1. At least 3 persons are needed in a partnership business.

Solution: False

Example 2. Ratio of capital of Raju and Ashif in a business is 5: 4 and if Raju gets profit share of ₹ 80 of total profit. Ashif will get a profit share of ₹ 100.

Solution: False

Class 10 Maths Arithmetic Chapter 3 Solutions

Example 3. If A and B invest an equal amount of money for 9 months and 8 months respectively, then the profit will be distributed in the ratio 9:8.

Solution: True

Example 4. The ratio of capital of three partners in a partnership business is 2 : 3 : 3 and the ratio of time is 3 : 2 : 2, then each will get equal share of profit.

Solution: True

Example 5. If the ratio of capital of A, B, C is \(\frac{1}{6}\): \(\frac{1}{5}\): \(\frac{1}{4}\), then the profit will be distributed in the ratio of 4:5:6.

Solution: True

Example 6. At least two partners are needed for a partnership business.

Solution: False

Example 7. Honerrary allowance is distributed after the profit is shared.

Solution: True

Class 10 Maths Arithmetic Chapter 3 Solutions

Example 8. In a simple partnership, business capitals are invested for the same period of time.

Solution: True

Example 9. In a compound partnership business capitals are invested for the different period of time.

Solution: False

Example 10. To find equivalent capital, investment is added with respect to the time.

Solution: False

Example 11. For a compound partnership business, at first we calculate the ratio of their initial capitals.

Solution: True

Compound Interest Class 10 Solutions

Arithmetic Chapter 3 Partnership Business Fill In The Blanks

Example 1. Partnership business is ______ type.

Solution: Two

Example 2. Without any other conditions in partnership business if the capitals of all partners are invested for the same time, then such a business is called _______

Solution: Simple

Example 3. Without any other conditions in partnership business, if the capitals of all partners are invested for different time periods, then such a business is called _________

Solution: Compound

Example 4. In a partnership business, share of profit is distributed in _______ ways.

Solution: 3

Class 10 Arithmetic Chapter 3 Solved Examples

Example 5. When the investment of the partners in involved in a business for different time period of time then it is called a ______ business.

Solution: Joint partnership

Example 6. A and B’s shares in a business are equal, but the profit is distributed in the ratio of 4: 5. The business was a _____ partnership.

Solution: Joint

Example 7. The profit is shared only after the dissbursement of _______

Solution: Honorrary

Example 8. The business partners collect the total amount of capital by investing equally or at a _________ ratio.

Solution: Unanimous

Wbbse Class 10 Arithmetic Notes

Arithmetic Chapter 3 Partnership Business Short Answer Type Questions

Example 1. In a partnership business, the ratio of capitals of Samir, Idrish, and Antony are as \(\frac{1}{6}\): \(\frac{1}{5}\): \(\frac{1}{4}\). If they make a profit of ₹ 3700 at the end of the year. Let us write by calculating profit share of Antony.

Solution: Ratio = \(\frac{1}{6}\): \(\frac{1}{5}\): \(\frac{1}{4}\) = 10: 12: 15

Share of Antory = ₹ 3700 x \(\frac{15}{37}\) = ₹ 1500

∴ Profit share of Antony is ₹ 15000

Example 2. If in a partnership business the ratio of capitals of Pritha and Rabeya is 2 : 3 and the ratio of Rabeya and Jesmin is 4 : 5. Let us write by calculating the ratio of capitals of Pritha Rabeya and Jesmin.

Solution: Ratio of capitals of Pritha and Rabeya = 2 : 3 = 8 = 12

Ratio of capitals of Rabeya and Jesmin = 4 : 5 = 12 : 15

Required ratio = 8: 12: 15

∴ The ratio of capitals of Pritha, Rabeya, and Jesmin is 18: 12: 15

Example 3. The total profit is ₹ 1500 in a partnership business of two persons. If the capital of Rajib is ₹ 600 and profit is ₹ 900, let us calculate how much was the capital of Abtab.

Solution: Profit of Abtab = ₹ (1500 – 700) = ₹ 600

∴ Rohit of capitals = Ratio of profit

6000 : x = 900 : 600 or, x = 4000

Capital of Abtab = ₹ 4000

∴ The capital of Abatab is ₹ 4000

Example 4. Ratio of capitals of 3 persons is 3: 8: 5 and the profit of 1st is 7 60 less of the 3rd. Calculate the total profit in this business.

Solution: Clearly profit is ₹ 3x, ₹ 8x, ₹ 5x (x is a ratio constant, x > y)

∴ 5x- 60 = 3x or, 2x = 60, or, x = 30

∴ Total profit = ₹ 16x = ₹ 16 x 30 = ₹ 480.

Compound Interest Formulas Class 10

Example 5. Jayanti, Ajit and Kunal started partnership business investing ₹ 15000. At the end of the year. Jayanti, Ajit and Kunal received ₹ 800, ₹1000, ₹1200 respectively on profit share. Let us calculate the amount of Jayanta’s capital that was invested in the business.

Solution: Ratio of profit = 800 : 1000 : 1200 = 8 : 10 : 12

= 4:5:6 = Ratio of capitals

Jayanti’s capital =

∴ The amount of Jayanta’s capital that wat invested in the business is ₹ 4000

Example 6. Shyam invested ₹ 2000 for 9 months and Kunal invests 7 1500 for few months in a business. If the total profit be ₹ 484 and Shyam gets ₹ 264 as is share of profit. Then calculate the time for which Kunul’s capital was invested.

Solution: Ratio of equivalent capitals = (2000 x 9) : (1500x)

= (20 x 9) : 15x = 12 : x

∴ x = 10

∴ Time required 10 months.

∴ The time for which Kunal’s capital was invested is 10 months.

Example 7. Share of capitals of A, B, and C in a business is \(\frac{1}{6}\): \(\frac{1}{5}\): \(\frac{1}{4}\) At the end of the year profit is Rs. 37000. Final profit share of C.

Solution: \(\frac{1}{6}\): \(\frac{1}{5}\): \(\frac{1}{4}\) = 10: 12: 15

Profit of C = ₹ 37000 x \(\frac{15}{37}\) = ₹ 1500

∴ Final profit share of C is ₹ 1500.

Class 10 Maths Arithmetic Important Questions

Example 8. Selim, Joy, and John started a partnership business with capitals ₹ 5000, ₹ 4500, ₹ 7000 respectively. If the profit is ₹ 11550. Find the profit share of Joy.

Solution: Ratio of capitals = 5000 : 4500 : 7000 = 50 : 45 : 70 = 10 : 9 : 14

Profit of Joy =

= Rs. 3150.

∴ The profit share of Joy is ₹ 3150.

Algebra Chapter 4 Variation

⇔ If the variable x and y are related to each other in such a way that \(\frac{x}{y}\) = k (now zero constant), it is called that x and y are in direct variation and non-zero constant is said to be variation constant, x and y are in Direct variation and it can be written as x y and now zero constant is said to be variation constant.

⇒ If two variables x and y are related to each other in such a way that xy = k (non-zero constant), then it is said x and y are in inverse variation and written as x \(\frac{1}{y}\) and non zero constant is said to be variation constant.

⇒ If a variable in direct variation with the product of two or more variables, the first variable is said to be in joint variation with other variables.

Theorem on joint variation: If three variables x, y, z be such that x ∝ y when z is constant, x ∝ z when y is constant, then x ∝ yz when y and z both vary.

Read and Learn More WBBSE Solutions for Class 10 Maths

Algebra Chapter 4 Variation True Or False

Example 1. y ∝ \(\frac{1}{x}\) then \(\frac{y}{x}\) = non zero constant.

Solution: False

Example 2. If x ∝ z and y ∝ z then xy ∝ z.

Solution: True

Class 10 Maths Algebra Chapter 4 Solutions

Example 3. If x ∝ y² and y = 2a when x = a then y² = 4ax.

Solution: True

Example 4. If \(\frac{x}{y}\) ∝ z, \(\frac{y}{z}\) ∝ x \(\frac{z}{x}\) ∝ y then xyz = 1.

Solution: False

Example 5. If x ∝ y, y ∝ z then x μ z.

Solution: True

Example 6. If x ∝ \(\frac{1}{y}\), y ∝ \(\frac{1}{z}\) then x ∝ \(\frac{1}{z}\)

Solution: False

Example 7. If A² ∝ BC, B² ∝ CA, C² ∝ AB then the product of three variations constant = 1.

Solution: True

Rational Expressions Class 10 Solutions

Example 8. If x ∝ \(\frac{1}{z}\) when y is constant and x ∝ y when z is constant then x ∝ \(\frac{y}{z}\) then both y and z vary.

Solution: True

Example 9. If x ∝ y then x + y ∝ \(\frac{1}{x-y}\)

Solution: False

Example 10. If x ∝ y then xⁿ ∝ yⁿ.

Solution: True

Example 11. If A² + B² ∝ A² – B² then A ∝ \(\frac{1}{B}\)

Solution: False

Example 12. If \(\frac{x}{y}\) ∝ x + y and \(\frac{y}{x}\) ∝ x-y then x² – y = constant.

Solution: True

Class 10 Algebra Chapter 4 Solved Examples

Algebra Chapter 4 Variation Fill In The Blanks

Example 1. If x ∝ \(\frac{1}{y}\) and y ∝ \(\frac{1}{z}\) then x  ∝ _____

Solution: z

Example 2. If x ∝ y, xⁿ ∝ ______

Solution: yⁿ

Example 3. If x ∝ y and x ∝ z then (y + z) ∝ _____

Solution: x

Example 4. If \(\frac{x}{y}\) constant, then x and y are in ______ variation.

Solution: Direct

Example 5. If xy = constant then x and y are in _______ variation.

Solution: Inverse

Example 6. If a variable is in direct variation with the product of two or more variables, the first variable is said to be in _______ variation with the other variables.

Solution: Joint

Simplifying Rational Expressions Class 10

Example 7. If V = R\(\frac{T}{P}\) (R = constant) in this relation we can say that V is in _______ variation with T and \(\frac{1}{P}\).

Solution: Joint

Example 8. If \(\frac{x}{y}\) ∝ x + y and \(\frac{y}{x}\) ∝ x -y then x² – y² = _______

Solution: Constant

Example 9. If x² ∝ yz, y² ∝ zx, z² ∝ xy then the product of the three non-zero variation constants is _________

Solution: 1

Example 10. If x + y ∝ x- y then x _______

Solution: y

Simplifying Rational Expressions Class 10

Algebra Chapter 4 Variation Short Answer Type Questions

Example 1. If x ∝ y² and y = 2a when x = a. Find the relation between x and y.

Solution: x = ky² [x is a non-zero variation constant.]

∴ a = k (2a)²

or, k = \(\frac{1}{4a}\)

x= \(\frac{1}{4a}\)y²

∴ y² = 4ax.

Example 2. If x ∝ y, y ∝ z and z ∝ x, find the product of three non-zero constants.

Solution: x = k₁y, y = k₂z, z = k₃x [k₁, k₂, k₃ are three non zero constants]

∴ xyz = k₁k₂k₃ xyz

∴ k₁k₂k₃ = 1

∴ Required product is 1.

Example 3. If x ∝ \(\frac{1}{y}\), y ∝ \(\frac{1}{z}\) find if there be any relation direct or inverse variation between x and z.

Solution: \(x=\frac{k_1}{y}, y=\frac{k_2}{z}\)

⇒ [k₁, k₂ are non-zero constants]

∴ x = \(\frac{k_1}{\frac{k_2}{z}} \quad \text { or, } \quad x=\frac{k_1}{k_2} z\)

∴ x ∝ z [\(\frac{k_1}{k_2}\) constant]

⇒ There is a direct variation.

Example 4. If x ∝ yz and y ∝ zx, show that z is a nonzero constant.

Solution: x = k₁yz, y = k₂zx [k₁k₂ are non-zero constant.]

⇒ or, xy = k₁k₂ yz²x or, 1 = k₁k₂z²

∴ \(z= \pm \sqrt{\frac{1}{k_1 k_2}}\) = non zero constant.

Class 10 Maths Algebra Important Questions

Example 5. If b ∝ a³ and an increases ratio of 2 : 3, find what ratio b will increase.

Solution: b = ka³ [k is a non zero variation constant]

⇒ b₁: b₂ = 8: 27.

Example 6. If \(\left(a x+\frac{b}{y}\right) \propto\left(c x+\frac{d}{y}\right)\) then show that xy = constant, (where a, b, c, d constant).

Solution: \(\left(a x+\frac{b}{y}\right)\) = k \(\left(c x+\frac{d}{y}\right)\)

⇒ or, x(a-kc) = (kd-b)\(\frac{1}{y}\)

⇒ or, \(x y=\frac{k d-b}{a-k c}=k_1=\text { constant }\)

⇒ when \(k_1=\frac{k d-b}{a-k c}\)

Example 7. If x ∝ y and y ∝ z then show that x + y ∝ z.

Solution: x ∝ y ⇒ x = k₁y,

⇒ y ∝ z ⇒ y =k₂z [k_{1 ,}k₂ are non zero constant]

⇒ Now, \(\frac{x+y}{z}=\frac{k_1 k_2 z+k_2 z}{z}=\frac{\left(k_1 k_2+k_2\right)}{z} \cdot z\)

= (k k k) = constant

∴ x + y ∝ z..

Example 8. If P²– Q² ∝ PQ then show that (P + Q) ∝ (P- Q)

Solution: P² + Q² = 2KPQ [2k is a non-zero variation constant]

⇒  or, \(\frac{\mathrm{P}^2+\mathrm{Q}^2}{2 \mathrm{PQ}}=\mathrm{k}\)

⇒ or, \(\frac{\mathrm{P}^2+\mathrm{Q}^2+2 \mathrm{PQ}}{\mathrm{P}^2+\mathrm{Q}^2-2 \mathrm{PQ}}=\frac{k+1}{k-1}\) [by components dividends]

⇒ or, \(\frac{(\mathrm{P}+\mathrm{Q})^2}{(\mathrm{P}-\mathrm{Q})^2}=\frac{k+1}{k-1}\)

∴ \(\frac{\mathrm{P}+\mathrm{Q}}{\mathrm{P}-\mathrm{Q}}= \pm \sqrt{\frac{k+1}{k-1}}=\text { constant. }\)

⇒ p + Q ∝ P – Q

Example 9. x ∝ y when z constant and x ∝ \(\frac{1}{z}\) when y constant. If y = b when z = c, x = a then find the value of x when y = b², z = c².

Solution: x ∝ y (z constant.) x ∝ \(\frac{1}{z}\) (y constant.)

By compound variation, x ∝ \(\frac{y}{z}\) (y, z vary)

∴ x = k\(\frac{y}{z}\) [k is a non zero variation constant.]

⇒ Q = k\(\frac{b}{c}\)

⇒ k = k\(\frac{ac}{b}\)

Class 10 Maths Algebra Important Questions

Example 10. If \(x^3-\frac{1}{y^3} \propto x^3+\frac{1}{y^3}\) then show that x ∝ \(\frac{1}{y}\)

Solution: \(x^3-\frac{1}{y^3}=k\left(x^3+\frac{1}{y^3}\right)\)

⇒  or, \(\frac{x^3-\frac{1}{y^3}}{x^3+\frac{1}{y^3}}=k\)

⇒  or, \(\frac{2 x^3}{-2 \frac{1}{y^3}}=\frac{k+1}{k-1}\)

⇒ or, \(x^3 y^3=\frac{k+1}{1-k}\)

⇒ or, \(x y=\sqrt[3]{\frac{k+1}{1-k}}\) = constant

∴ \(\quad x \propto \frac{1}{y}\)

Trigonometry Chapter 1 Concept Of Measurement Of Angle

⇔ Positive angle: If the rotating ray rotates anticlockwise direction, the angle formed is called positive angle.

∠AOB is a positive angle.

⇔ Negative angle: If the rotating ray rotates clockwise direction, the angle formed is called negative angle.

∠AOB is a negative angle.

Read and Learn More WBBSE Solutions for Class 10 Maths

If a ray of an angle comes back to its first position after one complete rotation in anticlockwise direction, then the measurement of an angle is 360°, while in clockwise direction, the angle is then -360°.

∠AOB = + θ

∠AOC = 360° + θ

Class 10 Maths Trigonometry Chapter 1 Solutions

∠POQ = – θ

∠POR =- (360° + θ)

There are two general systems to measure trigonometrical angles are

1. Sexagesimal system and
2. Circular system.

⇔ Sexagesimal system: The angle formed by two perpendicular intersecting lines is called right angle.

1 right angle = 90°

1° = 60′

1′ = 60″

⇔ Circular system: The measure of an angle subtended at the centre by an arc having equal length with radius is called one radian and it is written as 1^c.

If \(\overline{\mathrm{OA}}=\widehat{A B}\) = r then ∠AOB = 1^c

π^c = 180°

Trigonometric Ratios Class 10 Solutions

Trigonometry Chapter 1 Concept Of Measurement Of Angle True Or False

Example 1. The angle, formed by rotating a ray centering its end point in an anticlockwise direction is positive.

Solution: The statements is true

Example 2. The angle, formed for completely rotating a ray twice by centering its end point is 720°

Solution: The statement is true.

Example 3. The circular value of (- 100°) is \(\frac{5 \pi^c}{9}\)

Solution: 180° = π^c

∴ The statement is True.

Example 4. The sexagesimal value of an angle formed by the end point of second hand of a clock in 1 minute rotation is 180°

Solution: In 1 minute the angle formed by the end point of second hand of a clock is 360°.

The statement is False.

Example 5. The circular value of each angle of an equilateral triangle is \(\frac{\pi^c}{3}\).

Solution: The sexagesimal value of each angle of an equilateral triangle is 60°.

180° = π^c

∴ \(60^{\circ}=\frac{60 \pi^c}{180}=\frac{\pi^c}{3}\)

The statement is True.

Class 10 Trigonometry Chapter 1 Solved Examples

Trigonometry Chapter 1 Concept Of Measurement Of Angle Fill In The Blanks

Example 1. π radian is a ______ angle.

Solution: Constant [Because radian = 180°]

Example 2. In sexagesimal system 1 radian equal to _______ (approx).

Solution: \(\frac{22}{7}\) radian = 180°

1 radian = \(\frac{7}{22}\) x 180° = \(\frac{7 \times 90^{\circ}}{11}=\frac{630^{\circ}}{1.1}\)

= 57°16’22” (approx)

∴ 57°16’22” (approx.)

Wbbse Class 10 Trigonometry Notes

Example 3. The circular value of the supplementary angle of the measure is \(\frac{3 \pi}{8}\) is _______

Solution: The circular value of the supplementary angle of the measure is \(\frac{3 \pi}{8}\) is \(\left(\pi-\frac{3 \pi}{8}\right)\) or \(\frac{5\pi}{8}\)

∴ Answer is \(\frac{5 \pi}{8}\)

Example 4. The circular value of an angle in a ________ is \(\frac{\pi^c}{2}\)

Solution: Semicircle.

Example 5. The circular value of a clock at 9 a.m. is ______

Solution: \(\frac{\pi^c}{2}\)

Trigonometry Chapter 1 Concept Of Measurement Of Angle Short Answer Type Questions

Example 1. If the value of an angle in degree is D and in radian is R; then determine the value of \(\frac{R}{D}\)

Solution: 180° = π^c

According to question R = \(\frac{D}{180}\)

⇒ \(\frac{R}{D}\) = \(\frac{\pi}{180}\)

Example 2. Write the value of the complementary angle of the measure 63°35’15”

Solution: The complementary angle of 63°35’15” is (90° – 63°35’15”) is 16°24’45”

90° = 89°59’60” – 63°35’15” = 16°24’45”

Trigonometric Ratios Formulas Class 10

Example 3. If the measures of two angles of a triangle are 65°56’55” and 64°3’5”, then determine the circular value of third angle.

Solution: The measures of third angle of a triangle is {180°- (65°56’55” + 64°3’5″)}

= 180° – 129°59’60” = 180° – 130° = 50°

180° = π^c or, \(50^{\circ}=\frac{50}{180} \pi^c=\frac{5 \pi^c}{18}\)

∴ The circular value of third angle \(\frac{5 \pi^c}{18}\)

Example 4. In a circle, if an arc of 220 cm length subtends an angle of measure 63° at the centre, then determine the radius of the circle.

Solution: Let the radius of the circle is r cm. Here arc (s) = 220 cm

Circular value of 63° = \(\left(\frac{63}{180} \times \frac{22}{7}\right)\) radian

= \(\frac{11}{10}\) radian

∴ θ = \(\frac{11}{10}\) radian

s = rθ

220 = r x \(\frac{11}{10}\)

⇒ r = \(\frac{220 \times 10}{11}\) = 200

∴ radius of the circle is 200 cm.

Example 5. Write the circular value of an angle formed by the end point of hour hand of a clock in 1 hour rotation.

Solution: Sexagesimal value of an angle formed by the end point of hour hand of a clock in 1 hour rotation is \(\frac{360^{\circ}}{12}\) or 30°

180° = π^c

30° = \(\frac{30}{180} \pi^c=\frac{\pi^c}{6}\)

∴ The circular value is \(\frac{\pi^c}{6}\)

Example 6. Find the circular value of 30°30’30”.

Solution: 30°30’30”

= 30° + 30′ + 30″

= 30° + 30′ + \(\left(\frac{30}{60}\right)^{\prime}\) [60″ = 1′]

= 30° + 30′ + \(\frac{1^{\prime}}{2}\) = 30° + \(\left(30+\frac{1}{2}\right)^{\prime}\)

= 30° + \(\left(\frac{61}{2 \times 60}\right)^{\circ}\) [60″ = 1′]

= \(\left(30+\frac{61}{120}\right)^{\circ}=\left(\frac{3661}{120}\right)^{\circ}\)

∴ \(\frac{3661^{\circ}}{120}=\frac{3661}{120 \times 180} \pi^c=\frac{3661}{21600} \pi^c\)

Class 10 Maths Trigonometry Important Questions

Example 7. If the measures of two angles of a triangle are 70°38’24” and 34°21’36” then determine the sexagesimal value and the circular, value of the third angle.

Solution: Sum of two angles is (70°38’24” + 34°21’36”)

= 104°59’60” = 104°60′ = 105°

The value of the third angle = 180° – 105° = 75°

180° = π^c

∴ The sexagesimal value is 75° and circular value is \(\frac{5 \pi^c}{12}\)

Example 8. Determine the length of an arc of a circle with radius 12 cm in lengths which makes an angle at the centre is 120°.

Solution: In a circle of radius r unit in length, if the circular value of an angle subtended by an arc of S unit in length at the center is θ, then S = rθ

given, r = 12 cm

and \(\theta=\frac{120}{180} \pi^c=\frac{2 \pi^c}{3}\)

∴ S = \(12 \times \frac{2 \pi}{3} \mathrm{~cm}\)

= \(8 \times \frac{22}{7} \mathrm{~cm}=\frac{176}{7} \mathrm{~cm}=25 \cdot 14 \mathrm{~cm} \text { (approx) }\)

∴ Length of the arc is 25.14 cm (approx)

Arithmetic Chapter 1 Revision

Question 1. Convert the following to a fraction:

1. 7.028
Solution:

Let x = 7.02828…

1000x= 7028.28…

Multiply ‘x’ by 10 to align the repeating parts 10x = 70.2828…..

Subtract the second equation from the first to eliminate 1000x – 10x = 7028.2828……..70.2828…

990x = 6958

Finding the greatest common divisor (GCD) of 6958 and 990

The GCD of 6958 and 990 is ‘2’ \(\frac{6958 \div 2}{990 \div 2}=\frac{3479}{495}\)

So the recurring decimal 7.02828 as a fraction is \(\frac{3479}{495}\)

∴ \(7.0 \dot{2}=17 \frac{14}{495}\)

2. 3.432
Solution:

Let x = 3.43232··…

Multiply x by 1000

1000x = 3432.32…..

Multiply x by 10 to align the repeating parts.

10x = 34.32.32……

Subtract the second equation from the First to eliminate the repeating part

4000x – 10x = 3432.323232……..34.3232…

990x = 3398

x = \(\frac{3398}{990}\)

Finding the Greatest common divisor (GCD) of 3398 and 990.

The GCD of 3398 and 990 are 2

∴ \(\frac{3398 \div 2}{990 \div 2}=\frac{1649}{495}\)

So the recurring decimal \(3 \cdot 4 \overline{32}\) as a fraction is \(\frac{1699}{495}\)

∴ \(3.4 \dot{3} \dot{2}=3 \frac{214}{495}\)

Class 7 Arithmetic Problems With Solutions

Question 2. Convert the following percentage into decimal fractions:

1. 0.03
2. 1.26

Solution:

1. 0.03

Decimal Fraction = \(\frac{0.03}{100}\) = 0.0003

0.03% = 0.0003

2. 1·26

Decimal Fraction = \(\frac{1.26}{100}\)

= 0.0126

1.26% = 0.0126

Question 3. Express the Following in percentage:

1. ₹5 out of ₹25
2. 0.3

Solution:

percentage = \(\left(\frac{\text { Part }}{\text { Whole }}\right) \times 100\)

Here part is 5 and the whole is 25

percentage = (\(\frac{5}{25}\))x100

= (0.2) x 100

percentage = 20%

∴ ₹5 out of ₹25 is 20%.

2. 0.3

To Convert the decimal 0.3 to a percentage, we multiply by 100.

percentage = 0.3× 100 = 30%

Question 4. Find the values of the following.

1. 18% of 3600
2. 12 \(\frac{1}{2}\) % of ₹12.08

Solution:

1. 18% of 3600

⇒ 3600 x \(\frac{18}{100}\)

⇒ 36 x 18

⇒ 648

∴ 18% of 3600 = 648

2. 12\(\frac{1}{2}\) % of 12.08.

⇒ 12.08 x \(\frac{25}{2 \times 100}\)

⇒ 12.08 x \(\frac{1}{8}\)

⇒ 12.08 × 0.125

⇒ 1.51

∴ 12 \(\frac{1}{2}\)% of ₹12.08 is ₹1.51

Class 7 Maths Chapter 1 Solved Exercises

Question 5. If the product of two numbers is 150 and their quotient is \(\frac{3}{2}\) then find the numbers.
Solution:

Let’s denote the two numbers as x and y.

Given

1. The product of two numbers is 150:xy = 150
2. The quotient of the two numbers is \(\frac{3}{2}\):\(\frac{x}{y}\)= \(\frac{3}{2}\)

From the second condition. \(\frac{x}{y}\) = \(\frac{3}{2}\)

x = \(\frac{3}{2}\) y

Now Substitute the ‘x’ value in 1-condition.

xy= 150

(\(\frac{3}{2}\)y)y = 150

⇒ \(\frac{3}{2}\)y² = 150

y² = 150 x \(\frac{2}{3}\)

y² = 100

y = √100

y = 10

Now that we have found y = 10, we can find x.

x = \(\frac{3}{2}\) x 10

x = 15

So the two numbers are x = 15 and y = 10.

Question 6. If the sum of two numbers is so and their HCF is 16 then Find the numbers.
Solution:

Let’s denote the two numbers as x and y.

Given

1. The sum of the two numbers is 80: x+y=80.
2. Their highest Common Factor (HCF) is 16.

Let’s express x and y as

x = 16a

y = 16b

where a and b are integers.

Now we substitute these expressions into the equation for their sum:

16a + 16b = 80

16(a+b)=80

(a+b) = \(\frac{80}{16}\)

a+b = 5

since a+b=5, and a and b are integers the

Possible values for a and b are a = 1, and b=4 (or) a=2, and b=3.

So the numbers are 16×1 = 16, and 16×4 = 64,08 16×2=32, and 16×3=48.

∴ The two numbers are 16 and 64 (or) 32 and 48.

Arithmetic Formulas For Class 7 WBBSE

Question 7. Find the square roots of the following numbers:

1. 11025
Solution:

To Find the square root use prime factorization.

First, let’s see if it’s a perfect square by trying

Some divisors.

11025 ÷ 25 = 441

So, we have;

11025 = 25X441

441 = 21×21

25 = 5×5

Thus

11025 = 5² x 21²

Take the square root: \(\sqrt{11025}=\sqrt{(5 \times 21)^2}\)

= \(5 \times 21\)

∴ \(\sqrt{11025}\) = 105

Question 8. Find the square root of the following numbers.

1. 15376
Solution:

First, let’s see if it’s a perfect square by trying Some divisors.

15376 ÷ 16 = 961.

15376 = 16×961

961 = 31×31

16 = 4×4.

Thus 15376 = 4² x 31²

So we can take the square root: \(\sqrt{15376}=\sqrt{(4 \times 31)^2}\)

= \(4 \times 31\)

∴ \(\sqrt{15376}\) = 124

Question 9. Parthababu pays 157. of his salary for house rent. If he pays 4500 per month for rent, then find his monthly salary.
Solution:

Let’s denote Partha babu’s monthly salary as ‘s’.

Given,

House rent = 15% of salary.

House rent = 4500.

15% of S = 4500

⇒ \(\frac{15}{100}\) X S = 4500

S = \(\frac{4500}{0.15}\)

S = 30000

∴ so Parthababu’s monthly salary is 30000.

WBBSE Maths Study Material Class 7

Question 10. A General wishing to arrange his soldiers 632 in number into a solid square found that there were 7 Soldiers over. How many were there in the front?
Solution:

Let’s denote the number of soldiers on each side of the Square as 2.

The total number of soldiers is 632 and there are 7 extra soldiers.

x² +7=632 2

x = 632-7

x² = 625

x = √625

x = 25

So there are 25 soldiers on each side of the square.

∴ 25 Soldiers on each FRONT SIDE

Question 11. 15 men working 6 hours a day can do a piece of work in 20 days. How many men working 8 hours a day Can do it in 25 days?
Solution:

Given:

15 men work 6 hours a day to complete the work in 20 days.

Total man-hours = Number of men x Number of hours per day X Number of days.

Total man-hours = 15×6×20

Now, The total man-hours For the second scenario

The number of days is 25

The number of hours per day is ‘8’

we need to find out how many men are required.

Let’s denote the number of men required as ‘x’

15×6×20 = x x 8 x 25

1800 = 200x

x = \(\frac{1800}{200}\)

x = 9

So, 9 men are required to complete the work in 25 days working 8 hours a day.

Question 12. Simplify \(\frac{2.8 \text { of } 2.2 \ddot{2}}{1.3 \dot{3}}+\left\{\frac{4.4-2.83}{1.3+2.629}\right\}\)of 8.2
Solution:

⇒ \(\frac{2.8 \times 2.27}{1.36}+\left\{\frac{4.4-2.83}{1.3+2.629}\right\} \times 8.2\)

⇒ \(\frac{6.356}{1.36}+\left\{\frac{1.57}{3.929}\right\} \times 8.2\)

⇒ \(4.67352+\{0.39959\} \times 8.2\)

⇒ 4.67352+3.276638

⇒ \(7.950158 \simeq 8\)

∴ \(\frac{2.80 f 2.27}{1.36}+\left\{\frac{4.4-2.83}{1.3+2.629}\right\}\) of 8.2 is = 8

Class 7 Maths Arithmetic Solutions WBBSE

Question 13. Write the ratio of the three angles of an isosceles Yright-angled triangle.
Solution:

Given the total sum of angles in any triangle is 180°

Let’s denote the two equal angles as ‘X’

The equation for the sum of angles in the triangle is

90+X+X = 180°

2x+90° = 180°

2x = 180-90°

2x = 90°

x = 90°/2

X = 45°

∴ The three angles in the triangle are 90°, 45° and 45°

The ratios of these angles are 90:45:45

Dividing each term by 45 is 2:1:1

∴ The ratio of the three angles in a right-angled

Isosceles triangle is 1:2:1

Question 14. The ratio of textbooks and story books in a School library is 3:5. If a number of textbooks is 864, then find the number of story books.
Solution:

Given:

The ratio of textbooks to storybooks= 3:5

If the number of textbooks is 864

we can set up a proportion to find the number of Storybooks:

Let x’ be the number of storybooks \(\frac{\text { Number of textbooks }}{\text { Number of story books }}=\frac{3}{5}\)

⇒ \(\frac{864}{x}=\frac{3}{5}\)

864 x 5 = 3x

4320 = 3x

x = \(\frac{4320}{3}\)

x = 1440

∴ So the number of story books is x = 1440.

Question 15. verify which of the following numbers are in proportion:

1. 4,6,7,8
Solution:

Given numbers are 4, 6, 7, 8

Let’s check the ratios:

1. Ratio of 4 to 6:\(\frac{4}{6}\) = \(\frac{2}{3}\)

2. Ratio of 6 to 7:\(\frac{6}{7}\)

3. Ratio of 7 t0 8: \(\frac{7}{8}\)

“If the ratios of consecutive pairs are equal, then the numbers are in proportion”

∴ \(\frac{6}{7}\) = 0.8571

∴ \(\frac{7}{8}\) = 0.875

The ratio of 6 to 7 is approximately 0.8571 and the ratio of 7 to 8 is 0.875. These two ratios are not equal.

The ratios of consecutive pairs are not equal, the numbers 4, 6, 7, and 8 are not in proportion.

Class 7 Maths Arithmetic Solutions WBBSE

Question 16. Verify which of the following numbers are in Proportion.

1. 8,12,6,9
Solution:

The given numbers are 8, 12, 6 and 9.

Let’s check the ratios:

1. Ratio of 8 to 12:\(\frac{8}{12}\) = \(\frac{2}{3}\)

2. Ratio of 12 to 6:\(\frac{12}{6}\) = 2

3. Ratio of 6 to 9:\(\frac{6}{9}\) = \(\frac{2}{3}\)

“If the ratios of consecutive pairs are equal, then the numbers are in proportion?”

1. \(\frac{8}{12}\) = \(\frac{2}{3}\)
2. \(\frac{12}{6}\) = 2
3. \(\frac{6}{9}\) = \(\frac{2}{3}\)

The ratios of Consecutive pairs are equal \(\frac{2}{3}\) the numbers 8, 12, 6, and 9 are in proportion.

Question 17. Verify which of the following numbers core in proportion.

1. \(\frac{1}{2}, \frac{1}{6}, \frac{1}{3}\) and \(\frac{1}{9}\)
Solution:

The given numbers are \(\frac{1}{2}, \frac{1}{6}, \frac{1}{3}\) and \(\frac{1}{9}\)

Let’s check the ratios:

1. Ratio of \(\frac{1}{2}\) to \(\frac{1}{6}\):

⇒ \(\frac{\frac{1}{2}}{\frac{1}{6}}=\frac{1}{2} \times \frac{6}{1}=3 \text {. }\)

2. Ratio of \(\frac{1}{6}\) to \(\frac{1}{3}\):

⇒ \(\frac{\frac{1}{6}}{\frac{1}{3}}=\frac{1}{6} \times \frac{3}{1}=\frac{1}{2}\)

3. Ratio of \(\frac{1}{3}\) to \(\frac{1}{9}\):

⇒ \(\frac{\frac{1}{3}}{\frac{1}{9}}=\frac{1}{3} \times \frac{9}{1}=3\)

“If the ratios of consecutive pairs are equal, then the numbers are in proportion”

∴ All the ratios are equal to 3 the numbers \(\frac{1}{2}, \frac{1}{6}, \frac{1}{3}\) and \(\frac{1}{9}\) are in proportion.

2. Simplify: \(\frac{3}{5} \div 4 \frac{1}{3} \times 7 \frac{1}{5}+999 \frac{324}{325} \times 324\)
Solution:

⇒ \(\frac{3}{5} \div 4 \frac{1}{3} \times 7 \frac{1}{5}+999 \frac{324}{325} \times 324\)

⇒ \(\frac{3}{5} \div \frac{13}{3} \times \frac{36}{5}+\frac{324999}{325} \times 324\)

⇒ 0·6÷4·3 × 7·2+ 999.9969 x 324

⇒ 0·139534 × 7·2 + 323999.0030

⇒ 1.0046 + 323999.0030

⇒ 324000.0076.

∴ \(\frac{3}{5} \div 4 \frac{1}{3} \times 7 \frac{1}{5}+999 \frac{324}{325} \times 324=324000\)

Arithmetic Formulas For Class 7 WBBSE

Question 18. Find the greatest number that divides 175,220, and 325 to keep equal remainder in all cases.
Solution:

To find the greatest number that divides, 175, 220, and 325 while keeping equal remainders in all cases

we need to find the greatest common divisor (GCD) of the differences between these numbers.

Let ‘d’ be the Common difference then we have:

175-d = 220-d = 325-d.

Subtracting each pair of numbers we get,

220-175 = 45

325-220 = 105

325 175 = 150

Now, we need to find the greatest common divisor of these differences: 45, 105, and 150.

GCD(45,105,150) = 15

∴ The greatest number that divides 175,220, and 325 to keep equal remainder in all cases is 15.