Haritha

Arithmetic Chapter 3 Rational Number

Natural Numbers: 1, 2, 3, 4, 5……., 125, ……. are counting numbers or natural numbers such that 1 is the first natural number and there is no last natural number.

⇒ The natural number is denoted by N and is written as N = (1, 2, 3, 4, . . . . . . . ., 125,…..)

Whole Numbers: The numbers 0, 1, 2, 3,….., and 125, are called whole numbers.

Read and Learn More WBBSE Solutions For Class 8 Maths

⇒ The whole number is denoted by W and is written as W = (0, 1, 2, 3,…… 125, …)

Integers: The numbers …. -4, -3, -2, -1; 0, 1, 2, 3 ….. are called Integers.

⇒ The Integers is denoted by Z and is written as Z = (..,-3, -2, -1, 0, 1, 2, 3…..)

⇒ The integers greater than 0, i.e. 1, 2, 3 ….. are called positive Integers and the Integers less than 0, i,.e. -1, -2, -3,…. are called negative Integers.

⇒ 0 (zero) is an Integer that is neither positive nor negative.

Differece Between Rational And Irrational Numbers 

Rational Numbers: The numbers which can be expressed in the form of \(\frac{p}{q}\) where p and q are integers and q ≠ 0 are called Rational Numbers.

Example: 6, \(\frac{3}{9}\), 0, \(\frac{5}{6}\) etc. [All integers are Rational Numbers]

Irrational Numbers: The numbers which cannot be expressed in the form of \(\frac{p}{q}\) where p and q are integers and q ≠ 0 are called Irrational Numbers.

Example: √3, π etc.

Real Number:

1. Rational Number
2. Irrational Number

Some important points:

1. If two rational numbers x and y such that x < y there is a rational number. \(\frac{x+y}{2}\) i.e. x < \(\frac{x+y}{2}\) < y

2. If x and y are two rational numbers and x < y then n rational numbers between x and y are (x + d), (x + 2d), (x + 3d),…….. (x + nd), where d = \(\frac{y-x}{n+1}\)

3. If the rational numbers of the far \(\frac{p}{q}\) be expressed into decimals, it will be terminating into decimals it will be terminating decimal number, where q has prime factors 2 and 5 only.

4. If the rational numbers of the form be expressed into recurring decimals where has prime factors other than 2 and 5.

5. If rational numbers are expanded into decimals it will be terminating or recurring and the fraction whose decimal form is terminating or recurring will be rational.

6.

1. Sum of rational numbers are rational.
2. Difference of rational numbers are rational.
3. Product of rational numbers are rational.
4. Quotient of two rational numbers (not divided by 0) are rational.

7. If a, b, c are rational numbers.

Associative Law:

⇒ a + (b + c) = (a + b) + c [Associative law of addition]

⇒ But a (b – c) (a – b) – c [Associative law does not exists for subtraction]

⇒ and a x (b x c) = (a x b) x c [Associative law for product]

Commutative law:

⇒ a + b = b + a (for addition)

⇒ a – b + b – a (not exist for subtraction)

⇒ a x b = b x a (for product)

⇒ \(\frac{a}{b}\) \(\frac{b}{a}\) (not exist for division)

Distributive law:

⇒ a x (b+c) = a x b + a x c

Arithmetic Chapter 3 Rational Number Examples

Example 1. Find the value of (2x + 5) when x = –\(\frac{3}{8}\)

Solution:

Given f(x) = 2x + 5 and x = –\(\frac{3}{8}\)

⇒  f(-\(\frac{3}{8}\)) = 2 × (-\(\frac{3}{8}\))+5

⇒  f(-\(\frac{3}{8}\)) = – (2 × (\(\frac{3}{8}\)) +5

⇒  f(-\(\frac{3}{8}\)) = \(\frac{3}{4}+5\)

⇒  f(-\(\frac{3}{8}\)) = \(\frac{-3+20}{4}\)

⇒  f(-\(\frac{3}{8}\)) = \(\frac{17}{4}\)

⇒  f(-\(\frac{3}{8}\)) = 4 \(\frac{1}{4}\)

∴ The Value of f(x) = 2x + 5 = 4 \(\frac{1}{4}\)

Example 2. Solve the following equations and express the roots in form (where q ≠ 0 and p, q are two integers)

1. 3x – 7 = 0
2. y = 15 + 10y

Solution:

Given That :

f(x) = 3x – 7 = 0

⇒ 3x = 7

⇒ x = \(\frac{7}{3}\)

∴ x = \(\frac{7}{3}\)

∴ The root of the equations is ( X – \(\frac{7}{3}\)) =0

f(y) ⇒ y = 15 + 10y

y = 15 + 10y

⇒ y – 10y = 15

⇒ – 9y = 15

⇒ y = –\(\frac{15}{9}\)

⇒ y = \(\frac{-5}{3}\)

∴ y = \(\frac{-5}{3}\)

∴ The root of the equations is ( y + \(\frac{5}{3}\) ) = 0

Example 3. Write the approximate number in the following boxes:

1. x \(\frac{-5}{3}\) = 1
2. (-\(\frac{6}{11}\)) + (\(\frac{7}{12}\)) = 

Solution :

1. x –\(\frac{5}{3}\) = 1 ⇒  = -1 x \(\frac{13}{5}\) = –\(\frac{13}{5}\)
2. (-\(\frac{6}{11}\)) + (\(\frac{7}{12}\)) = \(\frac{-72+77}{132}=\frac{5}{132}\)

Example 4. Write the product by multiplying \(\frac{4}{25}\) with the reciprocal of (-\(\frac{2}{15}\)).

Solution: The reciprocal of (-\(\frac{2}{15}\)) is (-\(\frac{15}{2}\))

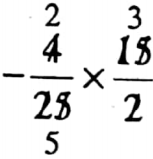
= \(-\frac{6}{5}\)

Example 5. Find the value of the following with the help of Commutative law and Associative law.

1. \(\frac{7}{9} \times\left(-\frac{11}{25}\right) \times\left(-\frac{87}{42}\right) \times\left(\frac{5}{121}\right)\)
2. \(\frac{3}{4}+\left(-\frac{7}{10}\right)+\frac{5}{6}+\left(-\frac{12}{25}\right)\)

Solution:

1. \(\frac{7}{9} \times\left(-\frac{11}{25}\right) \times\left(-\frac{87}{42}\right) \times \frac{5}{121}\)

= \(\frac{7}{9} \times\left\{\left(-\frac{11}{25}\right) \times\left(-\frac{87}{42}\right)\right\} \times \frac{5}{121}\)

= \(\frac{7}{9} \times\left\{\left(-\frac{87}{42}\right) \times\left(-\frac{11}{25}\right)\right\} \times \frac{5}{121}\)

[I get with the help of Commutative Law and Associative Law]

2. \(\frac{3}{4}+\left(-\frac{7}{10}\right)+\frac{5}{6}+\left(-\frac{12}{25}\right)\)

= \(\frac{3}{4}+\left\{\left(-\frac{7}{10}\right)+\frac{5}{6}\right\}+\left(-\frac{12}{25}\right)=\frac{3}{4}+\left\{\frac{5}{6}+\left(-\frac{7}{10}\right)\right\}+\left(-\frac{12}{25}\right)\)

= \(\left(\frac{3}{4}+\frac{5}{6}\right)+\left\{\left(-\frac{7}{10}\right)+\left(-\frac{12}{25}\right)\right\}=\left(\frac{9+10}{12}\right)+\left\{-\left(\frac{35+24}{50}\right)\right\}\)

= \(\left(\frac{19}{12}\right)+\left(-\frac{59}{50}\right)\) [I get with the help of Commutative Law and Associative Law]

= \(\frac{475-354}{300}=\frac{121}{300}\)

Example 6. Write three rational numbers between (-5) and (-4).

Solution: 3 rational numbers are -4.1 or, –\(\frac{41}{10}\), -4.3 or, –\(\frac{43}{10}\), -4.5 or –\(\frac{45}{10}\) as –\(\frac{9}{2}\)

Example 7. Write 10 rational numbers between –\(\frac{3}{5}\) and \(\frac{1}{2}\)

Solution: –\(\frac{3}{5}\) = –\(\frac{6}{10}\) = –\(\frac{12}{20}\), \(\frac{1}{2}\) = \(\frac{5}{10}\) = –\(\frac{10}{20}\)

∴ 10 rational numbers are: –\(\frac{9}{20}\), –\(\frac{7}{20}\), –\(\frac{5}{20}\), –\(\frac{3}{20}\), –\(\frac{1}{20}\), \(\frac{1}{20}\), \(\frac{3}{20}\), \(\frac{5}{20}\), \(\frac{7}{20}\), \(\frac{9}{20}\)

Example 8. Plot the number \(\frac{1}{4}\) on number line.

Solution:

Example 9. Plot -2\(\frac{3}{5}\) on number line.

Solution :

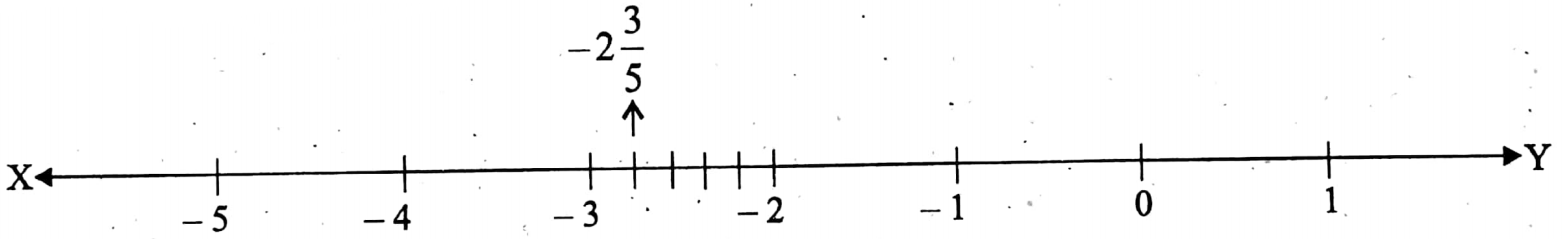
Example 10. Write 5 rational number lying between \(\frac{3}{5}\) and \(\frac{4}{5}\).

Solution: Here x = \(\frac{3}{5}\), y = \(\frac{4}{5}\), x = 5

d = \(d=\frac{y-x}{x+1}=\frac{\frac{4}{5}-\frac{3}{5}}{5+1}=\frac{\frac{1}{5}}{6}=\frac{1}{30}\)

∴ 5 rational numbers are: \(\left(\frac{3}{5}+\frac{1}{30}\right),\left(\frac{3}{5}+\frac{2}{30}\right),\left(\frac{3}{5}+\frac{3}{30}\right),\left(\frac{3}{5}+\frac{4}{30}\right),\left(\frac{3}{5}+\frac{5}{30}\right)\)

i.e. \(\frac{19}{30}, \frac{20}{30}, \frac{21}{30}, \frac{22}{30}, \frac{23}{30}\)

Example 11. Write 6 rational numbers lying between 5 and 6.

Solution: Write the equivalent rational numbers of 5 and 6 which have (6 + 1) or 7 as denominator.

5 = \(\frac{35}{7}\), 6 = \(\frac{42}{7}\)

∴ 6 rational numbers are: \(\frac{36}{7}, \frac{37}{7}, \frac{38}{7}, \frac{39}{7}, \frac{40}{7}, \frac{41}{7}\)

Example 12. Choose the correct answer

1. √2 is a

1. Rational number
2. Irrational number
3. Natural number
4. Whole number

Solution: √2 = 1.414…..

∴ So √2 is irrational number.

∴ So the correct answer is 2. Irrational number

√2 is a Irrational number.

2. Product of \(\frac{7}{18}\) and reciprocal of (-\(\frac{5}{6}\)) is

1. –\(\frac{7}{15}\)
2. –\(\frac{15}{7}\)
3. \(\frac{7}{15}\)
4. \(\frac{7}{15}\)

Solution: The reciprocal of (-\(\frac{5}{6}\)) is (-\(\frac{6}{5}\))

∴ So the correct answer is 1. –\(\frac{7}{15}\)

Product of \(\frac{7}{18}\) and reciprocal of (-\(\frac{5}{6}\)) is –\(\frac{7}{15}\)

3. a x \(\frac{1}{a}\) =? [where a is rational number and a ≠ 0]

1. 1
2. a
3. \(\frac{1}{a}\)
4. None of these

Solution: a x \(\frac{1}{a}\)

∴ So correct answer is 1. a x \(\frac{1}{a}\)

a x \(\frac{1}{a}\) =1.

Example 13. Write ‘True’ or ‘False’:

1. Commutative law of subtraction does not exist for rational numbers.

Answer: True.

2. \(-\frac{21}{29} p-\left(\frac{21}{29}\right)=0\)

Answer: False

3. If x = –\(\frac{2}{5}\) then, \(\frac{1}{x}\) + \(\frac{x}{2}\) = –\(\frac{10}{27}\)

Solution: \(\frac{1}{x}+\frac{x}{2}=\frac{1}{-\frac{2}{5}}+\frac{-\frac{2}{5}}{2}\)

= \(-\frac{5}{2}-\frac{2}{5} \times \frac{1}{2}=-\left(\frac{5}{2}+\frac{1}{5}\right)=-\left(\frac{25+2}{10}\right)=-\frac{27}{10}\)

∴ So, the statement is false.

Example 14. Fill in the blanks

1. √47 is a ______ number.

Answer: Irrational number

√47 is a Irrational number

2. \(\frac{2}{9}\) + ____ = 0

Answer: –\(\frac{2}{9}\)

\(\frac{2}{9}\) + \(\frac{2}{9}\)= 0

3. (-\(\frac{2}{3}\)) + 0 = _____

Answer: Undefined

(-\(\frac{2}{3}\)) + 0 = Undefined

Arithmetic Chapter 2 Pie Chart

A pie chart is a circular statistical graphic which is divided into slices to illustrate numerical proportions.

In a pie chart, the arc length of each slice is proportional to the quantity it represents.

In pie chart values of various datas of components are represented by sectors of a circle. The angle at the centre of the sector gives the value of the data.

Read and Learn More WBBSE Solutions For Class 8 Maths

At the centre, a circle makes a complete angle i.e. 360°.

Centre angle for a data = \(\left(\frac{\text { Value of the data }}{\text { Total value }} \times 360\right)^{\circ}\)

Method of drawing of Pie Chart:

1. Compute the central angles for the given datas using the above formula.
2. Draw a circle with any radius.
3. Divide the interior of the circle into different sectors having the angles as obtained (1) with the help of protractor.
4. Lable the sections properly to obtain the required pie chart.

Arithmetic Chapter 2 Pie Chart Examples

Example 1. There are 100 students in your class. The following table shows their hobby.

Draw a Pie Chart for the given data.

Solution:

Process:

Draw a circle with any radius (OA).

The central angle of the sector which represents the travel is 36°. So I draw ∠AOB 36° with the help of a protractor.

Now, I draw the sectors by reversing the protractor, the central angles of which are 18°, 216° and 90° respectively.

Thus I made a pie chart of the data.

Example 2. Arpita have made a model. She made a chart of expenditures of buying materials.

Make a pie chart with this information and write the central angle of the sectors.

Solution:

Example 3. The pie chart of what kind of programmes Information News the audience likes:

1. Write How many parts of the total circular region is the sector of the audience who watch news in the pie chart?
2. Write what kind of programme gets the most audience.
3. Write what kind of programme gets the least audience.
4. Write how many parts of the total audience watch the programmes of sports?

Solution:

1. No. of parts of total circular region is the sector of the audience who watch news in the pie chart is \(\frac{20}{360}\) or \(\frac{1}{18}\)
2. Entertaining programmes gets the most audience. [Entertained is 240°]
3. Informative programme gets the least audience.
4. \(\frac{90}{360}\) or \(\frac{1}{4}\) parts of the total audience watch the programmes of sports.

Example 4. Choose the correct Answer:

1. Pie Chart is also known as

1. Circle graph
2. Histogram
3. Bar graph
4. None of these

Answer: 1. Circle graph

2. Central angle for data

1. \(\frac{\text { Total value }}{\text { Value of the data }} \times 360^{\circ}\)
2. \(\frac{\text { Value of the data }}{\text { Total value }} \times 360^{\circ}\)
3. \(\frac{\text { Value of the data }}{\text { Total value }} \times 100^{\circ}\)
4. None of these

Answer: 2. \(\frac{\text { Value of the data }}{\text { Total value }} \times 360^{\circ}\)

3. A survey was made to find of music lovers like. If 20 people like classical music the number of people surveyed is

1. 100
2. 200
3. 50
4. 10

Answer: 2. 200

Example 5. Fill in the blanks:

1. Pie chart is also known as _______ graph.

Answer: Circle chart.

2. Study the following table below:

Measurement of central angle of Santro is ________

Solution: Measurement of central angle of santro is \(\left(\frac{6}{36} \times 360^{\circ}\right)=60^{\circ}\)

Answer: 60°

Example 6. Write ‘True’ or ‘False’.

1. Pie chart is a bar graph.

Answer: False

2. The whole circle represents the sum of the value of the components.

Answer: True

Arithmetic Chapter 1 Ratios And Proportion Examples

Example 1. If a: b = 2:3 and b: c = 4: 5, then find the value a: b: c.

Solution:

Given That : 

a : b = 2 : 3

b: c = 4: 5

a: b: c = ?

⇒ a : b = 2 : 3

Now Multiply the  a : b  with 4 we get,

⇒ (2 x 4) : (3 x 4)

∴ a : b = 8 : 12

⇒ b : c = 4 : 5

Now Multiply the  b : c with 3 we get,

⇒ b : c = (4 x 3) : (5 x 3)

⇒ b : c = 12 : 15

∴ a : b : c = 8 : 12 : 15

The value a: b: c is  8 : 12 : 15

Example 2. Find the compound ratio of x²: yz, y²: zx, and z²: xy.

Solution: The compound ratio of x² = yz, y² = zx and z²: xy

From The Above Given Equation

We Consider That L . H .S = R . H . S

= x² x y² x z² : yz x zx x xy

= x²y²z² : x²y²z²

= 1:1

∴ The compound ratio of x² = yz, y² = zx and z²: xy is 1:1

Read and Learn More WBBSE Solutions For Class 8 Maths

Example 3. Find the mean proportional of a² and b²c².

Solution: The mean proportional of a² and b²c² =

± \(\sqrt{a^2 \times b^2 c^2}\)

= ± abc.

The mean proportional of a² and b²c² = ± abc.

Example 4. If (3+\(\frac{4}{x}\)) : (5+\(\frac{2}{x}\)) = 1, then find the value of x.

Solution:

Given That : (3+\(\frac{4}{x}\)) : (5+\(\frac{2}{x}\)) = 1

⇒ (3+\(\frac{4}{x}\)) : (5+\(\frac{2}{x}\)) = 1

⇒ \(\frac{3+\frac{4}{x}}{5+\frac{2}{x}}=1\)

⇒ \(3+\frac{4}{x}=5+\frac{2}{x}\)

By taking the all ‘X‘ terms in on one side and Numericals to Other Side. We get,

⇒ \(\frac{4}{x}-\frac{2}{x}=5-3\)

⇒ \(\frac{2}{x}=2\)

⇒ 2x = 2

⇒ \(x=\frac{2}{2}=1\)

∴ The Value of the ‘ X ‘ is : 1

Example 5. What is the value of \(\sqrt{6 \cdot 76}-\sqrt{5 \cdot 76}+\sqrt{42 \cdot 25}\).

Solution:

Given That: \(\sqrt{6 \cdot 76}-\sqrt{5 \cdot 76}+\sqrt{42 \cdot 25}\)

⇒ \(\sqrt{6 \cdot 76}-\sqrt{5 \cdot 76}+\sqrt{42 \cdot 25}\)

By Taking the Determination to the Equation We Get,

= 2.6 – 2.4 + 6.5 = 0.2 + 6.5 = 6:7.

The value of \(\sqrt{6 \cdot 76}-\sqrt{5 \cdot 76}+\sqrt{42 \cdot 25}\) is 6:7

Example 6. Find the approximate value of 7 hour 12 min 40 sec. in minutes.

Solution:

First We convert sec into minutes

40 sec = \(\frac{40}{60}\) min

= \(\frac{2}{3}\) min.

= 0.66 min.

40 sec = 1 min. (approximate)

∴ 7 hour 12 min 40 sec = 7 hour + (12 + 1) min.

⇒ 7 hour 13 min.

∴ 7 hour 12 min 40 sec = 7 hour 13 min.

Example 7. Find the square root of 3\(\frac{814}{1225}\).

Solution: \(\sqrt{3 \frac{814}{1225}}=\sqrt{\frac{4489}{1225}}=\frac{67}{35}=1 \frac{32}{35}\)

Example 8. If the length of a square becomes double, then what will be changed its areas?

Solution:

we know that all sides in a square are equal.

⇒ Let the length of each side of a square be x units.

Area is x² sq.m.

If length of each side becomes double, then area is (2x)² or 4x² sq.unit.

∴ The area will be \(\frac{4 x^2}{x^2}\) or 4 times of original areas.

Example 9. If 8 men can do a piece of work in 15 days, then how many days can 12 men do that works?

Solution: Let 12 men can do the work in x days. [x > 0]

In the mathematical language the problem is:

Men
8
12

Time taken (day)
15
x

It is the case of inverse proportion.

So the proportion is

12: 8 : : 15: x

⇒ x = \(\frac{8 \times 15}{12}\)

⇒ x = 10

∴ 12 men can do a piece of work in 10 days,

Example 10. A train 200 meter long passes a tree in 12 sec. Find the speed of the train.

Solution: In passing the tree, the train must travel its own length i.e. 200 m.

The problem in mathematical language is:

Time taken (sec)
12
3600

Distance covered (meter)
200
?

According to the properties of ratio proportion we get,

12 : 3600 : : 200 : Distance covered in 1 hour.

∴ Distance covered in 1 hour = \(\frac{3600 \times 200}{12}\) meter 60000 meter = 60 km.

∴ Speed of the train is 60 km/hr.

Example 11. A train running at \(\frac{4}{7}\) of its own speed reached a place in 14 hours. In what time could it reach these running at its own speed?

Solution: Let speed of the train is x km/hr.

If the speed of the train is (x x \(\frac{4}{7}\)) km/hr or \(\frac{4x}{7}\) km/hr, then the train travels at a distance in 14 hours is (14 x \(\frac{4 x}{7}\)) km or 8x km.

The required time to cover a distance of 8x km with speed x km/hr is \(\frac{8x}{x}\) hour or 8 hours.

∴ The required time is 8 hours.

In 8 hours time could it reach these running at its own speed

Example 12. There is a path of 3 m width all around outside the square shaped park. The perimeter of the park including the path is 484 m. Calculate the area of the path.

Solution: The perimeter of the square park including the path is 484 m.

∴ The length of each side of the park including the path is \(\frac{484}{4}\) m or 121 m.

As the path is 3m width.

So length of each side of the park is (121 – 2 x 3) m or 115 m.

Area of the square park is (115)² sq.m. = 13225 sq.m.

Area of the park including the path is (121)² sq.m. = 14641 sq.m.

∴ The area of the path = (14641 – 13225). sq.m. = 1416 sq.m

Example 13. Choose the correct answer.

1. The compound ratio of 2: 3, 4: 5, and 7: 8 is

1. 15: 7
2. 7: 15
3. 8: 15
4. 3: 5

Solution: The compound ratio of 2: 3, 4: 5, and 7: 8 is (2 x 4 x 7): (3 x 5 x 8) = 56: 120 = 7: 15

∴ So the correct answer is 2. 7: 15

The compound ratio is 2. 7: 15

2. The approximate value of \(\frac{22}{7}\) to 3 places of decimals is

1. 3·142
2. 3.141
3. 3.145
4. 3.143

Solution: \(\frac{22}{7}\) = 3.1428…… ≈ 3.143

∴ The correct answer is 4. 3.143

3. If Anita takes 25 minutes to travel 2.5 km Anita’s speed is

1. 4 km/hr.
2. 5 km/hr.
3. 4.5 km/hr.
4. 6 km/hr.

Solution: In the mathematical language the problem is:

Time taken (min.)
25
60

Distance covered (km.)
2.5
?

According to the properties of the ratio proportion we get 25: 60 : : 2.5: Required distance.

Required distance is \(\frac{60 \times 2 \cdot 5}{25}=\frac{60 \times 25}{25 \times 10} \mathrm{~km}\) = 6 km

Speed is 6 km/hr.

∴ So the correct answer is 4. 6 km/hr

Anita’s speed is 4. 6 km/hr

Example 14. Write ‘True’ or ‘False’:

1. If the ratio of measurements of angles of a triangle is 1:2:3 then the triangle is a acute angled triangle.

Solution: The sum of the measurement of three angles of the triangle is 180°.

Let the measurements of three angles are x°, 2x°, and 3x°. [x is common multiple and x > 0]

x° + 2x° + 3x°= 180°

⇒ 6°x° = 180°⇒ x° = 30°

∴ The angles are 30°, 30° x 2 or 60° and 30° x 3 or 90°

So the triangle is right angled triangle.

∴ So the statement is false.

2. The difference between 1 and the approximate value of 0.9 to the integer is zero.

Solution: The approximate value of 0.9 to the integer is 1.

1 – 1 = 0

∴ So the statement is true.

Example 15. Fill in the blanks:

1. A ______ is a method to compare two quantities of the same kind having same unit.

Answer: Ratio.

2. 1 square metre = _______ square cm.

Answer: 1 square metre = 1 m x 1 m = 100 cm x 100 = 10000 sq.cm.

Coordinate Geometry Chapter 2 Internal And External Division Of Straight Line Segment

Concept of determination of a formula of coordinates of a point when a straight line segment is divided internally or externally in a given ratio.

1. Co-ordinates of the point P, which divides the line segment joining the points A (x₁, y₁) and B (x₂, y₂) internally in the ratio m:n are \(\left(\frac{m x_2+n x_1}{m+n}, \frac{m y_2+n y_1}{m+n}\right)\)

2. Co-ordinates of the point P, which divides the line segment joining the points A (x₁, y₁) and B (x₂, y₂) externally in the ratio m: n are \(\left(\frac{m x_2-n x_1}{m-n}, \frac{m y_2-n y_1}{m-n}\right)\)

Co-ordinate the midpoint P of the line segment joining two points A (x₁, y₁), B (x₂, y₂) are \(\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right)\)

Co-ordinates of the centroid of the triangle ABC where co-ordinates of A, B, C are (x₁, y₁),(x₂, y₂) and (x₃, y₃) respectively \(\left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}\right)\)

Read and Learn More  WBBSE Solutions For Class 9 Maths

Coordinate Geometry Chapter 2 Internal And External Division Of Straight Line Segment Fill In The Blanks

Example 1. The coordinates of the point which divides the line segment joining (6, – 4) and (-8, 10) in the ratio 3: 4 internally is _______

Solution: \(\left(0, \frac{-26}{7}\right)\)

Example 2. The coordinates of the midpoint of the line segment joining two points (5, 4), (3, -4) is _______

Solution: (4, 0).

Example 3. The ratio in which the point (1, 3) divides the line segment joining the points (4, 6), (3, 5) is ________ externally.

Solution: 32.

Example 4. The ratio at which the line segment joining the points (7, 3), (-9, 6) divides by Y axis is _______

Solution: 79.

Example 5. A (2, 3), B (9, 6), C (10, 12), and D (10, 12) are joined in order. ABCD is a _______

Solution: parallelogram.

Example 6. The points (3, 2), (6, 3), (x, y) and (6, 5) are joined in order to make a parallelogram (x, y) = _______

Solution: (9, 6).

Coordinate Geometry Chapter 2 Internal And External Division Of Straight Line Segment True Or False

Example 1. The Centroid of the triangle formed by the points (a – b, b – c), (-a, -b), (b, c) are (0, 0).

Solution: The statement is true.

Example 2. The coordinates of the point on the x axis at which the line segment joining the points (3, 4), (-3, -4) is bisected are (3, 0).

Solution: The statement is false.

Example 3. P is such a point on the line segment AB such that AP = PB. If A (-2, 4) and P (1, 5), then (4, 6).

Solution: The statement is true.

Example 4. The distance between two points on the x axis is 10 units. It origin the midpoint of these two points then the coordinates of the two point are (5, 0) and (-5, 0).

Solution: The statement is true.

Example 5. The coordinates of the point which divides the line segment joining the points (-1, 2), (2, -1) externally is 2 5 are (3, 4).

Solution: The statement is false.

Coordinate Geometry Chapter 2 Internal And External Division Of Straight Line Segment Short Answer Type Questions

Example 1. C is the centre of a circle and AB is the diameter, the coordinates of A and C are (6, -7) and (5, -2). Calculate the coordinates of B.

Solution: Let coordinates of B is (x, y)

∴ \(\frac{6+x}{2}=5 \Rightarrow x=4\)

∴ Co-ordinates are (4, 3).

∴  The coordinates of B is (4, 3).

Example 2. The points P and Q lie on 1st and 3rd quadrants respectively. The distance of the two points for x axis and y axis are 6 units, 4 units respectively. Find the midpoint of PQ.

Solution: Midpoint = \(\left(\frac{4-4}{2}, \frac{6-6}{2}\right)=(0,0)\)

The midpoint of PQ = \(\left(\frac{4-4}{2}, \frac{6-6}{2}\right)=(0,0)\)

Example 3. The point P lies on AB, AP = PB, the coordinates of A and B are (3, -4) and (-5, 2) respectively. Find their coordinates of P.

Solution: Coordinates of P = \(=\left(\frac{3-5}{2}, \frac{-h+2}{2}\right)=(-1,-1) .\)

Example 4. Points A and B lie on the 2nd and 4th quadrants. The distance of each point from x-axis and y-axis are 8 units and 6 units respectively. Write the coordinates of the midpoint of AB.

Solution: Midpoint of AB = \(\left(\frac{6+6}{2}, \frac{8-8}{2}\right)\) = (0, 0)

Example 5. The sides of a rectangle ABCD are parallel to the coordinates axes. Coordinates of B and D are (7, 3) and (2, 6). Write the coordinates of A, C and the midpoint of AC.

Solution: Absciss of C = Absciss of B = 7

∴ Co-ordinate of C is (7, 6)

⇒ Absciss of A = Absciss of A = 2

⇒ Ordinate of A = Ordinate of B = 3

⇒ Co-ordinates of A (2, 3)

⇒ Co-ordinates of midpoint of AC = \(\left(\frac{7+2}{2}, \frac{6+3}{2}\right)=\left(\frac{9}{2}, \frac{9}{2}\right)\)

Example 6. The coordinates of the vertices of a triangle are (4, -3), (-5, 2), (x, y). If the centroid of the triangle is at the origin, then find X, Y.

Solution: \(\frac{4-5+x}{3}=0 \Rightarrow x=1 \text { and } \frac{-3+2+y}{3}=0 \Rightarrow y=1\)

Example 7. Find the ratio in which the line segment joining the points (2, 3) and (5,- h) divided by x axis internally.

Solution: Let the coordinates at x-axis at which the line segment intersects i.e. (k, 0) and the ratio be m: n.

∴ \(\frac{-4 m+3 n}{m+n}\) =0 m: n = 3: 4

Example 8. Find the ratio in which the point (9, -23) divides the line segment joining (6, 4) and (7,-5)

Solution: Let the required ratio be m: n; 9 = \(\frac{7 n+6 n}{m+n}\) 9m + 9n = 7m + 6n

⇒ 2m = -3n, \(\frac{m}{n}=-\frac{3}{2}\)

∴ (9, -23) divides the line segment in 3: 2 externally.

Statistics Chapter 1 Statistics

Statistics may be defined as the science of collection, presentation, analysis, and interpretation of numerical data.

⇔ Data: Data are the collection of expressions or numbers by an individual or an institution for some purpose and are used by someone else in another context.

⇔ Variable: The changing numerical character is called a variable.

⇔  Example: Temperature in a day, and the daily expenditure of a family are variable.

Two types of variables:

1. Discrete variable,
2. Continuous variable

Example:

1. The number of members of a family, the temperature of the day, etc. are discrete variables.
2. The height and weight of students, etc. are continuous variables.

⇔  Attribute: In statistics the varying or changing quality is called an attribute.

Read and Learn More  WBBSE Solutions For Class 9 Maths

⇔  Range: The difference between the highest and lowest values of a given data is called range.

Example: From data 10, 12, 20, 35, 49, 15, 22, 48 the range is 49 – 10 = 39

⇔  Frequency: The number of times an observation occurs in the given data is called the frequency of the observation.

⇔  Class or class interval: The variables having extended range can be divided into a few classes. Each of these types of classes is called a class or class interval.

⇔  Class frequency: The number of values of a class included in a class is called class frequency.

⇔  Class-limit: The two end-values of the class interval is called class-limit.

The lesser value of the class limit in a particular class interval is called lower class limit and the larger value is called the upper-class limit of that class interval.

Example: In class 15-20 the lower limit is 15 and the upper limit is 20.

⇔  Class-boundary: The gaps of the class limits of any consecutive classes of statistical data are extended to the two limits, these two limits are called class-boundaries of those classes.

The lesser value is called the Lower class boundary and the greater value is called the Upper-class boundary.

Example: For classes 10-20, 20-30, 30-40,…, in class (20-30) the lower class boundary is 20, and the upper class boundary is 30.

In this class limit and class boundary are same.

Let the difference between the upper-class limit of a class and the lower-class limit of it is next class = d

Then in class (l₁ -l₂) the lower class boundary is \(\left(l_1-\frac{d}{2}\right)\) and the upper class boundary is \(\left(l_2+\frac{d}{2}\right)\).

Example: The class boundaries of classes 1-10, 11-20, 21-30, ……are 0.5 – 10.5, 10.5 – 20.5, 20.5 – 30.5

⇔  Class size or class length: The difference of the two class boundaries of a class is the class- size or class length.

∴ Class-size = Upper-class boundary – Lower class boundary.

In classes 0-10, 10-20, 20-30,…….., the class size of the class (20-30) is 10.

In classes 1-10, 11-20, and 21-30, the class size of class 21-30 is (30.5- 20.5) or 10

⇔  Midpoint or mid-value or class mark: The value of the variable that lies exactly at the middle of two class boundaries is called the Mid-value or class mark of that class.

The mid value of a class-interval

= \(\frac{\text { Upper class limit }+ \text { lower class limit }}{2}\)

= \(\frac{\text { Upper class-boundary }+ \text { lower class }- \text { boundary }}{2}\)

Example: The mid value of class (20-30) is \(\frac{20+30}{2} \text { or } \frac{50}{2} \text { or } 25\)

⇔  Relative frequency: The ratio of class frequency of a class and total frequency of any classified statistical data is called the relative frequency of that class.

Relative frequency =\(\frac{\text { Class }- \text { frequency }}{\text { Total frequency }}\)

⇔ Frequency density: The ratio of class frequency and the class size of the class in any classified data is called frequency density.

Frequency density of a class = \(\frac{\text { class frequency of that class }}{\text { class }- \text { size }}\)

⇔ Percentage frequency: When relative frequency is expressed in percentages, it is called percentage frequency.

Percentage frequency of a class = \(\frac{\text { class frequency of that class }}{\text { Total frequency }} \times 100\)

⇔  Cumulative frequency distribution: The frequency of the first class is added to that of the second and this sum is added to that of the third and so on, then the frequencies so obtained are known as Cumulative frequency.

When the cumulative frequency of each class in a frequency distribution table is shown, it is called a cumulative distribution table.

⇔  Two types of cumulative frequency distribution table are constructed:

1. Less than type cumulative frequency: The new frequencies were obtained by adding class frequencies successively in the above frequency distribution table.
2. This type of frequency distribution table is called less than type cumulative frequency distribution table.
3. More than type cumulative frequency distribution table: The new frequencies are obtained by adding class frequencies successively from the below frequency distribution table.

This type of frequency distribution table is called more than the type of cumulative frequency distribution table.

Histogram: The graphical representation of a classified frequency distribution of continuous variables is called Histogram.

Frequency polygon: A frequency polygon is the graphical representation of a frequency distribution that is expressed through the classes of equal size of a continuous variable.

Statistics Chapter 1 Statistics True Or False

Example 1. Relative frequency is determined by class frequency and class length.

Solution: Relative frequency of a class = \(=\frac{\text { frequency of that class }}{\text { total frequency }}\)

So if total frequency are not given then it is impossible so determine the relative frequency.

∴ The statement is False.

Example 2. In classes 6-10, 16-20, 26-30,……, the lower class boundary of the second class is 13

Solution: The difference between the first two class is (16 – 10) or 6

Lower class boundary of the second class is 916 – \(\frac{6}{2}\) or 13

∴ The statement is True.

Statistics Chapter 1 Statistics Fill In The Blanks

Example 1. For the construction of the histogram, the values of the ________ variable are taken along X-axis

Solution: Continuous.

[If discontinuous variables are given then firstly it is converted into a continuous class boundary]

Example 2. For the construction of a frequency polygon, the values included in a class are concentrated at the _______ of the corresponding class.

Solution: midpoint.

Statistics Chapter 1 Statistics Short Answer Type Questions

Example 1. In a continuous frequency distribution table if the mid-point of a class is m and the upper class boundary is m, then find out the lower class boundary.

Solution: Let the lower class boundary of the class is n.

The upper-class boundary is u

∴ The midpoint of that class is \(\frac{x+u}{2}\)

According to question \(\frac{x+u}{2}\) = m

⇒ n + u = 2m

⇒ x = 2m – u

∴ The lower class boundary is (2m – u)

Example 2. In a continuous frequency distribution table, if the mid-point of a class is 42 and class size is 10, then write the upper and lower limit of the class.

Solution: Let the upper limit is a and lower limit is b

∴ The mid-point is \(\frac{a+b}{2}\) and class size is (a – b)

According to question, \(\frac{a+b}{2}\) = 42

⇒ a + b = 84 ……(1)

and a – b = 10…..(2)

(1) + (2) we get, a + b + a – b = 84 + 10

⇒ 2a = 94

a = \(\frac{94}{2}\)= 47

∴ b = 84 – 47 = 37

∴ The upper and lower limit of the class are 47 and 37 respectively.

Example 3.

Find the frequency density of the first class of the above frequency distribution table.

Solution: The difference between the two consecutive class is 1

∴ The lower-class boundary and upper-class boundary of the first class are (70 – \(\frac{1}{2}\)) = 69.5 and (74 – \(\frac{1}{2}\)) = 74.5 respectively.

Class size 74.5 – 69.5 = 5

The frequency density = \(\frac{\text { frequency of the } 1 \text { st class }}{\text { class size }}=\frac{3}{5}=0.6\)

Example 4.

Find the relative frequency of the last class of the above frequency distribution table.

Solution: Relative frequency of last class = \(\frac{\text { frequency of that class }}{\text { Total frequency }}=\frac{8}{20}=0.4\)

Example 5. Write from the following examples which one indicates attribute and which one indicates variable.

1. The population of the family
2. Daily temperature
3. Educational value
4. Monthly income are not fixed.
5. Grade obtained in Madhyamik Examination.

Solution:

1. The population of the family are always changeable. So it is variable.
2. Daily temperature is always changeable, it is a variable.
3. Educational value indicate attribute.
4. Monthly income are not fixed. It is a variable.
5. Grade obtained in Madhyamik Examination are indicates attributes.

Example 6. Given below are the marks obtained by 40 students in Bengali in an Examination of School.

Construct a frequency distribution table for the above-given data.

Solution:

Example 7. Construct a frequency distribution table from the following cumulative frequency: distribution table, given below

Solution:

Example 8. In a frequency distribution table, the mid-value of five classes are 15, 20, 25, 30, and 35, and their corresponding frequency are 2, 4, 3, 6, and 8 respectively; prepare a frequency distribution table for the construction of the Histogram.

Solution: The difference of mean value between two consecutive class

= 20 – 15 = 25 – 20 = 30 – 25 = 35 – 30 = 5

The lower-class boundary and upper-class boundary of the first class are (15-\(\frac{5}{2}\)) or 12.5 and (15+\(\frac{5}{2}\)) or 17.5

So, the frequency distribution table are given below:

Example 9. The distribution of height (in cm) of 20 students is given below. Construct a histogram.

Solution:

Example 10. Draw the frequency polygon for the frequency distribution table given below:

Solution: The midpoint of given classes are \(\frac{60+70}{2}, \frac{70+80}{2}, \frac{80+90}{2}, \frac{90+100}{2}\) or, 65, 75, 85, 95.

Coordinate Geometry Chapter 1 Distance Formulas

⇒ Coordinate Geometry: The branch of mathematics in which different problems of geometry are solved with the help of algebra is known as coordinate geometry.

⇒ Two types of co-ordinate geometry:

1. Two-dimensional or plane geometry.
2. Three-dimensional or solid geometry.

⇒  XOX’ and YOY’ are two perpendicular straight lines intersects at O.

⇒  They have divided the plane into four sections. Each of these sections is called a quadrant.

⇒  The section XOY, YOX’, X’OY’, and Y’OX’ are called the 1st, 2nd, 3rd, and 4th quadrants respectively.

⇒  The fixed point O is called the origin whose coordinate is (0, 0).

⇒  The straight lines together are called the coordinate axes.

⇒  \(\overleftrightarrow{\mathrm{XOX’}}\) is called the x-axis or abscissa and \(\overleftrightarrow{\mathrm{YOY’}}\) is called the y-axis or ordinate.

Read and Learn More  WBBSE Solutions For Class 9 Maths

Formulas at a glance:

1. Distance of a given point P(x, y) from the origin (0, 0) is OP = \(\sqrt{x^2+y^2}\)
2. The distance between two given points P (x₁, y₁) and Q (x₂, y₁) is \(\overline{P Q}=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\) units.

Coordinate Geometry Chapter 1 Distance Formulas True Or False

Example 1. The distance between the points A(a, 0) and B(b, 0) along the positive direction of the X-axis is (b – a) units (b > a).

Solution: The distance between the points A(a, 0)

and B (b, 0) is \(\sqrt{(b-a)^2+(0-0)^2}\) units

= \(\sqrt{(b-a)^2}\) units

= (b – a) units

∴ The statement is True.

Example 2. The distance between two points A(-p, 0) and (-q, 0) along the negative direction of X- axis (p – q) units [p < q].

Solution: The distance between A(- p, 0) and B(-q, 0) is

\(\sqrt{\{-q-(-p)\}^2+(0-0)^2}\) units

= \(\sqrt{(-q+p)^2}\) units

= \(\sqrt{{-(q-p)}^2}\) units

= \(\sqrt{(q-p)^2}\) units =(q – p) units

∴ The statement is False.

Example 3. The points (3, 4) and (-3, -4) are equidistant from origin.

Solution: The distance of point (3, 4) from origin (0, 0) is \(\sqrt{3^2+4^2}\) units = √25 units = 5 units

The distance between points (-3, -4) and (0, 0) is \(\sqrt{(-3)^2+(-4)^2}\) units

= \(\sqrt{9+16}\) units = √25 units = 5 units

∴ The statement is True.

Coordinate Geometry Chapter 1 Distance Formulas Fill In The Blanks

Example 1. The distance between the points A (0, m) and (0, – n) is _______ units.

Solution: The required distance is \(\sqrt{(0-0)^2+\{m-(-n)\}^2}\) units = \(=\sqrt{(m+n)^2}\) units = (m + n) units.

Example 2. The distance between the points (-7, 0) and (-2, 0) is ________ units.

Solution: The required distance is \(\sqrt{\{(-7)-(-2)\}^2+(0-0)^2}\) units

= \(\sqrt{(-7+2)^2+0} \text { units }\)

= \(\sqrt{(-5)^2} \text { units }\)

= √25 units = 5 units.

Example 3. If in a square (4, 4) and (-4, 4) are two adjacent vertices, then the perimeter of the square is ______ units.

Solution: The length of AD is \(\sqrt{(-4-4)^2+(4-4)^2}\) units

= \(\sqrt{(-8)^2+(0)^2}\) units

= √64 units = 8 units

Perimeter is (4 x 8) units= 32 units.

∴ The perimeter of the square is 32 units.

Coordinate Geometry Chapter 1 Distance Formulas Short Answer Type Questions

Example 1. Find the value of y if the distance of the point (-4, y) from origin is 5 units.

Solution: The distance of the point (-4, y) from the origin (0, 0) is \(\sqrt{(-4-0)^2+(y-0)^2}\) units

= \(\sqrt{16+y^2}\) units

According to question, \(\sqrt{16+y^2}\) = 5

⇒ 16 + y² = 25

⇒ y² = 25 – 16

⇒ y² = 9

⇒ y = ±√9

⇒ y = ±3

∴ The value of y is ±3.

Example 2. Find the coordinates of a point on the y-axis which is equidistant from two points (2, 3) and (-1, 2).

Solution: Let the coordinates of a point of the y-axis is (0, k)

The distance between the points (2, 3) and (0, k) is \(\sqrt{(2-0)^2+(3-k)^2}\) units

The distance between the points (1, 2) and (0, k) is \(\sqrt{(-1-0)^2+(2-k)^2}\) units

According to question, \(\sqrt{(2-0)^2+(3-k)^2=\sqrt{(-1-0)^2+(2-k)^2}}\)

⇒ 4 + (3 – k)² ⇒ 1 + (2 – k)² [squaring both sides]

⇒ 4 + 9 – 6k + k² = 1 + 4 – 4k + k²

⇒ -6k + k² + 4k – k² = 5 – 4 – 9

⇒ -2k = -8

⇒ k = 4.

∴ The coordinate of points on the Y-axis is (0, 4).

Example 3. Write the coordinates of two points on X-axis and Y-axis for which an isosceles right-angled triangle is formed with x-axis, y-axis, and straight line. joining two points.

Solution: As an isosceles right-angled triangle is formed with the x-axis, y-axis, and a straight line joining two points A and B;

∴ OA = OB

∴ The coordinates of two points on X-axis and Y-axis are (1, 0), (0, 1); (2, 0), (0, 2); (3, 0), (0, 3), etc.

Example 4. Write the coordinates of two points on opposite sides of x-axis which are equidistant from x-axis.

Solution: The coordinates of two points on opposite sides of x-axis are (2, 3), (2, -3); (-5, 6), (-5, -6) etc.

Example 5. Write the coordinates of two points on opposite sides of y-axis which are equidistant from y-axis.

Solution: The coordinates of two points on opposite sides of y-axis which are equidistant from y-axis are (2, 5), (-2, 3); (4, 6), (-4, 8) etc.

Example 6. Show that point (-2, -11) are equidistant from points (-3, 7) and (4, 6).

Solution: The distance between the points (-2, -11) and (- 3, 7) is \(\sqrt{\{-2-(-3)\}^2+(-11-7)^2} \text { units }\)

= \(\sqrt{(-2+3)^2+(-18)^2} \text { units }\)

= \(\sqrt{1+324} \text { units }=\sqrt{325} \text { units }\)

The distance between the points (-2, -11) and (4, 6) is \(\sqrt{(-2-4)^2+(-11-6)^2}\) units

= \(\sqrt{(-6)^2+(-17)^2} \text { units }\)

= \(\sqrt{36+289} \text { units }=\sqrt{325} \text { units }\)

∴ The point (-2,-11) is equidistant from points (-3, 7) and (4, 6).

Example 7. If the points A (2, -2), B (8, 4), C (5, 7), and D(-1, 1) are the vertices of a rectangle, then show that the lengths of diagonals AC and BD are equal.

Solution: The length of diagonal AC is \(\sqrt{(2-5)^2+(-2-7)^2} \text { units }\)

= \(\sqrt{(-3)^2+(-9)^2} \text { units }\)

= \(\sqrt{9+81} \text { units }=\sqrt{90} \text { units }\)

The length of diagonal BD is \(\sqrt{\{8-(-1)\}^2+(4-1)^2}\) units

= \(\sqrt{(9)^2+(3)^2}\) units

= \(\sqrt{81+9}\) units

= \(\sqrt{90}\) units

∴ AC = BD.

Example 8. Are the points A (0, 0), B (4, 3), and C (8, 6) co-linear? Verify the statement.

Solution: If A, B, and C are co-linear then AB + BC = AC

AB = \(\sqrt{(4-0)^2+(3-0)^2} \text { units }=\sqrt{25} \text { units }=5 \text { units }\)

BC = \(\sqrt{(8-4)^2+(6-3)^2} \text { units }\)

= \(\sqrt{16+9} \text { units }=\sqrt{25} \text { units }=5 \text { units. }\)

AC = \(\sqrt{(8-0)^2+(6-0)^2} \text { units }\)

= \(\sqrt{100} \text { units }=10 \text { units }\)

∴ AB+ BC= (5 + 5) units = 10 units

∴ AB + BC = AC

∴ The given points are co-linear.

Example 9. If the distance between the points (2, y) and (10,-9) is 10 units then find the value of y.

Solution: The distance between the points (2, y) and (10, -9) is \(\sqrt{(2-10)^2+\{y-(-9)\}^2} \text { units }\)

= \(\sqrt{64+(y+9)^2} \text { units }\)

According to question, \(\sqrt{64+(y+9)^2}\) = 10

⇒ 64 + y² + 18y + 81 = 100

⇒ y² + 18y + 45 = 0

⇒ y + 15y + 3y + 45 = 0

⇒ y (y + 15) + 3 (y + 15) = 0

⇒ (y + 15) (y + 3) = 0

either y + 15 = 0

⇒ y = – 15

or, y + 3 = 0

⇒ y = – 3

∴ The value of is – 3.

Example 10. Find the point on X-axis which are equidistant from points (3, 5) and (1, 3).

Solution: Let the point on X-axis is (h, 0)

The distance between (3, 5) and (h, 0) is \(\sqrt{(3-h)^2+(5-0)^2}\) units

The distance between (1, 3) and (h, 0) is \(\sqrt{(1-h)^2+(3-0)^2}\) units

According to question, \(\sqrt{(3-h)^2+(5-0)^2}=\sqrt{(1-h)^2+(3-0)^2}\)

⇒ 9 – 6h + h² + 25 = 1 – 2h + h² + 9

⇒ -6h + 2h + h² – h² = 1 + 9- 9 – 25

⇒ – 4h = – 24 ⇒ h = 6

∴ The required points is (6, 0).

Coordinate Geometry Chapter 3 Area Of Triangular Region

Area of formula:

1. The area of ΔABC where vertices are A (x₁, y₁), B (x₂, y₂) and C (x₃, y₃) respectively is \(\frac{1}{2}\left|x_1\left(y_2-y_3\right)+x_2\left(y_3-y_1\right)+x_3\left(y_1-y_2\right)\right|\) sq. unit

or, = \(\frac{1}{2}\left|y_1\left(x_2-x_3\right)+y_2\left(x_3-x_1\right)+y_3\left(x_1-x_2\right)\right|\) sq. unit [Area is always taken positive]

2. The points (x₁, y₁), (x₂, y₂), (y₃, y₃) are collinear if x₁ (y₂ – y₃)+ x₂ (y₃ – y₁) + x₃ (y₁ – y₂) = 0

or, y₁ (x₂ – x₃) + y₂ (x₃ – x₁) + y₃(x₁ – x₂) = 0

Read and Learn More  WBBSE Solutions For Class 9 Maths

Area of the triangular region is

= \(\frac{1}{2}=\left|x_1 y_2+x_2 y_3+x_3 y_1-\left(y_1 x_2+y_2 x_3+y_3 x_1\right)\right|\) sq. unit

Similarly, area of quadrilateral region is

= \(\frac{1}{2}\left|\left(x_1 y_2+x_2 y_3+x_3 y_4+x_4 y_1\right)-\left(y_1 x_2+y_2 x_3+y_3 x_4+y_4 x_1\right)\right|\) sq. unit

Coordinate Geometry Chapter 3 Area Of Triangular Region Fill In The Blanks

Example 1. Area of the triangle having vertices (2, 2), (4, 2), (1, 3) is _______ sq. unit.

Solution: 11

Example 2. (0, -2), (2, 4), (-1, -5) are ______ points.

Solution: Collinear.

Example 3. If (2, -1), (k, -1), (1, -1) are collinear points then k = ________

Solution: Any real value.

Example 4. If the points (1, 2), (2, 4), and (6, 6) are collinear then t = 

Solution: 3

Example 5. If the vertices of a triangle are (-1, 0), (0, 0), (0, 1) then its area is ______ sq. unit

Solution: \(\frac{1}{2}\)

Example 6. If the three points (0, 0), (2, -3), (x, y) are collinear then x = ______, y = _______

Solution: 4, -6.

Coordinate Geometry Chapter 3 Area Of Triangular Region True Or False

Example 1. Area of the triangle having vertices (-3, 1), (– 2, 2), and (3, 2) is 9\(\frac{1}{2}\) sq. unit.

Solution: The statement is true.

Example 2. If the vertices of a triangle are (a, b + c), (a, b – c), and (-a, c) then area is \(\frac{1}{2}\)/ab/sq.unit

Solution: The statement is false.

Example 3. (1, 4), (-1, 2), (-4, -1) are collinear points.

Solution: The statement is true.

Example 4. (a, b + c), (b, c + a), (c, a + b) are not collinear points.

Solution: The statement is false.

Example 5. Value of k for which (k, k), (-1, 5), (-7, 8) be collinear is 3.

Solution: The statement is true.

Example 6. If the points (a, c), (0, b), (\(\frac{1}{2}\), \(\frac{1}{2}\)) are collinear points then \(\frac{1}{a}+\frac{1}{b}=2\)

Solution: The statement is false.

Coordinate Geometry Chapter 3 Area Of Triangular Region Short Answer Type Questions

Example 1. If the three points (a, 0), (0, b), (1, 1) are collinear then show that \(\frac{1}{a}+\frac{1}{b}=1\)

Solution:

= \(\frac{1}{2}|a b+0+0-b-a|=0 \quad \text { or, } a+b=a b\)

∴ \(\frac{1}{a}+\frac{1}{h}=1\)

Example 2. Find the area of the triangular area region formed by the three points (1, 4), (-1, 2), and (-4, 1).

Solution:

⇒ Area = \(\frac{1}{2}|2-1-16+4+8-1| \text { sq.unit }=\frac{1}{2}|14-18| \text { sq.. unit }=2\)

The area of the triangular area region = \(\frac{1}{2}|2-1-16+4+8-1| \text { sq.unit }=\frac{1}{2}|14-18| \text { sq.. unit }=2\)

Example 3. If the points (0, -4), (-1, y), and (3, 2) are on the same straight line find y.

Solution: \(\frac{1}{2}|0(y-2)+(-1)\{2-(-4)\}+3(-4-4)|=0\)

⇒ or, -6 – 12 – 3y = 0, y = 6

Example 4. If the points A (3a, k), B (0, 3b), C (a, 2b) are collinear find k.

Solution: 3a (3b – 2b) + 0 (2b – k) + a (k – 3b) = 0

or, 3ab + ak – 3ab 0 or, ak = 0

∴ k = 0

Example 5. Show that (a, b + c), (b, c + a), and (c, a + b) are collinear.

Solution: \(\frac{1}{2}\left|x_1\left(y_2-y_3\right)+x_2\left(y_3-y_1\right)+x_3\left(y_1-y_2\right)\right|\)

= \(\frac{1}{2}[a(c+a-a-b)+b(a+b-b-c)+c(b+c-c-a)]\)

= \(\frac{1}{2}(a c-a b+a b-b c+b c-a c)=0\)

⇒ Here x₁ = a, y₁ = b + c

⇒ x₂ = b, y₂ = c + a.

⇒ x₃ = c, y₃ = a + b

Example 6. If A (x, 4), B (- 5, 7), C (-4, 5) are collinear, then show that 2x+y+3=0

Solution: \(\frac{1}{2}\)[x(7-5) + (-5)(5 − y) + (−4)(y −7)] = 0

⇒ or, \(\frac{1}{2}\)(2x+y+3)=0

∴  2x + y + 3 = 0

Mensuration Chapter 3 Area Of Circle

⇔ Area of circle = πr²

⇔ Area of semi-circle = \(\frac{1}{2}\) πr²

⇔ Area of circular ring = π (R² – r²) = π (R + r)(R -r)

Read and Learn More  WBBSE Solutions For Class 9 Maths

⇔ Sector of a circle = \(\pi r^2 \cdot \frac{\theta}{360}\)

⇔ Area of a square inscribed in a circle = \(\frac{(\text { diagonal })^2}{2}=\frac{(2 r)^2}{2}=2 r^2\)

⇔ Area of a square circumscribing the circle = (2r)² = 4r²

⇔ Area of an equilateral triangle, when the length of the radius of its in circle = r unit

⇔ Area of the triangle = \(\frac{\sqrt{3}}{4}(2 \sqrt{3} r)^2=3 \sqrt{3} r^2\)

⇔ Area of an equilateral triangle, when the length of the radius of its circumcircle is r unit

⇔ Area of the triangle = \(\frac{\sqrt{3}}{4}(4 \sqrt{3} r)^2=12 \sqrt{3} r^2\)

Mensuration Chapter 3 Area Of Circle Fill In The Blanks

Example 1. If the circumference of a circle be 22 cm, then its area will be ______ sq. cm

Solution: 38.5.

Example 2. The area of a sector making an angle 30° at the centre of a circle of radius 21 cm is ______ sq. cm.

Solution: 115.5.

Example 3. If the ratio of the circumference of two circles be 2: 3, the ratio of their areas will be ______

Solution: 4:9.

Example 4. If x be the area of a circle its circumference is ______

Solution: 2√πx

Example 5. The diameter of a circle inscribed in the square of area 49 sq cm is ______

Solution: 7 cm.

Mensuration Chapter 3 Area Of Circle True Or False

Example 1. If the circumference of a circle is A, then its diameter = \(\frac{A}{\pi}\).

Solution: The statement is true.

Example 2. The radius of a circle is 21 cm, its area is 616 sq. cm.

Solution: The statement is false.

Example 3. Area of a semi-circle of radius 7 cm is 77 cm.

Solution: The statement is true.

Example 4. When a square is inscribed in a circle, its diagonal will be equal to the diameter of the circle.

Solution: The statement is true.

Example 5. When a square circumscribed a circle, its diagonal will be equal to the diameter of the circle.

Solution: The statement is false.

Mensuration Chapter 3 Area Of Circle Short Answer Type Questions

Example 1. If the length of radius of a circular field was increased by 10%, let us write by calculating what % it increase the area.

Solution: Let radius = 100 r unit

Initial Area = 10000 πr² sq.unit

Increased Area = π(110)² sq.unit = 12100 πr² sq.unit

% increase = \(\frac{2100 \pi r^2}{10000 \pi r^2}\) x 100 sq.unit = 21 sq.unit

∴ 21% increased.

Example 2. If the perimeter of a circular field was decreased by 50%. Calculate what percent it decrease the area of circular field.

Solution: Let radius be r unit.

Initial perimeter and area = 2πr unit, πr²sq.unit

Reduced perimeter = \(\frac{2 \pi r}{2}\) unit = πr unit

Reduced radius = \(\frac{r}{2}\) unit

Area decrease = \(=\left\{\pi r^2-\pi\left(\frac{r}{2}\right)^2\right\} \text { sq. unit }=\frac{3 \pi r^2}{4} \text { sq. unit }\)

∴ % decrease = \(\frac{3 \frac{\pi r^2}{4}}{\pi r^2}\) x 100 sq.unit = 75%

Area is decreased by 75%.

Example 3. The length of radius of a circular field is r meter. If the area of other circle is x times of first circle, let us calculate how length of radius of other circle.

Solution: Area = x x πr²

πR² = πr²

∴ R= r√x unit.

Example 4. Calculate the area of a circular region circumscribe a triangle of which sides are 3 cm, 4 cm, and 5 cm.

Solution: 3²+ 4² = 5², It is a right-angled triangle.

Length of circumradius = \(\frac{5}{2}\) cm = 2.5 cm.

Area = \(\frac{22}{7}\) x 2.5 x 2.5 sq.cm = 19\(\frac{9}{14}\) sq.cm.

Example 5. Three circular plates were cut off from a tin plate with equal width if the ratio of the length of diameter of three circles is 3: 5: 7, calculate the ratio of their weight.

Solution: Let weight of per sq. unit tin = x gm

Let diameter be 3R, 5R, 7R units respectively (R > 0)

∴ Ratio weight = \(\pi\left(\frac{3 \mathrm{R}}{2}\right)^2 \cdot x: \pi\left(\frac{5 \mathrm{R}}{2}\right)^2 \cdot x: \pi\left(\frac{7 \mathrm{R}}{2}\right)^2 \cdot x\) = 9: 25: 49

Example 6. Find the area of the shadow region of the figure.

Solution: Area =\(\left\{\frac{90}{360} \pi \cdot(14)^2-\Delta A O B\right\} \mathrm{sq} \cdot \mathrm{cm}\)

= \(\left\{\frac{1}{4} \pi \cdot(14)^2-\frac{1}{2} \cdot 14 \cdot 14\right\} \mathrm{sq} \mathrm{cm}=56 \mathrm{sqcm}\)

Example 7. If the perimeter of a circle = perimeter of an equilateral triangle. Find the ratio of their areas.

Solution: 2πr = 3a  ⇒ r = \(\frac{3a}{2 \pi}\)

∴ Ratio = \(\pi\left(\frac{3 a}{2 \pi}\right)^2: \frac{\sqrt{ } 3}{4} a^2=63: 22 \sqrt{3}\)

Example 8. Find The area of the shadow region of

Solution: Area = Area of the square – Area of 4 sectors

= \(\left\{12^2-\frac{90^{\circ}}{360^{\circ}} \times \pi(6)^2 \times 4\right\} \mathrm{sq} \cdot \mathrm{cm}=30 \frac{6}{7} \mathrm{sq} . \mathrm{cm}\)

Example 9. Find the area of shadow region of

Solution: Area Of 4 setors

= \(\left\{\frac{22}{7} \times(3.5)^2\right\}-\left\{\frac{90^{\circ}}{360^{\circ}} \times \frac{22}{7} \times(3.5)^2\right\} \times 4 \text { sq.cm }=115.5 \text { sq.cm }\)

Example 10. Find the area of the shadow region of

Solution: Area = \(\left(\frac{1}{4} \times \frac{22}{7} \times 12^2-\frac{1}{2} \times 12 \times 12\right) \mathrm{sqcm}\)

= \(\frac{288}{7} \text { sq. }\)

= \(41 \frac{1}{7} \text { sq. } \mathrm{cm}\)

Mensuration Chapter 2 Circumference Of Circle

Some Important Facts:

In any circle:

\(\frac{Circumference}{Diameter}\) = constant (denoted by π and π = \(\frac{22}{7}\))

Read and Learn More  WBBSE Solutions For Class 9 Maths

∴ circumference = π x diameter = π x 2 x radius

= πd = 2πr (d = length of the diameter, r = length of the radius)

Circular ring:

Let length of the inter radius and length of outer radius = R

∴ The width of the ring = R – r.

Mensuration Chapter 2 Circumference Of Circle True Or False

Example 1. If the circumference of a circle is A cm, then its radius is \(\frac{A}{\pi}\) cm.

Solution: 2πr = A

⇒ r = \(\frac{A}{2 \pi}\)

∴ The statement is False.

Example 2. The difference of the circumference and the radius is 3.7 cm. Length of its diameter is 1.4 cm.

Solution: 2πr – R = 3.7

⇒ R(2π – 1) = 3.7

⇒ R = \(\frac{3.7 \times 7}{37}\) =0.7, 2R = 1.4 cm

∴ The statement is True.

Example 3. The width of a circular ring is 7 cm. The difference between the outer and inner circumference of the ring is 4.4 cm.

Solution: R – r = 7

∴ 2π (R – r) = 7 x 2 x \(\frac{22}{7}\) = 44

∴ The statement is False.

Example 4. Perimeter of a semi-circular ring is π (R + r) + 2(R – r) when R and r are the length of outer and inner radius.

Solution: Perimeter Outer semi-circumference + inner circumference + 2 (width)

= πR + πr + 2 (R – r)

∴ The statement is True.

Example 5. The outer and inner circumference of a ring-shaped circular plate are x cm and y cm respectively. The width of the ring-shaped plate is \(\frac{x-y}{\pi}\) cm.

Solution: 2πR – 2πr = x – y

or, R – r = \(\frac{x-y}{2 \pi}\)

∴ The statement is False.

Mensuration Chapter 2 Circumference Of Circle Fill In The Blanks

Example 1. If the circumference of a circle be 44 cm, then its length of the diameter is ________ cm.

Solution: 14.

2πr = 44 ⇒ 2r = \(\frac{44 \times 7}{22}\) = 14

Example 2. In radius of an equilateral triangle is 7 cm, so the measure of its circumradius is _______ cm.

Solution: 14 cm.

∴ \(\frac{\sqrt{3}}{2} \times \frac{2}{3}=21 \times \frac{2}{3} \mathrm{~cm}=14 \mathrm{~cm}\)

Example 3. The circumference of a circular wheel is 250 dm. The no. of revolution to move 1 km is _______

Solution: 30.

No. of revolution \(\frac{10000}{250}=30\)

Example 4. A circular wheel revolves 80 times to 8088 m. Circumference is _________

Solution: 110 cm.

Circumference = \(\frac{88}{80}\) m = 1.1 m = 110 cm.

Example 5. The diameter of a circular wheel is 3.5 mt. The distance which is carved by 1400 revolution _______

Solution: 15.4 km.

Distance covered = 1400 circumference = 1400 x \(\frac{22}{7}\) x 3.5 mt = 15.4 km

Mensuration Chapter 2 Circumference Of Circle Short Answer Type Questions

Example 1. If the perimeter of a semicircle is 180 m. Find its diameter.

Solution: If the length of the radius is r m then πr + 2r = 180

or, \(r\left(\frac{22}{7}+2\right)=180\)

or, r = \(\frac{180 \times 7}{36} \times 35 \mathrm{~m}\)

or, 2r = 70m

∴ Its diameter = 70 m.

Example 2. The length of a minute’s hand is 7 cm. How much length will Minute’s hand go to rotate 90°?

Solution: Length = \(\frac{\text { angle of centre }}{360^{\circ}}\) x circumference

= \(\frac{90^{\circ}}{360^{\circ}}\) x 2π x 7 cm = 11 cm

∴ 11 cm much length will minute hand go to rotate.

Example 3. What is the ratio of radii of the inscribed and circumscribed circle of a square?

Solution: Let length of the side of the square be a unit

Length of the circumradius = \(\frac{1}{2}\) diagonal of the square

= \(\frac{\sqrt{2}}{2}\) a unit

∴ Length of the inradius = \(\frac{1}{2}\) length of the side = \(\frac{a}{2}\)

ratio = \(\frac{a \sqrt{ } 2}{2}: \frac{a}{2}\) = √2:1

∴ The ratio of radii of the inscribed and circumscribed circle of a square.

Example 4. The minute’s hand of a clock is 7 cm. How length does the minute’s hand move is 15 minutes?

Solution: circumference = 2 x \(\frac{22}{7}\) x 7 cm = 44 cm

Now minute’s hand covers 44 cm in 60 minutes.

∴ In 15 minutes it covers \(\frac{44}{60}\) x 15 = 11 cm.

Example 5. What is the ratio of perimeter of a square and perimeter of a circle when the length of diameter of circle is equal to the length of the side of the square.

Solution: d = a (d is the length of the diameter and a is the length of the side of the square)

∴ Ratio = 4a: πd

= 4а: πа (d = a)

= 4 : π = 4 x 7: 22 = 14: 11

∴ The ratio of perimeter of a square and perimeter of a circle is 14: 11.

Example 6. A wire of length 36 cm is made a semi-circle. Find its length of the radius.

Solution: R (π + 2) = 36

(Length of the radius is R cm)

or, \(\frac{36 R}{7}\) = 36

⇒ R = 7 cm.

∴ The length of the radius is 7 cm.

Example 7. Circumference of a wheel is 2 m 5 dem. If the speed is 15 km/hr find the revolution of the wheel per minute.

Solution: Circumference = 25 dcm.

In 60 minute wheel covers 15 km = 150000 dcm

In 1 minute wheel covers \(\frac{150,000}{60}\)dcm = 2500 dcm

∴ No. of revolution per minute = \(\frac{2500}{25}\) = 100 dcm

∴ The revolution of the wheel per minute is 100 dcm.

Example 8. Ratio of the circumference of two circles is 2: 3 and difference of the length of radii is 2 cm. Find the smaller radius.

Solution: Let length of the smaller radius r cm.

∴ Length of bigger radius = (r + 2) cm

∴ \(\frac{2 \pi r}{2 \pi(r+2)}=\frac{2}{3}\)

⇒ 3r = 2r + 14

∴ r = 4 cm

∴ The smaller radius is 4 cm.

Example 9. If the circumference is 2π² unit, then find its diameter.

Solution: 2πr = 2π² ⇒ 2r = 2π

∴ Length of the diameter = 2π unit.

Example 10. The circumference of a circles is 22 cm. Then find the length of the diagonal of a square inscribed in that circle.

Solution: Let length of the radius be r cm circumference 2πr = 22 cm

∴ 2 x \(\frac{22}{7}\) x r = 22

or, r = \(\frac{7}{2}\)

Length of the side of the square = Diameter of the circle = \(\frac{7}{2}\) x 2 cm = 7 cm

∴ Length of the diagonal of the square = √2 x 7 cm = 7√2 cm.

Mensuration Chapter 1 Area And Perimeter Of Triangle And Quadrilateral Useful Information And Formulae

Rectangle:

Let the length of a rectangle be a units and its breath be is units.

1. Area of the rectangle = lengths x breadth = ab sq units. ∴ length = \(\frac{\text { area }}{\text { breadth }}\); breadth = \(\frac{\text { area }}{\text { length }}\)
2. Perimeter of the rectangle 2 (length + breadth) = 2(a + b) units ∴ length breadth = semi perimeter.
3. Diagonal of the rectangle = \(\sqrt{(\text { length })^2+(\text { breadth })^2}=\sqrt{a^2+b^2} \text { units. }\)

Square:

Let each side of a square be a units

1. Area of the square = a² sq. units.
2. Perimeter of the square = 4a units ∴ side = \(\frac{\text { perimeter }}{4}\)
3. Diagonal of the square = a√2 units ∴ area of the square = \(\frac{1}{2}\) (diagonal)².

Read and Learn More  WBBSE Solutions For Class 9 Maths

Rhombus:

1. Area of the rhombus = \(\frac{1}{2}\) x product of the diagonals base x height.
2. Perimeter of the rhombus = 4 x side.

Trapezium and parallelogram:

1. Area of the trapezium = \(\frac{1}{2}\) x sum of the distance of the parallel side between them.
2. Area of the parallelogram = base × height.
3. Area of the four walls of a rectangular room = Perimeter of the floor x height of the room = 2 (lengths + breadth) x height.

Triangle:

Let the sides of a triangle be a units, b units and c units.

1. Area of the triangle = \(\frac{1}{2}\) x base x height.
2. Area of the triangle = \(\sqrt{\mathrm{S}(s-a)(s-b)(s-c)}\) sq units. where S semi-perimeter of the triangle = \(\frac{1}{2}\) (a+b+c) units.
3. Height of the equilateral triangle = \(\frac{\sqrt{3}}{2}\) x side
4. Median of the equilateral triangle = height of that triangle.
5. Circum radius of the equilateral triangle = \(\frac{2}{3}\) x median.
6. In radius of the equilateral triangle = \(\frac{1}{3}\) x median.
7. Area of the equilateral triangle = \(\frac{\sqrt{3}}{4}\) x (side)².
8. If the base of an isosceles triangle be a units and each of the two equal sides of b units, then height of that isosceles triangle \(\sqrt{b^2-\frac{a^2}{4}}\) units and area of that isosceles triangle = \(\frac{1}{2} \times a \times \sqrt{b^2-\frac{a^2}{4}}\) units.

Mensuration Chapter 1 Area And Perimeter Of Triangle And Quadrilateral Useful Information And Formulae Fill In The Blanks

Example 1. The length of the hypotenuse of an isoscels triangle is 3√2 cm, the area is _______

Solution: 4\(\frac{1}{2}\)

Example 2. When each side of an equilateral triangle is increased by 10%, its altitude increased by ________%.

Solution: 10%.

Example 3. When each side of an equilateral triangle is increased by 10%, its area increased by _________%.

Solution: 19%.

Example 4. The length of a median of an equilateral triangle of area 4√3 sq cm is ________ cm

Solution: 2√3

Example 5. In an isosceles right-angled triangle, the length of hypotenuse is √2 cm then the length of each equal sides is _______ cm.

Solution: 1.

Example 6. The length of two sides holding the right angle in a right-angled triangle are 3 cm and 4 cm. The length of the perpendicular drawn from the right angle to the hypotenuse is _______ cm.

Solution: 2 \(\frac{2}{5}\)cm.

Example 7. If each side of a square is increased by 10%, then the area is increased by ________ %.

Solution: 21%.

Example 8. The perimeter of a square is m metre. It is area is _______ sq m.

Solution: \(\frac{m^2}{16}\)

Example 9. The area of a square is 8k metre, the length of its diagonal is ________ m.

Solution: 4√k

Example 10. The perimeter of the square whose area is equal to sum of the areas of two square of sides 8 metre and 6 metre respectively is _______ metre.

Solution: 40.

Mensuration Chapter 1 Area And Perimeter Of Triangle And Quadrilateral Useful Information And Formulae True Or False

Example 1. The two diagonals of a rhombus are 24 m, 10 m. It is area is 120 sq cm.

Solution: The statement is True.

Example 2. If the three sides of an equilateral triangle be (x + 3) cm, (y + 4) cm, (x + y) cm, then the triangle with the sides (2xy + 1) cm, (6x + 1) cm and (8y+ 1) cm is also an equilateral triangle.

Solution: The statement is True.

Example 3. The length of a rectangle is 3 cm longer than its breadth. If its breadth be x cm, then the area is (x² + x) sq cm.

Solution: The statement is False.

Example 4. The length of a rectangle is 3 times that of its breadth. If the perimeter of the rectangle is 32 cm, its area is 4.8 sq cm.

Solution: The statement is False.

Example 5. The area of an equilateral triangle is 9√3 sq cm. The length of the median is 3√3 cm.

Solution: The statement is True.

Example 6. The centriod of an equilateral triangle ΔABC is G. If AB = 6 m, then AG = 2√3 cm.

Solution: The statement is True.

Example 7. The measure of each side of two equal sides of an isosceles triangle is 10 cm and measure of its base is 16 cm. The area is 16 sq cm.

Solution: The statement is False.

Example 8. A square and an equilateral triangle stand on same base. Area of the triangle = √3/2 x area of the square.

Solution: The statement is False.

Example 9. If number of metres of the perimeter of an equilateral triangle is equal to the number of sq metres of the area of the triangle. Measure of each side of the triangle is 4√3 metres.

Solution: The statement is True.

Example 10. D, E, and F are the midpoints of the sides BC, CA, and AB of a triangle ABC respectively. If the area of the triangle ABC = 24 sq em then ΔDEF = 6 sq cm.

Solution: The statement is True.

Mensuration Chapter 1 Area And Perimeter Of Triangle And Quadrilateral Useful Information And Formulae Short Answer Type Questions

Example 1. If the length of a square increased by 10%, then what % of the area will be increased?

Solution: Let length of the side be a unit.

∴ Area = a² sq units

increased side = \(\frac{11a}{10}\) unit

increased area = \(\frac{121 a^2}{1 a}\)

area % increased = \(=\frac{\frac{121 a^2}{1 a}-a^2}{a^2} \times 100=21\)

∴ 21% of the area will be increased.

Example 2. If the length is increased by 10% and breadth is decreased by 10% of a rectangle, then what % of area will be increased or decreased?

Solution: Let length and breadth be a and b units area = ab sq units.

Increased length = \(\frac{11a}{10}\) unit

decreased breadth = \(\frac{9a}{10}\)

New area = \(\frac{99 a^2}{100}\) sq units.

area % decreased = \(\frac{\frac{a^2-99 a^2}{100}}{a^2} \times 100=1\)

∴ 1% of area will be decreased.

Example 3. The length of rectangle is 5 cm. The length of the perpendicular on a breadth of the rectangle from an intersecting point between two diagonals is 2 cm. What is the length and breadth?

Solution: OP = 5 cm.

BC = 2 x 2 cm = 4 cm (from mid point theorem)

Let DC = x cm

∴ 4² + x² = 5²

x = 3

∴ The length and breadth 3 cm.

Example 4. The perimeter of a rectangle is 34 cm and area is 60 sq cm. Find the length of each diagonal.

Solution: If length and breadth are x cm, y cm then 2 (x + y) = 34

or, x + y = 17

xy = 60

(x + y)² = 17²

or, x² + y² = 17² – 2 x 60

= 289 – 120 = 169

∴ \(\sqrt{x^2+y^2}\) = 13

∴ Length of each diagonal = 13 cm.

Example 5. The numerical values of area and height of an equilateral triangle are cuqal. Find the length of each side.

Solution: \(\frac{\sqrt{3}}{4}\) x (side)²

= \(\frac{\sqrt{3}}{2}\) x (side)

∴ The length of each side = 2 units.

Example 6. The length of each side of an equilateral triangle is doubled. What % of area will be increased?

Solution: Let each side be a unit, area = \(\frac{\sqrt{3}}{4}\) a² sq unit

New area = \(\frac{\sqrt{3}}{4}\) (2a)² sq. unit = √3a²

% area increased = \(=\frac{\sqrt{3} a^2-\frac{\sqrt{3}}{4} a^2}{\frac{\sqrt{3}}{4} a^2} \times 100=\frac{3 \sqrt{3}}{4} 4^2 \times \frac{4}{\sqrt{3} q^2} \times 1 a=300\)

∴ 300% of area will be increase.

Example 7. The length of sides of a right-angled triangle are (x – 2) cm, x cm and (x + 2) cm. Find the hypotenuse?

Solution: (x + 2)² = x² + (x – 2)²

or, (x + 2)² – (x – 2)² = x²

or, 4.x.2 = x² or, x = 8

∴ Length of the hypotenuse 10 cm.

Example 8. A square drawn on height of equilateral triangle. Find ratio of areas of triangle and square.

Solution: Let length of each side of the equilateral triangle be x cm

∴ height = \(\frac{\sqrt{3}}{2}\)x cm

Required ratio = \(\frac{\sqrt{3}}{4} \dot{x}^2:\left(\frac{\sqrt{3}}{2} x\right)^2\)

= \(\frac{\sqrt{3}}{4} x^2: \frac{3 x^2}{4}=1: \sqrt{3}\)

∴ Ratio of areas of triangle and square = 1: √3.

Example 9. In parallelogram ABCD, AB = 4 cm, BC 6 cm, ∠ABC 30°, find the area.

Solution: We draw ⊥ from A to BC which intersects AC at P.

Extend AP to Q such that AP = PQ

From ΔAPB and ΔQPB,

AP = QP, ∠APB = ∠QPB (= 90°)

BP in common.

∴ ΔAPB = ΔQΡΒ

∴ ∠ABP = ∠QBP = 30°

∠ABQ = 30° + 30° = 60°

∠BAP = 180° – ∠APB – ∠ABP

= 180° – 90° – 30° = 60°

∴ ∠BQP = ∠BAP 60°

In ΔABQ, ∠ABQ = ∠BAQ = ∠BQA = 60°

∴ ΔABQ is equilateral of side equal to 4 cm.

AP = \(\frac{1}{2}\) = AQ = 2 cm  (AP = QP)

Required area = BC x AP = 6 x 2 sq cm = 12 sq cm.

Example 10. Length of height of a rhombus is 14 cm and length of side is 5 cm. Find the area.

Solution: Area = base x height

= 14 x 5 sq cm = 70 cm.

∴ Area of the rhombus is 70 cm.