Haritha

Geometry Chapter 4 Theorems On Concurrence

⇔ Concurrent lines: If two or more different straight lines having a common point is said to be concurrent lines.

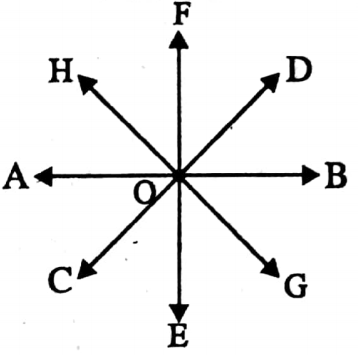
⇒ AB, CD, EF and GH are concurrent lines.

⇔ Circumcentre of a triangle: The point where the three perpendicular bisectors of sides of a triangle intersect is called the circumcentre of the triangle.

⇒ In ΔABC, the three perpendicular bisectors of AB, BC and CA meet at the point O; the point O is called the circumcentre and OA or OB or OC is the circumradius of ΔABC.

Read and Learn More  WBBSE Solutions For Class 9 Maths

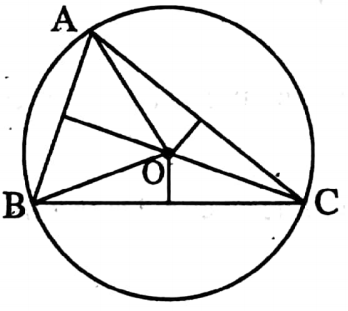
⇒ [OA = OB = OC]

⇒ A circle is drawn passing through the points A, B and C is called circum circle.

⇔ Incentre of a triangle: The point where the three internal bisectors of angles of a triangle intersect is called the incentre of the triangle.

In ΔABC, the internal bisectors of angles ∠A, ∠B and ∠C intersect each other at the point O.

I drawn OD ⊥ BC;

A circle is drawn with centre O and length of equal radius of OD is said to be in circle of ΔABC.

The circle touch AC and AB at E and F respectively. Centre of the circle is called incentre.

⇔ Centroid of a triangle: The point where the three medians of a triangle intersect is said to be centroid of a triangle.

⇒ Three medians AD, BE and CF of a triangle ABC, intersect at the point G.

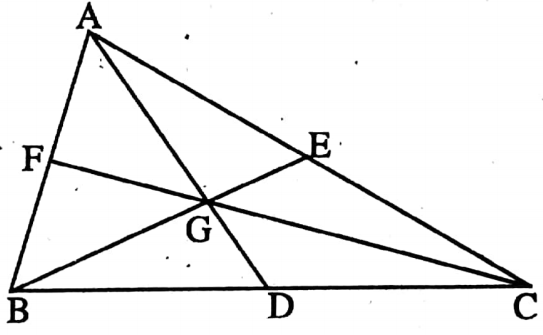
⇒ The point G is called the centroid of the ΔABC.

⇒ The centroid divides any median from the vertex in the ratio 2: 1.

⇔ Orthocentre of a triangle: The point where perpendiculars on the opposite sides from the three vertices of any triangle is called the orthocentre of the triangle.

⇒ In ΔABC, AD ⊥ BC, BE ⊥ CA and CF ⊥ AB;

⇒ AD, BE and CF meets at point O.

⇒ The point O is the orthocentre of ΔABC.

⇒ The triangle DEF obtained by joining the three points D, E, and F of ΔABC, is called a pedal triangle.

⇔ External centre: The point where the external bisectors of two angles and one internal bisector of an angle of a triangle intersect is called external centre.

⇒ In ΔABC, external bisectors of ∠ABC and ∠ACB and internal bisector of ∠BAC intersect at point O.

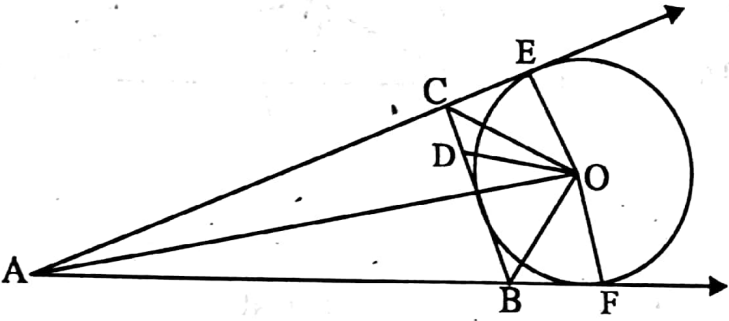
So O is the external centre.

OD, OE, OF are said to be external radius and the circle passes through the points D, E and F are called external circles of the triangle ABC.

Theorems:

1. The perpendicular bisectors of sides of triangle are concurrent.
2. The perpendiculars from vertices of triangle on the opposite sides are concurrent.
3. The internal bisectors of angles of triangle are concurrent.
4. The three medians of a triangle are concurrent.

Geometry Chapter 4 Theorems On Concurrence True Or False

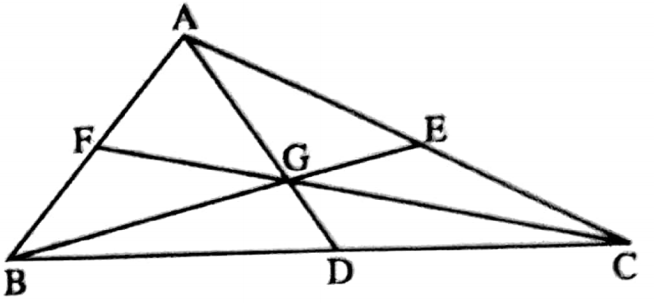
Example 1. The sum of lengths of three medians of a triangle is greater than three-fourth of its perimeter.

Solution: In ΔABC, the medians AD, BE and CF intersects at G (centroid).

∴ \(\frac{A G}{G D}=\frac{2}{1}\)

[centroid of a triangle divides any median from the vertex in the ratio 2: 1]

⇒ \(\frac{G D}{A G}=\frac{1}{2}\)

⇒ \(\frac{G D}{A G}+1=\frac{1}{2}+1\)

⇒ \(\frac{G D+A G}{A G}=\frac{3}{2}\)

⇒ \(\text { i.e. } \frac{A D}{A G}=\frac{3}{2}\)

⇒ \(A G=\frac{2}{3} A D\)

Similarly, BG = \(\frac{2}{3}\)  BD and CG = \(\frac{2}{3}\) CF

In ΔABG, AG + BG > AB…….(1)

In ΔBCG, BG + CG > BC……..(2)

In, ΔACG, CG + AG > AC……….(3)

[The sum of lengths of two sides of a triangle is greater than the length of third side]

(1) + (2) + (3) we get

2(AG + BG + CG) > AB + BC + AC

2(\(\frac{2}{3}\) AD + \(\frac{2}{3}\) BE + \(\frac{2}{3}\) CF) > AB + BC + CA

⇒ \(\frac{4}{3}\)(AD + BE + CF) > AB + BC + CA

⇒ AD + BE + CF > \(\frac{3}{4}\) (AB + BC + CA)

So the statement is true.

Example 2. The orthocentre of a triangle is a point equidistance from its three sides.

Solution: In the adjoining figure, if O is the incentre of the triangle ABC, then OD = OE = OF [Inradius]

i.e. the point equidistance from three side of a triangle is incentre.

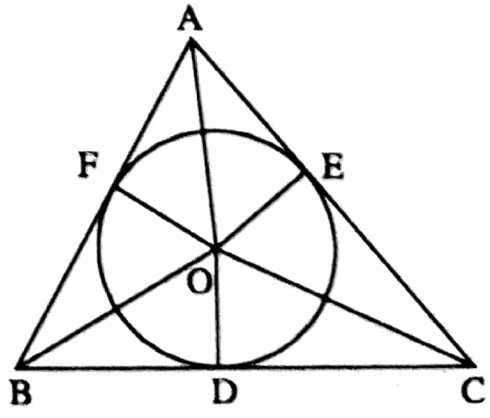
So the statement is false.

Example 3. In ΔABC, the internal bisectors ∠B and ∠C are meets at point O; if ∠BOC = 112°, then the value of ∠BAC is 44°.

Solution: In ΔABC, OB and OC are bisectors of ∠B and ∠C.

∴ ∠OBC = \(\frac{1}{2}\) ∠ABC and ∠OCB = \(\frac{1}{2}\) ∠ACB

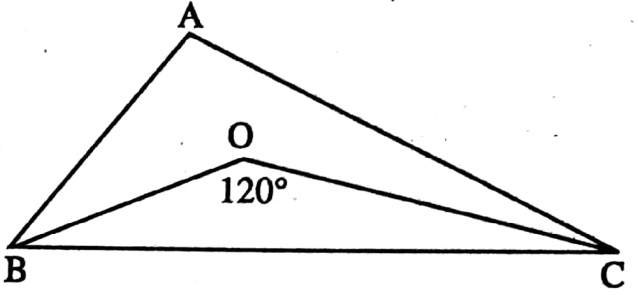
∠OBC + ∠OCB = \(\frac{1}{2}\) (∠ABC + ∠ACB)

⇒ 180° – ∠BOC = \(\frac{1}{2}\) (180° – ∠BAC)

⇒ 180° – ∠BOC = 90° – \(\frac{1}{2}\) ∠BAC

⇒ 180° – 112° = 90° – \(\frac{1}{2}\) ∠BAC

⇒ 68° = 90° – \(\frac{1}{2}\) ∠BAC

⇒ \(\frac{1}{2}\) ∠BAC = 90° – 68° = 22°

⇒ BAC = 44°

∴ The statement is true.

Geometry Chapter 4 Theorems On Concurrence Fill In The Blanks

Example 1. The length of circumradius of a right-angled triangle is ________ of hypotenuse.

Solution: Half

[OA = OB = OC]

Example 2. The two medians of triangle are together than the third median.

Solution: Greater.

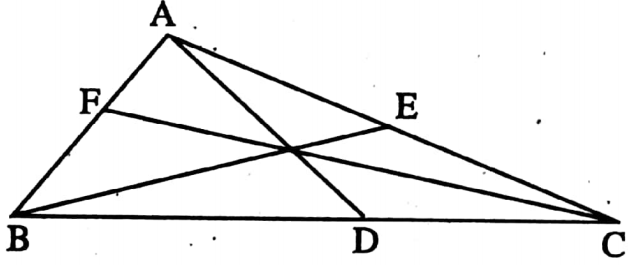
Example 3. If in ΔABC, three medians AD, BE and CF meets at point G then area of ΔABC area of ΔAGE is __________

Solution: ΔAGE = \(\frac{1}{6}\) ΔABC

⇒ \(\frac{\triangle \mathrm{ABC}}{\triangle \mathrm{AGE}}=\frac{6}{1}\)

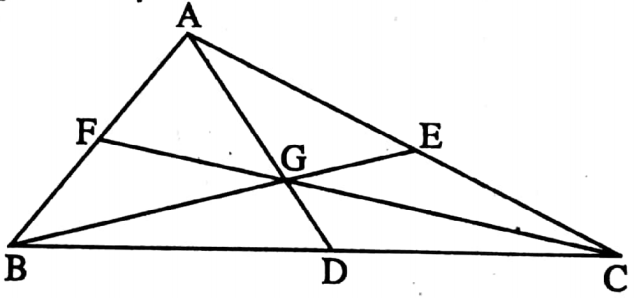
⇒ ΔABC: ΔAGE = 6 : 1

Geometry Chapter 4 Theorems On Concurrence Short Answer Type Questions

Example 1. If the lengths of sides of triangle are 6 cm, 8 cm and 10 cm, then write where the circumcentre of this triangle lies.

Solution: 6²+ 8² = 100 = 10²

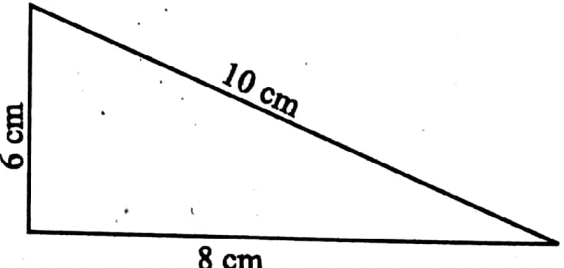
⇒ So the triangle is a right-angled triangle.

⇒ So the circumcentre of the triangle lies on the midpoint of hypotenuse i.e. lies on the midpoint of side with 10 cm in length.

Example 2. AD is the median and G is the centroid of an equilateral triangle. If the length of side 3√3 cm, then find the length of AG.

Solution: The medians and heights of any equilateral triangle are equal in length.

∴ The length of median AD.

= \(\frac{\sqrt{3}}{2}\) x length of side

= \(\left(\frac{\sqrt{3}}{2} \times 3 \sqrt{3}\right) \mathrm{cm}\)

= \(\frac{9}{2} \mathrm{~cm}=4.5 \mathrm{~cm}\)

centroid of a triangle divides any median from the vertex in the ratio 2: 1

∴ \(\frac{AB}{GD}\) = \(\frac{1}{2}\)

let AG = 2x cm

and GD x cm [x is common multiple and x > 0]

AG + GD = (2x + x) cm = 3x cm

3x = 4.5

⇒ x = 1.5

∴ AG = (2 x 1.5) cm = 3 cm.

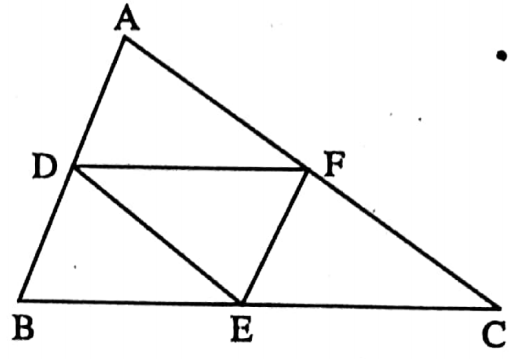
Example 3. DEF is a pedal triangle of an equilateral triangle ABC. Find the value of ∠FDA.

Solution: In ΔABD and ΔACD,

∠ADB = ∠ADC = 90°  [AD ⊥ BC]

⇒ hypotenuse AB = hypotenuse AC  [ΔABC is an equilateral]

⇒ and AD = AD [common side]

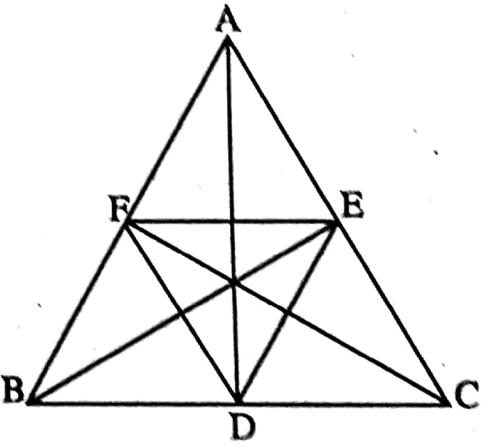
∴ ΔABD ≅ ΔACD [by R-H-S criterion of congruency]

∴ BD = CD i.e. D is the mid point of BC

and ∠BAD = ∠CAD = \(\frac{60^{\circ}}{2}\) = 30°

Similarly, F and E are the mid points of AB and AC respectively.

∴ FE || BC and FE = \(\frac{1}{2}\) BC

⇒ Similarly, DE = \(\frac{1}{2}\) AB and FD = \(\frac{1}{2}\) AC

As AB = BC = CA

∴ DE = FE = FD

∴ ΔDEF is an equilateral triangle.

∴ ∠ZDFE = 60°

⇒ As FE || BC and AB is intersection

∴ ∠AFE corresponding ∠ABC = 60°

∴ ∠AFD = ∠AFE + ∠DEF

= 60° + 60° = 120°

In ΔAFD, ∠FDA + ∠AFD + ∠FAD = 180°

∠FDA + 120° + 30 ° = 180°

⇒ ∠FDA = 30°

Example 4. ABC is an isosceles triangle in which ∠ABC = ∠ACB and median AD = \(\frac{1}{2}\) BC. If AB = √2 cm, then find the length of the circumradius of this triangle.

Solution: In ΔABC, ∠ABC = ∠ACB

∴ AC = AB

⇒ In ΔABD and ΔACD,

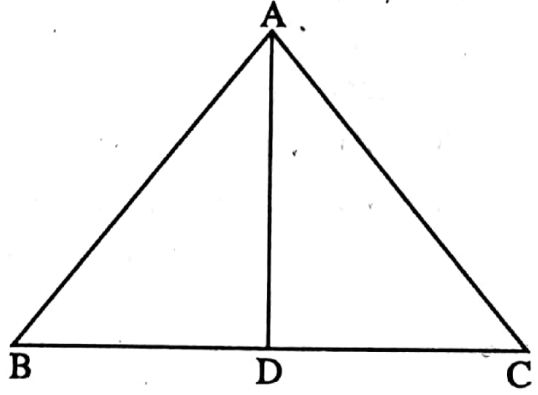
⇒ AB = AC, AD = AD  [common side]

⇒ and BD = CD  [D is the mid point of BC]

∴ ΔABD ≅ ΔACD [By S-S-S criterion of congruency]

∴ ∠ADB = ∠ADC

∠ADB + ∠ADC = 180°

∴ ∠ADB + ∠ADB = 180°

⇒ 2 ∠ADB = 180°

⇒ ∠ADB = 90°

∴∠ADC = 90°

⇒ Again, AD = \(\frac{1}{2}\) BC = BD = CD

∴ BD or CD or AD is the circumradius of ΔABC.

⇒ In right-angled triangle ABD, ∠ADB = 90°

∴ AD²+ BD² = AB² [By Pythagorus theorem]

BD² + BD² = (√2)² cm²

⇒ 2BD² = 2 cm²

⇒ BD² = 1 cm²

⇒ BD = √1 cm = 1 cm

⇒ The length of circumradius of ΔABC is 1 cm.

Example 5. In ΔABC, two medians AD and BE are perpendicular each other at point G. If BC = 8 cm and AC = 6 cm, then find the length of AB.

Solution: In ΔABC, the medians AD and BE intersects at G.

⇒ So G is the centroid of the ΔABC.

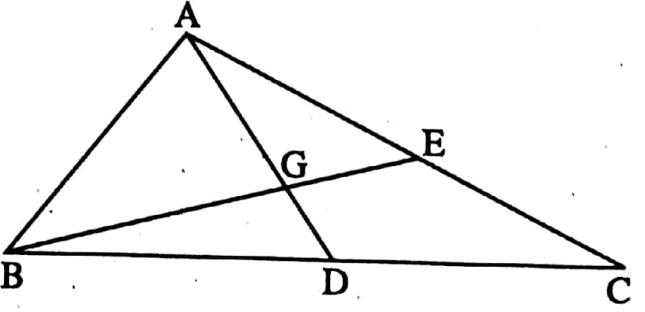
⇒ ∠AGB = ∠AGE = ∠DGB = 90° [AD ⊥ BE]

⇒ AG: GD = 2 : 1 and BG: GE = 2:1

⇒ Let, AG = 2x cm and GD = x cm

⇒ BG= 2y cm and GE = y cm

⇒ BG = 2y cm and GE = y cm [x and y are common multiples and x > 0, y > 0]

∴ BD = \(\frac{1}{2}\) BC = (\(\frac{1}{2}\) x 8) cm = 4 cm and AE = \(\frac{1}{2}\) AC = (\(\frac{1}{2}\) x 6) cm = 3 cm

⇒ In ΔAGE, ∠AGE = 90°

∴ AG² + GE² = AE² [By Pythagorus theorem]

⇒ (2x)² + (y)² = (3)²

⇒ 4x² + y² = 9………(1)

⇒ In ΔBGD, ∠BGD = 90°

∴ BG² + GD² = BD²

⇒ (2y)² + x² = 4²

⇒ 4y² + x² = 16 …….(2)

⇒ (1) + (2), we get,

⇒ 4x² + y² + 4y² + x² = 9 + 16

⇒ 5x² + 5y² = 25  ⇒ x² + y² = 5

⇒ In ΔABG, ∠AGB = 90°

∴ AB² = AG² + BG²

= ((2x)² + (2y)²) cm²

= 4(x² + y²) cm²

= 4 x 5 cm² = 20 cm²

⇒ AB = √20 cm

= √4×5 cm = 2√5 cm

⇒ The length of AB is 2√5 cm.

Example 6. O is the circumcentre of triangle ABC. If ∠OBC = 30° then find the value of ∠BAC.

Solution: I join A, O and AO is extended at P.

⇒ In ΔBOC, OB = OC [circumradius]

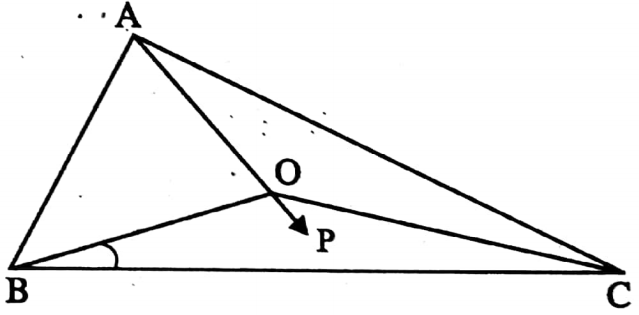
∴ ∠OCB = ∠OBC = 30°

⇒ ∠BOC = 180° (30° + 30°) = 120°

⇒ In ΔAOB, OA = OB

∴ ∠OAB = ∠OAB

The exterior ∠BOP = ∠OAB + ∠OBA

= ∠OAB + ∠OAB = 2 ∠OAB

Similarly, ∠COP = 2 ∠OAC

∠BAC = ∠OAB + ∠OAC

= \(\frac{1}{2}\)(∠BOP + ∠COP)

= \(\frac{1}{2}\) ∠BOC = \(\frac{1}{2}\) x 120° = 60°

Example 7. If the point O is the orthocentre of ΔABC then find the relation between ∠BOC and ∠BAC.

Solution: In ΔABC,

⇒ AD ⊥ BC, BE ⊥ AC and CF ⊥ AB.

⇒ AD, BE and CF intersects at point O.

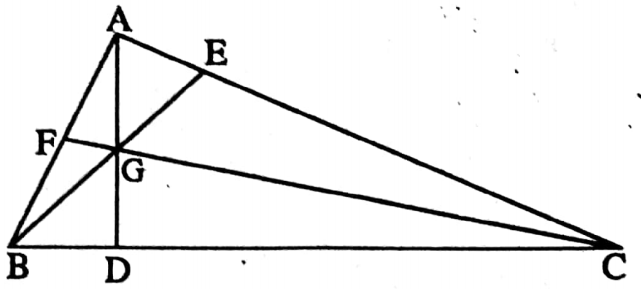
∴ ∠AEB = ∠AFC = 90°

⇒ In quadrilateral AEOF,

⇒ ∠EAF + ∠AFO + ∠EOF + ∠AEO = 360°

⇒ ∠EAF + 90° + ∠EOF + 90° = 360°

⇒ ∠EAF + ∠BOC = 360° – 180°  [∠EOF = vertically opposite ∠BOC]

⇒ i.e. ∠BAC + ∠BOC = 180° [required relation]

Example 8. In ΔABC, D, E and F are midpoints of side, BC, CA and AB respectively. If AB = 5 cm, BC = 6 cm and CA = 7 cm, then find the perimeter of ΔDEF.

Solution: In ΔABC, F and E are midpoints of side AB and AC respectively,

∴ FE = \(\frac{1}{2}\) BC = (\(\frac{1}{2}\) x 6) cm = 3 cm

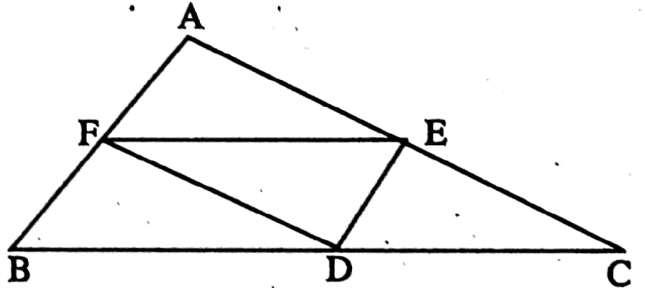
⇒ Similarly, DE = \(\frac{1}{2}\) = AB = (\(\frac{1}{2}\) x 5) cm = 2.5 cm

⇒ and FD = \(\frac{1}{2}\) AC = (\(\frac{1}{2}\) x 7) cm = 3.5 cm

∴ Perimeter of ΔDEF = (3 + 2.5+ 3.5) cm = 9 cm.

Geometry Chapter 3 Theorems On Area

Theorem:

1. The area of parallelograms which stand on same base and between same parallels are equal.
2. When a triangle and any parallelogram are on the same base and between the same parallels, the area of a triangle is half the area of the parallelogram.
3. The area of triangular regions being on the same base and between same parallels is equal.
4. Triangular regions of equal area standing on same base and being on the same side of it, they will be between the same parallels.

Geometry Chapter 3 Theorems On Area True Or False

Example 1. The heights of each parallelogram between the same parallel lines are same.

Solution: The perpendicular distance between two parallel lines are same.

⇒ The parallelogram ABCD and parallelogram PQRS are between the same parallels.

⇒ Therefore, the statement is True.

Example 2. The area of parallelogram ABCD is 32 sq. cm. O is any point on diagonal BD. If the area of ΔAOD is 5 sq. cm then the area of ΔAOP is 4 sq. cm.

Solution: I join A, C.

⇒ The diagonal AC intersects BD at point P;

⇒ So AC and BD bisects each other at point P.

ΔADC = \(\frac{1}{2}\) parallelogram ABCD

= (\(\frac{1}{2}\) x 32) sq. cm = 16 sq. cm

⇒ DP is a median of ΔADC

∴ ΔADP = \(\frac{1}{2}\) ΔADC

= (\(\frac{1}{2}\) x 16) sq. cm = 8 sq. cm

⇒ ΔAOD = 5 sq. cm

⇒ ΔΑΟΡ = ΔADP – ΔAOD

= (8 – 5) sq. cm = 3 sq. cm

⇒ So the statement is false.

Geometry Chapter 3 Theorems On Area Fill In The Blanks

Example 1. The _______ of a triangle divides the triangular region into two equal parts of triangular regions.

Solution: median.

⇒ [ΔABD = ΔACD]

Example 2. If a triangle and a parallelogram are on the same base and between the same parallels, the ratio of areas between a parallelogram and a triangle is _______

Solution: 2 1.

⇒ ΔABC and parallelogram BCDE are on same base BC and between the same parallels.

∴ ΔABC = parallelogram BCDE

⇒ or, \(\frac{\text { parallelogram } \mathrm{BCDE}}{\triangle \mathrm{ABC}}=\frac{2}{1}\)

as, parallelogram BCDE: ΔABC= 2:1

Example 3. ΔABC and rhombus BCDE are on the same base and between the same parallels BC and FD. If ΔABC = 18 sq. cm and BC = 8 em then height of rhombus BCDE is _______

Solution: 4.5 cm.

⇒ Area of rhombus BCDE = 2 ΔABC = (2 x 18) sq.cm = 36 sq. cm

⇒ BC = 8 cm

∴ Height = \(\frac{36}{8}\) 36 cm = 4.5 cm.

Geometry Chapter 3 Theorems On Area Short Answer Type Questions

Example 1. DE is perpendicular on side AB from point D of parallelogram ABCD and BF is perpendicular on side AD from the point B ; If AB = 10 cm, AD = 8 cm, and DE 6 cm; Find the length of BF.

Solution: Area of parallelogram = base x height DE = AD × BF

⇒ Area of parallelogram ABCD = AB x DE = AD x BF

⇒ 10 cm = 6 cm = 8 cm x BF

⇒ or, BF = \(\frac{60}{8}\) cm = \(\frac{15}{2}\) = 7.5 cm

∴ The length of BF is 7.5 cm.

Example 2. The area of the parallelogram-shaped region ABCD is 100 sq. units. P is the midpoint of side BC; Find the area of triangular region ABP.

Solution: I join A and C.

⇒ AC is a diagonal of parallelogram ABCD.

∴ ΔABC = \(\frac{1}{2}\) parallelogram ABCD

= (\(\frac{1}{2}\) x 100)sq. unit = 50 sq. unit

AP is a median of ΔABC

∴ΔABP = \(\frac{1}{2}\) ΔABC = (\(\frac{1}{2}\) x 50) sq. unit

= 25 sq. unit.

∴ The area of the triangular region of ΔABP is 25 sq. unit.

Example 3. AD is the median of triangle ABC and P is any point on side AC in such a way that area of ΔADP: area of ΔABD = 2: 3. Find the area of ΔPDC: area of ΔABC.

Solution: AD is a median of ΔABC

∴ ΔABD = ΔADC = \(\frac{1}{2}\) ABC

\(\frac{\triangle \mathrm{ADP}}{\triangle \mathrm{ABD}}=\frac{2}{3}\) [given]

∴ \(\frac{\Delta \mathrm{ADP}}{\Delta \mathrm{ADC}}=\frac{2}{3}\)

[ΔABD = ΔADC]

⇒ or, \(\triangle \mathrm{ADP}=\frac{2}{3} \triangle \mathrm{ADC}\)

⇒ as, \(\frac{\Delta \mathrm{PDC}}{\Delta \mathrm{ABC}}=\frac{\Delta \mathrm{ADC}-\Delta \mathrm{ADP}}{\Delta \mathrm{ABC}}\)

= \(\frac{\Delta \mathrm{ADC}-\frac{2}{3} \Delta \mathrm{ADC}}{\Delta \mathrm{ABC}}=\frac{\frac{1}{3} \Delta \mathrm{ADC}}{\Delta \mathrm{ABC}}\)

= \(\frac{\frac{1}{3} \times \frac{1}{2} \Delta \mathrm{ABC}}{\Delta \mathrm{ABC}}=\frac{1}{6}\)

∴ ΔPDC: ΔABC = 1: 6.

Example 4. BDE is a parallelogram. F is midpoint of side ED. If area of triangular region ABD is 20 sq. unit, then find the area of triangular region AEF.

Solution: AD is a diagonal of parallelogram ABDE

⇒ ΔADE = ΔABD = 20 sq. cm

⇒ AE is an median of ΔADE

∴ ΔAEF = \(\frac{1}{2}\) ΔADE

= (\(\frac{1}{2}\) x 20) sq cm = 10 sq. cm

∴ The area of triangular is 10 sq. cm.

Example 5. PQRS is a parallelogram. X and Y are the midpoints of side PQ and SR respectively. Join diagonal SQ, Find the area of the parallelogram shaped region XQRY: area of triangular region QSR.

Solution: I join Q, Y.

⇒ In quadrilateral XQRY,

⇒ QX || RY  [PQ || SR]

and QX = RY  [\(\frac{1}{2}\) PQ = \(\frac{1}{2}\) SR]

∴ XQRY is a parallelogram.

⇒ QY is a diagonal of parallelogram XQRY.

∴ ΔQRY = \(\frac{1}{2}\) parallelogram XQRY

⇒ or, Parallelogram XQRY = 2 ΔQRY……..(1)

⇒ QY is a median of ΔQSR.

∴ ΔQRY = \(\frac{1}{2}\) ΔQSR

⇒ or, ΔQSR = 2 ΔQSR

⇒ or, ΔQSR = 2 ΔQRY……(2)

⇒ From (1) and (2), parallelogram XQRY = ΔQSR

∴ Parallelogram XQRY: ΔQSR = 1: 1.

Example 6. If the area of parallelogram PQRS is 15 sq. cm, then find the area of parallelogram PMNO.

Solution: I join O, Q.

⇒ ΔPOQ and parallelogram PQRS are on same base and between the same parallels.

∴ ΔPOQ = \(\frac{1}{2}\) parallelogram PQRS

= (\(\frac{1}{2}\)x 15) sq. cm

= 7.5 sq. cm

⇒ Similarly, ΔPOQ = \(\frac{1}{2}\) = parallelogram PMNO

⇒ or, parallelogram PMNO = 2 ΔPOQ

= (2 x 7.5) sq. cm = 15 sq. cm

∴ The area of parallelogram PMNO is 15 sq. cm.

Example 7. In ΔABC D is the midpoint of side AB and DBCE is a parallelogram; If the area of ΔABC is 40 sq. cm, then find the area of parallelogram DBCE.

Solution: DE intersects AC at point F.

⇒ In ΔABC, D is the midpoint of AB and DE || BC;

∴ F is the midpoint of AC.

In ΔADF and ΔCEF,

∠AFD = ∠CFE [vertically opposite angles]

∠DAF = alternate ∠ECF

[AB || CE and AC is intersection]

∴ AF = CF

∴ ΔADF ≅ ΔCEF [By A-A-S criterion of B congruences]

∴ ΔADF = ΔCEF

Area of parallelogram DBCE

= Area of ΔCEF + area of quadrilateral ΔCFD

= Area of ΔADF+ area of quadrilateral BCFD = Area of ΔABC= 40 sq. cm.

∴ The area of parallelogram DBCE is 40 sq. cm.

Example 8. In trapezium, ABCD, AD || BC, and P and Q are midpoints of side AB and DC 18 em then find the ratio of area of quadrilateral APQD respectively. If AD = 12 cm and BC and area of quadrilateral PBCQ.

Solution: P and Q are the midpoints of side AB and DC respectively.

∴ PQ || AD || BC

and PQ = \(\frac{1}{2}\) (AD + BC) = \(\frac{1}{2}\) (12 + 18) cm = 12 cm

AS, AD || PQ  ∴ APQD is a trapezium

Similarly, PBCQ is a trapezium

As P and Q are midpoints of side AB and DC respectively

∴ Height of trapezium APQD and PBCQ are same.

Let, this height be h cm.

∴ Area of trapezium APQD = \(\frac{1}{2}\) (AD + PQ) x h

= \(\frac{1}{2}\) (12 + 15) x h sq. cm = \(\frac{27h}{2}\) sq. cm.

Area of trapezium PBCQ = \(\frac{1}{2}\) (PQ + BC) x h

= \(\frac{1}{2}\) (15 + 18) x h sq. cm. = \(\frac{33h}{2}\) sq. cm

∴ Ratio of areas between two trapezium is \(\frac{27h}{2}\): \(\frac{33h}{2}\)

= \(\frac{27h}{2}\): \(\frac{33h}{2}\) = 9: 11

∴ The ratio of area of quadrilateral APQD and area of quadrilateral PBCQ is 9: 11.

Example 9. In ΔABC, D and E are midpoints of side AB and BC respectively; F is the midpoint of side AD. If the area of ΔABC is 24 sq. cm then find the area of ΔCEF.

Solution: I join C, D. CD is a median of ΔABC

∴ ΔADC = \(\frac{1}{2}\) ΔABC

Again, CF is a median of ΔADC

∴ ΔACF = \(\frac{1}{2}\) ΔADC

= \(\frac{1}{2}\) x \(\frac{1}{2}\) ΔABC = \(\frac{1}{2}\) ΔABC

FE is a median of ΔFBC

∴ ΔCEF = \(\frac{1}{4}\) ΔFBC

= \(\frac{1}{2}\) (ΔABC – ΔACF)

= \(\frac{1}{2}\) (ΔABC – \(\frac{1}{4}\) ΔABC)

= \(\frac{1}{2}\) x \(\frac{3}{4}\) ΔABC

= (\(\frac{3}{8}\) x 24) sq. cm = 9 sq. cm

∴ The area of ACEF is 9 sq. cm.

Example 10. In parallelogram ABCD, the points P and Q on sides AB and DC such that BP = 2AP and DQ = 2CQ; If the area of parallelogram ABCD is 36 sq. cm then find the area of quadrilateral APCQ.

Solution: BP = 2AP

as, AB – AP = 2AP

or, AB = 3AP

or, AP = \(\frac{1}{3}\) AB

Similarly, CQ = \(\frac{1}{3}\) DC

Again AB = DC

∴ 3AP = 3CQ

or, AP = CQ

In quadrilateral APCQ, AP = CQ and AP || CQ

∴ APCQ is a parallelogram

As parallelogram APCQ and parallelogram ABCD are between the same parallels AB and DC

∴ Their heights are same. Let height is h cm

∴ Area of parallelogram ABCQ = AP x h

= \(\frac{1}{3}\) AB x h = \(\frac{1}{3}\) x area of parallelogram ABCD

= (\(\frac{1}{3}\) x 36) sq. cm = 12 sq. cm

∴ The area of quadrilateral APCQ is 12 sq. cm.

Geometry Chapter 2 Transversal And Mid Point Theorem

Theorem:

1. The line segment joining the midpoints of two sides of a triangle is parallel to the third side and equal to half of it.
2. In any triangle, through the midpoint of any side, if a line segment is drawn parallel to the second side, then it will bisect the third side and the length of the line segment intersected by the two sides of the triangle is equal to the length of the half of the second side.
3. If three or more parallel straight lines make equal intercepts from a transversal, then they will make equal intercepts from another transversal.

[Proof of the Theorem (3) is not for evaluation]

Read and Learn More  WBBSE Solutions For Class 9 Maths

Geometry Chapter 2 Transversal And Mid Point Theorem True Or False

Example 1. In ΔABC, D, and E are the midpoints of AB and AC respectively. If the length of DE is 5 cm, then the length of BC is 10 cm.

Solution: In ΔABC, D and E are the midpoints of AB and AC respectively

∴ DE = \(\frac{1}{2}\) BC

⇒ BC = 2 DE (2 × 5) cm = 10 cm

⇒ So the statement is true.

Example 2. In the equilateral triangle ABC, D, E, and F are midpoints of side AB, BC, and CA respectively. If the perimeter of ΔDEF is 8 cm.

Solution: AB = BC = CA = \(\frac{12}{3}\) cm = 4 cm

⇒ D and F are midpoints of AB and AC.

∴ DF = \(\frac{1}{2}\) BC = (\(\frac{1}{2}\) x 4) cm = 2 cm

⇒ Similarly, EF = DE = 2 cm

∴ The perimeter of ΔDEF is (2 × 3) cm = 6 cm

∴ The statement is false.

Geometry Chapter 2 Transversal And Mid Point Theorem Fill In The Blanks

Example 1. If three or more _______ straight lines make equal intercepts from a transversal, then they will make equal intercepts from another transversal.

Solution: Parallel.

⇒ [If AB || CD || EF and MN = NO then GH = HI]

Example 2. The triangle formed by joining midpoints of consecutive sides of an equilateral triangle is a _______ triangle.

Solution: Equilateral.

Geometry Chapter 2 Transversal And Mid Point Theorem Short Answer Type Questions

Example 1. In the triangle, ABC, AD, and BE are two medians and DF is parallel to BE, meets AC at the point F. If the length of the side AC is 8 cm. Find the length of the side CF.

Solution: In ΔBCE, D is the midpoint of BC and DF || BE;

∴ F is the midpoint of EC,

∴ CF = \(\frac{1}{2}\) EC = \(\frac{1}{2}\) x \(\frac{1}{2}\) AC  [Midpoint of AC is E]

= \(\frac{1}{4}\) AC = (\(\frac{1}{4}\) x 8) cm

∴ CF = 2 cm.

∴ The length of the side CF is 2 cm.

Example 2. In the triangle, ABC, the midpoints of BC, CA, and AB are P, Q, and R respectively, if AC = 21 cm, BC = 29 cm, and AB = 30 cm perimeter of the quadrilateral ΔRPQ.

Solution: In ΔABC, P and Q are the midpoints of BC and AC respectively.

∴PQ = \(\frac{1}{2}\)AB = (\(\frac{1}{2}\)x 30)cm = 15 cm

⇒ Similarly, RP = \(\frac{1}{2}\) AC = \(\frac{1}{2}\)(21) cm = 10.5 cm

⇒ Again AR = \(\frac{1}{2}\) AB = (\(\frac{1}{2}\) x 30) cm = 15 cm

⇒ AQ = \(\frac{1}{2}\)AC = (\(\frac{1}{2}\) x 21)cm = 10.5 cm

∴ Perimeter of quadrilateral ARPQ is AR+ RP+ PQ+ AQ

= (15+ 10.5 + 15 + 10.5)cm = 51 cm

Example 3. In the triangle, ABC, D is any point on the side AC. The midpoints of AB, BC, AD, and DC are P, Q, X, and Y respectively. If PX = 5 cm, then write the length of the side QY.

Solution: XY = DX + DY

= \(\frac{1}{2}\) AD + \(\frac{1}{2}\) DC

= \(\frac{1}{2}\)(AD + DC)

= \(\frac{1}{2}\) AC

In ΔABC, P and Q are the midpoints of AB and BC

∴ PQ = \(\frac{1}{2}\) AC and PQ || AC

∴ XY = PQ and PQ || XY  [PQ || AC]

∴ PQYX is a parallelogram

∴ QY= PX = 5 cm.

∴ The length of the side QY is 5 cm.

Example 4. In the triangle ABC, the medians BE and CF intersects at the point G. The midpoints of BG and CG are P and Q respectively. If PQ = 3 cm, then find the length of BC.

Solution: In ΔGBC, the midpoints of BG and CG are P and Q respectively.

∴ PQ = \(\frac{1}{2}\) BC

⇒ BC = 2 PQ = (2 x 3) cm = 6 cm.

∴ The length of BC is 6 cm.

Example 5. In the triangle ABC, the midpoints of BC, CA, and AB are D, E, and F respectively, EF intersects AD at the point O. If AD = 6 em, then write the length of AO.

Solution: In ΔABC, F, and E are the midpoints of AB and AC respectively.

= FE || BC

⇒ In ΔABD, F is the midpoint of AB and FO || BD [FE || BC]

∴ O is the midpoint of AD

∴ AO = \(\frac{1}{2}\) AD = (\(\frac{1}{2}\) x 6) cm = 3 cm

∴ The length of AO is 3 cm.

Example 6. In the parallelogram ABCD, BC is extended to point P such that BC CP. Join A, P; AP is intersect CD and BD at the points Q and R respectively. If DR = 3 cm then find the length of BR.

Solution: Through point C a line segment parallel to BD is drawn which intersects AP at the point S.

⇒ In parallelogram ABCD, AD = BC

⇒ Again, BC = CP ∴ AD = CP.

⇒ In ΔADQ and ΔCPQ,

⇒ ∠AQD = ∠CQP [vertically opposite angles]

⇒ ∠DAQ alternate ∠CPQ [AD || BP and AP is intersection]

and AD = CP

∴ ΔADQ ≅ ΔCPQ  ∴ DQ = CQ

⇒ In ΔDQR and ΔCQS

⇒ ∠DQR = ∠CQS [vertically opposite angles]

⇒ ∠RDQ = alternate ∠SCQ and DQ = CQ

∴ ∠DQR ≅ ΔCQS,  ∴ DR = CS

⇒ In ΔBPR, C is the midpoint of BP and CS || BR

∴ CS = \(\frac{1}{2}\) BR

⇒ or, BR = 2 CS = 2 DR (2 x 3) cm = 6 cm.

∴ The length of BR is 6 cm.

Example 7. In the triangle, ABC, D, and E are the midpoints of AB and BC respectively. BC is extended to the point F such EC CF; Join D, F. If AC = 8 cm, then find the length of CG.

Solution: In ΔABC, D, and E are the midpoints of AB and BC respectively.

∴ DE || AC and DE = \(\frac{1}{2}\) AC

= (\(\frac{1}{2}\)x 8) cm = 4 cm

⇒ In ΔDEF, C is the mid point of EF and GC || DE [DE || AC]

⇒ In CG = \(\frac{1}{2}\) DE = (\(\frac{1}{2}\) x 4) cm = 2 cm.

‍ ∴ The length of CG is 2 cm.

Example 8. The area of a square is x² sq. cm. Find the perimeter of the quadrilateral formed by joining midpoints of consecutive sides of that square.

Solution: Let, P, Q, R and S are the midpoints of the sides AB, BC, CD, and DA respectively of a square ABCD.

I join P, Q; Q, R; R, S; S, P; A, C and B, D.

⇒ Area of the square ABCD is x² sq. cm.

∴ The length of each side is √x² cm or x cm and length of the each diagonal is √2x cm.

∴ AB = BC = CD = DA = x cm and AC = BD = √2x cm

⇒ In ΔABD, P and S are the midpoints of side AB and AD respectively.

⇒ PS || BD and PS = \(\frac{1}{2}\) BD \(\frac{\sqrt{2} x}{2}\) cm

∴ In the quadrilateral PQRS, PS || QR and PS = QR

∴ PQRS is a parallelogram.

⇒ In ΔABC, P and Q are the midpoints of AB and BC respectively

∴ PQ = \(\frac{1}{2}\) AC = \(\frac{\sqrt{2} x}{2}\) cm

∴ PQ = QR = \(\frac{\sqrt{2} x}{2}\) cm

⇒ In ΔBPQ, BP = BQ and ∠PBQ = 90°

∴ ∠BPQ = ∠BQP = \(\frac{180^{\circ}-90^{\circ}}{2}=45^{\circ}\)

⇒ Similarly, ∠APS = 45°

∴ ∠SPQ = 180° – ∠APS – ∠BPQ

= 180° – 45° – 45° = 90°.

⇒ Similarly, ∠PQR = 90°

⇒ As, in parallelogram PQRS, PQ = QR and ∠PQR = 90°

∴ PQRS is a square whose length of each sides is \(\frac{\sqrt{2} x}{2}\) cm

∴ Perimeter = (4 x \(\frac{\sqrt{2} x}{2}\)) cm = 2√2x cm.

∴ The perimeter of the quadrilateral form by joining midpoints of consecutive sides of that square is 2√2x cm.

Example 9. In the ΔABC, D, E, and F are midpoints of sides AB, BC, and CA respectively. In the ΔDEF, P, Q, and R are the midpoints of the sides DE, EF, and FD respectively. If PR = 3 cm then the length of AB.

Solution: In the ΔDEF, P and Q are midpoints of DE and DF respectively.

∴ PR = \(\frac{1}{2}\) EF

⇒ In the ΔABC, E and F are midpoints of BC and AC

∴ EF = \(\frac{1}{2}\) AB

⇒ or, AB = 2 EF = 2 x 2PR (4 x 3) cm = 12 cm.

∴ The length of AB is 12 cm.

Example 10. In the ΔABC, AB = x cm, BC = y cm, and ∠ABC = 90°. If D and E are midpoints of AB and BC, then find the perimeter of ΔBDE.

Solution: BD = \(\frac{1}{2}\) AB = \(\frac{x}{2}\) and BE = \(\frac{1}{2}\) BC = \(\frac{y}{2}\) cm

⇒ In ΔABC, ∠ABC = 90°

∴ AB² + BC² = AC² [By Pythagorus theorem]

⇒ AC = \(\sqrt{A B^2+B C^2}\)

= \(\sqrt{x^2+y^2} \mathrm{~cm}\)

⇒ In ΔABC, D, and E are the midpoints of AB and BC

∴ DE = \(\frac{1}{2}\) AC = \(\frac{\sqrt{x^2+y^2}}{2}\) cm

⇒ Perimeter of ΔBDE = BD + BE + DE

= \(\left(\frac{x}{2}+\frac{y}{2}+\frac{\sqrt{x^2+y^2}}{2}\right)\) cm

The perimeter of ΔBDE = \(\left(\frac{x}{2}+\frac{y}{2}+\frac{\sqrt{x^2+y^2}}{2}\right)\) cm

Algebra Chapter 2 Graph

⇒ The region within angle XOY is called 1st quadrant.

⇒ The region within angle YOX’ is called the 2nd quadrant.

⇒ The region within angle X’OY’ is called the 3rd quadrant and the region YOX is called the 4th quadrant.

⇒ We get the distance from Y-axis is X coordinate and the distance from X-axis is the Y coordinate.

⇒ O is called the origin. The X coordinate is called the abscissa and the Y-co-ordinate is called the ordinate.

⇒ The co-ordinate of origin O is (0, 0).

⇒ Signs of abscissa and ordinate in the different quadrants is shown.

Read and Learn More  WBBSE Solutions For Class 9 Maths

Algebra Chapter 2 Graph Fill In The Blanks

Example 1. Co-ordinate of origin is ______

Solution: (0, 0)

Example 2. Equation of X axis is ______

Solution: y = 0

Example 3. Equation of Y axis is ______

Solution: y = 0

Example 4. X + 8 = 0 is parallel to _______ axis.

Solution: Y axis

Example 5. (0, 8) point lies on ______ axis.

Solution: Y axis

Example 6. (-6, 0) lies on ______ axis.

Solution: X axis

Example 7. (-3, +5) lies in the ________ quadrant.

Solution: 2nd

Example 8. Distance of A (6, 8) from Y axis is ________ units.

Solution: 6

Example 9. 2x + 3y = 12 intersects X axis at ________

Solution: (6, 0)

Example 10. 2x + 3y 12 intersects Y axis at _________

Solution: (0, 4)

Algebra Chapter 2 Graph True Or False

Example 1. The equation of the straight line parallel to X axis is x = c (c is a constant)

Solution: The statement is False.

Example 2. (-8, 5) lies in the 3rd quadrant.

Solution: The statement is False.

Example 3. (6, 0) lies in X axis.

Solution: The statement is True.

Example 4. \(\frac{X}{2}-\frac{Y}{2}\) = 1 intersects Y axis at (0, 2).

Solution: The statement is True.

Example 5. The distance of the point (-a, -b) from X axis is a units. (where a, b > 0).

Solution: The statement is True.

Example 6. The distance of the point (8, 6) from the origin is 10 units.

Solution: The statement is True.

Example 7. y = -x is passing through origin.

Solution: The statement is True.

Example 8. 2x + 3y = 5 passes through origin.

Solution: The statement is False.

Example 9. The angle between the lines y = constant and x = constant is 90°.

Solution: The statement is True.

Example 10. The line joining the points (a, b) and (-a, -b) passes through the origin.

Solution: The statement is True.

Algebra Chapter 2 Graph Short Answer Type Questions

Example 1. Let us write the coordinates the point of intersection of the graph of equation 2x + 3y = 12 and the X axis.

Solution: At X axis ordinate = 0

∴ 2x + 0 = 12 or, x = 6

⇒ The point of intersection is (6, 0).

Example 2. Let us write the coordinates of the point of intersection of the graph of the equation 2x – 3y = 12 and the Y axis.

Solution: At Y axis, abscissa = 0

∴ 0 – 3y = 12 or, y = -4

⇒ The point of intersection is (0, -4).

Example 3. Let us write the distance of the point (6,-8) from X axis and Y axis.

Solution: Distance from X axis= 8 units.

⇒ Distance from Y axis = 6 units.

Example 4. Let us write the angle derived from the equation XY from the positive direction of X axis.

Solution: y = x straight lines make 45° angle with the positive side of X axis.

Example 5. Answer the following

1. ΔAPC =?
2. ΔBPD =?

Solution:

1. AC (54) unit = 1 unit
   height ΔAPC 3 units
   ΔAPC = \(\frac{1}{2}\).1.3 sq units
   = 1\(\frac{1}{2}\) sq units.
2. BD = (6 – 5) unit = 1 unit
   height of ΔBPD = 2 units
   ΔBPD = \(\frac{1}{2}\) x 1 x 2 sq units = 1 sq unit

Example 6. 2x + 3y = 11 intersects X axis at (α, β) then find α, β.

Solution: At X axis y = 0

∴ 2x + 3 x 0 = 11

⇒ or, x = +\(\frac{11}{2}\)

∴ The intersection point is (\(\frac{11}{2}\),0)

∴ α = \(\frac{11}{2}\), β = 0

Example 7. Find the point of intersection of the straight lines y = x and 3x – 2y = 0

Solution: By putting y = -x in 3x – 2y = 0, 3x – 2(-x) = 0

⇒ or, 5x = 0

⇒ or, x = 0 and y = 0

∴ The point of intersection is (0, 0)

Example 8. Find the point of intersection of x = 2, y = 3.

Solution: The straight line x = 2 is parallel to Y axis and the straight

⇒ line y = 3 is parallel to X axis.

∴ The point of intersection is (2, 3).

Example 9. Find the area of the triangle formed by the coordinate axes and the straight lines 2x + 3y = 6.

Solution: At X axis, y = 0

∴ 2x + 0 = 6, x = 3

⇒ The straight line intersects X axis at (3, 0)

⇒ Similarly at Y axis, Y = 0

∴ 2.0 + 3y = 6, y = 2

⇒ The straight line intersects Y axis at (0, 2)

⇒ D = \(\frac{1}{2}\) x 3 x 2 sq. units = 3 sq. units.

Arithmetic Chapter 2 Profit And Loss

⇒ Cost price: The amount paid to purchase an article is known as its cost price.

⇒  Selling price: The price at which an article is sold is known as its selling price.

⇒  The cost price and selling price are abbreviated as C. P. and S. P. respectively.

⇒  Profit: If S.P. > C. P. then the difference between S. P. and C. P. is called profit.

⇒ Loss: If C. P. > S. P. then the difference between C. P. and S. P. is called loss.

∴ Profit = Selling price (S. P.) – Cost price (C. P.) and Loss Cost price (C. P.) – Selling price (S. P.)

⇒ Marked price: While buying goods we have seen that on every article there is a price marked. This price is known as the marked price of the article.

⇒ Discount = Marked price x Rate of discount

⇒ S. P. = Marked price – Discount

⇒ Profit percentage = \(=\frac{\text { Total profit }}{\text { Cost price }}\) x 100

⇒ Loss percentage = \(=\frac{\text { Total loss }}{\text { Cost price }}\) x 100

⇒ Equivalent discount: On a particular principal the equivalent discount is equal to more than one successive discount on that principal.

⇒ The discount equivalent to successive discounts of a% and b% is (a + b – \(\frac{ab}{100}\))%

Read and Learn More  WBBSE Solutions For Class 9 Maths

Arithmetic Chapter 2 Profit And Loss True Or False

Example 1. If selling price of an article is smaller than the cost price, then there will be profit.

Solution: The statement is False.

Example 2. If S.P. and C.P. of an article are equal then there will be no profit or loss.

Solution: The statement is True.

Example 3. Ram purchased a pen for ₹50 and sold it to Shyam at a loss of 20% then the selling price of that pen was ₹40.

Solution: C.P. = ₹50 and S.P. = ₹40

Loss = ₹(50 – 40) = ₹10

Loss percentage = \(\frac{10}{50}\) x 100 = 20

∴ The statement is True.

Arithmetic Chapter 2 Profit And Loss Fill In The Blanks

Example 1. Profit percentage x ________ = Total profit x 100.

Solution: cost price (C. P.).

Example 2. Cost price = \(=\frac{100 \times}{100-\text { Loss percentage }}\)

Solution: Selling price.

Example 3. There is a ________ relation between cost price and selling price

Solution: Direct.

Arithmetic Chapter 2 Profit And Loss Short Answer Type Questions

Example 1. If 20% profit is on cost price, what is profit percentage on selling price?

Solution: If cost price is ₹100 then profit is ₹20

∴ Selling price = ₹(100+ 20) = ₹120

⇒ If selling price is ₹120 then profit is ₹20

⇒ If selling price is ₹1, then profit is ₹\(\frac{20}{120}\)

⇒ If selling price is ₹100, then profit is ₹\(\frac{20}{120}\) x 100

= ₹\(\frac{50}{3}\) = ₹16\(\frac{2}{3}\)

∴ Profit is 16\(\frac{2}{3}\)% on selling price.

Example 2. If 20% profit is on selling price, what is the profit percentage on cost price?

Solution: If S.P. is ₹100 then profit is ₹20

∴ C.P. = ₹(100 – 20) = ₹80

⇒ If C.P. is ₹80, then profit is ₹20

⇒ If C.P. is ₹1, then profit is ₹\(\frac{20}{80}\)

⇒ If C.P. is ₹100, then profit is ₹(\(\frac{20}{80}\) x 100) = ₹25

∴ 25% profit on cost price.

Example 3. By selling 110 mangoes, if the cost price of 120 mangoes has been got, what will be the profit percentage?

Solution: Let S.P. of 110 mango is ₹x

⇒ S.P. of 1 mango is ₹\(\frac{x}{110}\)

⇒ According to condition, C.P. of 120 mangoes is ₹x [x > 0]

∴ C.P. of 1 mango is ₹\(\frac{x}{120}\)

⇒ Profit = \(₹\left(\frac{x}{110}-\frac{x}{120}\right)\)

= \(₹\left(\frac{12 x-11 x}{1320}\right)=₹ \frac{x}{1320}\)

⇒ If C.P. is \(₹ \frac{x}{120}\) then profit is \(₹ \frac{x}{1320}\)

⇒ If C.P. is 1, then profit is \(₹\left(\frac{x}{1320} \times \frac{120}{x}\right)\)

⇒ If C.P. is 100, then profit is \(₹\left(\frac{120 \times 100}{1320}\right)\) = \(\frac{100}{11}\) = 9\(\frac{1}{11}\)

∴ Profit is 9\(\frac{1}{11}\).

Example 4. To submit electricity bill in due time, 15% discount can be obtained. Sumanbabu has got 54 as discount for submission of electricity bill in due time. How much was his electricity bill?

Solution: Let, the electricity bill of Sumanbabu was ₹x

⇒ Discount = \(₹\left(x \times \frac{15}{100}\right)=₹ \frac{3 x}{20}\)

⇒ According to question, \(₹ \frac{3 x}{20}\) = 54

⇒ x = \(\frac{54 \times 20}{3}\)

⇒ x = 360

∴ The electricity bill was ₹360

Example 5. A commodity is sold at ₹480 with a loss of 20% on selling price, what is the cost price of the commodity?

Solution: If selling price of a commodity is ₹100 then loss is ₹20.

⇒ C.P. = ₹(100+20) = ₹120

⇒ If S.P. is ₹100, then C.P. is ₹120

⇒ If S.P. is ₹1 then C.P. is \(₹ \frac{120}{100}\)

⇒ If S.P is ₹480 then C.P. is ₹\(\frac{120 \times 480}{100}\) = ₹576

∴ Cost price of the commodity is ₹576.

Example 6. If a commodity is sold with successive discounts of 20% and 10%, what will be the equivalent discount?

Solution: Let the marked price of the commodity is ₹100

⇒ Then first discount is ₹20

⇒ The net price after 1st discount = ₹(100 – 20) = ₹80

⇒ Second discount = 10% of ₹80 = \(₹ \left(80 \times \frac{10}{100}\right)\) = ₹8

⇒ Total discount = ₹(20 + 8) = ₹28

∴ The equivalent discount is 28%.

Example 7. By selling a clock for 180, Rohit loses 10%, for what amount should be sell it as to gain 10%. [By proportion]

Solution: The loss is 10%

If C.P. of the clock is ₹100, then S.P. will be ₹(100 – 10) = ₹90

In mathematical language, the problem is,

⇒ S.P.(₹)
90
180

⇒ C.P.(₹)
100
?

⇒ The relation between S.P. and C.P. is direct.

∴ The direct proportion is, 90: 180 100: ? (The required C.P.)

∴ The required cost price = \(₹ \frac{180 \times 100}{90}=₹ 200\)

⇒ Rohit wants to make 10% profit

⇒ In mathematical language, the problem is

C.P(₹)
100
200

S.P. (₹)
100+ 10 = 110
?

⇒ The relation between S.P. and C.P. is direct

∴ The direct proportion is, 100: 200 : : 100:? (The required C.P.)

∴ The required selling price = \(₹ \frac{200 \times 110}{100}\) = ₹220

∴ To get 10% profit, Rohit has to sell the clock at ₹220

Example 8. Some toffees are bought at 15 for a rupee and the same number at 10 a rupee. Find the gain or loss percent.

Solution: C.P. of 15 toffees is ₹1

⇒ C.P. of 1 toffee is ₹\(\frac{1}{5}\)

⇒ S.P. of 10 toffees is ₹1

⇒ S.P. of 1 toffee is ₹\(\frac{1}{5}\)

⇒ Profit = \(₹\left(\frac{1}{10}-\frac{1}{15}\right)=₹ \frac{1}{30}\)

⇒ Profit % = \(\frac{\frac{1}{30}}{\frac{1}{15}} \times 100=\frac{15}{30} \times 100=50\)

∴ The percentage profit of toffees is 50.

Example 9. Akash sells a shirt at a loss of 20%. Had he sold the shirt for 200 more, he would have earned a profit of 5%. Determine the cost price of the shirt.

Solution: Let, the C.P. of the shirt is ₹x [x > 0]

⇒ Loss = 20% of ₹x = \(₹\left(x \times \frac{20}{100}\right)=₹ \frac{x}{5}\)

⇒ S.P = \(₹\left(x-\frac{x}{5}\right)=₹ \frac{4 x}{5}\)

⇒ Had Akash sold the shirt for ₹200 more, i.e. \(₹\left(\frac{4 x}{5}+200\right)\), he would have earned a profit of 5%

∴ x + x x \(\frac{5}{100}\) = \(\frac{4x}{5}\) + 200

⇒ x + \(\frac{x}{20}\) – \(\frac{4x}{5}\) = 200

⇒ \(\frac{20 x+x-16 x}{20}=200\)

⇒ 5x = 200 x 20

⇒ x = \(\frac{200 \times 20}{5}\)

⇒ x = 800

∴ Cost price of the shirt is ₹800

Example 10. A dishonest businessman defrauds by false balance, to the extent of 10% both in buying and in selling his goods. Find the actual gain percent of the businessman.

Solution: Since the businessman defrauds to the extent of 10% in buying.

⇒ So he takes goods of ₹110 in exchange of ₹100

⇒ Again, the businessman sells goods of ₹100 at ₹110

⇒ the businessman sells goods of ₹1 at ₹\(\frac{110}{100}\)

⇒ the businessman sells goods of ₹110 at \(₹ \frac{110 \times 110}{100}\) = ₹121

∴ The businessman finally gets ₹121 in exchange of ₹100

∴ The actual gain percent = (121 – 100) = 21.

Statistics Chapter 1 Mean

⇒ An average or a central value of a data or a statistical series is the value of the variable which describes the characteristics of the entire data or the associated frequency distribution.

⇒ Central position: If the numbers of data are arranging in ascending order then the middle number / or the positions of nearly numbers is called the central position.

⇒ There are three measures of central tendency:

1. Mean
2. Median
3. Mode.

⇒ Arithmetic mean can be defined in the following three cases separately:

1. Individual observations (or ungrouped data).
2. Discrete frequency distribution (or grouped data)
3. Grouped or continuous frequency distribution.

⇒ Arithmetic Mean of individual observation (or ungrouped data)

Definition: If x₁, x₂, x₃ ………., x_n are n values of a variable X, then the arithmetic mean or simply the mean of these values is denoted by \(\overline{\mathrm{X}}\) and is defined as

Read and Learn More WBBSE Solutions for Class 10 Maths

= \(\frac{1}{n} \sum_{i=1}^n x_i\) [symbol ‘∑’ reading as capital sigma]

or, simply \(\bar{X}=\frac{\sum x_1}{n}\)

Arithmetic mean of grouped data or discreate frequency distribution

In a discreate frequency distribution, the arithmetic mean may be computed by any one of the following methods

1. Direct method,
2. Short-cut method,
3. Step deviation method.

⇒ Direct method: If a variate X takes values x₁, x₂, x₃ ………., x_n with corresponding frequencies ƒ₁, ƒ₂, ƒ₃ ……….,ƒ_n respectively, then the arithmetic mean of these values is given by

= \(\frac{\sum_{i=1}^n f_i x_i}{\sum_{i=1}^n f_i} \text { or simply } \overline{\mathrm{X}}=\frac{\sum f_i x_i}{\sum f_i}\)

⇒ Short-cut method: Let x₁, x₂, x₃ ………., x_n be values of a variable X with corresponding frequencies respectively.

Taking deviations about an arbitary point ‘a’ we have

⇒ \(\sum_{i=1}^n f_i d_i=\sum_{i=1}^n f_i\left(x_i-a\right)\)

⇒ \(\sum_{i=1}^n f_i d_i=\sum_{i=1}^n f_i x_i-a \sum_{i=1}^n f_i \quad \text { [as a is constant] }\)

⇒ \(\frac{1}{\sum_{i=1}^n f_i} \sum_{i=1}^n f_i d_i=\frac{\sum_{i=1}^n f_i x_i}{\sum_{i=1}^n f_i}-\frac{a \sum_{i=1}^n f_i}{\sum_{i=1}^n f_i}\)

⇒ \(\frac{1}{\sum_{i=1}^n f_i} \sum_{i=1}^n f_i d_i=\overline{\mathrm{X}}-a\)

⇒ \(\overline{\mathrm{X}}=a+\frac{\sum_{i=1}^n f_i d_i}{\sum_{i=1}^n f_i}\)

or, simply \(\overline{\mathrm{X}}=a+\frac{\sum f_i d_i}{\sum f_i}\)

[a is known as assumed mean and is generally chosen in such a way that the deviation are small]

⇒ Step-deviation method:

Mean \((\overline{\mathbf{X}})=a+h \frac{\sum f_i u_i}{\sum f_i}\)

where \(u_i=\frac{x_i-\dot{a}}{n}\) [n = class size]

Class 10 Maths Statistics Chapter 1 Solutions

Statistics Chapter 1 Median

Definition: Median of a distribution is the value of the variable which divides the distribution into two equal parts i.e. it is the value of the variable such that the number of observations above.

It is equal to the number of observations below it.

⇒ Median of ungrouped data: If the values x_i in the raw data arranged in order of increasing or decreasing magnitude, then the middle, most value in the arrangement is called the median.

Let x₁, x₂, x₃ ………., x_n be the n values of a variable. X arranged in x₁, x₂, x₃ ………., x_n [where x₁< x₂ < x₃ ………., < x_n]

[Few may be equal among the values]

1. If n is odd, median is the value of \(\left(\frac{n+1}{2}\right)\)th observation

∴ Median = \(X_{\frac{n+1}{2}}\) when n is odd

2. If n is even the median is the mean of the \(\frac{n}{2}\)th and the (\(\frac{n}{2}\) + 1)th

∴ Median = \(=\frac{X_n+X_n \frac{2}{2}}{2}\), when n is even

⇒ Median of a grouped data:

Median = \(=l+\left[\frac{\frac{n}{2}-c_f}{f}\right] \times h\)

Where, l = lower limit of median class

ƒ = frequency of median class

n = number of observation

c_ƒ = cumulative frequency of Class preceding the median class

n = class size of the median class

Wbbse Class 10 Maths Statistics Solutions

Statistics Chapter 1 Mode

Mode is the value that occurs most frequently in a set of observations and around which the other items of the set cluster densely.

Thus, the mode of frequency distribution is the value of the variable which has the maximum frequency

Mode = \(l+\frac{f_1-f_0}{2 f_1-f_0-f_2} \times h\)

Where, l = lower limit of the modal class

h = length of the modal class

ƒ₁ = frequency of the modal class

ƒ₀= frequency of the class preceding the modal class

ƒ₂ = frequency of the class succeeding the modal class

Relation between mean, median, and mode:

Mode = 3 x median – 2 x mean

Statistics Chapter 1 Ogive

⇒ Ogive: Ogives are graphs that can be used to determine how many data values lie above or below a particular value in a data set.

Statistics Chapter 1 Mean Median Ogive Mode True Or False

Example 1. Value of mode of data 2, 3, 9, 10, 9, 3, 9 is 10

Solution: Let us write the numbers of given data in ascending order in magnitude.

2, 3, 3, 9, 9, 9, 10

As 9 occurs a maximum number of times.

∴ The mode of data is 9

∴ The statement is false.

Example 2. Median of data 3, 14, 18, 20, and 5 is 18

Solution: Arranging the number of the given data in ascending order in magnitude, we have,

3, 4, 5, 18, 20

Here n = 5 [i.e. n is odd]

∴ Median = \(\frac{5+1}{2}\) th term = 3rd term = 5

∴ The given statement is false.

Example 3. If the arithmetic mean of 7, 10, x – 2, and x + 3 is 9 then the value of x is 9.

Solution: \(\text { Mean }(\bar{X})=\frac{7+10+x-2+x+3}{4}=9\)

⇒ 2x + 18 = 36 ⇒ x = 9

∴ The statement is true.

Example 4. If the median of arranging the ascending order of data 6, 7, x – 2, x, 17, 20 is 16 then the value of x is 18.

Solution: Here n = 6 [i.e. n is even]

∴ Median = \(\frac{1}{2}\)[\(\frac{1}{2}\) th observation + (\(\frac{1}{2}\) + 1) ovservation]

= \(\frac{1}{2}\) [3rd observation + 4th observation]

= \(\frac{1}{2}\) (x – 2 + x) = x – 1

According to question x- 1 = 16

⇒ x = 17

∴ The statement is false.

Statistics Class 10 Solutions

Statistics Chapter 1 Mean Median Ogive Mode Fill In The Blanks

Example 1. Mean, median, and mode are the measures of ______

Solution: centrally.

Example 2. If Mean of x₁, x₂, x₃ ……….,x_n is \(\bar{X}\), then mean of ax₁, ax₂, ax₃ ……….,ax_n is _____

Solution: If mean of x,, x2, is \(\bar{X}\) then

The mean of \(a x_1, a x_2, \ldots \ldots, a x_n is \frac{a x_1+a x_2+\cdots \cdots+a x_n}{n}\)

= \(\frac{a\left(x_1+x_2+\cdots \cdots+x_n\right)}{n}=a \bar{x}\)

Example 3. At the time of finding the arithmetic mean by the step-deviation method, the lengths of all classes are _________

Solution: equal.

Example 4. The arithmetic mean of first n natural numbers is _________

Solution: \(\frac{n+1}{2}\)

Example 5. The median of a frequency distribution is determine by ________ graph.

Solution: Ogive.

Class 10 Statistics Chapter 1 Solved Examples

Statistics Chapter 1 Mean Median Ogive Mode Short Answer Type Question

Example 1. Find the difference between upper-class limit in median class and lower class limit of modal class of the frequency distribution table

Solution:

N = ∑ƒ=77

At first, we locate the class where the cumulative frequency is equal to \(\frac{n}{2}\) or greater than \(\frac{n}{2}\) in the above frequency distribution table.

\(\frac{n}{2}\) = \(\frac{77}{2}\) = 38.5

∴ The cumulative frequency of the class is 42 which is just greater than 38.5 and the corresponding class is (125 – 145)

∴ The medians class is (125 – 145)

∴ The upper-class limit in median class is 145

As highest frequency in the above frequency distribution table is 20.

∴ The modal class is (125 – 145)

∴ Lower class limit of modal class is 125.

The difference between upper class limit in median class and lower class limit of modal class is (145 – 125) or 20.

Example 2. The following frequency distribution shows the time taken to complete 100 metre hardle race of 150 athletics

Find the number of athletics who complete the 100-metre hardle race within 14.6 seconds.

Solution: The number athletics are (2 + 4 + 5 + 71) = 82

Example 3. The mean of a frequency distribution is 8.1, if \(\sum \dot{f_I} x_i=132+5 \mathrm{k} \text { and } \sum f_i=20\); find the value of k.

Solution: Mean \(\bar{x}=\frac{\sum {f_i}{x_i}}{\sum f_i}=\frac{132+5 k}{20}\)

According to the question = \(\frac{132+5 \mathrm{k}}{20}=8 \cdot 1 \\\)

⇒ \(132+5 \mathrm{k}=162\)

⇒ \(\mathrm{k}=\frac{162-132}{5}=6\)

Wbbse Class 10 Statistics Notes

Example 4. If \(u_i=\frac{x_i-25}{10}, \Sigma f_i u_i=20 and \Sigma f_i=100\), find the value of \(\bar{x}\).

Solution: If assumed mean = a and class size = h then [/latex]u_i=\frac{x_i-a}{h}[/latex]

∴ \(\frac{x_i-a}{h}=\frac{x_i-25}{10}\)

equating both sides, we get a = 25 and h = 10

∴ Mean \((\bar{x})=a+\frac{\sum f_i u_i}{\sum f_i} \times h\)

= 25 + \(\frac{20}{100}\) x 10

= 25 + 2 = 27

∴ The value of \(\bar{X}\) is 27.

Example 5. Write the modal class from the above frequency distribution table.

Solution:

Highest frequency in above frequency distribution table is 30

∴ The modal class is (30- 40)

Example 6. A table of weight of 50 students are given below

Find the mean of their weights by direct method.

Solution:

∴ Mean weight of students = \(\frac{\sum f_i x_i}{\sum f_i}\)

= \(\frac{1919}{50} \mathrm{~kg}=38.38 \mathrm{~kg}\)

Example 7. The marks obtained by 80 students of class nine in mathematics are given in the table below

Find the average marks of 80 students bj using assumed mean method.

Solution: Let assumed mean (a) = 60

∴ Average marks = \(a+\frac{\sum f_i d_i}{\sum f_i}\)

= 60 + \(\frac{560}{80}\)

= 60 + 7 = 67

Measures Of Central Tendency Class 10 Solutions

Example 8. Find the mean of the following data by using direct method.

Solution:

∴ Mean \(\bar{x}=\frac{\sum f_i x_i}{\sum f_i}\)

= \(\frac{1780}{30}\) = 59.33 (approx)

Example 9. Find the mean of the following data by using the assumed mean method.

Solution: Let assumed mean (a) = 25

∴ Mean \((\overline{\mathrm{X}})=a+\frac{\sum f_i d_i}{\sum f_i}\)

= \(25+\frac{-30}{60}\)

= 25 – 0.5 = 24.5

Example 10. Find the mean of the following data given below by using the step-deviation method.

Solution: Let the assumed mean (a) = 52.5

class size (h) = 15

∴ Mean \((\bar{X})=a+\frac{\sum f_i u_i}{\sum f_i} \times h\)

= \(52 \cdot 5+\frac{-10}{50} \times 15\)

= 52.5 – 3 = 49.5

Example 11. Height of some students in cm are 155, 145, 148, 144, 146, 150, 152, 147. Find their median.

Solution: Arranging their heights in ascending order we get,

144 cm, 145 cm, 146 cm, 147 cm, 148 cm, 150 cm, 152 cm, 155 cm, 156 cm.

Here, n = 9 i.e. n is odd

∴ Median of height = \(\frac{n+1}{2}\)th value

= \(\frac{9+1}{2}\)th value = 5 th value = 148 cm.

Class 10 Maths Statistics Important Questions

Example 12. The marks obtained by 10 students of class 9 in Bengali are 88, 65, 80, 52, 38, 70, 44, 75, 62, and 35. Find the median of marks.

Solution: Arranging the marks in ascending order we get,

35, 38, 44, 52, 62, 65, 70, 75, 80, 88

Here, n = 10 i.e. n is even

∴ Median = \(\frac{1}{2}\)[\(\frac{10}{2}\)th value + (\(\frac{1}{2}\) + 1)th value]

= \(\frac{1}{2}\)[5th value + 6th value]

= \(\frac{1}{2}\)(62 + 65) = \(\frac{127}{2}\) = 63.5

∴ Median of marks is 63.5.

Example 13. Find the median from the frequency distribution table given below

Solution:

Here n = ∑ƒ = 37 i.e. n is odd

∴ Median = (\(\frac{n+1}{2}\))th observation

= (\(\frac{37+1}{2}\))th observation

= 19 th observation = 42

Example 14. Find the median from frequency distribution table given below:

Solution:

n = ∑ƒ = 100 i.e. n is even

∴ Median = \(\frac{1}{2}\) [\(\frac{n}{2}\) th observation + (\(\frac{n}{2}\) + 1) th observation]

= \(\frac{1}{2}\)[\(\frac{100}{2}\) th observation + (\(\frac{100}{2}\) + 1) th observation]

= \(\frac{1}{2}\) [50th observation + 51th observation]

= \(\frac{1}{2}\)[42 + 4] = \(\frac{1}{2}\) x 8 = 4

Example 15. Find the median from the frequency distribution table given below

Solution:

n = 50,

∴ \(\frac{n}{2}\) = \(\frac{50}{2}\) = 25

(60 – 80) is the class whose cumulative frequency 38 is just greater than 25

Median = \(l+\left[\frac{\frac{n}{2}-c f}{f}\right] \times h\)

Here, l = lower limit of median class

n = number of observation

ƒ = frequency of median class

c_ƒ = cumulative frequency of class preceding the median class

h = class size of the median class

∴ Median = \(l+\left[\frac{\frac{n}{2}-\mathrm{C}_f}{f}\right] \times h\) [ l = 60, n = 50, C_ƒ= 24, ƒ = 14, h = 20]

= \(60+\left[\frac{\frac{50}{2}-24}{14}\right] \times 20\)

= 60 + \(\frac{1}{14} \times 20\) = 60 + 1.42 (approx) = 61.42 (approx)

Class 10 Maths Board Exam Solutions

Example 16. Find the mode of the data given below

4, 6, 10, 5, 8, 12, 5, 10, 6, 7, 5, 9, 11, 5, 12, 6, 8, 5, 12, 5

Solution: Arranging the numbers of given data in ascending order in magnitude.

4, 5, 5, 5, 5, 5, 5, 6, 6, 6, 7, 8, 8, 9, 10, 10, 11, 12, 12, 12

As 5 occurs maximum number of times.

∴ The mode of data = 5

Example 17. Find the mode of frequency distribution table given below

Solution: The modal class of given frequency distribution table is (30 – 40)

[As maximum number of frequency is 15]

Reqired mode = \(l+\left(\frac{f_1-f_0}{2 f_1-f_0-f_2}\right) \times h\)

Here, l = lower limit of the modal class = 30

h = length of the modal class = 10

ƒ₁ = Frequency of the rhodal class =15

ƒ₀ = Frequency of the class preceding the modal class = 10

ƒ₂ = Frequency of the class succeeding the modal class = 8

∴ Mode = \(30+\left(\frac{15-10}{2 \times 15-10-8}\right) \times 10\)

= 30 + \(\frac{5}{12}\) x 10

= 30 \(+\frac{50}{12}\)

∴ Mode = 30 + 4.17 = 34.17(approx).