Marksparks .arkansas

WBBSE Class 10 Maths Mensuration Chapter 1 Rectangular Parallelopiped Or Cuboid Multiple Choice Questions

Example 1. The inner volume of a cuboidal box is 440 c.c. and the area of the inner base is 88 sq. The inner height is

1. 4 cm
2. 5 cm
3. 3 cm
4. 6 cm

Read And Learn Also WBBSE Class 10 Maths Multiple Choice Questions

Solution: base x height = volume

∴ height = \(\frac{440}{80}\) = 5

∴ The correct answer is 2. 5 cm

Example 2. The length, breadth and height of a cuboidal hole are 40 m, 12 m, and 16 m respectively. The number of planes having a height of 5 m, a breadth of 4 m and a thickness of 2 m can be kept in the hole is

1. 190
2. 192
3. 184
4. 180

Solution: Number of Planks = \(\frac{\text { volume of the hole }}{\text { volume of a plank }}=\frac{40 \times 12 \times 16}{5 \times 4 \times 2}=192\)

∴ The correct answer is 2. 192

Surface Areas And Volumes Mcqs Class 10

Example 3. The total surface area of a cube is 384 sq. m, the volume of the cube is

1. 64 cu.m
2. 216 cu.m
3. 256 cu.m
4. 512 cu.m

Solution: 6a² = 384

or, a² = \(\frac{384}{6}\) = 64

∴ a = 8

volume = 8³ cu.m = 512 cu. m

∴ The correct answer is 4. 512 cu.m

Example 4. The ratio of the volume of the two cubes is 1: 27, and the ratio of the total surface area is

1. 1: 3
2. 1: 8
3. 1: 7
4. 1: 9

Solution: Let the lengths be a₁, and a₂ units respectively

∴ \(\frac{a_1^3}{a_2^3}=\frac{1}{27}\)

⇒ or, \(\frac{a_1}{a_2}=\frac{1}{3}\)

⇒ or, \(\frac{4 a_1^2}{4 a_2^2}=\frac{4}{4}: \frac{1}{9}=1: 9\)

The correct answer is 4. 1: 9

Surface Areas And Volumes Mcqs Class 10

Example 5. If the total surface area of a cube is S sq. unit and the length of the diagonal is d unit, then the relation between S and d is

1. S = 6d²
2. 3S = 7d
3. S³ = d²
4. d² = \(\frac{S}{2}\)

Solution: 6a² = S, √3a = d

∴ \(6\left(\frac{d}{\sqrt{3}}\right)^2=\mathrm{S}\)

⇒ or, \(\frac{6 d^2}{3}=\mathrm{S}\)

⇒ or, 2d² = S

⇒ or, \(d^2=\frac{S}{2}\)

∴ The correct answer is 4. \(d^2=\frac{S}{2}\)

Example 6. If length of the diagonal of each surface of a cube is 8√2 cm, then the length of the diagonal of the cube is

1. 5√3 cm
2. 6√3 cm
3. 7√3 cm
4. 8√3 cm

Solution: side x √2 = 8√2 cm or, side = 8cm

⇒ Length of the diagonal = 8√3 cm

∴ The correct answer is 4. 8√3 cm

Example 7. Sum of the edges of a cube is 60 cm. Volume will be

1. 85 cu. cm
2. 110 cu. cm
3. 125 cu. cm
4. 100 cu. cm

Solution: 12a = 60, a = 5

∴ Volume = 5³ cu. cm = 125 cu. cm

∴ The correct answer is 3. 125 cu. cm

Class 10 Mensuration Chapter 1 Mcqs With Answers

Example 8. Length of a diagonal of a surface of a cuboid is \(\sqrt{a^2+b^2}\) unit and the height is c unit. Length of the diagonal of the cuboid is

1. \(\sqrt{a^2+b^2+c^2}\) unit
2. \(\sqrt{abc}\)
3. (a² + b² + c²) unit
4. abc unit

Solution: Length of the diagonal = \(\sqrt{\text { length }^2+(\text { breadth })^2+(\text { height })^2}\)

= \(\sqrt{a^2+b^2+c^2}\) unit

∴ The correct answer is 1. \(\sqrt{a^2+b^2+c^2}\) unit

Example 9. No of vertices, edges and surfaces of a cuboid are x, y, and z respectively. Then x – y + z =

1. 1
2. 2
3. 3
4. 4

Solution: x = 8, y = 12, z = 6

∴ x-y + z = 8-12 + 6 = 2

∴ The correct answer is 2. 2

Surface Areas And Volumes Mcqs With Solutions

Example 10. The length of the edges of a cubical tin pot is 30 cm. What maximum quantity of water in litres will it contain?

1. 27
2. 27000
3. 1000
4. None of these

Solution: Volume = (30 cm)³

= 27000 cu.cm = 27 litres

∴ The correct answer is 1. 27

WBBSE Class 10 Maths Mensuration Chapter 2 Right Circular Cylinder Multiple Choice Questions

Example 1. If the length of radii of two solid right circular cylinders are in the ratio 2 : 3 and their heights are in the ratio 5 : 3, the ratio of their lateral surface is

1. 2: 5
2. 8: 7
3. 10: 9
4. 16: 9

Solution: Let radii of r_1,r₂ units and that of height be h_1,h₂ units respectively.

∴ Required ratio = \(\frac{2 \pi r_1 h_1}{2 \pi r_2 h_2}=\frac{2}{3} \times \frac{5}{3}=10: 9\)

∴ Answer is 3. 10: 9

Example 2. If the length of radii of two solid right circular cylinders are in the ratio 2 : 3 and their height in the ratio 5 : 3, then the ratio of their volume is

1. 27: 20
2. 20: 27
3. 4: 9
4. 9: 4

Solution: Let radii be r_1,r₂ units and that of height be h_1,h₂ units respectively.

Read And Learn Also WBBSE Class 10 Maths Multiple Choice Questions

Required ratio = \(\frac{\pi r_1^2 h_1}{\pi r_2^2 h_2}=\left(\frac{2}{3}\right)^2 \times \frac{5}{3}=\frac{4}{9} \times \frac{5}{3}=20: 27\)

∴ Answer is 2. 20: 27

Class 10 Maths Mensuration Chapter 2 MCQs

Example 3. If volumes of two solid right circular cylinder are same and their height are in the ratio 1: 2, then the ratio of length of radii is

1. 1:√2
2. √2: 1
3. 1: 2
4. 2:1

Solution: Let radii be r_1,r₂ units and that of height h_1,h₂ units.

∴ \(\pi r_1{ }^2 h_1=\pi r_2{ }^2 h_2\)

or, \(\left(\frac{r_1}{r_2}\right)^2=\frac{h_2}{h_1}=\frac{2}{1}\)

∴ r₁: r₂ = √2: 1

∴ Answer is 2. √2: 1

Example 4. In a right circular cylinder, if the length of radius is halved and height is doubled, volume of cylinder will be

1. Equal
2. Double
3. Half
4. 4 times

Solution: volume = πr²h cubic unit

changed volume = \(\pi\left(\frac{r}{2}\right)^2\) .2h cubic unit = \(\frac{\pi r^2 h}{2}\) cubic units

∴ Answer is 3. Half

Example 5. If the length of radius of a right circular cylinder is doubled and height is halved, the lateral surface area will be

1. Equal
2. Double
3. Half
4. 4 times

Solution: Volume πr²h c.u

changed volume = π(2r)².\(\frac{h}{2}\) c.u.= 2πr²h cubic units.

∴ Answer is 2. Double

Example 6. Diameter and height of two solid right circular cylinders are 8 units and 3(h – 1) units respectively and the volumes are equal, then h =?

1. 9
2. 2
3. 17
4. 19

Solution: \(\pi\left(\frac{8}{2}\right)^2 \cdot 3(h-1)=\pi\left(\frac{12}{2}\right)^2 \times(h+5)\)

or, 48 (h – 1) = 36 (h + 1) or, 12h = 228

∴ h = 19

∴ Answer is 4. 19

Wbbse Class 10 Maths Mensuration Notes

Example 7. Volume of a cylindrical tank is 6160 cubic metro and radius is 14 metro. Depth is

1. 8 metre
2. 10 metre
3. 14 metre
4. 16 metre

Solution: π (14)².h = 6160 or, h = \(\frac{6160 \times 7}{22 \times 14 \times 14}\) = 10

∴ Answer is 2. 10 metre

Example 8. No. of coins with diameter 3 cm and 0.25 cm thickness from a cuboid of dimension 11 cm x 9 cm x 6 cm will be

1. 320
2. 330
3. 336
4. 340

Solution: No. of coins = \(\frac{11 \times 9 \times 6}{\frac{22}{7} \times \frac{3}{2} \times \frac{3}{2} \times 0.25}\) = 336

∴ Answer is 3. 336

Class 10 Mensuration Chapter 2 Mcqs With Answers

Example 9. Area of the bane and lateral surface area of a cylinder of radius 8 cm are equal. Height will be

1. 3 cm
2. 4 cm
3. 5 cm
4. 6 cm

Solution: πr² = 2πrh

⇒ h = \(\frac{r}{2}\) = \(\frac{8}{2}\) = 4

∴ Answer is 2. 4 cm

Example 10. Volume of the hollow cylinder of outer radius R, inner radius r and height h will be

1. π (R² + r²)h
2. π (R² – r²)h
3. \(\frac{\pi}{2}\)(R² – r²)h
4. \(\frac{\pi}{2}\)(R² + r²)h

Solution: Answer is 2. π (R² – r²)h

WBBSE Class 10 Maths Mensuration Chapter 3 Right Circular Cone Multiple Choice Questions

Example 1. If the slant height of a right circular cone is 15 cm. and the length of the base diameter is 16 cm, then the lateral surface are is

1. 60π cm²
2. 68π cm²
3. 120π cm²
4. 130π cm²

Solution: Lateral surface area = πrl

= π.\(\frac{16}{2}\).15 = 120 π cm²

∴ Answer is 3. 120π cm²

Example 2. If the ratio of the volumes of two right circular cones is 1: 4 and the ratio of the radii of their bases is 4: 5, then the ratio of the their height is

1. 1:5
2. 5: 4
3. 25: 16
4. 25: 64

Solution: \(\frac{\frac{1}{3} \pi r_1^2 h_1}{\frac{1}{3} \pi r_2^2 h_2}=\frac{1}{4}\)

⇒ or, \(\left(\frac{4}{5}\right)^2 \cdot \frac{h_1}{h_2}=\frac{1}{4}\)

⇒ or, \(\frac{h_1}{h_2}=\frac{25}{64}\)

∴ Answer is 4. 25: 64

Read And Learn Also WBBSE Class 10 Maths Multiple Choice Questions

Example 3. Keeping the radius of a right circular cone same if the height of it is increased twice, the volume of it will be increased by

1. 100%
2. 200%
3. 300%
4. 400%

Solution: \(\frac{\frac{1}{3} \pi r^2(2 h)}{\frac{1}{3} \pi r^2 h}=2\)

⇒ Increase = (200- 100)% = 100%

∴ Answer is 1. 100%

Combination Of Solids Mcqs With Solutions Class 10

Example 4. If each of radius and height of a cone is the volume increased by twice of its length will be

1. 3 times
2. 4 times
3. 6 times
4. 8 times of previous one

Solution: \(\frac{\frac{1}{3} \pi(2 r)^2 \cdot 2 h}{\frac{1}{3} \pi r^2 h}=8\)

∴ Answer is 4. 8 times of previous one

Example 5. If the length of the radius of a cone is \(\frac{r}{2}\) units and slant height of it is 2l unit, then the total surface area is

1. 2πr (l + r) sq. u
2. πr\((l+\frac{r}{4})\) sq. u
3. πr (h + r) sq. u
4. 2πrl sq. u

Solution: Answer is 2. πr\((l+\frac{r}{4})\) sq. u

Example 6. Length of the radius and slant height of a cone are 1.5 m and 2 mt respectively. The area of curved sharface is

1. 2π sq. m
2. 3π sq. m
3. 4π sq. m
4. 5π sq. m

Solution: Required area = π x (1.5) x 2 sq. m = 3π sq. m

∴ Answer is 2. 3π sq. m

Wbbse Class 10 Maths Mensuration Notes

Example 7. Height and length of the radius of a cone are 21 cm and 12 cm. Its volume will be

1. 4710 cu. cm
2. 9504 cu. cm
3. 3168 cu cm
4. none of these

Solution: Volume = \(\frac{1}{3}\) x \(\frac{22}{7}\) x(12)² x 21 cu. cm

= 3168 cu. cm

∴ Answer is 3. 3168 cu cm

Example 8. Ratio of volumes and length of the diameters are 1: 4 and 4: 5. Ratio of height will be

1. 5: 8
2. 25: 8
3. 5: 64
4. 25: 64

Solution: \(\frac{V_1}{V_2}=\frac{1}{4}=\frac{\frac{1}{3} \pi r_1^2 h_1}{\frac{1}{3} \pi r_2{ }^2 h_2}=\left(\frac{r_1}{r_2}\right)^2 \times \frac{h_1}{h_2}\)

∴ \(\frac{h_1}{h_2}=\frac{25}{64}\), \(h_1: h_2=\frac{25}{64}\)

∴ Answer is 4. 25: 64

Class 10 Maths Chapter 3 Mensuration Solutions

Example 9. Length of the radius of a cone is increased by 20%. Keeping height the same. The percentage increase of volume will be

1. 44%
2. 33%
3. 22%
4. 11%

Solution: Initial volume = \(\frac{1}{3}\)πr²h cu. unit

Changed volume = \(\frac{1}{3} \pi\left(\frac{120 r}{100}\right)^2 \cdot h\) cu. unit

= \(\frac{1}{3} \pi \frac{36 r^2}{25} h\) cu. unit

Volume increased = \(\frac{\frac{1}{3} \pi \frac{36 r^2}{25} h-\frac{1}{3} \pi r^2 h}{\frac{1}{3} \pi r^2 h} \times 100 \%\)

= \(\frac{36-25}{25} \times 100 \%\) = 44%

∴ Answer is 1. 44%

Example 10. Volume of the biggest cone made from a cube of length h unit is

1. \(\frac{\pi}{4} h^3 \text { cu. u }\)
2. \(\frac{\pi}{8} h^3 \text { cu. u }\)
3. \(\frac{\pi}{12} h^3 \text { cu. u }\)
4. \(\frac{\pi}{16} h^3 \text { cu. u }\)

Solution: Volume = \(\frac{1}{3} \pi\left(\frac{h}{2}\right)^2 h \text { cu. } \mathrm{u}=\frac{\pi}{12} h^3 \text { cu. u }\)

∴ Answer is 3. 22%

WBBSE Class 10 Maths Trigonometry Chapter 1 Concept Of Measurement Of Angle Multiple Choice Questions

Example 1. The end point of the minute hand of a clock rotates in 1 hour

1. \(\frac{\pi^c}{4}\)
2. \(\frac{\pi^c}{2}\)
3. π^c
4. 2π^c

Solution: The end point of the minute hand of a clock rotates in 1 hour is 360°

Read And Learn Also WBBSE Class 10 Maths Multiple Choice Questions

180° = π^c

∴ The correct answer is 4.

Example 2. \(\frac{\pi}{6}\) radian equal to

1. 60°
2. 45°
3. 90°
4. 30°

Solution: \(\frac{\pi}{6}\) radian = \(\frac{180^{\circ}}{6}\) = 30°

∴ The correct answer is 30°

Class 10 Maths Trigonometry Chapter 1 MCQs

Example 3. The circular value of each internal angle of a regular hexagon is

1. \(\frac{\pi}{3}\)
2. \(\frac{2\pi}{3}\)
3. \(\frac{\pi}{6}\)
4. \(\frac{\pi}{4}\)

Solution: The value of each internal angle of a regular hexagon is

⇒ \(\frac{2 \times 6-4}{6} \times 90^{\circ}=120^{\circ}\)

⇒ \( 180^{\circ}=\pi^c\)

⇒ \(120^{\circ}=\frac{120}{180} \pi^c=\frac{2 \pi^c}{3}\)

∴ The circular value of each angle is \(\frac{2 \pi^c}{3}\)

∴ The correct answer is 2. \(\frac{2\pi}{3}\)

Example 4. The measurement of θ in the relation to S = rθ is determined by

1. Sexagesimal system
2. Circular system
3. Those two methods
4. None of these

Solution: The correct answer is 2. Circular system

Trigonometric Ratios Mcqs Class 10

Example 5. In cyclic quadrilateral ABCD, if ∠A = 120°, then the circular value of ∠C is

1. \(\frac{\pi}{3}\)
2. \(\frac{\pi}{6}\)
3. \(\frac{\pi}{2}\)
4. \(\frac{2\pi}{3}\)

Solution: In cyclic quadrilateral ABCD, [The opposite angles of a cyclic quadrilateral are supplementary]

∠A + ∠C = 180°

120° + ∠C = 180°

⇒ ∠C = 60°

180° = π^c

∴ 60°= \(\frac{60}{180} \pi^c=\frac{\pi^c}{3}\)

∴ The correct answer is 1. \(\frac{\pi}{3}\)

Class 10 Trigonometry Chapter 1 Mcqs With Answers

Example 6. In ΔABC, point of intersection of ∠B and ∠C is O; if ∠BAC = 40°, then the circular value of ∠BOC is

1. \(\frac{5 \pi}{18}\)
2. \(\frac{4 \pi}{12}\)
3. \(\frac{11 \pi}{18}\)
4. \(\frac{2 \pi}{5}\)

Solution:

∠BOC = 90° + \(\frac{1}{2}\) ∠BAC

= 90° + \(\frac{1}{2}\) x 40° = 110°

180° = π^c

⇒ 110° = \(\frac{110}{180} \pi^c=\frac{11 \pi^c}{18}\)

∴ The correct answer is 3. \(\frac{11 \pi}{18}\)

Example 7. If ∠A + ∠B = \(\frac{5 \pi}{12}\) and ∠A – ∠B = 15° then the sexagesimal value of ∠B is

1. 45°
2. 60°
3. 75°
4. 30°

Solution:

⇒ ∠B = 30°

∴ The correct answer is 4. 30°

Trigonometric Identities Mcqs Class 10

Example 8. If O is the circumcentre of the ΔABC and ∠BOC = 120° then the circular value of ∠BAC is

1. \(\frac{\pi}{3}\)
2. \(\frac{\pi}{6}\)
3. \(\frac{2\pi}{3}\)
4. None of these

Solution:

∠BOC = 2 ∠BAC

⇒ ∠BAC = \(\frac{1}{2}\) ∠BOC = \(\frac{1}{2}\) x 120° = 60°

180 = π^c

60° = \(\frac{60}{180} \pi^c=\frac{\pi^c}{3}\)

∴ The correct answer is 1. \(\frac{\pi}{3}\)

WBBSE Class 10 Maths Geometry Chapter 1 Theorems Related To Circle Multiple Choice Questions

Example 1. The length of two chords of a circle with centre O are equal. If ∠AOB = 60°, then the value of ∠COD is

1. 40°
2. 30°
3. 60°
4. 90°

Solution:

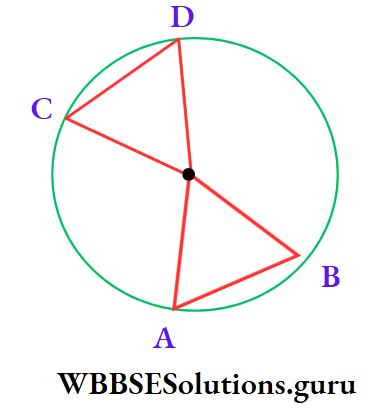
⇒ In a circle with its centre O,

⇒ Chord AB = Chord CD

∴ ∠AOB = ∠COD

Read And Learn Also WBBSE Class 10 Maths Multiple Choice Questions

∴ 60° = ∠COD

∴ The correct answer is 3. 60°.

Example 2. The length of a radius of a circle is 13 cm. and the length of a chord of a circle is 10 cm, the distance of the chord from the centre of the circle is

1. 12.5 cm
2. 12 cm
3. √69 cm
4. 24 cm

Solution:

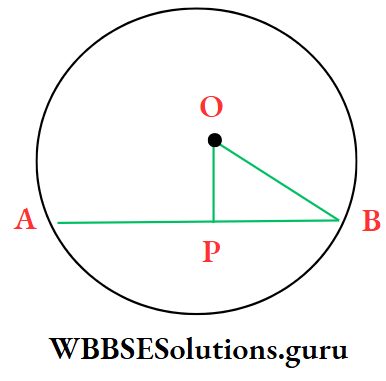
⇒ In a circle with its centre O, OP is the perpendicular distance of the chord AB.

⇒ join O, B.

⇒ OB = 13 cm ; AB = 10 cm

∵ OP ⊥ AB

∴ BP = \(\frac{1}{2}\) AB =\(\frac{1}{2}\) x 10 cm = 5 cm

⇒ In ΔBOP, OP² + BP² = OB² [From Pythagoras theorem)

⇒ OP² + 5² = 13²

⇒ OP = \(\sqrt{169-25}\) = √144 cm = 12 cm

∴ The correct answer is 2. 12 cm

Class 10 Maths Geometry Chapter 1 Mcqs 

Example 3. AB and CD are two equal chords of a circle with its centre O. If the distance of the chord AB from the point O is 4 cm. then the distance of the chord from the centre O of the circle

1. 2 cm
2. 4 cm
3. 6 cm
4. 8 cm

Solution:

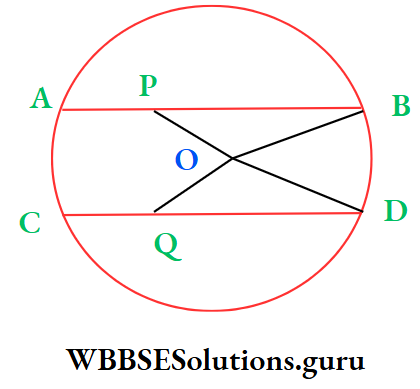
⇒ From the point O, two perpendiculars OP and OQ are drawn on the chord AB and CD respectively which intersect AB at the point P and CD at the point Q.

⇒ OP = 4 cm

⇒ Join O, B and O, D and OP ⊥ AB and OQ ⊥ CD

∴ BP = \(\frac{1}{2}\) AB and DQ = \(\frac{1}{2}\) CD

⇒ Again AB = CD [given]

⇒ \(\frac{1}{2}\) AB = \(\frac{1}{2}\) CD

∴ BP = DQ

⇒ From ΔBOP, ∠BPO = 90°

∴ OP² + BP² = OB²

⇒ 4² + BP² = OB² [From Pythagoras theorem]

⇒ 16 + BP² = OB²

⇒ In ΔDOQ, ∠OQD = 90°

∴ OQ² + DQ² = OD²

⇒ OQ²+ BP² = OD² [∵ BP = DQ]

⇒ As OB = OD [radii of same circle]

⇒ or, OB² = OD²

⇒ 16 + BP² = OQ² + BP²

⇒ OQ² = 16 cm²

⇒ OQ = √16 cm = 4 cm

∴ The correct answer is 2. 4 cm

Example 4. The length of each of two parallel chords is 16 cm. If the length of the radius of the circle is 10 cm, then the distance between two chord is

1. 12 cm
2. 16 cm
3. 20 cm
4. 5 cm

Solution:

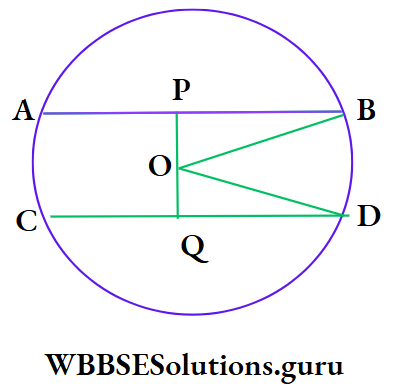
⇒  In the circle with its centre O, chord AB = chord CD = 16 cm and AB || CD ;

⇒  OP ⊥ AB and OQ ⊥ CD

∴ PB = \(\frac{1}{2}\) AB = \(\frac{1}{2}\) x 16 cm = 8 cm

⇒  DQ = \(\frac{1}{2}\) CD = \(\frac{1}{2}\) x 16 cm = 8 cm

From ΔBOP, OP² + PB² = OB²

⇒  OP² + 8² = 10² [OB is the radius of the circle]

⇒  OP = \(\sqrt{100-64}\) cm = 6 cm

Similarly, OQ = 6 cm

⇒ PQ = OP + OQ = (6 + 6) cm = 12 cm

∴ The correct answer is 1. 12 cm

Basic Geometry Mcqs Class 10

Example 5. The centre of two concentric circle is O; a straight line intersects a circle at the points A and B and another circle at the points C and D. If AC = 5 cm, then the length of BD is

1. 2.5 cm
2. 5 cm
3. 10 cm
4. none of these

Solution:

The centre of two concentric circle is O; a straight line intersects a circle at the points A and B and another circle at the points C and D.

From the point O a perpendicular OP is drawn on AB which intersects AB at the point P.

As OP ⊥ AB

∴ AP = BP

Again OP ⊥ CD  ∴ CP = DP

⇒ BP- DP = AP – CP

⇒ or, BD = AC = 5 cm

∴ The correct answer is 2. 5 cm

Example 6. If ‘O’ is the centre of circle and PQ is a diameter then the value of X is

1. 140
2. 40
3. 80
4. 20

Solution:

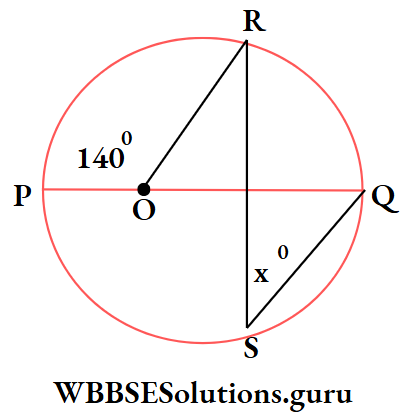
∠QOR = 180° – ∠POR = 180° – 40° = 40°

⇒ since the angle ∠QOR is at the centre of the circle and ∠QSR is on, the circle formed by circular arc QR of a circle with centre.

∴ 2∠QSR = ∠QOR

2x° = 40° or, x° = 20°

∴The correct answer is 4. 20.

Class 10 Geometry Chapter 1 Mcqs With Answers

Example 7. O is the centre of circle, ∠QPR = x°, ∠POR = 80° and ∠POQ = 140°, then the value of x is

1. 70
2. 60
3. 100
4. 80

Solution:

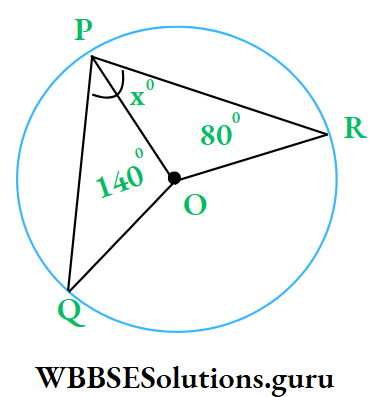
⇒ ∠QOR = 360° – ∠POQ – ∠POR

= 360° – 140° – 80° = 140°

⇒ ∠QPR = \(\frac{1}{2}\) ∠QOR

⇒ x° = \(\frac{1}{2}\) x 140°

⇒ x° = 70°

∴ The correct answer is 1. 70.

Example 8. O is the centre of circle, and BC is the diameter then the value of x is

1. 60
2. 50
3. 100
4. 80

Solution:

⇒ In ΔAOB, OA = OB [radii of same circle]

∴ ∠OBA = ∠OAB = 50°

⇒ i.e. ∠ABC = 50°

⇒ ∠ADC = ∠ABC [angles in the same segment]

⇒ x° = 50°

∴ The correct answer is 2. 50

Class 10 Maths Chapter 1 Geometry Solutions

Example 9. O is the circumcentre of ΔABC and ∠OAB = 50°, then the value of ∠ACB is

1. 50°
2. 100°
3. 40°
4. 80°

Solution:

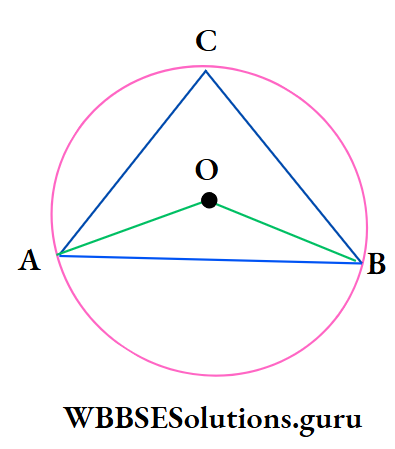
⇒ O is the circumcentre of ∠ABC

⇒ OA = OB [radii of same circle]

∴ ∠OBA = ∠OAB = 50°

⇒ ∠AOB = 180° – ∠OAB – ∠OBA

= 180° – 50° – 50° = 80° .

⇒ ∠ACB = \(\frac{1}{2}\) ∠AOB

= \(\frac{1}{2}\) x 80° = 40°.

∴ The correct answer is 3. 40°

Example 10. If O is centre of circle, the value of ∠POR is

1. 20°
2. 40°
3. 60°
4. 80°

Solution:

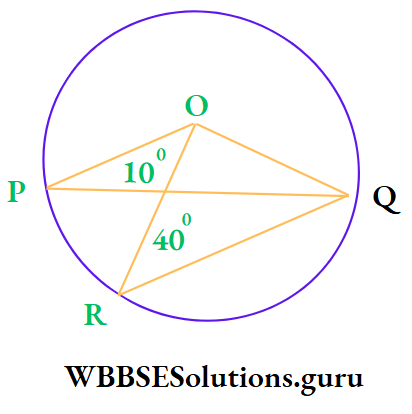
⇒ In ΔPOQ, OP = OQ [radii of same circle]

∴ ∠OQP = ∠OPQ = 10°

⇒ In ΔQOR, OR = OQ

∴ ∠OQR = ∠ORQ = 40°

∴ ∠PQR = ∠OQR – ∠OQP = 40° – 10° = 30°

⇒ ∠POR = ∠PQR = 2 x 30° = 60°

∴ The correct answer is 3. 60°

Example 11. O is the centre of the circle, if ∠ACB = 30°, ∠ABC = 60°, ∠DAB = 35° and ∠DBC = x°, the value, of x is

1. 35
2. 70
3. 65
4. 55

Solution:

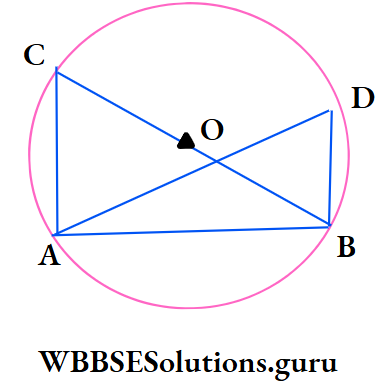
⇒ In ΔABC, ∠BAC = 180° – (∠ACB + ∠ABC)

= 180° – (30° + 60°) = 90°

⇒ ∠DAB = 35°

⇒ ∠CAD = 90° – ∠DAB = 90° – 35° = 55°

⇒ ∠DBC = ∠CAD = 55°

∴ The correct answer is 4. 55°

Wbbse Class 10 Maths Geometry Notes 

Example 12. O is the centre of the circle, if ∠BAD = 65°, ∠BDC = 45°, then the value of ∠CBD is

1. 65°
2. 45°
3. 40°
4. 20°

Solution:

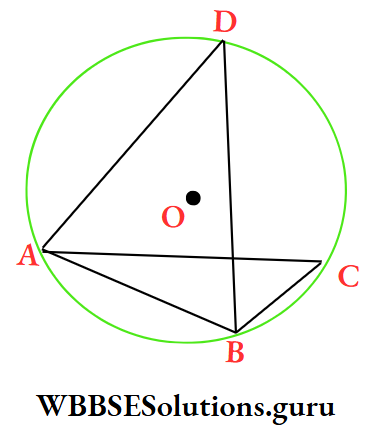
⇒ ∠BAC = ∠BDC [angles, in the same segment] = 45°

⇒ ∠CAD = ∠BAD – ∠BAC = 65° – 45° = 20°

⇒ ∠CBD = ∠CAD [angles in the same segment] = 20°

∴ The correct answer is 4. 20°

Example 13. The O is the centre of circle, if ∠AEB = 110° and ∠CBE = 30°, the value of ∠ADB is

1. 70°
2. 60°
3. 80°
4. 90°

Solution:

In ΔBEC,

⇒ Exterior ∠AEB = ∠ECB + ∠CBE

⇒ 110° = ∠ECB + 30°

⇒ or, ∠ECB = 110° – 30° = 80°

⇒ i.e. ∠ACB = 80°

⇒ ∠ADB = ∠ACB [angles in the same segment] = 80°

∴ The correct answer is 3. 80°.

Example 14. O is the centre of the circle, if ∠BCD = 28°, ∠AEC = 38°, then the value of ∠AXB is

1. 56°
2. 86°
3. 38°
4. 28°

Solution:

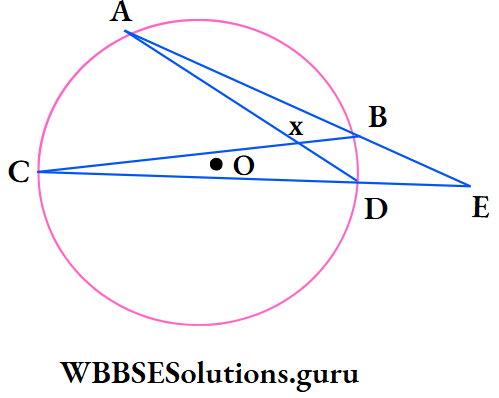
⇒ ∠BAD = ∠BCD [angles in the same segment] = 28°

⇒ In ΔADE, Exterior ∠ADC = ∠BAD + ∠AED

= 28° + 38° = 66°

⇒ In ΔCDX, ∠CXD = 180° – ∠XCD – ∠XDC

= 180° – 28° – 66° = 86°

∴ The correct answer is 2. 86°.

Geometry Mcqs With Solutions Class 10 

Example 15. O is the centre of the circle and AB is diameter. If AB || CD, ∠ABC = 25°, the value of ∠CED is

1. 80°
2. 50°
3. 25°
4. 40°

Solution:

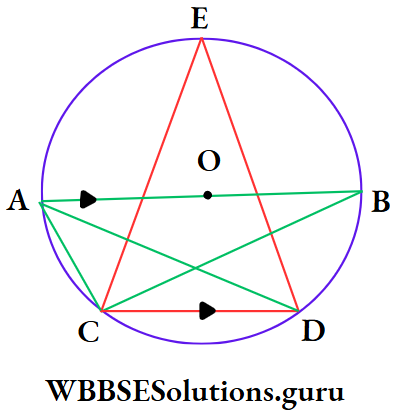
⇒ Join A, C and A, D

⇒ ∠ACB = 90° [semi-circular angle]

⇒ AB || CD and BC is intersection

⇒ ∠BCD = alternate ∠ABC = 25°

⇒ ∠ACD = ∠ACB + ∠BCD

= 90° + 25° = 115°

⇒ ∠ADC = ∠ABC [angles in the same segment]

= 25°

⇒ In ΔACD, ∠CAD = 180° – ∠ACD – ∠ADC

= 180° – 115° – 25° = 40°

⇒ ∠CED = ∠CAD [angles in the same segment]

∴ The correct answer is 4. 40°

Example 16. PQ is a diameter of a circle with centre O, and PR = RQ the value of ∠RPQ is

1. 30°
2. 90°
3. 60°
4. 45°

Solution:

⇒ ∠PRQ = 90° [semi-circular angle]

⇒ In ΔPQR, PR = RQ

∴ ∠RPQ = ∠PQR = \(\frac{180^{\circ}-90^{\circ}}{2}\) = 45°

∴ The correct answer is 4. 45°.

Example 17. QR is a cord of a circle and POR is a diameter of a circle. OD is perpendicular on QR. If OD = 4 cm, the length of PQ is

1. 4 cm
2. 2 cm
3. 8 cm
4. none of these

Solution:

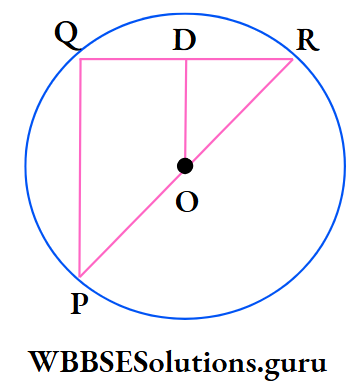
⇒ ∠PQR = 90°

⇒ ∠ODR = 90° [∵ OD ⊥ QR]

∴ ∠PQR = ∠ODR

∴ OD || PQ

∴ ΔPQR ~ ΔDOR

∴ \(\frac{\mathrm{OD}}{\mathrm{PQ}}=\frac{\mathrm{OR}}{\mathrm{PR}}\)

∴ PQ = 8 cm

∴ The correct answer is 3. 8 cm

Geometry Mcqs With Solutions Class 10 

Example 18. AOB is a diameter of a circle. The two chords AC and BD when entended meet at point E. If ∠COD = 40°, the value of ∠CED is

1. 40°
2. 80°
3. 20°
4. 70°

Solution:

I join A, D and B, C

⇒ since ∠COD is at the centre of the circle and ∠CAD is on the circle formed by circular arc CD of a circle with centre,

⇒ ∠CAD = \(\frac{1}{2}\) ∠COD

= \(\frac{1}{2}\) x 40° = 20°

⇒ ∠ADB = 90° [semi-circular angle]

∴ ∠ADE = 180° – 90° = 90°

⇒ In ΔADE, ∠AED = 180° – ∠ADE – ∠CAD

= 180° – 90° – 20° = 70°

i.e. ∠CED = 70°

∴The correct answer is 4. 70°.

Example 19. ADB is diameter of a circle. If AC = 3 cm, BC = 4 cm, then the length of AB is

1. 3 cm
2. 4 cm
3. 5 cm
4. 8 cm

Solution:

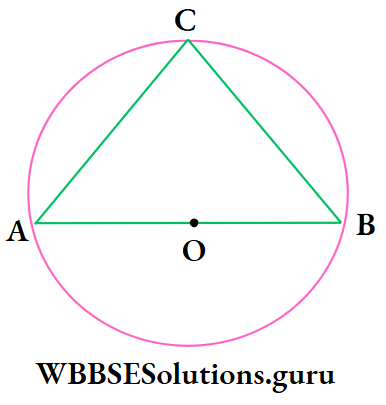
⇒ In ΔABC, ∠ACB = 90° [semi circular angle]

⇒ AB² = AC² + BC² [From Pythagoras theorem]

= (3² + 4²) cm² = 25 cm²

⇒ AB = √25 = 5 cm

∴ The correct answer is 3. 5 cm

Example 20. O is the centre of circle and AB is a diameter, if ∠BCE = 20°, ∠CAE = 25°, the value of ∠AEC is

1. 50°
2. 90°
3. 45°
4. 20°

Solution:

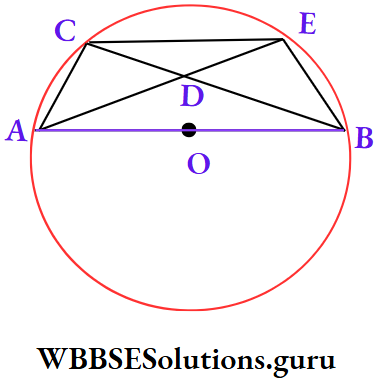
⇒ ∠ACB = 90° [semi circular angle]

⇒ ∠BCE = 20°

⇒ ∠ACE = ∠ACB + ∠BCE

= 90° + 20° = 110°

⇒ In ∠ACE, ∠AEC = 180° – ∠ACE – ∠CAE

= 180° – 110° – 25° = 45°

⇒ ∴ The correct answer is 3. 45°

Example 21. In the picture beside O is the centre of circle and AB is a diameter. ABCD is a cyclic quadrilateral. If ∠ADC = 120°, then the value of ∠BAC is

1. 50°
2. 60°
3. 30°
4. 40°

Solution:

ABCD is quadrilateral

∴ ∠ABC + ∠ADC = 180° [The opposite angles of a cyclic quadrilateral are supplementary]

⇒ ∠ABC + 120° =180°

⇒ ∠ABC = 60°

⇒ ∠ACB = 90° [semi-circular angles]

⇒ ∠BAC = 180° – 90° – 60° = 30°

∴ The correct answer is 3. 30°

Example 22. In picture beside O is the centre of circle and AB is a diameter. ABCD is a cyclic quadrilateral. If ∠ABC = 65°, ∠DAC = 60° then the value of ∠BCD is

1. 75°
2. 105°
3. 115°
4. 80°

Solution:

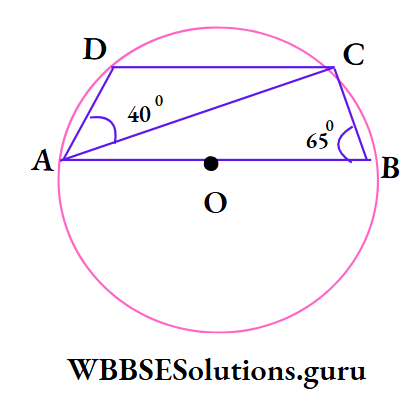
In ΔABC, ∠ACB = 90° [semi circular angle]

∠ABC = 65°

∴ ∠BAC = 180° – 65° – 90° = 25°

∴ ∠BAD = ∠BAC + ∠DAC

= 25° + 40° = 65°

⇒ ABCD is cyclic quadrilateral

∴ ∠BCD + ∠BAD = 180°, ∠BCD + 65° = 180°, ∠BCD = 115°

∴ The correct answer is 3. 115°

Class 10 Maths Important Mcqs For Board Exam 

Example 23. In picture beside O is the centre of circle and AB is diameter. ABCD is a cyclic quadrilateral in which AB || DC and if ∠BAC = 25° then the value of ∠DAC is

1. 50°
2. 25°
3. 130°
4. 40°

Solution:

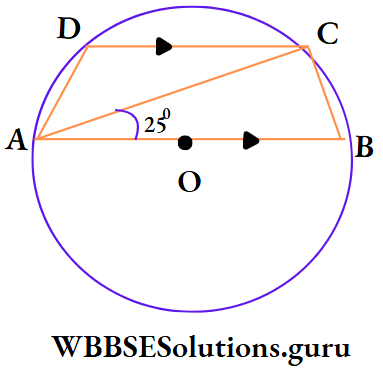
⇒ DC || AB and AC is the intersection

∴ ∠ACD = ∠BAC [alternate angle]

= 25°

⇒ ∠ACB = 90° [semi-circular angle]

∠BCD = ∠ACD + ∠ACB

= 25° + 90° = 115°

⇒ ABCD is cyclic quadrilateral

∴ ∠BAD + ∠BCD = 180°

⇒ ∠BAD + 115° = 180°

⇒ ∠BAD = 65°

⇒ ∠DAC = ∠BAD – ∠BAC

= 65° – 25° = 40°

∴ The correct answer is 4. 40°.

Example 24. In picture beside ABCD is a cyclic quadrilateral. BA is produced to the point F. If AE || CD, ∠ABC = 92° and ∠FAE = 20°, then the value of ∠BCD is

1. 20°
2. 88°
3. 108°
4. 72°

Solution:

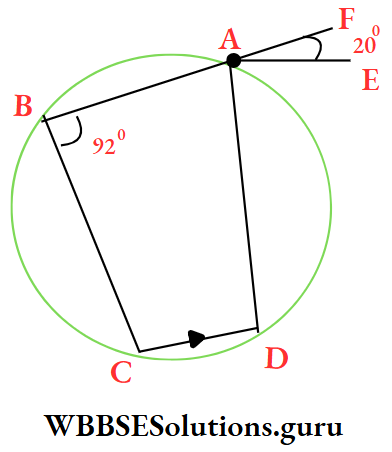
ABCD is a cyclic quadrilateral

∴ ∠ADC + ∠ABC = 180°

⇒ ∠ADC + 92° = 180°

⇒ or, ∠ADC = 88°

⇒ AE || DC and AD is the intersection

∴ ∠EAD = ∠ADC [alternate angle]

= 88°

⇒ ∠FAD = ∠EAD + ∠EAF

= 88° + 20° = 108°

⇒ For cyclic quadrilateral ABCD, exterior ∠FAD = interior opposite ∠BCD

∴ ∠BCD = 108°

∴ The correct answer is 3. 108°

Class 10 Maths Important Mcqs For Board Exam 

Example 25. In picture beside two circles intersect each other at the points C and D. Two straight lines through A the point D and C intersect one circles at the points E and F respectively. If ∠DAB = 75°, then the value of DEF is

1. 75°
2. 70°
3. 60°
4. 105°

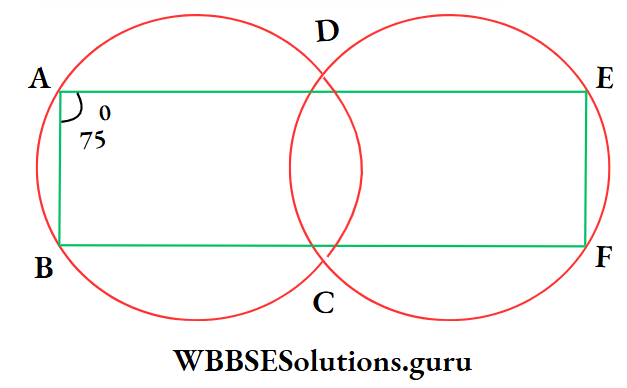
Solution:

I join D, C;

⇒ For cyclic quadrilateral ABCD, exterior ∠DCF = interior opposite ∠BAD = 75°

⇒ CDEF is a cyclic quadrilateral,

⇒ ∠DEF + ∠DCF = 180°

⇒ ∠DEF + 75° = 180°

⇒ ∠DEF = 175°

∴ The correct answer is 4. 105°

WBBSE Class 10 Maths Geometry Chapter 2 Theorems Related To Tangent Of A Circle Multiple Choice Questions

Example 1. A tangent drawn to a circle with centre O from an external point A touches the circle at the point B. If OB = 5 cm, AO = 13 cm, then the length of AB is

1. 12 cm
2. 13 cm
3. 6.5 cm
4. 6 cm

Solution:

⇒ OB is radius and AB is a tangent of a circle with centre O.

∴ OB ⊥ AB

⇒ On right angled triangle AOB, ∠AOB = 90°

∴ OB² + AB² = OA²

Read And Learn Also WBBSE Class 10 Maths Multiple Choice Questions

⇒ AB = \(\sqrt{\mathrm{OA}^2-\mathrm{OB}^2}\)

= \(\sqrt{13^2-5^2} \mathrm{~cm}\)

= √144 cm = 12 cm

∴ The correct answer is 1. 12 cm’

Example 2. Two circles touch each other externally at the point C. A direct common tangent AB touch the two circles at the points A and B. Value of ∠ACB is

1. 60°
2. 45°
3. 30°
4. 90°

Solution: Tangent drawn at the point C intersects AB at the point M.

⇒ MA and MC are two tangent from the point M to a circle with P.

∴ MA = MC

⇒ Similarly, MB = MC

⇒ In ΔAMC, MA = MC

∴ ∠MCA = ∠MAC

⇒ In ΔBMC, MB = MC

⇒ ∠MCB – ∠MBC

∴ ∠MCA + ∠MCB = ∠MAC + ∠MBC

⇒ i.e. ∠ACB = ∠BAC + ∠ABC

⇒ In ΔABC, ∠ACB + ∠BAC + ∠ABC = 180°

⇒ ∠ACB + ∠ACB = 180°

⇒ 2 ∠ACB = 180°

⇒ ∠ACB = 90°

∴ The correct answer is 4. 90°

Class 10 Maths Geometry Chapter 2 MCQs 

Example 3. The length of radius of a circle with centre O is 5 cm. P is a point at the distance of 13 cm from the point O. The length of two tangents are PO and PR from the point P. The area of quadrilateral PQRS is

1. 60 sq cm
2. 30 sq cm
3. 120 sq cm
4. 150 sq cm

Solution: PQ is a tangent and OQ is the radius of the circle with centre O,

∴ OQ ⊥ PQ

∴ ∠OQP = 90°

⇒ Similarly, ∠ORP 90°

⇒ OQ = OR = 5 cm and OP = 13 cm

⇒ In right-angled ΔPOQ, OQ² + PQ² = OP²

⇒ PQ² = OP² – OQ²

⇒ PQ = \(\sqrt{O P^2-O Q^2}\)

= \(\sqrt{13^2-5^2} \mathrm{~cm}\)

= √144 cm = 12 cm

⇒ PQ and PR are tangents of a circle with centre O,

∴ PR = PQ = 12 cm

⇒ Area of ΔPOQ = \(\frac{1}{2}\) x PQ x OQ

= \(\left(\frac{1}{2} \times 12 \times 5\right)\) sq. cm = 30 sq. cm

⇒ Similarly, ΔPOR = 30 sq. cm

∴ Area of quadrilateral PQOR = ΔPOQ + ΔPOR = (30 + 30) sq. cm = 60 sq. cm

∴ The correct answer is 1. 60 sq cm

Class 10 Geometry Chapter 2 Mcqs With Answers

Example 4. The lengths of radii of two circles are 5 cm and 3 cm. The two circles touch each other externally. The distance between two centres of two circles is

1. 2 cm
2. 2.5 cm
3. 15 cm
4. None of these

Solution: Two circles with centre A and B touch externally each other at point P.

⇒ AP = 5 cm, BP = 3 cm

⇒ AP and BP lies on the same straight line

∴ AB = AP + BP = (5 + 3) cm = 8 cm.

∴ The correct answer is 4. None of these

Wbbse Class 10 Maths Geometry Notes

Example 5. The lengths of radii of two circles are 3.5 cm and 2 cm. The two circles touch each other internally. The distance between the centres of two circles is

1. 5.5 cm
2. 1 cm
3. 15 cm
4. None of these

Solution: Two circles with centres A and B touch internally each other at point C.

⇒ Let BC = 3.5 cm, AC = 2 cm

∴ BC and AC lies on the same straight line

⇒ AB = BC – AC = (3.5 – 2) cm = 1.5 cm

∴ The correct answer is 3. 1.5 cm

WBBSE Class 10 Maths Geometry Chapter 3 Similarity Multiple Choice Questions

Example 1. A line parallel to the side BC of ΔABC intersects the sides AB and AC at points X and Y respectively. If AX = 2.4 cm, AY = 3.2 cm and YC = 4.8 cm, then the length of AB is

1. 3.6 cm
2. 6 cm
3. 6.4 cm
4. 7.2 cm

Solution:

In ΔABC, XY || BC

∴ \(\frac{\mathrm{AX}}{\mathrm{XB}}=\frac{\mathrm{AY}}{\mathrm{YC}}\) [by Thales thorem]

Read And Learn Also WBBSE Class 10 Maths Multiple Choice Questions

⇒ \(\frac{2 \cdot 4 \mathrm{~cm}}{\mathrm{XB}}=\frac{3 \cdot 2 \mathrm{~cm}}{4 \cdot 8 \mathrm{~cm}}\)

⇒ \(\mathrm{XB}=\frac{2 \cdot 4 \times 4 \cdot 8}{3 \cdot 2} \mathrm{~cm}\) = 3.6 cm

AB = AX + XB = (2.4 + 3.6) cm = 6 cm

∴ The correct answer is 2. 6 cm

Example 2. The point D and E are situated on the sides AB and AC of ΔABC in such a way that DE || BC and AD: DB = 3: 1; if EA = 3.3 cm, then the length of AC is

1. 11 cm
2. 4 cm
3. 4.4 cm
4. 5.5 cm

Solution:

In ΔABC, DE || BC

∴ \(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\)

⇒ \(\frac{3}{1}=\frac{3 \cdot 3 \cdot \mathrm{cm}}{\mathrm{EC}}\)

⇒ \(\mathrm{EC}=\frac{3 \cdot 3}{3} \mathrm{~cm}=1 \cdot 1 \mathrm{~cm}\)

AC = AE + EC = (3.3 + 1.1) cm = 4.4 cm

∴ The correct answer is 3. 4.4 cm

Class 10 Maths Geometry Chapter 3 MCQs

Example 3. If DE || BC, then the value of x is

1. 4
2. 1
3. 3
4. 2

Solution:

DE || BC

∴ \(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\)

⇒ \(\frac{x+3}{3 x+19}=\frac{x}{3 x+4}\)

⇒ (x + 3) (3x + 4) = x (3x + 19)

⇒  3x² + 13x + 12 = 3x² + 19x

⇒ x = 2

∴ The correct answer is 4. 2

Example 4. In the trapezium ΔBCD, AB || DC and the two points are situated on the sides AD and BC in such a way that PQ || DC; if PD = 18 cm, BQ = 35 cm, QC = 15 cm, then the length of AD is

1. 60 cm
2. 30 cm
3. 12 cm
4. 15 cm

Solution:

Let AB < DC; DA and CB are extended.

The extended side of DA and CB meet at O.

Let, AP = x cm. [x > 0]

As AB || DC and PQ || DC ∴ AB || PQ || DC

In ΔPOQ, AB || PQ

∴ \(\frac{\mathrm{OA}}{\mathrm{AP}}=\frac{\mathrm{OB}}{\mathrm{BQ}}\)

⇒ \(\frac{\mathrm{OA}}{\mathrm{AP}}+1=\frac{\mathrm{OB}}{\mathrm{BQ}}+1\)

⇒ \(\frac{\mathrm{OA}+\mathrm{AP}}{\mathrm{AP}}=\frac{\mathrm{OB}+\mathrm{BQ}}{\mathrm{BQ}}\)

i.e. \(\frac{\mathrm{OP}}{\mathrm{AP}}=\frac{\mathrm{OQ}}{\mathrm{BQ}}\)

⇒ \(\frac{\mathrm{OP}}{\mathrm{OQ}}=\frac{\mathrm{AP}}{\mathrm{BQ}}\)……..(1)

In ΔCOD, PQ || DC

∴ \(\frac{\mathrm{OP}}{\mathrm{PD}}\) = \(\frac{\mathrm{OQ}}{\mathrm{BQ}}\)

⇒ \(\frac{\mathrm{OP}}{\mathrm{OQ}}\) = \(\frac{\mathrm{PD}}{\mathrm{QC}}\)……(2)

From (1) and (2), \(\frac{\mathrm{AP}}{\mathrm{BQ}}\) = \(\frac{\mathrm{PD}}{\mathrm{QC}}\); \(\frac{x}{35}\) = \(\frac{18}{15}\)

⇒ x = \(\frac{18}{15}\) ⇒ x = 42

AD = AP + PD = (42 + 18) cm = 60 cm

∴ The correct answer is 1. 60cm

Class 10 Geometry Chapter 3 Mcqs With Answers

Example 5. If DP = 5 cm, DE = 15 cm, DQ = 6 cm and QF = 18 cm, then

1. PQ = EF
2. PQ || EF
3. PQ ≠ EF
4. PQ EF

Solution: DQ = 6 cm, QF = 18 cm

⇒ \(\frac{\mathrm{DQ}}{\mathrm{QF}}\) = \(\frac{6}{18}\) = \(\frac{1}{3}\)

PE = DE – DP = (15 – 5) cm = 10 cm

⇒ \(\frac{\mathrm{DP}}{\mathrm{PE}}\) = \(\frac{5}{10}\) = \(\frac{1}{2}\)

As, \(\frac{\mathrm{DP}}{\mathrm{QF}}\) ≠ \(\frac{\mathrm{DP}}{\mathrm{PE}}\)

So, PQ EF

∴ The correct answer is 4. PQ EF

Example 6. In ΔDEF and ΔPQR, if ∠D = ∠Q and ∠R = ∠E, then let us write which of the following is not right

1. \(\frac{\mathrm{EF}}{\mathrm{PR}}\) = \(\frac{\mathrm{DF}}{\mathrm{PQ}}\)
2. \(\frac{\mathrm{QR}}{\mathrm{PQ}}\) = \(\frac{\mathrm{EF}}{\mathrm{DF}}\)
3. \(\frac{\mathrm{DE}}{\mathrm{QR}}\) = \(\frac{\mathrm{DF}}{\mathrm{PQ}}\)
4. \(\frac{\mathrm{EF}}{\mathrm{RP}}\) = \(\frac{\mathrm{DE}}{\mathrm{QR}}\)

Solution: In ΔDEF and ΔPQR, ∠D = ∠Q, ∠R = ∠E

∴ 180° – (∠D + ∠E) = 180° – (∠Q + ∠R)

∴ ∠F = ∠P

∴ ΔDEF ~ ΔPQR

∴ \(\frac{\mathrm{DE}}{\mathrm{QR}}\) = \(\frac{\mathrm{EF}}{\mathrm{RP}}\) = \(\frac{\mathrm{DF}}{\mathrm{PQ}}\)

∴ The correct answer is 2. \(\frac{\mathrm{QR}}{\mathrm{PQ}}\) = \(\frac{\mathrm{EF}}{\mathrm{DF}}\)

Class 10 Maths Chapter 3 Geometry Solutions 

Example 7. In ΔABC and ΔDEF, if \(\frac{\mathrm{AD}}{\mathrm{DE}}\) = \(\frac{\mathrm{BC}}{\mathrm{FD}}\) = \(\frac{\mathrm{AC}}{\mathrm{EF}}\) then

1. ∠B = ∠E
2. ∠A = ∠D
3. ∠B = ∠D
4. ∠A = ∠F

Solution:

In ΔABC and ΔDEF, \(\frac{\mathrm{AD}}{\mathrm{DE}}\) = \(\frac{\mathrm{BC}}{\mathrm{FD}}\) = \(\frac{\mathrm{AC}}{\mathrm{EF}}\)

∴ ΔABC ~ ΔDEF

∴ ∠A = ∠E ; ∠B = ∠D and ∠C = ∠F

∴ The correct answer is 3. ∠B = ∠D

Example 8. In ΔABC and ΔDEF, if ∠A = ∠E = 40°, AB : ED = AC : EF and ∠F = 65°, then the value of ∠B is

1. 35°
2. 65°
3. 75°
4. 85°

Solution:

In ΔDEF, ∠D = 180° – (∠E + ∠F)

= 180° – (40° + 65°) = 75°

In ΔABC and ΔDEF, ∠A = ∠E = 40° and \(\frac{\mathrm{AB}}{\mathrm{ED}}\) = \(\frac{\mathrm{AC}}{\mathrm{EF}}\)

∴ ΔABC ∼ ΔDEF  ∴ ∠B = ∠D = 75°

∴ The correct answer is 3. 75°

Wbbse Class 10 Maths Geometry Notes 

Example 9. In ΔABC and ΔPQR, if \(\frac{\mathrm{AB}}{\mathrm{QR}}\) = \(\frac{\mathrm{BC}}{\mathrm{PR}}\) = \(\frac{\mathrm{CA}}{\mathrm{PQ}}\) then

1. ∠A = ∠Q
2. ∠A = ∠P
3. ∠A = ∠R
4. ∠B = ∠Q

Solution:

ΔABC and ΔPQR, \(\frac{\mathrm{AB}}{\mathrm{QR}}\) = \(\frac{\mathrm{BC}}{\mathrm{PR}}\) = \(\frac{\mathrm{CA}}{\mathrm{PQ}}\)

∴ ΔABC ~ ΔPQR  ∴ ∠A = ∠Q

∴ The correct answer is 1. ∠A = ∠Q

Example 10. In ΔABC, AB = 9 cm, BC = 6 cm, CA = 7.5 cm. In ΔDEF the corresponding side of BC is EF; EF = 8 cm and if ΔDEF ~ ΔABC, then the perimeter of ΔDEF will be

1. 22.5 cm
2. 25 cm
3. 27 cm
4. 30 cm

Solution: ΔABC ~ ΔDEF and EF is a corresponding side of BC

∴ ∠A = ∠D, ∠B = ∠E and ∠C = ∠F

∴ \(\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{AC}}{\mathrm{DF}}=\frac{\mathrm{BC}}{\mathrm{EF}}=\frac{6}{8}=\frac{3}{4}\)

⇒ \(\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{3}{4}\)

⇒ \(\frac{9 \mathrm{~cm}}{\mathrm{DE}}=\frac{3}{4}\) or, DE = 12cm

⇒ \(\frac{\mathrm{AC}}{\mathrm{DF}}=\frac{3}{4}, \quad \frac{7 \cdot 5 \mathrm{~cm}}{\mathrm{DF}}=\frac{3}{4}\)

or, DF = 10 cm

∴ Perimeter of ΔDEF = (12 + 10 + 8) cm = 30 cm

∴ The correct answer is 4. 30 cm

WBBSE Class 10 Maths Geometry Chapter 4 Pythagoras Theorem Multiple Choice Questions

Example 1. A person goes 24 m. west from a place and then he goes 10 m. north. The distance of the person from starting point is

1. 34 m
2. 17 m
3. 26 m
4. 25 m

Solution: A person goes to position Q, 24 m. west from position P and then he goes to position R, 10 m north from Q; I join P, R.

∴ PQ = 24 m, QR = 10 m and ∠PQR = 90°

∴ In right-angled ΔPQR,

PR² = PQ² + QR² [By Pythagorus theorem]

Read And Learn Also WBBSE Class 10 Maths Multiple Choice Questions

⇒ PR = \(\sqrt{\mathrm{PQ}^2+\mathrm{QR}^2}\)

= \(\sqrt{(24)^2+(10)^2} \mathrm{~m}\)

= √676 m=26m

∴ The distance of the person from starting point is 26 m

∴ The correct answer is 3. 26 m

Example 2. If ABC is an equilateral triangle and AD ⊥ BC then AD² =?

1. \(\frac{3}{4}\)DC²
2. 2 DC²
3. 3 DC²
4. 4 DC²

Solution:

ΔABC is an equilateral triangle and AD ⊥ BC

∴ D is the midpoint of BC

∴ BC = 2DC

In right-angled ΔADC, AD² + DC² = AC²

AD² + DC² = BC²  ∵ [AC = BC]

AD² = (2DC)² – DC² = 4DC² – DC²

AD² = 3DC²

∴ The correct answer is 3. 3 DC²

Class 10 Maths Geometry Chapter 4 MCQs

Example 3. In an isosceles triangle ABC, if AC = BC and AB² = 2AC², then the measure of ∠C is

1. 30°
2. 90°
3. 45°
4. 60°

Solution: AB² = 2AC² = AC² + AC²

AB² = AC² + BC²  [∵ AC = BC]

∴ ΔABC is a right-angle triangle whose hypotenuse is AB.

∴ ∠C = 90°

∴ The correct answer is 2. 90°

Example 4. Two rods of 13 m. length and 7 m. length are situated perpendicularly on the ground and the distance between their foots is 8 m. The distance between their top. parts is

1. 9 m
2. 10 m
3. 11 m
4. 12 m

Solution: Let, the length of rod AB is 13 m and length of rod CD is 7 m.

Area Of Circles Mcqs With Solutions Class 10

The distance (BD) between them is 8 m let the distance (AC) between their top is x m. [x > 0]

I drawn CE ⊥ AB

AB ⊥ CD and CD ⊥ BD,  ∴ AB || CD  i.e., EB || CD

Again, CE ⊥ AB and DB ⊥ AB,  ∴ CE || DB

∴ BDCE is a parallelogram

∴ EB = CD = 7 m and EC = BD = 8 cm

AE = AB – EB = (13 – 7) m = 6 m.

In right-angled ΔAEC, ∠AEC = 90°

∴ AC² = AE² + EC² [By Pythagoras theorem]

x² = 6² + 8²

⇒ x = √100 = 10

∴ The distance between their top part is 10 m.

∴ The correct answer is 2. 10 m

Class 10 Maths Chapter 4 Geometry Solutions

Example 5. If the lengths of two diagonals of a rhombus are 24 cm and 10 cm. The perimeter of the rhombus is

1. 13 cm
2. 26 cm
3. 52 cm
4. 25 cm

Solution: Let the point of intersection of diagonals AC and BD of a rhombus ABCD is O ; AC = 24 cm, BD = 10 cm.

The diagonals of a rhombus are bisects each other perpendicularly.

∴ ∠AOB = ∠BOC = ∠COD = ∠DOA = 90°

OA = OC = \(\frac{1}{2}\) AC = \(\left(\frac{1}{2} \times 24\right)\) cm = 12 cm

OB = OD = \(\frac{1}{2}\) BD = \(\left(\frac{1}{2} \times 10\right)\) cm = 5 cm

In right angled ΔAOB, AB2 = OA² + OB²  [by Pythagoras theorem]

⇒ AB = \(\sqrt{\mathrm{OA}^2+\mathrm{OB}^2}\)

= \(\sqrt{12^2+5^2} \mathrm{~cm}\) = √169 cm = 13 cm

∴ Perimeter of rhombus is (13 x 4) cm or 52 cm

∴ The correct answer is 3. 52 cm

WBBSE Class 10 Maths Trigonometry Chapter 4 Application Of Trigonometric Ratios Height And Distance Multiple Choice Questions

Example 1. If the angle of elevation of the top of the mobile tower from a distance of 10 metres from its food is 60°, then the height of the tower is 

1. 10 m
2. 10√3 m
3. \(\frac{10}{\sqrt{3}}\) m
4. 100 m

Solution:

⇒ Let the height of tower (AB) = x m. and angle of elevation of the top of mobile tower is ∠ACB where ∠ACB = 60°

⇒ BC = 10 m

⇒ From ΔABC, ∠ABC = 90°

Read And Learn Also WBBSE Class 10 Maths Multiple Choice Questions

∴ \(\frac{AB}{BC}\) = tan 60°

\(\frac{x}{10}\) = √3

⇒ x = 10√3

∴ The height of the tower is 10√3 m

∴ The correct answer is 2. 10√3 m

Example 2. A value of θ is

1. 30°
2. 45°
3. 60°
4. 75°

Solution: ΔABC, ∠ABC = 90°

∴ \(\tan \theta=\frac{A B}{B C}=\frac{5}{5 \sqrt{3}}\)

⇒ \(\tan \theta=\frac{1}{\sqrt{3}}=\tan 30^{\circ}\)

∴ θ = 30°

∴ The correct answer is 1. 30°

Class 10 Maths Trigonometry Chapter 4 MCQs

Example 3. At what angle an observer observes a box lying on ground from the roof of three storied building, so that the height of the building is equal to the distance of the box from the building, then the angle is

1. 15°
2. 30°
3. 45°
4. 60°

Solution: Let height of building is AB and the distance of the box from the building is BC

∴ AB = BC

⇒ Let required angle is ∠ACB

⇒ From ΔABC, ∠ABC = 90°

⇒ tan ∠ACB = \(\frac{AB}{BC}\)

⇒ tan ∠ACB = \(\frac{AB}{AB}\) [as AB = BC]

⇒ tan ∠ACB = 1 = tan 45°, ∠ACB = 45°

∴ The correct answer is 3. 45°

Example 4. Height of tower is 100√3 metre. The angle of elevation of the top of a tower from a point at a distance of 100 metres of foot of tower is

1. 30°
2. 45°
3. 60°
4. None of these

Solution: Let height of tower is AB the angle of elevation of the top of a tower from a point C at a distance BC is θ

∴ AB = 100√3 metre and BC = 100 metre

⇒ In ΔABC, ∠ABC = 90°

∴ tanθ = \(\frac{A B}{B C}=\frac{100 \sqrt{3}}{100}=\sqrt{3}\)

⇒ tanθ = tan 60° ⇒ θ = 60°

∴ The correct answer is 3. 60°

Trigonometric Equations Mcqs Class 10

Example 5. If the length of shadow on the ground of a post is √3 times of its height, the angle of elevation of the sun is

1. 30°
2. 45°
3. 60°
4. none of these

Solution: Let, the length of post is AB and the length of shadow on the ground of the post is BC

∴ BC = √3 AB

Let the angle of elevation of the sun is θ

⇒ In ΔABC, ∠ABC = 90°

⇒ tanθ = \(\frac{A B}{B C}=\frac{A B}{\sqrt{3} A B}=\frac{1}{\sqrt{3}}\)

⇒ tanθ = tan 30°

⇒ θ = 30°

∴ The correct answer is 1. 30°

Example 6. If the angle of elevation of a light post of height 20 m is 45°, then the length of shadow of the post is

1. 20 m
2. 20√3 m
3. \(\frac{20}{\sqrt{3}} \mathrm{~m}\)
4. 10 m

Solution: The height of light post (AB) is 20 m and length of shadow of the post is BC;

∠ABC = 90°, ∠ACB = 45°

⇒ In ΔABC, \(\frac{AB}{BC}\) = tan 45°

⇒ \(\frac{20 M}{BC}\) = 1

⇒ BC = 20 m.

∴ The correct answer is 1. 20 m

Class 10 Maths Chapter 4 Trigonometry Solutions

Example 7. ∠ABD = 90°, AB = 10 m, the angle of elevation of point A at D and C are 45° and 30°, if DC = x m, then the value of x is

1. 10(√2 +1)
2. 10(√3+1)
3. 10(√3-1)
4. 10(√2 -1)

Solution: In ΔABD, \(\frac{AB}{BD}\) = tan 45°

⇒ \(\frac{10 M}{BD}\)

⇒ BD = 10 m

⇒ In ABC, \(\frac{AB}{BC}\) = tan 30°

⇒ \(\frac{10}{10+x}=\frac{1}{\sqrt{3}}\)

⇒ 10 + x= 10√3

⇒ x = 10(√3-1)

∴ The correct answer is 3.

WBBSE Class 10 Maths Trigonometry Notes

Example 8. If the ratio of the length of shadow of the tower and the height of the tower is 1: 1 then the angle of elevation of the sun is

1. 30°
2. 45°
3. 60°
4. 90°

Solution: AB is the height and BC is length of the shadow of tower AB.

⇒ AB : BC = 1 : 1

⇒ \(\frac{AB}{BC}\) = 1 ⇒ AB = BC

⇒ In ΔABC, ∠ABC = 90°

⇒ tan ∠ACB = \(\frac{AB}{BC}\) = \(\frac{AB}{AB}\) = 1

⇒ tan ∠ACB = tan 45°

⇒ ∠ACB = 45°

The angle of elevation is 45°

∴ The correct answer is 2. 45°

WBBSE Class 10 Maths Trigonometry Chapter 3 Trigonometric Ratios Of Complementary Multiple Choice Questions

Example 1. The value of (sin 43° cos 47° + cos 43° sin 47°) is

1. 0
2. 1
3. sin 4°
4. cos 4°

Solution: sin 43° cos 47° + cos 43° sin 47°

Read And Learn Also WBBSE Class 10 Maths Multiple Choice Questions

⇔ sin 43° cos (90° – 43°) + cos 43° sin (90° – 43°)

= sin 43° sin 43° + cos 43° cos 43°

= sin2 43° + cos2 43° – 1

∴ The correct answer is 2. 1

Example 2. The value of \(\left(\frac{\tan 35^{\circ}}{\cot 55^{\circ}}+\frac{\cot 78^{\circ}}{\tan 12^{\circ}}\right)\) is

1. 0
2. 1
3. 2
4. None of these

Solution: \(\frac{\tan 35^{\circ}}{\cot 55^{\circ}}+\frac{\cot 78^{\circ}}{\tan 12^{\circ}}\)

= \(\frac{\tan 35^{\circ}}{\cot \left(90^{\circ}-35^{\circ}\right)}+\frac{\cot 78^{\circ}}{\tan \left(90^{\circ}-78^{\circ}\right)}=\frac{\tan 35^{\circ}}{\tan 35^{\circ}}+\frac{\cot 78^{\circ}}{\cot 78^{\circ}}\)

= 1 + 1 = 2

∴ The correct answer is 3. 2

Class 10 Trigonometry Chapter 3 Mcqs With Answers

Example 3. The value of {cos (40° + θ) – sin (50° – θ)} is

1. 2 cosθ
2. 7 sinθ
3. 0
4. 1

Solution: cos (40° + θ) – sin (50° – θ)

= cos (40° +θ) – cos {90° – (50° – θ)) = cos (40° + θ) – cos (90° – 50° + θ)

= cos (40° + θ) – cos (40° + θ) = 0

∴ The correct answer is 3. 0

Example 4. ABC is a triangle, \(\sin \left(\frac{B+C}{2}\right)\) =

1. sin \(\frac{A}{2}\)
2. cos \(\frac{A}{2}\)
3. sin A
4. cos A

Solution: A + B + C = 180°

= \(\sin \left(90^{\circ}-\frac{A}{2}\right)=\cos \frac{A}{2}\)

∴ The correct answer is 2. cos \(\frac{A}{2}\)

Example 5. If A + B = 90° and tan A = \(\frac{3}{4}\), then the value of cot B is

1. \(\frac{3}{4}\)
2. \(\frac{4}{3}\)
3. \(\frac{3}{5}\)
4. \(\frac{4}{5}\)

Solution: tan A = \(\frac{3}{4}\)

⇒ tan (90° – B) = \(\frac{3}{4}\) [as A + B = 90°]

⇒ cot B = \(\frac{3}{4}\)

∴ The correct answer is 1. \(\frac{3}{4}\)

Class 10 Maths Chapter 3 Trigonometry Solutions 

Example 6. If tanθ tan 2θ = 1, and 20 is positive acute angle then the value of sin 3θ is

1. 0
2. 1
3. -1
4. 2

Solution: tanθ tan 2θ= 1

⇒ tan 2θ = \(\frac{1}{\tan \theta}\)

⇒ tan 2θ = cotθ

⇒ tan 2θ = tan (90° – θ)

⇒ 2θ = 90° – θ

⇒ 3θ = 90°

sin 3θ = sin 90° = 1

∴ The correct answer is 2. 1

Example 7. The value of \(\left(\frac{1}{\cos ^2 75^{\circ}}-\frac{1}{\tan ^2 15^{\circ}}\right)\) is

1. 1
2. 0
3. -1
4. 2

Solution: \(\left(\frac{1}{\cos ^2 75^{\circ}}-\frac{1}{\tan ^2 15^{\circ}}\right)\)

= sec²75° – cot²15°

= sec²75° – cot² (90° – 75°)

= sec²75° – tan²75° = 1

∴ The correct answer is 1. 1

Trigonometric Identities Mcqs With Solutions Class 10

Example 8. If α + β = 90°, then the value of \(\frac{\tan \alpha-\cot \beta}{\tan \alpha+\cot \beta}\) is

1. 3
2. 1
3. 0
4. \(\frac{1}{\sqrt{3}}\)

Solution: \(\frac{\tan \alpha-\cot \beta}{\tan \alpha+\cot \beta}=\frac{\tan \alpha-\cot \left(90^{\circ}-\alpha\right)}{\tan \alpha+\cot \left(90^{\circ}-\alpha\right)}\)

= \(\frac{\tan \alpha-\tan \alpha}{\tan \alpha+\tan \alpha}=0\)

∴ The correct answer is 3. 0