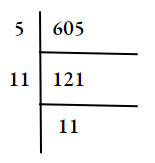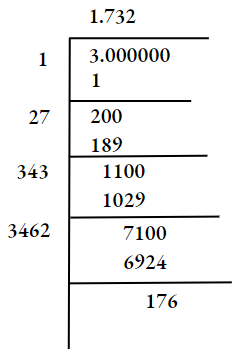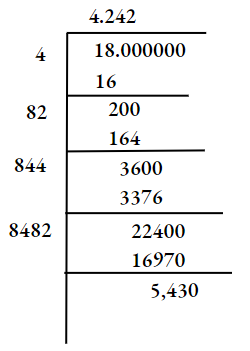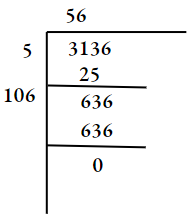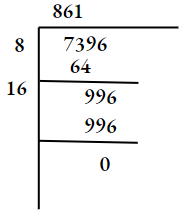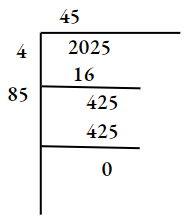Class 7 Maths

WBBSE Solutions For Class 7 Maths  Geometry Chapter 5 Concept Of Congruency

Question 1. what is congruency?
Solution:

Congruency is the property of two geometrical Figures if one of them can be made to coincide with the other by means of reflection, transformation, translation, or rotation of their combination.

If the two Geometrical Figures are of the same shape and size they are said to be congruent to each other.

In two triangles ABC and DEF, IF AB = DE, BC= EF, CA= DF

∠A = ∠A, ∠B = ∠E, ∠C = ∠F

∴ ΔABC ≅ ΔDEF

Question 2. Write the condition of the congruence of a triangle.
Solution:

Congruence of triangle

Two triangles are said to be congruent if their respective side angles are equal and when they are placed upon one another cover each other completely.

In two triangles ABC, DEF.

Condition:

IF AB=DE, BC= EF, CA= FD, and

∠A = ∠D, ∠B = ∠E, ∠C = ∠F

∴ ΔABC ≅ ΔDEF

Question 3. What is SSS congruency of a triangle? SSS (Side-Side – Side)
Solution:

If the lengths of three sides of a triangle are equal to the lengths of three sides of the other triangle then the triangles are congruent.

In ΔABC and ΔDEF

AB= DE, BC= EF and AC = DF

∴ ΔAB C ≅ ΔDEF

Question 4. what is the SAS congruency of a triangle SAS (Side- Angle- side)
Solution:

Two triangles are congruent if the length of two sides and the measurement of the included angle of one triangle are equal to the length of two sides and the measurement of the included angle of the other triangle

In ΔABC and ΔDEF

AB = DE, ∠ABC = ∠DEF and BC= EF

∴ ΔABC ≅ ΔDEF

Question 5. What is AAS congruency of a triangle AAS (Angle- Angle-side)
Solution:

Two triangles are congruent if the measurement of any Pair of angles and length of one pair of corresponding Sides are equal to other triangle.

In ΔABC and ΔDEF

∠B= ∠E, ∠C = ∠F and AB = DE

∴ ΔABC ≅ ΔDEF.

Question 6. What is RHS congruency of a triangle? RHS (Right Angle- Hypotenuse – Side)
Solution:

If in two right-angled triangles, the length of the hypotenuse and the length of one triangle is equal to the length of the hypotenuse and the length of one side of the other triangle, then the two triangles are congruent.

In ΔABC and ΔDEF

∠ABC ≈ ∠DEF = 90°

Hypotenuse AC = Hypotenuse DF and AB = DE

∴ ΔABC ≅ ΔDEF

Question 7. Find out whether the triangles are congruent
Solution:

AB = PQ, ∠A = ∠P

BC = QR, ∠B = ∠Q

CA = PR, ∠C = ∠R

Then the triangles are incongruent

Here,

AB ≠ PQ, ∠A = ∠P

BC = QR, ∠Q ≠ ∠B

CA ≠ PR, ∠C ≠ ∠R

∴ The triangles are non- congruent.

2.

Here,

AB ≠ DE

BC ≠ EF

CA ≠ DF

∴ The ΔABC and ΔDEF are not congruent.

3.

Let us Name the triangles First

BC = QR, ∠C = ∠R

∠B = ∠Q Sum of angles in a Δ^le is 180.

∠P = ∠A

According to the AAS Condition, the two triangles are in Congruence.

4.

In ΔABC and ΔDEF

∠ABC = ∠DEF = 90°

Hypotenuse AC = DF and AB = DE,

∴ ΔABC ≅ ΔDEF

5.

According to SSS Congruent

AB = DE

BC = EF

AC = FD

∴ ΔABC ≅ ΔDEF

6.

Let us Name the triangles First ΔABC, ΔDEF

Given the sides of Δ^le

AB ≠ DE

BC ≠ EF

AC ≠ FD

∴ The ΔABC and ΔDEF are non-congruent.

WBBSE Solutions For Class 7 Maths Geometry Chapter 8 Construction Of Quadrilateral

Question 1. Find the least number of data required to construct a

1. Parallelogram
2. Square
3. Rectangle and rhombus

Solution: 2. Square

Question 2. Draw a quadrilateral ABCD where AB=3.8cm, BC= 3cm, CD=4cm, AD= 2.5cm and ∠BAD=75°

Solution:

1. Draw a line AB with 3.8cm
2. Draw LBAD=75° and draw an Arc with 2.5cm. and on LBAD.
3. Draw an Arc with a radius of 3 cm from point B.
4. Draw an Arc with a radius of 4 cm from point D. where two Arcs meet Note the point as ‘c’
5. Now Join the line from B to C. and to D.
6. Now the Quadrilateral ABCD is formed.

Class 7 Geometry Chapter 8 Exercise Solutions

Question 3. Construct a quadrilateral PQRS in which PQ = 5.2cm, QR=3.5cm, RS= 4.6cm, SP = 3cm, and PR = 5.5cm
Solution:

1. Draw a line PR with a length of 5.5cm
2. Draw an arc with a radius of 5.2cm, from P. and draw an arc with a radius of 3.5cm from R on the above side of PR. Now mour the point as ‘Q’
3. Now Draw an arc 3cm from ‘p’ and Draw an arc with a radius of 4.6 cm
4. Now Join the mark the Joining of two arcs is Noted as ‘s’.
5. Now Join the pa and QR and also PS and RS.
6. After joining the PQ, QR, PS, and RS are formed quadrilateral PQRS.

Question 4. Construct a quadrilateral EFGH in which EH = 3.5cm, EF = 5cm, FG = 4.5 cm, ∠HEF = = 8.5° and ∠EFG =75°
Solution:

1. Draw a line EF with a length of 5 cm.
2. Make the ∠EFG = 75°, and draw aline with the angle of 75° and draw a Arc with 4.5cm From ‘F’ and make the point as ‘G’.
3. Make the ∠HEF = 85° and draw a line with the angle of 85° and draw an area with 3.5cm From E and make the point ‘H’.
4. Now Join the line ‘GH’.
5. Now the quadrilateral EFGH is formed.

WBBSE Solutions For Class 7 Maths Chapter 8 

Question 5. Construct a periodogram ABCD where AB = 4.6cm, BC = 7cm, and ∠ABC = 60°
Solution:

1. Draw a line BC with 7cm. and make the ∠ABC = 60°.
2. Draw a line through the angle ∠ABC = 60°, arc with 4.6cm, and make a point ‘A’.
3. Draw an Arc with a length of 7cm From ‘A’ and Draw another one 46cm From point ‘C’ and Joining of two Arcs marked as ‘D’.
4. Now Join the A to D and C to ‘D’
5. Now paraudogram ABCD is formed.

Question 6. Construct a rectangle PARS where pq=6cm and QR = 8cm
Solution:

1. Draw a line QR with a length of 8 cm.
2. We know that each angle in a rectangle is 90° so make 90° angle From Q and R.
3. Draw a line through the angle we know the opposite sides are equal in a rectangle.
4. Now Draw a sa arc witch 6cm from Q, on the 90° angle line as ‘p’
5. Now Draw an arc with 6cm from ‘R’ on the 90° angle line as ‘s’
6. Now Join the P, S
7. A rectangle PQRS is formed.

Class 7 Maths Chapter 8 Geometry PDF

Question 7. Construct a square in which the length of each side is 4.8cm.
Solution:

1. Draw a line with a length of 4.8 cm; Now Draw a semi-circle with a radius as you like from Both Sides of the line
2. Now Take the other radius make the area on the semicircle, From the Baseline and draw another arc from the first area point
3. Now Take another radius And draw anchorages from semicircle ABC which makes the 90°
4. Now Draw an area with a length of 4.8 cm
5. Repeat the process mentioned in points 2, and, 3,4.
6. Now Joining of two Arcs drawn on a 90°angle straight line.
7. Now the square is formed with a side of 4.8 cm.

Question 8. onstruct a rhombus ABCD in which AB = 5cm) and /B = 45°.
Solution:

1. Draw a line segment AB
2. Draw an arc from point ‘B’ and make are from the line Joining Arc to the and Draw an arc with a length 5 cm from the First and une Joining at the semicircle
3. Mask the point c and point A as shown.
4. Now Draw Draw a is from ‘A’ and ‘c’ with a length of 5cm
5. Now Join Points ‘A’ and ‘D’. and also C to ‘D’.
6. ∴ ABCD is a thrombus formed.

WBBSE Class 7 Maths Geometry Chapter 8

Question 9. Construct a square PQRS in which PR= 5.2cm.
Solution:

1. Draw a line PR with a length of 5.2cm
2. Draw a semi-circle with some radius from P and Q as shown
3. Now Draw a arcs on the semicircle from the point where the Semicircle and line Join Draw another arc on two semicircles.
4. Now Draw another area from the first area on the two semicircles
5. таке another radius and draw another two areas from the First and second are on the semicircles
6. Now draw a line through the Interaction of arcs From P and Ras shown.
7. Now draw an Arc with a radius 5.2cm and from pand R Now Join the two arcs
8. Now a square PQRS is formed.

Question 10. Construct a Rectangle ABCD in which AC = 4.5cm and ∠ACB=60°
Solution:

1. Draw a line ‘C’ from ‘A’
2. Now Draw an Arc from point ‘C’ and draw another arc from the line and joining of the Arc.
3. Now Draw the arc from C and line and name it as ‘A’
4. NOW Draw an arc From A and B. The point of intersection is ‘D’
5. Now Join the line A to D and B toD.
6. ∴ The rectangle ABCD is formed.

Geometry Chapter 9 Symmetry

Question 1. Choose the correct answer.

1. The number of lines of symmetry of a square

1. 1
2. 2
3. 3
4. 4

∴ The option(4) 4 is the correct answer.

2. The number of lines symmetry of a circle is

1. 2
2. 3
3. 4
4. Infinite

∴ The option (4) Infinite is the correct answer.

3. There is no centre of rotation of

1. Circle
2. Rhombus
3. Isosceles trapezium
4. Equilateral triangle

∴ The option (3) Isosceles trapezium is correct answer

Read and Learn More Class 7 Maths Solutions

4. In which Figure has no line of symmetry

1. H
2. P
3. T
4. X

∴ The option (2) P is the correct answer.

Class 7 Geometry Chapter 9 Exercise Solutions

5. In which Figure has a line of symmetry and rotational symmetry both?

1. Isosceles triangle.
2. Isosceles trapezium
3. Circle
4. Parallelogram.

∴ The option (3) Circle is the correct answer

Question 2. write true or False:

1. Isosceles triangle has no line of symmetry → True

2. The number of rotational symmetry of the circle is ‘2’ → False

3. The angle of rotation of the rectangle is 90°→ False

4. The order of rotational Symmetry of a square is 4. → True

5. The largest number of lines of symmetry of a triangle is 3 → True.

Class 7 Maths Chapter 9 Geometry PDF

Question 3. Fill in the blanks:-

1. Trapezium has no Line of symmetry or rotational Symmetry

2. The number of lines of Symmetry of a regular Pentagon is  1

3. The number of lines of symmetry of an isosceles right-angled triangle is 1

4. The angle of rotation symmetry of a parallelogram is 180°

5. ______ triangle has only one line of Symmetry. Isosceles

Question 4. Which of the following figures has two lines of Symmetry and the angles or rotational symmetry is 180°
Solution:

→ Rectangle has two lines of Symmetry and angles or rotational symmetry is 180°

→ Parallelogram has no axis of Symmetry

→ It has No Angle of rotational symmetry.

→ Isosceles trapezium has 1 line of Symmetry.

→ It has No Angle of rotational symmetry

→ Square has 4 lines of symmetry

→ Angle of rotational Symmetry is +90°

Class 7 Geometry Chapter 9 Important Questions

Question 5.

1. what is symmetry?
Solution:

→Symmetry means an exact similarity in shape and size between parts of an object of a figure.

2. what is a line of symmetry?
Solution:

A figure is said to be a line of Symmetry of linear symmetry of these exists a straight line that divides into two identical halves that completely coincide with each other when folded about that line.

The straight line is called the line of symmetry of the line of reflection

3. what is rotational symmetry?
Solution:

→ In a Figure that coincides with its images when it is rotated about a point through an angle less than 360° the Figure is said to be rotational Symmetry.

The point across which the Figure rotates is called the center of rotation.

WBBSE Class 7 Maths Geometry Chapter 9 

4. what is the angle of rotational symmetry?
Solution:

For a Figure or object that has rotational symmetry the angle of turning during rotation is called the angle of rotation.

For Example: when a square is rotated by qo’ it appears the same after rotation. So the angle of rotation of the Square is 90°

Question 6. Find the angles of rotation of the following.

1. Trapezium
2. Rhombus
3. Equilateral triangle

Solution:

1. Trapezium has No out angle of rotation.
2. The rhombus has a 180° out angle of rotation.
3. An equilateral triangle has a 120° out angle of rotation

Geometry Chapter 7 Types Of Quadrilateral

Question 1. Choose the correct Answer

1. The measurement of the sum of four angles of any quadrilateral is

1. 90°
2. 180°
3. 360°
4. None of these.

∴ Option (3)360° is the correct answer

2. The each angle of a rectangle is.

1. Acute Angle
2. Right angle
3. Obtuse angle,
4. None of these

∴ Option (2) right angle is the correct answer

Read and Learn More Class 7 Maths Solutions

3. The opposite angles of the parallelogram are

1. Equal
2. Nonequal
3. Complementary
4. None of these.

∴ Option (1) equal is the correct answer

WBBSE Class 7 Maths Geometry Chapter 7

4. The angle of each square is.

1. Acute Angle,
2. Right angle,
3. Obtuse triangle
4. None of these

∴ Option (2) right angle is the correct answer.

Question 2. Write true or false

1. An isocelges trapezium is a parall dogram. → False

2. The diagonals of a rectangle bisect each other at right angles → The statement is False

3. Quadrilateral has two diagonals → The Statement is True

Question 3. Fill in the blanks:

1. The sum of the measurement of two adjacent angles of a parallelogram is 180°

2. The opposite sides of a parallelogram are Parallel to each other.

3. Quadrilateral has two diagonals

4. The length of the diagonals of an isosceles trapezium is equal.

Question 4. Each rhombus is a special type of square Explain.
Solution:

1. Every square is a rhombus (since all sides are equal and the diagonals, bisect each other at right angles
2. Not every rhombus is a square (since a rhombus does not require right angles between its sides.
3. Thus, while a square can be considered a special type of Thombus due to its right angles, a rhombus cannot be considered a type of square unless it also has right angles.

Class 7 Geometry Chapter 7 Exercise Solutions

Question 5. Write the difference between the Parallelogram and the rectangle.
Solution:

Class 7 Maths Chapter 7 Geometry PDF

Question 6. Write the difference between a rectangle and a square
Solution:

Question 7. Write the properties of the parallelogram
Solution:

Properties of parallelogram

1. Each pair of opposite sides are parallel to each other.
2. Each pair of opposite sides is equal in length
3. Each pair of opposite sides is equal in length
4. Each pair of consecutive angles sum to 180°
5. The diagonals of a parallelogram bisect each other meaning they cut each other into two equal parts.
6. The area of the parallelogram can be calculated using the formula
   1. Area = Base x Height (where Height is the perpendicular distance between the bases).
7. when transversal crosses the parallelo gram, alternate interior angles, are equal.
8. If one pair of opposite sides is both parallel and equal the quadrilateral is a parallelogram.

WBBSE Solutions for Class 7 Maths Chapter 7

Question 8. What is a convex quadrilateral, and what is a concave quadrilateral
Solution:

Convex Quadrilateral

A convex quadrilateral is a four-sided Polygon that has interior angles that measure less than 180° each The diagonals are contained entirely inside of these quadrilaterals. PQRS is a convex Quadrilateral.

Concave Quadrilateral:

If the quadrilateral has an interior angle greater than 180° It is called a concave quadrilateral.

ABCD is a quadrilateral whose interior ∠BCD >180°

Geometry Chapter 6 Parallel Lines And Transversal

Question 1. What are parallel lines?
Solution:

Parallel lines: If two straight lines on the same Plane do not intersect when produced in any direction the two straight lines are said to be parallel to one another.

In the Below Figure the straight line, AB, CD, and EF are parallel to each other i.e., AB || CD || EF

Question 2. what are vertically opposite Angles?
Solution:

Read and Learn More Class 7 Maths Solutions

Vertically Opposite Angles: If two straight lines intersect at a point, the angles formed on the opposite sides of the common point (vertex) are called vertically opposite angles. Here are two straight lines AB, CD interest at ‘O’. ∠AOC, ∠BOD are two vertically opposite angles.

Also LAOD, ∠Boc are two vertically opposite angles.

WBBSE Class 7 Maths Geometry Chapter 6

Question 3. what are corresponding angles?
Solution:

Corresponding Angles: Two angles lying on the same side of the transversal are known as corresponding angles if both lie either above are below the two given lines.

There are four pairs of corresponding angles.

(∠1, ∠5), (∠2,∠6), (∠8,∠4), and (∠7, ∠3).

Question 4. what is alternate Angles?
Solution:

Alternate Angles: The pair of interior angles on the opposite side of the transversal are called alternate angles.

There are two pairs of alternate angles (∠4,∠6), (∠3,∠5)

Class 7 Geometry Chapter 6 Exercise Solutions

Question 5. From the Figure write down the pairs of corresponding angles, alternate angles, and vertically opposite angles.

Corresponding Angles:- (∠1,∠5), (∠2, ∠6) (∠8,∠4), and (∠7, ∠3).

Alternate Angles: (∠4, ∠6) and (∠3, ∠5).

Vertically opposite Angles: (∠AGE, ∠OHF) (∠EGB, ∠CHF)

Question 6. In the adjacent Figure AB II CD Find the value of (∠BGH + ∠GHD)
Solution:

∴ The Sum of the measurement of two interior angles on the same side of the transversal is 180°

∴ ∠BGH + ∠GHD = 180°

Class 7 Maths Chapter 6 Geometry PDF

Question 7. In the adjacent Figure, ABIICD, IF ∠EGB= 40° then find the value of ∠AGH, ∠AGE, ∠BGH, ∠GHD, ∠GHC, ∠CHF, ∠DHF
Solution:

∠EGB = 40°

∠AGH = 40° Transversal the corresponding angles are equal.

∠AGE = 40° is an external angle to ∠EGB. exterior angle theorem ∠AGE = ∠EGB

∠BGH = 40° LBGH is the corresponding angle to ∠EGB.∠BGH = ∠EGB = 40°

∠GHD = 140° The corresponding angles on the same side ∠GHD+ ∠BGH = 180° ∠GHD = 180 – 40 = 140°

∠GHC = 40° LGHC corresponds to ∠AGH. ∠GHC = ∠AGH =40°

∠CHF = 140°

∠DHF = 140° ∠DHF Corresponds to ∠GHD.

∠DHF = ∠GHD = 140°

Geometry Chapter 4 Construction Of Triangles

Question 1. The length of the three sides of the triangle is given. Identify the cases where triangles can be Constructed or not Give reasons for the cases. 3.5cm, 4.5cm, 8cm

Solution:

Triangle inequality Theorem

This theorem states that the sum of the lengths Of any two sides of a triangle must be greater than the length of the third side.

Triangle having sides a, b, c

1. a+b> c
2. a+c>b
3. b+c>a

1. 3.5cm, 4.5cm, 8cm

⇒ a = 3.5cm,

b = 45cm,

C = 8cm.

b + c > a

4.5+8 >3.5

12.5>3.5

∴ with these sides of a triangle Can be constructed.

Class 7 Geometry Chapter 4 Solutions

Read and Learn More Class 7 Maths Solutions

2. 3cm, 4cm, 5cm.

Let a = 3cm, (From Triangle inequality Theorem)

a+b > c

3+4 > 5

7>5

b = 4cm,

a+c>b

3+5 > 4

8>4

c=5cm

a+c > a

4+53

9>3

∴ with the sides of a, b, c lan constructed a triangle. is possible.

3. 4cm, 5cm, 10cm

Let a = 4cm, b=5cm, c = 10cm (from Triangle inequality Theorem)

a+b > c ⇒ 4+5>10 → False

a+c > b ⇒ 4+10>5 → True

b+c > a ⇒ 5+10>4 → True

∴ with this three side, we can construct a triangle in two ways.

4. 6cm, 7cm, 8cm.

Let a = 6cm, b= 7cm, c=8cm (From Triangle inequality Theorem)

a+b > c ⇒ 6 +7 > 8 → False

a+c > b ⇒ 6 7 8 > 7 → True

b+c > a ⇒ 7+876 → True.

∴ with these three sides, we can construct a triangle in two ways.

5. 6·4cm, 5.5cm, 7cm

Let a = 6·4cm, b = 5.5cm, c = 7cm (Triangle inequality Theorety.

a+b > c ⇒ 6·4 + 5.5 > 7 → True

a+c > b ⇒ 6·4+7 > 5.5 -> True

b+c>a ⇒ 5.5 +7 > 6·4 → True

∴ with the three given sides, we can draw the triangle.

Class 7 Maths Geometry Important Questions

Question 2. Draw a triangle ABC in which AB = 4.5cm, BC= 6cm, and CA = 7.5cm. Also, measure its three angles with a protractor and write their measure.

Solution:

Given:

AB = 4.5cm

BC= 6cm

CA = 7.5m

∠ABC = 90°

∠BCA = 35°

∠САВ = 55°

1. Draw a line segment BC of length 6cm with the help of Scale and pencil
2. Take the compass with a measurement of 4.5cm, and Draw an Arc From point B.
3. Next, take measurement of 7.5cm. Draw an Arc From point ‘C’
4. Mark the Joining points of the Arc and connect the Sides of a triangle with the point.
5. Measuring the angle of a triangle with a protractor and noting down

Question 3. Construct an equilateral triangle having each side =5.5cm. Also, measure its angles.

Solution:

1. Draw a Base of the length of 5.5cm with the help of a Scale and pencil
2. Next, take the compass with a pencil take the measurement of 5.5cm and make an Arc From both sides of the line segment of the triangle Base
3. Mark the Joining of Arcs
4. Connect the lines from the Arc to both sides of the base of a triangle.
5. All the sides of a triangle have a measurement of 5.5cm
6. Measuring that all angles of a triangle are equal ie 60°
7. Construction of the equilateral triangle is completed

Class 7 Maths Chapter 4 Geometry PDF

Question 4. Draw an isosceles triangle, the base of which is 4.8cm and the sum of the base angles of which is 105°
Solution:

sum of Base Angle = \(\frac{105}{2}\) = 52.5

1. Draw a baseline of 4.8cm with the help of Scale and pencil.
2. Given that the sum of base angles is 105° divided into 2 parts each angle has 52.5°
3. Take a protractor and make the two angles of the baseline Draw a line through the angles until they intersect at a point:
4. Now the Isosceles triangle with a base length of 4.8cm and a base angle of 52.5cm is formed.

Question 5. Draw a triangle PQR in which QR = 7cm, ∠PQR = 30°, and ∠PRG=60° measure the third angle.
Solution:

1. Draw a line segment QR with a measurement of 7cm.
2. Make the 30° Angle from the side and mark a point.
3. Next, make the 60° Angle from the R side and mark a point.
4. Now extend or draw a line with the particular angles made at a point where both lines will intersect each other and Note down that point as ‘p’
5. Now take the protractor and measure the angle third angle it is 90°

Question 6. Draw a right angle triangle ABC in which AB=3cm, BC=4CM and ∠ABC = 90° Measure the length of the hypotenuse
Solution:

1. Draw a line segment of length 4C and mark it as BC, with the help of scale and pencil
2. Now make a 90° angle from point ‘B’ Draw a line Connect the angle.
3. Next cut off the line with 3cm length and mark the point as ‘A’
4. Joining the ‘Ac’ to form a right-angle triangle
5. Now measure the length of ‘Ac’ and Note down the length of the hypotenuse is 5cm

WBBSE Class 7 Geometry Answers

Question 7. Draw an Isosceles right-angled triangle PQR in which the length of hypotenuse PR is 10cm
Solution:

1. Draw the hypotenuse PR of 10cm with the help of a scale and pencil.
2. Next, make a bisector of PR by taking more than half of its length and making or drawing an arc on both sides.
3. Connect the bisector. and take the compass and adjust to the midpoint PR where the bisector intersects and with the radius make the semi-circle as shown.
4. Make a point where the Bisector and semicircle meets Note it and Join the the lines from PQ, and RQ. Isosceles right-angled triangle is formed.

Question 8. Draw a right-angled triangle ABC such that ∠ACB=90°. AB=7.5cm and ∠ABC = 30°
Solution:

Given AB = 7.5cm

∠ACB 90°, ∠ABC = 30°

Let the third angle be ‘x’

A sum of angles in a Δle = 180°

90°+30°+2° = 180°

х° = 180°-120°

x = 60°

∴ ∠BAC = 60°

1. Draw AB with 7.5 cm
2. Take the compass with some radius and draw an arc from A and Bas shown
3. From the meeting point of the arc on AB draw an area on the first area which will make 600 Angles. Same as on the other side.
4. Next, Draw the two Arcs from the intersection of two arcs on the B side. and the intersection of the Arc on AB. which makes the intersection” of the Points make 30° Angle.

5. Now take the midpoint of AB as the radius and draw a semicircle.

6. Now extend or draw the lines from A and B with the given. angle. which meet at a semicircle which makes a 90° angle

∴ The right-angled triangle is formed.

WBBSE Class 7 Geometry Answers

Question 9. Draw an isosceles triangle ABC in which AB = AC=6cm and BC=4.8cm. Draw AD⊥BC and measure the length of A.D.
Solution:

1. Draw a line segment with a length of 6cm and name it AB with the help of scale and pencil.
2. Take a compass with a measurement of 6cm and draw an Arc From point ‘A’
3. Take the measurement of 4.8cm and draw an Arc From point ‘B’ and these two Arc intersect at a point mark the point as ‘C’
4. Now Joining the other sides of the triangle to point ‘C’ the triangle ABC is formed.
5. Draw a perpendicular to BC and Name it ‘D’ Next find the length of ‘AD’ with the help of scale.
6. The length of AD is 5.5cm.

Question 10. Draw an isosceles triangle ABC in which the length of base BC is 4.8cm and the length of perpendicular AD.
Solution:

1. Draw a baseline of length BC = 4.8cm with the help of Scale and pencil.
2. Take the with any radius and draw an Arc from point B and point as shown.
3. Next, take the compass and put the compass at the intersection of the baseline Arc which makes the angle of 60°. Do it on Both sides of the Intersection.
4. Next, extend the lines through the Intersection of the two arcs. The extended lines form a triangle at point ‘A’
5. Draw a perpendicular to BC and Name it ‘AD’

Arithmetic Chapter 4 Approximation Of Values

Question 1. Determine the approximate value of 5378 up to tens, hundreds, and thousands of places.

Solution:

5378

5-Thousand

3-Hundred

7-Tens

8-units

The number at the tens place is 7 and on its immediate right side is 8 which is between 5 to 9.

So up to tens place the approximate value is (537+1)ten

= 5380

The digit on the hundreds place is 3 and on its immediate right side is 7 So the approximate value upto hundreds place is 5300

The digit on the thousands place is 5 and on its. right side we have 3, so the approximate value. up to a thousand places is 6000

5378 ≈ 5380 (upto tens place).

5378 ≈ 5400 (upto Hundreds place)

5378 ≈ 5000 (upto Thousands place).

Read and Learn More Class 7 Maths Solutions

Class 7 Maths Arithmetic Chapter 4 Solutions

Question 2. Find the approximate value of 6.748564 up to whole number and 1, 2, 3, 4, and 5 decimal places

Solution:

6.748564 ≈ The number is up to 6th place is 4

6.748564 16.748571 [5th place after the decimal is 6 Hence 1 is added to 5th decimal place value 6, 6+1=7]

6.748564 ≈ 6.7486 [ 4th place after decimal is 6 Hence 1 is added to 3rd place value 5, 5+1=6

6.748564 ≈ 6.749[3rd place after decimal is 5 Hence 1 is added to 2nd place value 8, 8+1=9]

6.748564 ≈ 6.75 [2nd place after decimal is 4 Hence 1 is added to 1 decimal place value 44+1=5]

6.748564 ≈ 6.8

6.748564 ≈ 6.74856

≈ 6.7486

≈ 6.749

≈ 6.75

≈ 6.8

≈ 7

Question 3. Find the approximate value of \(5 \frac{7}{37}\) upto 2,3,4 and 5 decimal place
Solution:

⇒ \(5 \frac{7}{37} \Rightarrow \frac{192}{37}\)

⇒ \(5 \frac{7}{37}\) = 5.18 [TWO decimal place]

⇒ \(5 \frac{7}{37}\)= 5.189 [3 decimal place]

⇒ \(5 \frac{7}{37}\) = 5.1891 [4 decimal place]

⇒ \(5 \frac{7}{37}\) = 5.18918 [5 decimal place]

Class 7 Arithmetic Chapter 4 Questions

Question 4. Divide ₹37 among 5 boys and 3 girls equally. Find how much each would get. (approximated upto 2 places of decimal) Also, find the total money received by 5 boys and 3 girls and how much this total amount is more or less than ₹37

Solution:

The total number of boys and girls is (5+3) or 8

₹37 is divided among 8$ boys and girls

Each gets = ₹\(\frac{37}{8}\)

= 4.625 paise

The total money received by 5 boys is

= (4.625×5) paise

= 23.125 paise

The total money received by 3 girls is

= (4.625×3) Paise

= 13.875 Paise

Total money received by 5 boys and 3 girls is (23.125+13-87)

=₹37

This amount is equal to ₹37

WBBSE Class 7 Maths Solutions

Question 5. Simplify the following up to 3 decimal places. 21-3574 + 5.72 + 3.602

Solution:

21.3574+ 5.727272… +3.602602.

⇒ 30.687202.

Rounded the decimal upto

3 digits i.e. 30.687

⇒ \(\begin{array}{r}
21.3574 \\
+5.7272 \\
+3.602602 \\
\hline 30.687201 \\
\hline
\end{array}\)

Question 6. Find the difference between 47.286 and 28.6 upto 2 places of decimal

Solution:

Given:

First number = 47.286

Second number = 28.6

The difference = (First number) – (second number)

= 47.286 28.6

= 18.686

Rounded to two decimals places the difference is 18.69

Class 7 Arithmetic Textbook Solutions

Question 7. If 1 inch = 2.54 cm then find the value of 1cm into an inch upto 3 decimal places.

Solution:

Given:

1 inch = 2.54cm.

So to find how many inches are in 1 centimeter

we’ll divide by 2:54

⇒ \(\frac{1}{2.54} \approx 0.3937 .\)

The Rounded to three decimals places, 1 centimeter is approximately equal to 0.394 inches.

Question 8. Write the approximate value of the following numbers upto lacs thousands and hundreds of places.

Solution:

Question 9. Find the values of the following correct to 3 places of decimals.

1. \(7 \frac{2}{7}\)
2. \(3 \frac{8}{45}\)
3. 8.0645

Solution:

1. \(7 \frac{2}{7}\)

⇒ \(\frac{51}{7}\)

⇒ 7.285714….

Rounded to three decimals places it’s approximately 7.286

2. \(3 \frac{8}{45}\)

⇒ \(3 \frac{8}{45}\)

⇒ \(\frac{143}{45}\)

= 3.17778 ≈ 3.178

3. 8.0645

Rounded to three decimal places It’s approximately 8.064

Class 7 Maths Arithmetic Problems

Question 10. Simplify and Find the approximate value upto 1 decimal place.

⇒ \(7 \frac{2}{3} \times \frac{4}{5} \div \frac{3}{4} \text { of } \frac{2}{3}\)

Solution:

⇒ \(7 \frac{2}{3} \times \frac{4}{5} \div \frac{3}{4} \text { of } \frac{2}{3}\)

⇒ \(7 \frac{2}{3} \times \frac{4}{5} \div \frac{3}{4} \times \frac{2}{3}\)

⇒ \(\frac{23}{3} \times \frac{4}{5} \div \frac{3}{4} \times \frac{2}{3}\)

⇒ \(\frac{92}{15} \div \frac{6}{4}\)

⇒ \(\frac{\frac{92}{15}}{\frac{6}{4}}\)

⇒ \(\frac{92}{15} \times \frac{4}{6}=\frac{368}{90}=4.0\)

⇒ \(7 \frac{2}{3} \times \frac{4}{5} \div \frac{3}{4} \text { of } \frac{2}{3} \text { is } 4.0\)

Class 7 Maths Solutions For Arithmetic Chapter 5 Square Root Of Fractions

Question 1. Choose the correct answers.

The least positive integer which will multiply \(\frac{144}{605}\) to make it perfect square is

1. 3
2. 5
3. 7
4. 11

⇒ \(\frac{144}{605}=\frac{2 \times 2 \times 6 \times 6}{5 \times 11 \times 11}\)

⇒ \(\frac{2^2 \times 6^2}{11^2 \times 5}\)

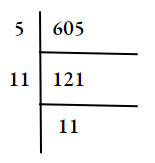
So \(\frac{144}{605}\) is to be divided by the least positive integer

5 so as to make it a perfect square fraction.

So the correct answer is (2) 5

Class 7 Arithmetic Chapter 5 Exercise Solutions 

Question 2. Write true or False

1.5128 is a perfect decimal Square → False

2. The value of \(\sqrt{0.0256}+\sqrt{2.56}+\sqrt{0.000256}\) is 1.776.

⇒ \(\sqrt{0.0256}+\sqrt{2.56}+\sqrt{0.000256}\)

⇒ 0.16 + 1·6+0-016

⇒ 1.776 → True

3. The square root of \(3 \frac{109}{225} \text { is } 1 \frac{13}{15}\)

⇒ \(3 \frac{109}{225}\)

⇒ \(\frac{784}{225}\)

⇒ \(\sqrt{\frac{784}{225}}\)

⇒ \(\frac{28}{15}\)

⇒ \(1 \frac{13}{15}\) → True

Question 3. Fill In the blanks:

1. If \(\sqrt{\frac{x}{225}}=\sqrt{\frac{9}{25}}\) then the value of x is 81

⇒ \(\sqrt{\frac{x}{225}}=\sqrt{\frac{9}{25}}\)

⇒ \(\frac{\sqrt{x}}{\sqrt{225}}=\frac{\sqrt{9}}{\sqrt{25}}\)

⇒ \(\frac{\sqrt{x}}{15}=\frac{3}{5}\)

⇒ \(5 \sqrt{x}=3 \times 15\)

⇒ \(\sqrt{x}=\frac{45}{5}\)

⇒ \(\sqrt{x}=9\)

squaring on Both sides.

⇒ \((\sqrt{x})^2=(9)^2\)

x =81

2. If \(\sqrt{1024}\) = 32 then the value of \(\sqrt{10.24}+\sqrt{0.1024}+\sqrt{0.001024}\) is 3.552

⇒ \(\sqrt{10.24}+\sqrt{0.1024}+\sqrt{0.001024}\)

Given \(\sqrt{1024}=32\)

⇒ \(10.24=10.24 \times 1=(32 \times 0.32)=\left(\frac{32}{10}\right)^2\)

⇒\(\sqrt{10.24}=\sqrt{\left(\frac{32}{10}\right)^2}=\frac{32}{10}=3.2\)

⇒ \(0.1024=0.1024 \times 1=\left(\frac{32}{100}\right)^2=\left(\frac{32}{10^2}\right)^2\)

⇒ \(\sqrt{0.1024}=\sqrt{\left(\frac{32}{100}\right)^2}=\frac{32}{100}=0.32\)

⇒ \(0.001024=0.001024 \times 1=\left(\frac{32}{1000}\right)^2=\left(\frac{32}{10^3}\right)^2\)

⇒\(\sqrt{0.001024}=\sqrt{\left(\frac{32}{1000}\right)^2}=\frac{32}{1000}=0.032\)

⇒\(\sqrt{10.24}+\sqrt{0.1024}+\sqrt{0.001024}\)

⇒ 3.2 + 0.32 + 0.032

⇒ 3.552

Class 7 Arithmetic Chapter 5 Important Questions

Question 4. Find the value of \(\sqrt{\sqrt{\frac{1 \cdot 44}{0.25}}+\sqrt{\frac{0.64}{0.25}}}\)

Solution.

Given

⇒ \(\sqrt{\sqrt{\frac{1 \cdot 44}{0.25}}+\sqrt{\frac{0.64}{0.25}}}\)

⇒ \(\sqrt{\frac{\sqrt{1.44}}{\sqrt{0.25}}+\frac{\sqrt{0.64}}{\sqrt{0.25}}}\)

⇒ \(\sqrt{\frac{1.2}{0.5}+\frac{0.8}{0.5}}\)

⇒ \(\sqrt{2 \cdot 4+1 \cdot 6}\)

⇒ \(\sqrt{4}\)

= 2

⇒ \(\sqrt{\sqrt{\frac{1 \cdot 44}{0.25}}+\sqrt{\frac{0.64}{0.25}}}\) = 2

Question 5. Find the length of each side of a square whose area is equal to the sum of the two squares having the lengths of each side 1.2m and 0.5m respectively

Solution:

Given:

Length of First Square side = 1.2m

Length of second square side = 0.5m

The area of the First square

Area 1 = (1.2m)² = 1044 m²

The area of the second square

Arear = (0.5m)² = 0.25 m²

Total Area = Area 1 + Area2 = 1.44m² +0.25 m² = 1.69m²

Side length = \(\sqrt{\text { Total Area }}\)

⇒ \(\sqrt{1.69 \mathrm{~m}^2}\)

= 1.3m

∴ The length of each side of the new square is 1.3 meters.

Class 7 Maths Arithmetic Chapter 5 Notes

Question 6. If product of two positive number is \(\frac{12}{25}\) and their quotient is \(1 \frac{26}{49}\) then find the numbers.

Solution:

Let the two positive numbers be ‘x’ and ‘y’.

According to Question xxy = \(\frac{12}{25}\) and \(\frac{x}{y}\) = \(1 \frac{26}{49}\)

⇒ \(x \times y \times \frac{x}{y}=\frac{12}{25} \times \frac{75}{49}\)

⇒ \(x^2=\frac{900}{1225}\)

⇒ \(x=\sqrt{\frac{900}{1225}}\)

⇒ \(x=\frac{30}{35}=\frac{6}{7}\)

⇒ \(x=\frac{6}{7}\)

⇒ xxy = \(\frac{12}{25}\)

⇒ \(\frac{6}{7} x y=\frac{12}{25}\)

⇒ \(y=\frac{12}{25} \times \frac{7}{6}\)

⇒ \(y=\frac{14}{25}\)

The two numbers are $ and \(\frac{6}{7}\) and \(\frac{14}{25}\)

Question 7. Find the approximate value of the following Upto 3 decimal places:-

1. \(\sqrt{3}\)
2. \(\sqrt{5}\)
3. \(\sqrt{18}\)

1. \(\sqrt{3}\)

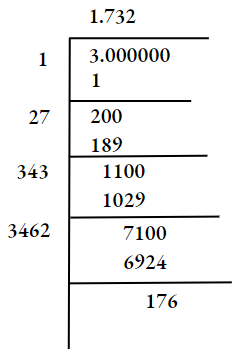
∴ \(\sqrt{3} \simeq 1.732\)

2. \(\sqrt{5}\)

∴ \(\sqrt{5}=2.236\)

3. \(\sqrt{18}\)

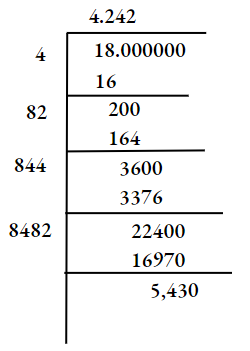
∴ \(\sqrt{18}=4.242\)

Class 7 Maths Chapter 5 Arithmetic PDF

Question 8. Find the square root of the following.

Solution:

1. \(4 \frac{220}{729}\)

⇒ \(\frac{3136}{729}\)

⇒ \(\sqrt{\frac{3136}{729}}\)

⇒ \(\frac{56}{27}\)

= 2.0740

∴ \(\sqrt{4 \frac{220}{729}}=\frac{56}{27}\)

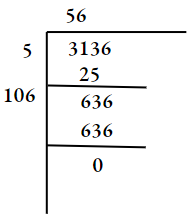
2. 206.094736

⇒ \(\sqrt{206.094736}\) = 14.357

3. 10732.96

⇒ \(\sqrt{10732.96}\) = 103.6

4. \(3 \frac{1321}{2025}\)

⇒ \(\frac{7396}{2025}\)

⇒ \(\sqrt{\frac{7396}{2025}}\)

⇒ \(\frac{86}{45}\)

⇒ \(1 \frac{41}{45}\)

∴ \(\sqrt{3 \frac{1321}{2025}}=1 \frac{41}{45}\)

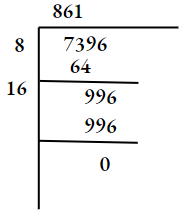
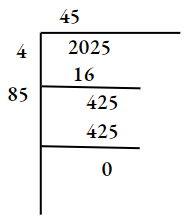
Question 9. What is the least number that must be subtracted From 0.001528?

Solution:

⇒ \(0.001528 \approx \sqrt{\frac{1528}{1000000}} \approx \frac{\sqrt{1528}}{1000} \approx \frac{39.08}{1000} \approx 0.03908\)

⇒ \((0.039)^2=0.039^2=0.001521\)

⇒ \((0.040)^2=0.040^2=0.001600\)\

The closest perfect square less than 0.001528 is 0.001521

Now subtract this value from 0·001528:

0.001528 – 0.001521 = 0·000007.

∴ The least number that must be subtracted from 0.001528 to make it a perfect Square number is 0.000007.

Class 7 Maths Chapter 5 Arithmetic PDF

Question 10. Find the value of \(\sqrt{1-(0.05)^2}\) upto 3 decimal places.

Solution:

⇒ \(\sqrt{1-(0.05)^2}\)

⇒ \(\sqrt{1-0.0025}\)

⇒ \(\sqrt{0.9975}\)

= 0·998749

Rounded upto 3 decimals = 0.998

Question 11. By which Fraction should \(\frac{35}{91}\) be multiplied so that the square root of the product is 3?

Solution:

Let the Fraction be \(\frac{a}{b}\)

⇒ \(\sqrt{\left(\frac{35}{91} \times \frac{a}{b}\right)}=3\)

⇒ \(\frac{35}{91} \times \frac{a}{b}=3^2\)

⇒ \(\frac{35}{91} \times \frac{a}{b}=9\)

⇒ \(\frac{35}{91}=\frac{5 \times 7}{7 \times 13}=\frac{5}{13}\)

Substitute \(\frac{5}{13} \text { for } \frac{35}{91}\)

⇒ \(\frac{a}{b}=9 \times \frac{13}{5}=\frac{117}{5}\)

⇒ \(\frac{35}{91} \times \frac{117}{5}=\frac{35 \times 117}{91 \times 5}=\frac{5 \times 7 \times 117}{7 \times 13 \times 5}=\frac{117}{13}=9\)

⇒ \(\sqrt{9}=3\)

Hence the Fraction \(\frac{117}{5}\) is correct.

Thus the Fraction by which \(\frac{35}{91}\) should be multiplied so that the square root of the product is 3 is

⇒ \(\frac{117}{5} \Rightarrow 23 \frac{2}{5}\)

Geometry Chapter 1 Revision Of Old Lesson

Question 1. Choose the correct answer

1. The acute angle is

1. 30°
2. 90°
3. 105°
4. 270°

The acute Angle lies between 0° to 90°

∴ The option (1) 30° is the correct answer

Class 7 Maths Geometry Chapter 1 Solutions

2. The surface of the pyramid is.

1. Rectangle
2. Square
3. Triangle
4. None of these

∴ The option (3) triangle is the correct answer.

Read and Learn More Class 7 Maths Solutions

3. The number of vertices of a cube is

1. 4
2. 6
3. 8
4. 12

∴ The option (3) 8 is the correct answer

Question 2. write true or false

1. Only one curved line can be drawn through two points. → False

2. Two straight lines can be drawn through two Fixed points → False

3. 120° is an obtuse angle → True

Class 7 Geometry Chapter 1 Questions

Question 3. Fill in the blanks

1. The greatest chord of a circle is known as the Diameter
2. 180° is called a straight angle
3. Many straight lines can be drawn through one fixed point.

Question 4. write the definition with a Figure of the Following

1. Adjacent angle

Adjacent angles: are two angles that share a common side and a common vertex, and do not overlap.

In the given diagram ∠ABD and ∠CBD are adjacent angles.

They share the common arm or common side BD and a common vertex B.

2. Vertically opposite angle

vertically opposite angles are angles that are opposite one another at a specific vertex and are created by two straight intersecting lines.

vertically opposite angles are equal to each other.

WBBSE Class 7 Maths Geometry Solutions

3. Reflex Angle:

A reflex Angle is an angle that is more than 180° and less than 360°

4. Straight Angle

A straight angle measures 180° and looks like a straight line

Mathematically

It is an angle whose arms lie in opposite directions from the vertex and they join together to form 180°.

5. Obtuse Angle

An angle that is larger than go but smaller than 180° is called an obtuse angle.

Question 5. Draw a line segment of length 10cm with a scale and divide it into four equal parts. Measure
Solution:

Line segment AB = 10cm

It is divided into ‘4’ equal parts.

Each part is divided into 2.5CM

AC = 2.5cm,

CD = 2.5 cm,

DE = 2.5 CM,

EB = 2.5 cm

∴ AB = AC+ CD +DE+EB

= 2·5+2·5+2·5+2·5

AB = 10cm

∴ The parts are equal AC = CD= DE = EB.

Class 7 Geometry Textbook Solutions 

Question 6. Draw an angle of 120° with the help of a protractor and divide it into four equal parts with the help of a compass.
Solution:

∠BOA = 120°

∠OAE = 30°

∠AOD = 60°

∠AOC = 90°

Question 7. Draw a triangle ABC and bisect each of the three angles and find if the angle bisectors are concurrent.
Solution:

Question 8. Draw a triangle ABC and bisect the sides BC, AC, and AB perpendicularly. If the three perpendicular bisectors are concurrent then name it’ Now with. center o and radius equal to the line segment AO draw a circle.
Solution:

Class 7 Maths Geometry Problems

Question 9. Draw a triangle PQR and from the three vertices P, Q, and R of the triangle, perpendicular PA, BQ, and RC are drawn on the sides QR, RP, and PQ respectively If the line segment PA, QB, and RC are concurrent.
Solution:

Question 10. A line segment AB of length 6cm is drawn. A point p is taken on the line segment AB. With the help of a scale and pencil compass draw a perpendicular PQ on AB at p.
Solution:

1. Draw a line segment AB of length 6cm
2. Draw a point ‘P’ on a line segment
3. Draw a perpendicular on ‘AB’.

Geometry Chapter 2 Drawing Angles With Compass

Question 1. Draw the following angles using a scale, pencil 1350, and compass.

1. 1.5°
2. \(22 \frac{1}{2}^{\circ}\)
3. 30°
4. 45°
5. 60°
6. \(7 \frac{1}{2}^{\circ}\)
7. 75°
8. 90°
9. 105°
10. 120°
11. 135°
12. 150°

Solution:

∠AOB = \(7 \frac{1}{2}^{\circ}\)

∠AOC = 15°

Read and Learn More Class 7 Maths Solutions

∠AOD = \(22 \frac{1}{2}^{\circ}\)

∠AOE = 30°

∠AOF = 45°

∠AOG = 60°

∠AOH = 75°

∠LAOI = 90°

∠AOJ = 105°

∠AOK = 120°

∠AOL = 135°

∠AOM = 150°

Class 7 Geometry Chapter 2 Questions

Question 2. Draw an angle ABC where ∠ABC = 45° Then CB is produced to any point D. Measure the LABD using a protractor. Bisects the ∠ABC and LABD wring compass and measures the angle between the bisectors of ∠ABC and ∠ABD.

Solution:

∠ABC= 45°

∠ABD = 15°

Angle between the bisectors of ∠ABC and ∠ABD = \(37\frac{1}{2}\)

WBBSE Class 7 Maths Geometry Solutions

Question 3. Draw an angle ∠PQR without a protractor, where ∠PQR = 120° Then divide ∠PQR into four equal parts.

Solution:

∠PQA = 30°

∠PQB = 60°

∠PQC = 90°

∠PQR = 120°