WBBSE Class 10 Maths Geometry Chapter 2 Theorems Related To Tangent Of A Circle Multiple Choice Questions

WBBSE Class 10 Maths Geometry Chapter 2 Theorems Related To Tangent Of A Circle Multiple Choice Questions

Example 1. A tangent drawn to a circle with centre O from an external point A touches the circle at the point B. If OB = 5 cm, AO = 13 cm, then the length of AB is

1. 12 cm
2. 13 cm
3. 6.5 cm
4. 6 cm

Solution:

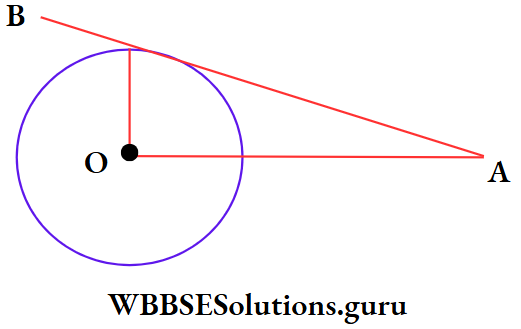
⇒ OB is radius and AB is a tangent of a circle with centre O.

∴ OB ⊥ AB

⇒ On right angled triangle AOB, ∠AOB = 90°

∴ OB² + AB² = OA²

Read And Learn Also WBBSE Class 10 Maths Multiple Choice Questions

⇒ AB = \(\sqrt{\mathrm{OA}^2-\mathrm{OB}^2}\)

= \(\sqrt{13^2-5^2} \mathrm{~cm}\)

= √144 cm = 12 cm

∴ The correct answer is 1. 12 cm’

Example 2. Two circles touch each other externally at the point C. A direct common tangent AB touch the two circles at the points A and B. Value of ∠ACB is

1. 60°
2. 45°
3. 30°
4. 90°

Solution: Tangent drawn at the point C intersects AB at the point M.

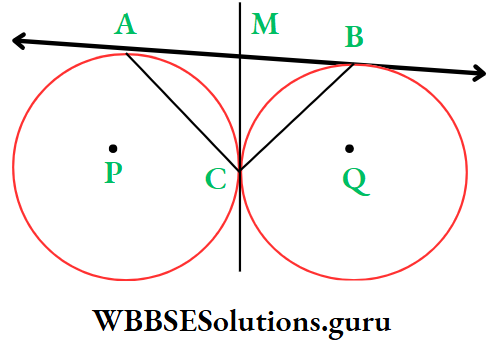
⇒ MA and MC are two tangent from the point M to a circle with P.

∴ MA = MC

⇒ Similarly, MB = MC

⇒ In ΔAMC, MA = MC

∴ ∠MCA = ∠MAC

⇒ In ΔBMC, MB = MC

⇒ ∠MCB – ∠MBC

∴ ∠MCA + ∠MCB = ∠MAC + ∠MBC

⇒ i.e. ∠ACB = ∠BAC + ∠ABC

⇒ In ΔABC, ∠ACB + ∠BAC + ∠ABC = 180°

⇒ ∠ACB + ∠ACB = 180°

⇒ 2 ∠ACB = 180°

⇒ ∠ACB = 90°

∴ The correct answer is 4. 90°

Class 10 Maths Geometry Chapter 2 MCQs 

Example 3. The length of radius of a circle with centre O is 5 cm. P is a point at the distance of 13 cm from the point O. The length of two tangents are PO and PR from the point P. The area of quadrilateral PQRS is

1. 60 sq cm
2. 30 sq cm
3. 120 sq cm
4. 150 sq cm

Solution: PQ is a tangent and OQ is the radius of the circle with centre O,

∴ OQ ⊥ PQ

∴ ∠OQP = 90°

⇒ Similarly, ∠ORP 90°

⇒ OQ = OR = 5 cm and OP = 13 cm

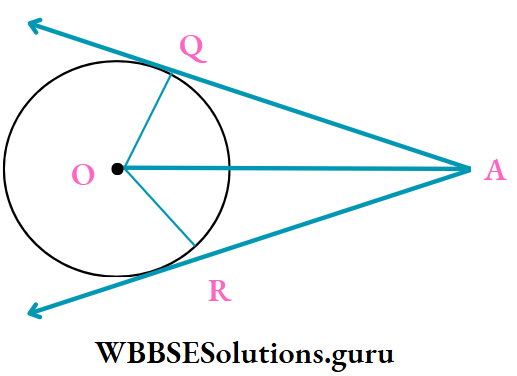
⇒ In right-angled ΔPOQ, OQ² + PQ² = OP²

⇒ PQ² = OP² – OQ²

⇒ PQ = \(\sqrt{O P^2-O Q^2}\)

= \(\sqrt{13^2-5^2} \mathrm{~cm}\)

= √144 cm = 12 cm

⇒ PQ and PR are tangents of a circle with centre O,

∴ PR = PQ = 12 cm

⇒ Area of ΔPOQ = \(\frac{1}{2}\) x PQ x OQ

= \(\left(\frac{1}{2} \times 12 \times 5\right)\) sq. cm = 30 sq. cm

⇒ Similarly, ΔPOR = 30 sq. cm

∴ Area of quadrilateral PQOR = ΔPOQ + ΔPOR = (30 + 30) sq. cm = 60 sq. cm

∴ The correct answer is 1. 60 sq cm

Class 10 Geometry Chapter 2 Mcqs With Answers

Example 4. The lengths of radii of two circles are 5 cm and 3 cm. The two circles touch each other externally. The distance between two centres of two circles is

1. 2 cm
2. 2.5 cm
3. 15 cm
4. None of these

Solution: Two circles with centre A and B touch externally each other at point P.

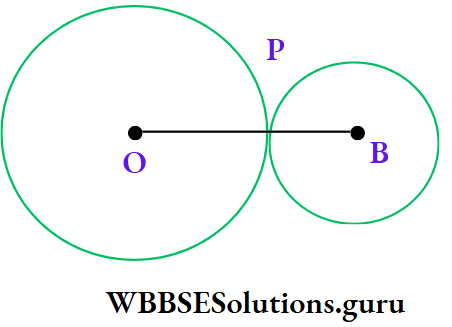
⇒ AP = 5 cm, BP = 3 cm

⇒ AP and BP lies on the same straight line

∴ AB = AP + BP = (5 + 3) cm = 8 cm.

∴ The correct answer is 4. None of these

Wbbse Class 10 Maths Geometry Notes

Example 5. The lengths of radii of two circles are 3.5 cm and 2 cm. The two circles touch each other internally. The distance between the centres of two circles is

1. 5.5 cm
2. 1 cm
3. 15 cm
4. None of these

Solution: Two circles with centres A and B touch internally each other at point C.

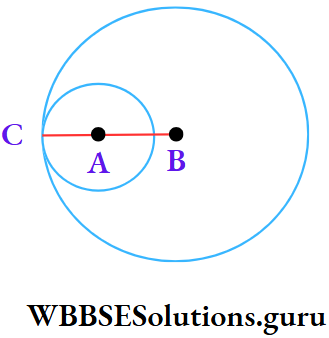
⇒ Let BC = 3.5 cm, AC = 2 cm

∴ BC and AC lies on the same straight line

⇒ AB = BC – AC = (3.5 – 2) cm = 1.5 cm

∴ The correct answer is 3. 1.5 cm