WBBSE Class 10 Maths Trigonometry Chapter 1 Concept Of Measurement Of Angle Multiple Choice Questions

WBBSE Class 10 Maths Trigonometry Chapter 1 Concept Of Measurement Of Angle Multiple Choice Questions

Example 1. The end point of the minute hand of a clock rotates in 1 hour

1. \(\frac{\pi^c}{4}\)
2. \(\frac{\pi^c}{2}\)
3. π^c
4. 2π^c

Solution: The end point of the minute hand of a clock rotates in 1 hour is 360°

Read And Learn Also WBBSE Class 10 Maths Multiple Choice Questions

180° = π^c

\(360^{\circ}=\frac{360}{180} \pi^c=2 \pi^c\)

∴ The correct answer is 4.

Example 2. \(\frac{\pi}{6}\) radian equal to

1. 60°
2. 45°
3. 90°
4. 30°

Solution: \(\frac{\pi}{6}\) radian = \(\frac{180^{\circ}}{6}\) = 30°

∴ The correct answer is 30°

Class 10 Maths Trigonometry Chapter 1 MCQs

Example 3. The circular value of each internal angle of a regular hexagon is

1. \(\frac{\pi}{3}\)
2. \(\frac{2\pi}{3}\)
3. \(\frac{\pi}{6}\)
4. \(\frac{\pi}{4}\)

Solution: The value of each internal angle of a regular hexagon is

⇒ \(\frac{2 \times 6-4}{6} \times 90^{\circ}=120^{\circ}\)

⇒ \( 180^{\circ}=\pi^c\)

⇒ \(120^{\circ}=\frac{120}{180} \pi^c=\frac{2 \pi^c}{3}\)

∴ The circular value of each angle is \(\frac{2 \pi^c}{3}\)

∴ The correct answer is 2. \(\frac{2\pi}{3}\)

Example 4. The measurement of θ in the relation to S = rθ is determined by

1. Sexagesimal system
2. Circular system
3. Those two methods
4. None of these

Solution: The correct answer is 2. Circular system

Trigonometric Ratios Mcqs Class 10

Example 5. In cyclic quadrilateral ABCD, if ∠A = 120°, then the circular value of ∠C is

1. \(\frac{\pi}{3}\)
2. \(\frac{\pi}{6}\)
3. \(\frac{\pi}{2}\)
4. \(\frac{2\pi}{3}\)

Solution: In cyclic quadrilateral ABCD, [The opposite angles of a cyclic quadrilateral are supplementary]

∠A + ∠C = 180°

120° + ∠C = 180°

⇒ ∠C = 60°

180° = π^c

∴ 60°= \(\frac{60}{180} \pi^c=\frac{\pi^c}{3}\)

∴ The correct answer is 1. \(\frac{\pi}{3}\)

 

WBBSE Notes For Class 10 Geography And Environment	WBBSE Notes For Class 10 History And Environment
WBBSE Solutions For Class 10 Life Science	WBBSE Class 10 Life Science Multiple Choice Questions
WBBSE Solutions for Class 10 Maths	WBBSE Class 10 Maths Multiple Choice Questions
WBBSE Notes For Class 10 Physical Science And Environment

 

Class 10 Trigonometry Chapter 1 Mcqs With Answers

Example 6. In ΔABC, point of intersection of ∠B and ∠C is O; if ∠BAC = 40°, then the circular value of ∠BOC is

1. \(\frac{5 \pi}{18}\)
2. \(\frac{4 \pi}{12}\)
3. \(\frac{11 \pi}{18}\)
4. \(\frac{2 \pi}{5}\)

Solution:

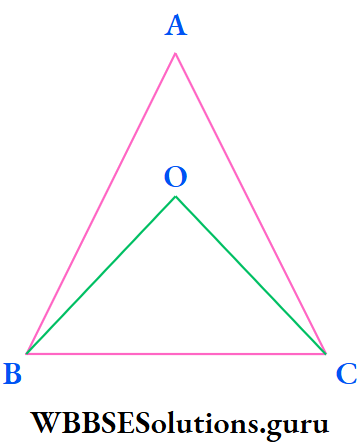
∠BOC = 90° + \(\frac{1}{2}\) ∠BAC

= 90° + \(\frac{1}{2}\) x 40° = 110°

180° = π^c

⇒ 110° = \(\frac{110}{180} \pi^c=\frac{11 \pi^c}{18}\)

∴ The correct answer is 3. \(\frac{11 \pi}{18}\)

Example 7. If ∠A + ∠B = \(\frac{5 \pi}{12}\) and ∠A – ∠B = 15° then the sexagesimal value of ∠B is

1. 45°
2. 60°
3. 75°
4. 30°

Solution:

⇒ ∠B = 30°

∴ The correct answer is 4. 30°

Trigonometric Identities Mcqs Class 10

Example 8. If O is the circumcentre of the ΔABC and ∠BOC = 120° then the circular value of ∠BAC is

1. \(\frac{\pi}{3}\)
2. \(\frac{\pi}{6}\)
3. \(\frac{2\pi}{3}\)
4. None of these

Solution:

 

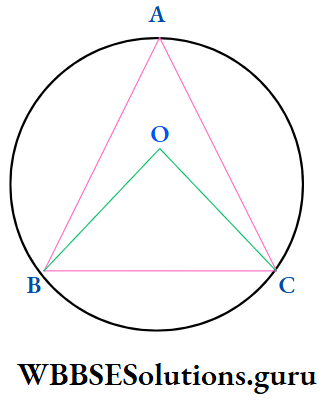
∠BOC = 2 ∠BAC

⇒ ∠BAC = \(\frac{1}{2}\) ∠BOC = \(\frac{1}{2}\) x 120° = 60°

180 = π^c

60° = \(\frac{60}{180} \pi^c=\frac{\pi^c}{3}\)

∴ The correct answer is 1. \(\frac{\pi}{3}\)