WBBSE Class 7 Maths Solutions For Algebra Chapter 2 Addition and Subtraction

Algebra Chapter 2 Exercise

Question 1. Choose the correct answers:

1. The value of (-6) x (-12) -(-4) x (+3) is

1. 60
2. -84
3. 84
4. -60

Solution:

⇒ (-6) x (-12)  – (-4) x (+3)

⇒+72 +12

⇒ +84

∴ The value of (-6) x (-12) – (-4) x (+3) is 84

Option (3) → 84 is the correct Answer

Read and Learn More Class 7 Maths Solutions

2. If x = -2, y = 3 and z = -5 then the value of (x-y+z) is

1. 0
2. -4
3. -10
4. -4

Solution:

Given that

x = -2,

y = 3

z = -5

(x-y+z)=?

∴ (x-y+z) = {(-2) – (3) + (-5)}

Here Substituted the values of x,y,z

= {(-2-3-5)}

∴ (x-y+z) = -10

Option (3)=-10 is correct.

Class 7 Algebra Problems With Solutions 

3. The value of 4(3+1)÷(-4) of (2) is

1. 2
2. -2
3. 8
4. -8

Solution:

⇒ 4(3+1) ÷ (-4) Of (-2)

⇒  4(3+1) ÷ (-4)

⇒ 4(4) ÷ (-4)

⇒ 16÷(-4)

⇒ -4

∴ -4 of (-2)

Question 2. Write true or false:

1. a ÷ (b + c) = \(\frac{a}{b} + {a}{c}\)
2. If a and b are two different integers then a + b = b + a but a-b ≠ b-a
3. For any three integers, the law of association of integers is not valid in the case of subtraction.

Solution:

1. False
2. a+b = b+a but a-b ≠ b-a; True
3. True

Question 3. Fill in the blanks

1. (-15) ÷ (-5) ÷ (-3)=
2. (-1) x (-2) x (-3) × ____ = (-5) × (-6)
3. (-20) ÷ (-4) of 5 x 2 = _____

Solution:

1. (-15)÷(+5)=(-3)

⇒ \(\frac{-15}{-5}{\frac{-3}{-1}}\)

⇒ \(\frac{-15}{-5} \times \frac{1}{-3}\)

⇒ -1

∴ (-15) ± (-5) ÷ (-3) = -1

2. (-1) x (-2 )x (-3) × _____ = (-5) x (-6)

(-1) x (-2)× (-3) × x = (-5)× (-6)

Let the number be x

⇒ 2 × (-3) x x = 30.

⇒ -3x = \(\frac{30}{2}\)

x = \(\frac{15}{-3}\)

∴ x = -5

∴ (-1) × (-2) x (-3) × (-5) = (-5) x (-6)

3. (-20) ÷ (-4) of (5 x 2 )= _____

⇒ (-20) ÷ (-4) of (5×2)

⇒ (-20) ÷ (-20) x (2)

⇒ (+1) x (2)

⇒ 2

∴ (-20) ÷ (-4) of (5 x 2) = 2

Class 7 Maths Algebra Solutions WBBSE

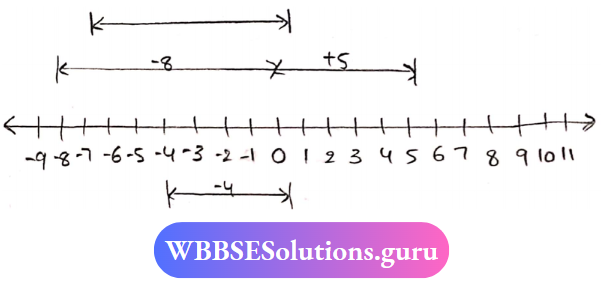
Question 4. Find the Sum with the help of a number line.

1. (-8)+(+5)+(-4)
2. (-7)+(-3)+(+10).

Solution:

1. (-8)+(+5) + (-4)

⇒ -8 + 5 -4

⇒ -12 + 5

⇒ -7

2. (-7) + (-3) + (+10)

⇒ (-7-3+10)

⇒ -10 + 10

⇒ 0

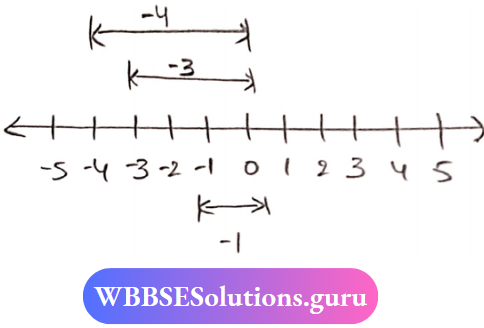
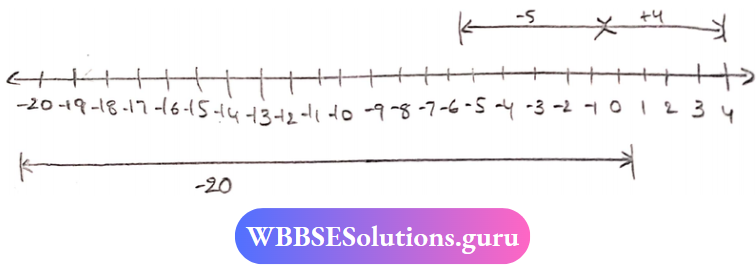
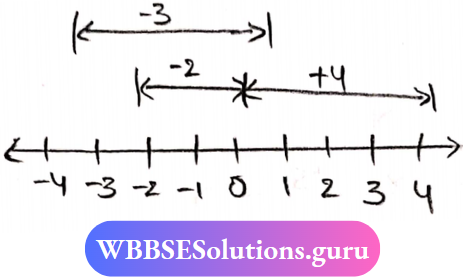
Question 5. Find the values of the following on the number line:

1. (-4)-(-3)
2. (-5)x(+4)
3. (-3)+{(+4)+(-2)}
4. (-8)÷(+2)

Solution:

1. (-4) – (-3)

⇒ -4 + 3

⇒ -1

2. (-5) x (+4)

⇒ -20

3. (-3)+{(+4)+(-2)}

⇒ (-3) + {4-2}

⇒ -3 +2

⇒ -1

4. (-8) ÷ (+2)

⇒ -4

WBBSE Class 7 Maths Chapter 2 Answers

Question 6. Verify if the distributive law of multiplication holds for integers:

1. (-5) x {(-2)+(-4)}
2. (+8) ÷ {(+4)+(-2)}

Solution:

(-5) x {(-2)+(-4)}

⇒ (-5) x {-6}

⇒ +30

Or,

(-5) x (-2) + (-5) x (-4)

⇒ (-10) + (-20)

⇒ +30

∴ (-5) × {(-2) + (-4)}

= (-5) X (2) + (-5) x (-4)

∴ The distributive face of multiplication is verified

Question 7. The temperature of Kashmir is 24°C If the temperature reduces uniformly every hour and reaches to -4°C after 7 hours. Find the rate of reduction of temperature. per hour.
Solution:

Given Data,

The temperature of Kashmir is (T_i) = 24°C

Final Temperature after 7hrs (T_c) = -4°C

Change in temperature is T_f-T_i = -4-24 = -28°C

∴ Rate of Reduction = \(\frac{\text { change in temperature }}{\text { Time }}\)

= \(\frac{-28}{7}\)

= -4°c/hour.

∴ The rate of reduction of temperature per hour is 4°C

WBBSE Class 7 Algebra Exercise Solutions

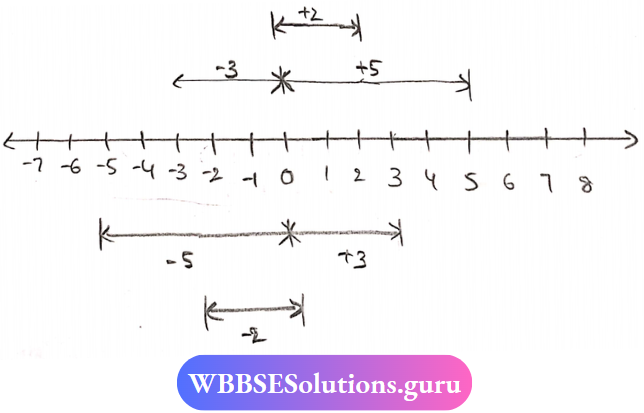
Question 8. Draw a number line and verify with examples that the commutative law of Subtraction does not hold.
Solution:

Let us take a simple example

1. 5-3=2 and also
2. 3-5=-2

These results are not the same.

∴ The commutative law of Subtraction does not hold true for these numbers.

Question 9. By what number should be added to ((-5)x(4)-(+3) to get the number [{(-12) (-3)}x (-2)]
Solution:

⇒ [{(-12) ÷ (-3)} x (-2)] – {(5)x(4)-(+3)}

⇒ [{\(\frac{-12}{-3}\) x(-2)] – {(20-3)}

⇒ [4 x (2)] – (17)

⇒ -8-17

⇒ -25

∴ {(-5)× (4) −(+3)} to get the number [{(-12) ÷ (-3)} × (-2)] is -25

Algebra Formulas For Class 7 WBBSE

Question 10. Find the value of [720÷ (21+3) ÷ (-6) x 5] ÷ (-25)  
Solution:

⇒ \([720 \div(21+3) \div(-6) \times 5] \div(-25)\)

⇒ \([720 \div(24) \div(-30)] \div(-25)\)

⇒ \(\left[\frac{\frac{720}{24}}{(-30)}\right] \div(-2.5)\)

⇒ \(\left[\frac{720}{24} \times \frac{1}{(-30)}\right] \div(-25)\)

⇒ \(\left(\frac{720}{-720}\right) \div(-25)\)

⇒ \((-1) \div(-25)\)

⇒ \(\frac{+1}{+25}\)

∴ 0.04

∴ \([720 \div(21+3) \div(-6) \times 5] \div(-25)=0.04\)