WBBSE Class 7 Maths Solutions For Algebra Chapter 4 Algebraic Operations

Algebra Chapter 4 Algebraic Operations

Question 1. Choose the correct answer.

1. Sum of x²y – 3xy and 7xy² is

1. 7xy² + 2x²y
2. 7xy² – 2x²y
3. 5x²y
4. 8xy² – 3x²y

Solution:

x²y – 3x²y and 7xy²

⇒ 7xy² – 2x²y

∴ (x²y-3x²y) and 7xy² = 7xy² -2x²y

Option (2) 7xy² – 2x²y is the correct answer.

Read and Learn More Class 7 Maths Solutions

WBBSE Class 7 Algebra Chapter 4

2. The numerical co-efficient of the term -3x²+5x-7 other than the constant term is

1. (-3,5)
2. (-3,5,-7)
3. (5, -7)
4. (-3,-7)

Solution: -3x² + 5x -7

The numerical coefficient of the term (-3,5)

∴ Option (1) (3,5) is the correct answer,

3. The product of (5abc) and (-3abc) is

1. -15a⁸b¹²c¹⁰
2. 15 a⁶b⁷c⁷
3. -15 a⁶b⁷c⁷
4. 15 a⁸b¹²c¹⁰

Solution:

⇒ \(\left(5 a^4 b^3 c^2\right) \text { and }\left(-3 a^2 b^4 c^5\right)\)

⇒ \(\left(5 a^4 b^3 c^2\right) \times\left(-3 a^2 b^4 c^5\right)\)

⇒ \(5 a^4 \times\left(-3 a^2\right) \times b^3 \times b^4 \times c^2 \times c^5\)

⇒ \(-15 a^6 b^7 c^7\)

⇒ \(\left(5 a^4 b^3 c^2\right) \text { and }\left(-3 a^2 b^4 c^5\right)=-15 a^6 b^7 c^7\)

∴ Option (3) \(-15 a^6 b^7 c^7\) is the correct Answer.

Class 7 Maths Algebra Solutions WBBSE

4. The value of \(\frac{(-8 y) \div(4 z)}{4}\) is

1. -8yz
2. -16yz
3. \(\frac{2z}{y}\)
4. \(\frac{-y}{2z}\)

Solution:

⇒ \(\frac{(-8 y) \div(4 z)}{4}\)

⇒ \(\frac{\frac{-8 y}{4 z}}{4}\)

⇒ \(\frac{-8 y}{4 z} \times \frac{1}{4}\)

⇒ \(\frac{-8 y}{\frac{16 z}{2}}\)

⇒ \(\frac{-y}{2 z}\)

∴ \(\frac{(-8 y) \div(4 z)}{4}=\frac{-y}{2 z}\)

∴ Option (4) \(\frac{-y}{2 z}\) is correct answer.

Question 2. Write true or False:

1. a ÷ b of c = a ÷ b x c
2. a (b x c) = ab x ac
3. If the HFC of a and b is c then their LCM is \(\frac{ab}{c}\)

Solution:

1. a ÷ b of c = a ÷ b x c → False
2. a (b x c) = ab x ac → False
3. If the HFC of a and b is then their LCM is \(\frac{ab}{c}\) → True

Question 3. Fill in the blanks.

1. The value of a^x-y x a^y-z x a^z-x is _______
2. The sum of numerical coefficients of the term \(-\frac{1}{2} x^2, \frac{3}{4} y^2, \frac{1}{4} z^2 \text { and }-\frac{5}{2} x y\) is _______
3. The Subtraction of (5x² -4xy-y²) from O is ______

Solution:

1. \(a^{x-y} \times a^{y-z} \times a^{z-x}\)

⇒ \(a^{x-y+y-z+z+x} \quad a^m \times a^n \times a^0=a^{m+n+0}\)

⇒ \(a^{\prime}=0\)

⇒ \(a^{x-y} \times a^{y-z} \times a^{z-x}=0\)

2. The Sum of numerical coefficients of the term \(-\frac{1}{2} x^2, \frac{3}{4} x^2, \frac{1}{4} z^2\) and \(-\frac{5}{2} x y\) is

⇒ \(-\frac{1}{2}+\frac{3}{4}+\frac{1}{4}+\left(-\frac{5}{2}\right)\)

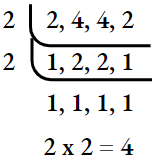
⇒ \(\frac{-2+3+1-10}{4}\)

⇒ \(\frac{-12+4}{4}\)

⇒ \(2 \times 2=4\)

∴ \(\frac{-8}{4}\)

∴ -2

∴ \(-\frac{1}{2} x^2, \frac{3}{4} y^2, \frac{1}{4} z^2 \text { and }-\frac{5}{2} x y=-2\)

3. The Subtraction of (5x²-4xy-y²) from 0 is

⇒ 0-(5x²-4xy-y²)

⇒ -5x² + 4ху + y²

∴ -5x² + 4xy + y²

WBBSE Class 7 Maths Chapter 4 Answers

Question 4. Identify the like terms. -a²b, 7ab², 1/2a²b, 5/2ab, 7a²b
Solution:

Like terms = -a²b, 7a²b, 1/2 a²b.

Question 5. Find the numerical coefficient of the terms other than the constant term.

1. 3x² – 5xy + 7
2. x – 3xy + 7y² – 6
3. \(\frac{5x^3}{7}\) + 4x – 8

Solution:

1. 3x² – 5xy + 7

The numerical coefficients are (3,-5).

2. x – 3xy + 7y² – 6

The numerical coefficients are (1,-3, +7)

3. \(\frac{5x^3}{7}\) + 4x – 8

The numerical coefficient is (5/7,4)

Question 6. Represent the following algebraic expressions into a factor tree type of figure mentioning the prime factors of each term.

1. 7x
2. 3y²+27+5

Solution:

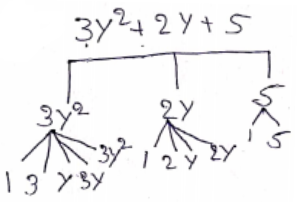
WBBSE Class 7 Algebra Exercise Solutions

Question 7. How much must be added to (x² – 7x + 8) to get (3x² + 8x – 9)
Solution:

(x² +7x +8) to get (3x² + 8x -9)

(3x² + 8x-9) – (x² – 7x + 8)

3x² + 8x – 9 – x² + 7x – 8

2x² + 15x – 17

∴ 2x² + 15x – 17 must be added to (x² – 7x + 8) to get (3x² + 8x – 9).

Question 8. Multiply

1. (5x – 7y) (5x + 7y)
2. \(\left(-\frac{2}{3} a^2 b c^2\right) \times\left(\frac{7}{2} a b^5 c^5\right) \times\left(\frac{3}{7} a^3 b c^4\right)\)

Solution:

1. (5x – 7y)(5x + 7y)

Here a = 5, b = 7y

⇒ (5x)² – (7y)²

⇒ 25x² – 49y²

∴ (5x-7y)(5x+7y) = 25x² – 49y²

2. \(\left(-\frac{2}{3} a^2 b c^2\right) \times\left(\frac{7}{2} a b^5 c^5\right) \times\left(\frac{3}{7} a^3 b c^4\right)\)

⇒ \(-\left(\frac{2}{3} \times \frac{7}{2} \times \frac{3}{7}\right) \times\left(a^2 b c^2\right) \times\left(a b^5 c^5\right) \times\left(a^3 b c^4\right)\)

⇒ \(-\left(a^{2+1+3} \cdot b^{1+5+1} \cdot c^{2+5+4}\right)\)

⇒ \(-\left(a^6 \cdot b^7 \cdot c^{11}\right)\)

∴ \(\left(-\frac{2}{3} a^2 b c^2\right) \times\left(\frac{7}{2} a b^5 c^5\right) \times\left(\frac{3}{7} a^3 b c^4\right)=-\left(a^6 \cdot b^7 \cdot c^{11}\right)\)

Question 9. Divide:

1. \(\left(22 x^5-11 x^3+33 x^2 y\right)\) by \(11 x^4\)
2. \(169 a^2 b c^4-52 a b^4 c^5-78 a^3 b^3 c^3 b y-13 a b c^4\)

Solution:

1. \(\left(22 x^5-11 x^3+33 x^2 y\right)\) by \(11 x^4\)

⇒ \(\frac{22 x^5}{11x^3}-\frac{11 x^4}{11 x^4}+\frac{33 x^2 y}{11 x^4}\)

⇒ \(2 x-\frac{1}{x}+\frac{3 y}{x^2}\)

∴ \(\left(22 x^5-11 x^3+33 x^2 y\right) \text { by } 11 x^4\) = \(2 x-\frac{1}{x}+\frac{3 y}{x^2}\)

2. \(169 a^2 b c^4-52 a b^4 c^5-78 a^3 b^3 c^3 b y-13 a b c^4\)

⇒ \(\frac{169 a^2 bc^4}{-13 a b c^4}-\frac{52 a b^4 c^5}{-13 a b c^4}-\frac{78 a^3 b^3 c^3}{-13 a b c^4}\)

⇒ \(-13 a+4 b^3 c+6 a^2 b^2 c^{-1}\)

⇒ \(-13 a+4 b^3 c+\frac{6 a^2 b^2}{c^-1}\)

∴ \(169 a^2 b c^4-52 a b^4 c^5-78 a^3 b^3 c^3 by -13 a b c^4\) is \(-13 a+4 b^3 c+\frac{6 a^2 b^2}{c}\)

Class 7 Algebra Problems With Solutions

Question 10. If the perimeter of an isosceles triangle is (3a-4b+5c) cm and the length of its base is (a+2b-c)cm then Find the length of the other sides.
Solution:

Given Data, Isosceles Triangle

Perimeter = (3a-4b+5c)cm

Base length = (a+2b-c)cm

length of other sides =?

In the Isoceles Triangle two sides are equal in length

perimeter = 2a+b; a = side , b = base

(3a-4b+5c) = 2a +(a+2b-c)

(3a-4b+5c) – (a+2b-c) = 2a

3a – 4b + 5c – a – 2b + c = 2a

3a – a – 4b -2b + 5c + c = 2a

2a – 6b + 6c = 2a

2(a-3b+3c) = 2a

∴ Length of other sides are a = (a-3b+3c) cm

Question 11. Simplify

1. \(\frac{a-b}{a b}+\frac{b-c}{b c}+\frac{c-a}{c a}\)
Solution:

⇒ \(\frac{a-b}{a b}+\frac{b-c}{b c}+\frac{c-a}{c a}\)

⇒ \(\frac{c(a-b)+a(b-c)+b(c-a)}{a b c}\)

⇒ \(\frac{a c-b c+a b-ac c+b c-a b}{a b c}\)

⇒ \(\frac{1}{a b c}\)

∴ \(\frac{a-b}{a b}+\frac{b-c}{b c}+\frac{c-a}{c a}=\frac{1}{a b c}\)

2. \((x-5)\left(x^2+5 x+25\right)+(2 x-1)\left(4 x^2+2 x+1\right)-(3 x-2)\left(9 x^2+6 x+4\right)\)
Solution:

⇒ \(x^3+5 x^2+25 x-5 x^2-25 x-125+8 x^3+4 x^2+2 x-4 x^2-2 x-1\)–\((27 x^3+18 x^2+12 x-18 x^2-12 x-8)\)

⇒ \(x^3+8 x^3-27 x^3+5 x^2-5 x^2+4 x^2-4 x^2\)–\(18 x^2+18 x^2+25 x-25 x+2 x-2 x+12 x-12 x-125-1+18\)

∴ \(-18 x^3-118\)

3. (a – b)(b – 2c + a)+ (b – c)(c – 2a + b) + (c – a) (a – 2b + c)
Solution:

⇒ (a – b)(b – 2c + a)+ (b – c)(c – 2a + b) + (c – a) (a – 2b + c)

⇒ ab-2ac+a²-b²+2bc-ab+bc-2ab+b²-c²+2ac-bc+ac-2bc+c²-a²+2ab-ac

∴ (a-b) (b-2c+a)+(b-c)(c-2a+b) + (c-a)(a-2b+c) = 0

Class 7 Maths Chapter 4 Solved Exercises

Question 12. If A = 2x+3y-4z; B = 2y+3x-4z and C = 2z + 3x – 4y then find the value of (A-2B-3C)
Solution:

Given that.

A = 2x+3y-4z

B = 2y+3x-4z

C = 2z+3x-4y

(A-2B-3c) = {(2x+3y-4z) – 2(2x+3x-4z)-3(2z +3x-4y)}

= {(2x+3y-4z)-4y-6x+8z-6z-9x+12y}

= (2x+3x-4z-4y-6x+8z-6z-9x+12y)

= (2x-6y-9x + 3y – 4y + 12y -4z + 8z – 62)

(A-2B-3C) = (-13x + 11y – 2z)