Arithmetic Chapter 2 Compound Interest And Uniform Rate Of Increase Or Decrease
Money is said to be lent at compound interest if the interest at the end of the year or a fixed period of time in added to the principal, and thus the amount obtained becomes the new principal for the next period and so on.
Important points to be remembered:
- For interest is calculated per annum i.e. time period is 1; compound interest is equal to simple interest.
- Compound interest for more than 1 year is always greater than simple interest (or for any time period, the same result will occur for more than 1 time period).
Important results: If R be the rate of interest per annum, T is the duration in years, A is the amount and P is the principal.
Read and Learn More WBBSE Solutions for Class 10 Maths
1. If interest is compounded annually, then—
- \(A=P\left(1+\frac{R}{100}\right)^T\)
- \(P=\frac{A}{\left(1+\frac{R}{100}\right)^T}\)
If interest is compounded half yearly, then (i.e. time period = \(\frac{12}{6}\) = 2)
\(A=P\left(1+\frac{\frac{\mathrm{R}}{2}}{100}\right)^{2 T}\)If interest is compounded quarterly, then [time period \(\frac{12}{3}\) = 4]
\(A=P\left(1+\frac{\frac{R}{4}}{100}\right)^T\)If rate of interest is R,%, R2%, R3% respeclively, for 1st, 2nd and 3rd years then
\(A=P\left[\left(1+\frac{R_1}{100}\right)\left(1+\frac{R_2}{100}\right)\left(1+\frac{R_3}{100}\right)\right]\)
2. Compound interest = A- P
3. If a sum becomes x times in y years, then after xy years it will be (x)y times.
4. It a certain sum becomes n times in T years, then rate of interest is
\(R=100\left[(n)^{\frac{1}{T}}-1\right]\)Class 10 Maths Arithmetic Chapter 2 Solutions
5. Relation between simple interest and compound interest
Simple interest = \(\frac{\mathrm{R} \times \mathrm{T}}{100\left[\left(1+\frac{\mathrm{R}}{100}\right)^{\mathrm{T}}-1\right]} \times \mathrm{C} \cdot \mathrm{I}\)
6. Difference between compound interest and simple interest.
Compound interest- simple interest = \(P\left[\left(\frac{100+R}{100}\right)^T-\frac{R T}{100}-1\right]\)
Rate of growth and depreciation: Some basic terms:
- Growth: An increase in price or population or learners, production to any concerning time uniformly is called growth or appreciation.
- Similarly the rate decrease, uniformly concerning the time (fall of efficiency of a Machine, decrease valuation of old building, furniture, movable properties, or any) is called a uniform rate of decrease or depreciation.
Important result:
1. If the original value is P., the final value is A, the rate of growth is R% per annum and the period is T years then
For growth
1. \(A=P\left(1+\frac{R}{100}\right)^T\)
2. Increase = A – P
For depreciation
1. \(A=P\left(1-\frac{R}{100}\right) T\)
2. decrease = A – P
2. 1. If A > P, there is an increase
2 . If A < P, there is a decrease
Geometric Progression Class 10 Solutions
Arithmetic Chapter 2 Compound Interest And Uniform Rate Of Increase Or Decrease True Or False
Example 1. In 2 years the simple interest and compound interest of a certain sum of money on a particular rate will be equal.
Solution: False
Example 2. The amount of simple interest is less than compound interest in 1 year when the principal and the rate of interest be equal.
Solution: False
Example 3. Amal borrowed Rs. P at 10% per annum simple interest and Bimal borrowed Rs. p at 10% compound interest per annum for 2 years. Bimal have to pay more than Amal to settle their loan.
Solution: True
Example 4. If P be the price of a building. It’s value decreases r% every year. The value of the building at the end of 2 years will be \(P\left(1-\frac{r}{100}\right)^2\)
Solution: True
Example 5. The formula I = \(\frac{p r t}{100}\) is used to calculating compound interest.
Solution: False
Example 6. The formula \(\mathrm{A}=\mathrm{P}\left(1-\frac{r}{100}\right)^n\) is used to find compound interest.
Solution: False
Class 10 Arithmetic Chapter 2 Solved Examples
Example 7. Compound interest will be always less than Simple Interest for some money at fixed rate of interest for a fixed time.
Solution: False
Example 8. In case of compound interest is to be added to the principal at the fixed time interval, i.e. the amount of principal increases continuously.
Solution: True
Example 9. The simple interest for the 1st year is the same as the compound interest (compounded annually) for the first year.
Solution: True
Example 10. If interest is compounded monthly, the formula for amount in compound interest is \(A=P\left(1+\frac{\frac{r}{12}}{100}\right)^{12 n}\)
Solution: True
Arithmetic Chapter 2 Compound Interest And Uniform Rate Of Increase Or Decrease Fill In The Blanks
Example 1. The formula to find the uniform rate of increase and compound interest are _______
Solution: Same
Example 2. On a certain sum of money at the same rate of simple interest and compound interest, the amount of interest receivable is equal for_______ years.
Solution: 1st
Example 3. The compound interest on Rs. 1000 for 2 years at 10% per annum is ₹ _______
Solution: Rs. 210
Wbbse Class 10 Arithmetic Notes
Example 4. The rate of depreciation of a machine is 10% per annum two years ago the price of the machine was Rs. _______ when the present price of that machine is Rs. 500.
Solution: 405
Example 5. The compound interest and simple interest for one year at the fixed rate of interest oh fixed sum to money are______
Solution: Same
Example 6. If something are increased by fixed rate with respect time that is ______
Solution: Uniform rate
Example 7. If some things are decreased by a fixed rate with respect to time this is a uniform rate of ______
Solution: Decrease
Example 8. At 8% compound interest per annum Rs 10,000 amounts to Rs. 11664 in ____ years.
Solution: 2
Arithmetic Chapter 2 Compound Interest And Uniform Rate Of Increase Or Decrease Short Answer Type Questions
Example 1. Let us write the rate of compound interest per annum so that this amount on ₹ 400 for 2 years becomes 441.
Solution: \(A=P\left(1+\frac{r}{100}\right)^n\)
or, \(441=400\left(1+\frac{r}{100}\right)^2\)
or, \(\frac{441}{400}=\left(1+\frac{r}{100}\right)^2\)
or, \(\quad\left(1+\frac{r}{100}\right)^2=\left(\frac{21}{20}\right)^2\)
or, \(1+\frac{r}{100}=\frac{21}{20}\)
or, \(\quad \frac{r}{100}=\frac{21}{20}-1\)
or, \(\quad \frac{r}{100}=\frac{1}{20}\)
or, r=5
∴ Rate of interest in 5% per annum.
Example 2. If a sum of money doubles it self at compound interest in n years, let us write in how many years will it become four times.
Solution: \(2 \mathrm{P}=\mathrm{P}\left(1+\frac{r}{100}\right)^n\)
or, \(2=\left(1+\frac{r}{100}\right)^n\)
Now. let it become four times is T years.
\(4 P=P\left(1+\frac{r}{100}\right)^{\mathrm{T}}\)or, \(4=\left(1+\frac{r}{100}\right)^{\mathrm{T}} \quad \text { or, }\left(1+\frac{r}{100}\right)^{2 n}=\left(1+\frac{r}{100}\right)^{\mathrm{T}}\)
∴ T = 2n; Required time is 2n years.
Example 3. Let us calculate the principle that at the rate of 5% compound interest per annum becomes ₹ 615 after 2 years.
Solution: \(\mathrm{P}=\left(1+\frac{r}{100}\right)^n\)

∴ P = ₹ 6000.
∴ 5% compound interest per annum becomes ₹ 615 after 2 years is ₹ 6000.
Example 4. The price of a machine depreciate at the rate of r% per annum let us find the price of the machine that was n years before.
Solution: \(P_1=\mathrm{P}\left(1-\frac{r}{100}\right)^n\)
or, \(P=A\left(1-\frac{r}{100}\right)^{-n}\)
∴ Required price = ₹ \(A\left(1-\frac{r}{100}\right)^{-n}\)
The price of the machine that was n years before ₹ \(A\left(1-\frac{r}{100}\right)^{-n}\)
Geometric Progression Formulas Class 10
Example 5. The price of a machine depreciates at the rate of \(\frac{r}{2}\) %.per annum. Let us find the price of the machine that was 2n years before.
Solution: \(\mathrm{A}=\mathrm{P}\left(1-\frac{\frac{r}{2}}{100}\right)^{2 n}=\mathrm{P}\left(1-\frac{r}{200}\right)^{2 n}\)
∴ \(\mathrm{P}=\mathrm{A}\left(1-\frac{r}{200}\right)^{-2 n}\)
∴ required price = ₹ \(\mathrm{A}\left(1-\frac{r}{200}\right)^{-2 n}\)
∴ The price of the machine that was 2n years before ₹ \(\mathrm{A}\left(1-\frac{r}{200}\right)^{-2 n}\)
Example 6. If the rate of increase in population is r% per annum the population after n years is p, let us find the population that was n years before.
Solution: \(\mathrm{P}=x\left(1+\frac{r}{100}\right)^n\)
∴ \(x=\mathrm{P}\left(1+\frac{r}{100}\right)^{-n}\)
∴ Population was \(P\left(1+\frac{r}{100}\right)^{-n}\)
Example 7. A certain sum of money invested at 4% per annum compounded semi-annually amounts to Rs 7803 at the end of 2 years find the sum.
Solution: \(\mathrm{A}=\mathrm{P}\left(1+\frac{r}{100}\right)^n\)

or, 7803 = \(P\left(1+\frac{1}{50}\right)^2 \quad \text { or, } \quad P=\frac{7803 \times 50 \times 50}{51 \times 51}=7500\)
∴ The sum invested is 7500.
Example 8. Find the effective rate when nominal rate is 8% compounded quarterly.
Solution: Effective rate = \(\left(1+\frac{8}{400}\right)^4-1=(1+0 \cdot 02)^4-1\)
= 1.0824 – 1 = .0824 = 8.24%
[If the given (nominal) rate of interest is R% and the interest compounded n times in the effective rate of interest = \(\left(1+\frac{\mathrm{R}}{100 n}\right)^n-1\)]
Example 9. Find the amount on Rs. 3000 at 10% compound interest per annum for 2 years.
Solution: \(A=P\left(1+\frac{r}{100}\right)^n\)

= Rs. 3630
10% compound interest per annum for 2 years is Rs. 3630
Geometric Progression Formulas Class 10
Example 10. What is the difference between simple interest & compound interest on 7 8000 at 10% for 2 years.
Solution:
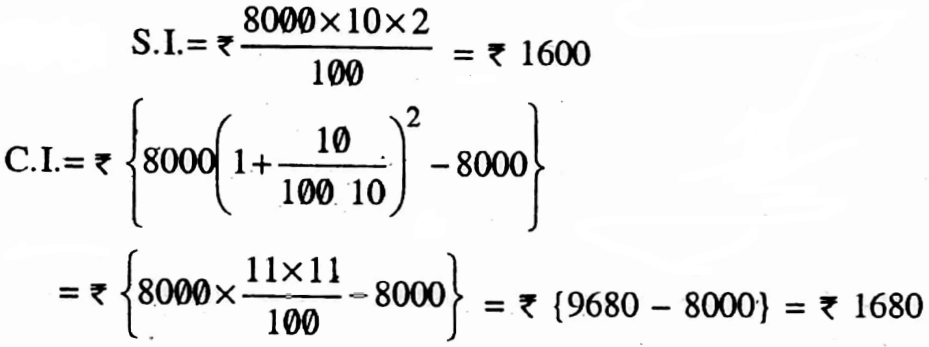
∴ Difference = ₹ (1680 – 1600) = ₹ 80
Example 11. The population of a town increases every year by 5%. If the present population is 48000 then what will be the population of the town in the next 2 years?
Solution:

∴ The population will be 52920.
∴ The population of the town in the next 2 years is 52920.
