WBBSE Solutions For Class 10 Maths Geometry Chapter 1 Theorems Related To Circle

Geometry Chapter 1 Theorems Related To Circle

⇔ Circle Definition: A circle is the locus of a point which moves in a plane in such a way that its distance from a given fixed point in the plane is always constant.

⇒ The fixed point is called the centre and the given constant distance is called the radius of the circle.

WBBSE Notes For Class 10 Geography And Environment	WBBSE Notes For Class 10 History And Environment
WBBSE Solutions For Class 10 Life Science	WBBSE Class 10 Life Science Multiple Choice Questions
WBBSE Solutions for Class 10 Maths	WBBSE Class 10 Maths Multiple Choice Questions
WBBSE Notes For Class 10 Physical Science And Environment

 

⇒ O is centre and OA is the radius of circle.

⇔ Chord Definition:  A line segment joining any two points on a circle is called a chord or a circle.

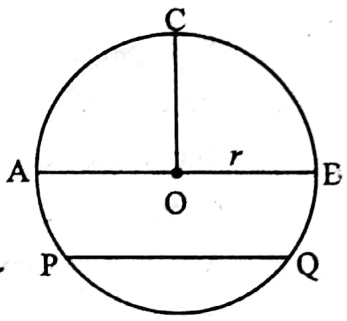
⇒ PQ is the chord of a circle of centre O.

⇔ Diameter Definition:  A chord passing through the centre is known as its diameter.

⇒ AB is the diameter of the circle.

⇔ Arc Definition: The part of the circle is called Arc.

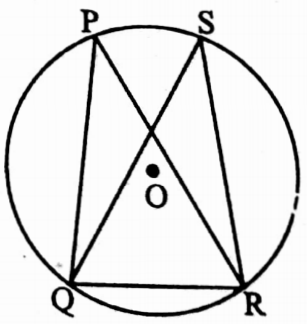
⇒ The greater arc is called Major Arc and Smaller arc is called Minor Arc.

Read and Learn More WBBSE Solutions for Class 10 Maths

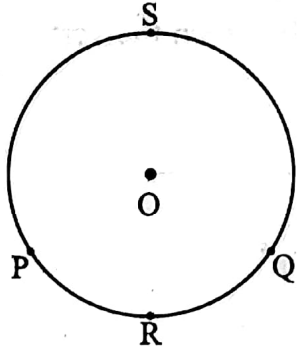
⇒ Major Arc is \(\overparen{\mathrm{PSQ}}\) and Minor Arc is \(\overparen{\mathrm{PRQ}}\).

⇔ Semicircle Definition:  A diameter of a circle divides it into two equal parts which are arcs. Each of these two arcs is called a semi-circle.

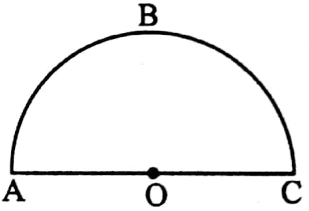
⇒ \(\overparen{\mathrm{ABC}}\) is the semi circle.

Class 10 Maths Geometry Chapter 1 Solutions

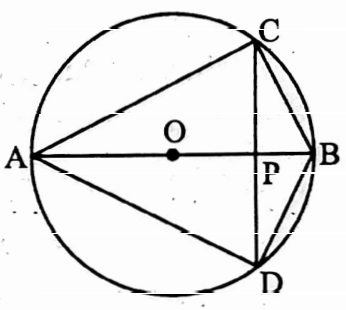
⇔ Segment of a circle Definition:  The chord of a circle divides the circular region into two parts. Each of the parts is called a segment.

 

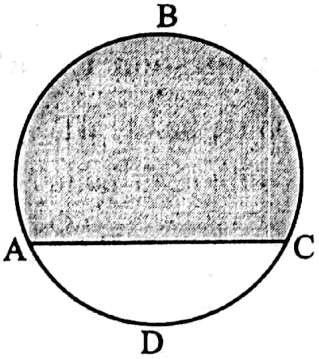
⇒ The greater segment is Major segment and the Smaller segment is Minor segment.

⇒ The region ABC is Major segment and the region ADC is Minor segment.

⇔ Concentric circles Definition: Circles having the same centre but with different radii are said to be concentric circles.

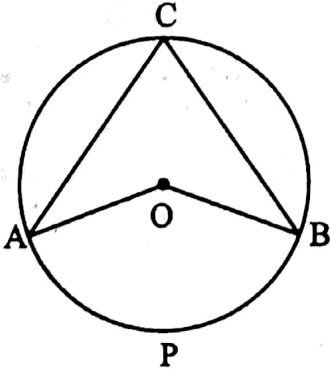
⇒ ∠ACB is called the front angle by the circular arc \(\overparen{\mathrm{APB}}\) and ∠AOB is called the angle at the centre O which is made by the arc \(\overparen{\mathrm{APB}}\).

Theorems related to circle:

1. In the same circle or in equal circles, equal chords intercept equal angles at the centre.
2. In the same circle or in equal circles, the chords which subtend equal angles at the centre are equal.
3. One and only one circle can be drawn through three non-collinear points.
4. If a line drawn from the centre of any circle bisects the chord, which is not a diameter, will be perpendicular on the chord.
5. A perpendicular is drawn from the centre of a circle on a chord, which in not a diameter, and bisects the chord.
6. The angle subtended at the centre by an arc is twice that of an angle subtended in the circle.
7. In any circle angles in the same segment are equal.
8. The angle in a semicircle is a right angle.
9. If a straight line segment makes equal angles at the two points situated on the same side of it, then the four points are concyclic.
10. The opposite angles of a cyclic quadrilateral are supplementary to each other.
11. If the opposite angles of q quadrilateral are supplementary to each other, then the vertices of the quadrilateral are concyclic. [In case of asterisk marks proofs are not necessary.]

Basic Geometrical Concepts Class 10 Solutions

Geometry Chapter 1 Theorems Related To Circle True Or False

Example 1. Only one circle can be drawn through three collinear points.

Solution: Only one circle can be drawn through three non-collinear points.

∴ the statement is false.

Example 2. The two circles ABCDA and ABCEA are same circle.

Solution: Clearly the statement is true

Example 3. If two chords AB and AC of a circle with its centre O are situated on the opposite sides of the radius OA, then ∠OAB = ∠OAC.

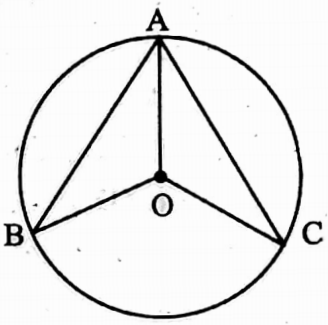
Solution: If AB = AC then ∠OAB = ∠OAC

∴ the statement is false

Example 4. If O is the centre of the circle, then ∠AOB = 2∠ACD

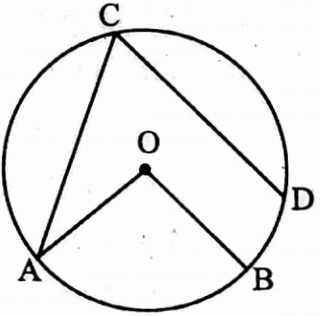
Solution: Since the angle ∠AOB is at the centre of the circle formed by circular arc AB and ∠ACD is on the circle formed by circular arc ABD of a circle with centre O,

∴ ∠AOB ≠ 2 ∠ACD

∴ The statement is false.

Class 10 Geometry Chapter 1 Solved Examples

Example 5. Point O lies within the triangular region ABC in such a way that OA = OB and ∠AOB = 2 ∠ACB. If we draw a circle with centre O and length of radius OA, then the point C lies on the circle.

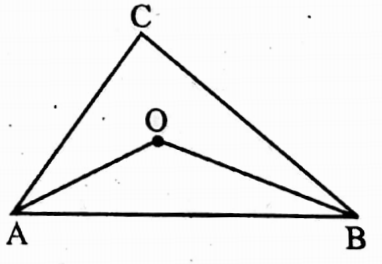
Solution: as OA = OB

∴ If we drew a circle with centre O and radius OA, then the circle passes through the point B.

∴ The angle ∠AOB is at the centre O formed by a circular arc AB.

Again ∠AOB = 2 ∠ACB

∴ ∠ACB is the angle on the circle formed by circular arc AB

∴the point C lies on the circle.

∴ The statement is true

Example 6. AD and BE are the perpendiculars on side BC and CA of the triangle ABC. A, B, D, and E are concyclic.

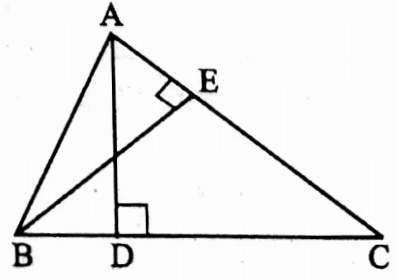
Solution: ∠AEB = ∠ADB = 90°

as a line segment AB joining two points A and B subtends equal angles at two other points D and E on the same side of AB.

∴ A, B, D, and E points are concyclic.

∴ The statement is true

Example 7. In ΔABC, AB = AC, BE and CF are the bisectors of the angles ∠ABC and ∠ACB and they intersect AC and AB at the points E and F respectively. Four points B, C, E, F are not concyclic.

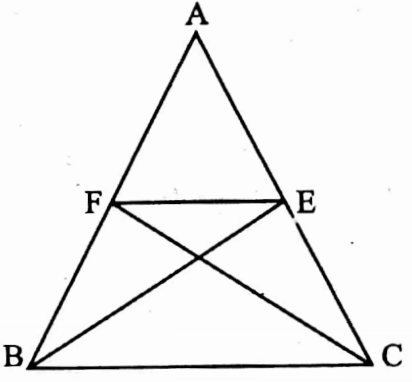
Solution: Join E, F

⇒ InΔABC, AB = AC

⇒ ∠ACB = ∠ABC

⇒ or, \(\frac{1}{2}\) ∠ACB = \(\frac{1}{2}\) ∠ABC

∴ ∠ECF = ∠EBF

⇒ as line segment BC joining two points B and C subtends equal angle at two other points E and F on the same side BC

⇒ B, C, E, and F points are concyclic.

∴ The statement is false.

Example 8. The angle in the segment of a circle which is greater than a semicircle is an obtuse angle.

Solution: Clearly statement is false.

Example 9. O is the midpoint of the side AB of the triangle ABC, and OA = OB = OC ; if we draw a circle with side AB as diameter, the circle passes through the point C.

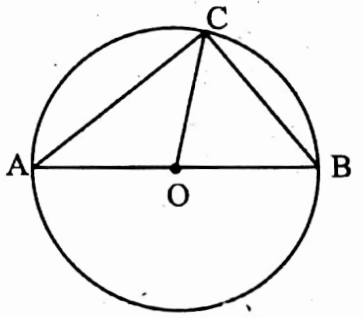
Solution: As OA = OB = OC,

∴ The statement is true.

Geometry Theorems Class 10 Solutions

Example 10. The opposite angle of a cyclic quadrilateral is complimentary.

Solution: The statement is false.

Example 11. If any side of a cyclic quadrilateral be produced the exterior angle so formed is equal to the interior opposite angle.

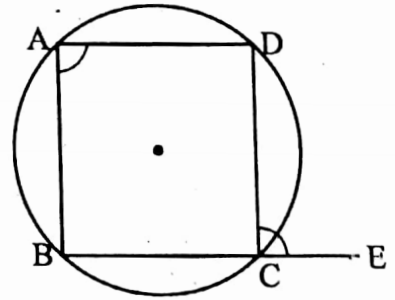
Solution: The statement is true.

Geometry Chapter 1 Theorems Related To Circle Fill In The Blanks

Example 1. If the ratio of two chords PQ and RS of a circle with its centre O is 1 : 1, then, ∠POQ: ∠ROS = _________

Solution:

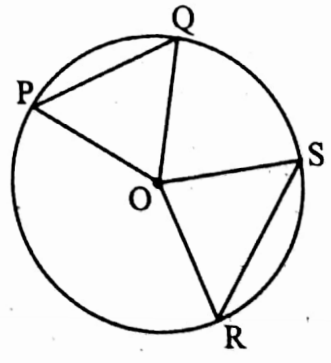
Ratio of length of chord PQ and RS of a circle with its centre O is 1: 1

∴ PQ = RS

∴ ∠POQ = ∴ ∠ROS

∠POQ : ∠ROS =1:1

∴ 1: 1

Example 2. The perpendicular bisector of any chord of a circle is ________ of that circle

Solution:

∴ Passes through centre.

Example 3. The angle at the centre is ________ the angle on the circle, subtended by the same arc.

Solution: Double.

Example 4. The length of two chord AB and AC are equal of a circle with centre O. If ∠APB and∠AQC are angles on the circle, then the value of the two angles are_______

Solution:

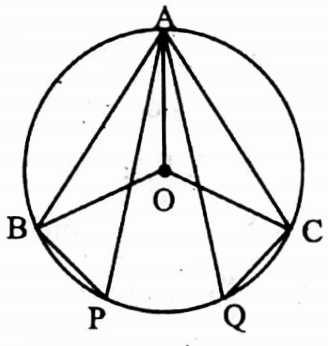
join O, A; O, B and O, C.

⇒ As AB = AC, ∴ ∠AOB = ∠AOC

⇒ ∠AOB = 2 ∠APB and ∠AOC = 2 ∠AQC

∴ 2 ∠APB = 2 ∠AQC

⇒ or, ∠APB = ∠AQC

∴ Equal.

Example 5. All angles in the same segments are ________

Solution: Equal

Example 6. If the line segment joining two points subtends equal at two other points on the same side, then the four points are ________

Solution: Concyclic

Class 10 Maths Geometry Important Questions

Example 7. If two angles on the circle formed by two arcs are equal then the lengths of arcs are __________

Solution: Equal

Example 8. The semicircular angle is ______

Solution: Right angle.

Example 9. The angle in the segment of a circle which is less than a semicircle is an ______ angle.

Solution: obtuse

Example 10. The circle drawn with a hypotenuse of a right-angled triangle as diameter passes through the _______

Solution: Right angular vertex.

Example 11. If the opposite angles of a quadrilateral be supplementary then the vertices of the quadrilateral will be ______

Solution: Concyclic

Class 10 Maths Geometry Chapter 1 Solutions

Example 12. A cyclic parallelogram is a ______ picture.

Solution: Rectangular.

Example 13. The vertics of square is __________

Solution: Concyclic.

Geometry Chapter 1 Theorems Related To Circle Short Answer Type Question

Example 1. Two equal circles of radius 10 cm. intersect each other and the length of their common cord is 12 cm. Determine the distance between the two centres of two circles.

Solution:

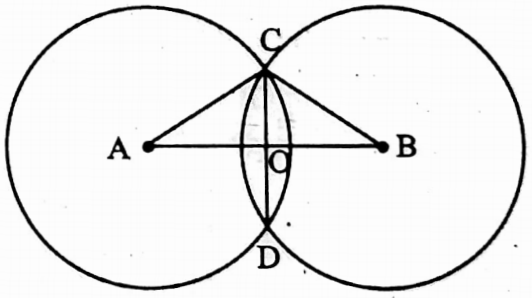
⇒  Let AC and BC are the radius of two circles of centres A and B respectively.

∴ AC = BC = 10 cm their common chord is CD where CD = 12 cm AB and CD intersect at O;

∴ OC = OD = \(\frac{1}{2}\) x 12 cm = 6 cm

⇒  and ∠AOC = ∠BOC = 90°

⇒ In ΔAOC, OA² + OC² = AC² [From pythagorus theorem]

⇒ OA² + 6²  = 10²

⇒ or, OA = \(\sqrt{100-36}\)cm = √64 cm = 8 cm

⇒ Similarly, OB = 8 cm

∴ AB = (8 + 8) cm = 16 cm.

Basic Geometrical Concepts Class 10 Solutions

Example 2. AB and AC are two equal chords of a circle having the radius of 5 cm. The centre of the circle situated at the outside of the triangle ABC. If AB = AC = 6 cm, then calculate the length of the chord BC.

Solution:

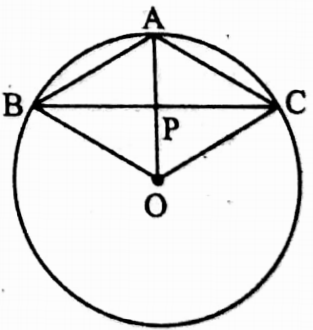
⇒  OA = OB = OC = 5 cm

⇒  OA and BC intersect at P,

⇒  Let OP = x cm, AP = (5 – x) cm

⇒  In ΔAOB and ΔAOC,

⇒  AB = AC, OB = OC and OA common side

∴ ΔAOB = ΔAOC [By SSS axiom of congruency]

∴ ∠BAO = ∠CAO

⇒  i.e. ∠BAP = ∠CAP

⇒ In ΔBAP and ΔCAP,

⇒ AB = AC, ∠BAP = ∠CAP and AP = AP (common side)

∴ ΔBAP ≅ ΔCAP [By SAS axiom of congruency]

∴ ∠APB = ∠APC = \(\frac{180^{\circ}}{2}\) =90°

∴ AP ⊥ BC

∴ BP = CP [The perpendicular drawn to a chord, which is not a diameter, from the centre of the circle, bisects the chord]

In ΔABP, ∠APB = 90°

AP² + BP² = AB²

(5 – x)² + BP² = 6²

⇒ BP² = 36 – (5 – x)²

In ΔBOP, OP² + BP² = OB²

x² + BP² = 5²

⇒ BP² = 25 – x²

∴ 36 – (5 – x)² = 25 – x²

⇒ 36 – 25 + 10x – x² = 25 – x²

⇒ 10x = 14

⇒ x = \(\frac{7}{5}\)

\(\mathrm{BP}^2=\left\{25-\left(\frac{7}{5}\right)^2\right\} \mathrm{cm}^2=\left(25-\frac{49}{25}\right) \mathrm{cm}^2=\frac{576}{25} \mathrm{~cm}^2\) \(\mathrm{BP}=\sqrt{\frac{576}{25}} \mathrm{~cm}=\frac{24}{5} \mathrm{~cm}\)

BC = 2 x \(\frac{24}{5}\) cm = \(\frac{48}{5}\) cm = 9.6cm

∴ Length of chord BC is 9.6 cm.

Example 3. The length of two chords AB and CD of a circle with its centre O are equal. If ∠AOB 60° and CD = 6 cm; then calculate the length of the radius of the circle.

Solution:

Chord AB = chord DC [given]

In ΔAOB, OA = OB [Radii of same circle]

∴ ∠OBA = ∠OAB = \(\frac{180^{\circ}-\angle \mathrm{AOB}}{2}=\frac{180^{\circ}-60^{\circ}}{2}\) = 60°

∴ ∠OAB = ∠OBA = ∠AOB

∴ OB = OA = AB

∴ ΔAOB is equilateral triangle

∴ OA = AB = CD = 6 cm

∴ The length of radius of the circle is 6 cm.

Class 10 Geometry Chapter 1 Solved Examples

Example 4. P is any point in a circle with its centre O. If the length of the radius is 5 cm and OP = 3 cm. then determine the least length of the chord passing through the point.

Solution:

⇒  The minimum distance of chord AB from centre O of the circle is (OP) = 3 cm.

⇒ length radius (OB) = 5 cm

⇒ In ΔBOP, OP² + BP² = OR² [from Pythagorus theorem]

⇒ 3² + BP² = 5²

⇒ BP = \(\sqrt{25-9}\) cm = 4 cm as OP ⊥ AB

∴ BP = \(\frac{1}{2}\)AB

⇒ AB = 2BP = 2 x 4 cm = 8 cm

∴ Length of chord is 8 cm.

Example 5. The two circles with their centres at P and Q intersect each other, at the points A and B. Through the point A, a straight line parallel to PQ intersects the two circles at the points C and D respectively. If PQ = 5 cm, then determine the length of CD.

Solution:

⇒  From the points P and Q, two perpendiculars PR and QS are drawn on the chord AC and AD respectively which intersects.

⇒ AC at the point R and AD at the point S.

⇒ As PR ⊥ AC and QS ⊥ CD

∴ PR || QS

⇒ Again PQ || RS

∴ PQRS is a parallelogram.

∴ RS = PQ = 5 cm

⇒ PR ⊥ AC,  ∴ AR = \(\frac{1}{2}\) AC

⇒ QS ⊥ AD, ∴ AS =\(\frac{1}{2}\) AD

⇒ AR + AS = \(\frac{1}{2}\) (AC + AD) i.e. RS = \(\frac{1}{2}\) CD

⇒ CD = 2 RS = 2 x 5 cm = 10 cm

Example 6. O is the centre of the circle, if ∠OAB = 30°,∠ABC = 120°, ∠BCO = y° and ∠COA = x°, find x and y.

Solution:

∠AOC is the reflex angle at the centre and ∠ABC is the angle at the circle are formed with the circular arc

∴ Reflex ∠AOC = 2∠ABC = 2 x 120° = 240°

⇒ ∠AOC = 360° – 240°

⇒ x° = 120°

⇒ ∠BCO = 360° – ∠OAB -∠ABC – ∠AOC

⇒ y° = 360° – 30° – 120° – 120°

⇒ y° = 90°

∴ value of x and y are 120 and 90 respectively.

Geometry Theorems Class 10 Solutions

Example 7. O is the circumcentre of the triangle ∠ABC and D is the midpoint of the side BC. If ∠BAC = 40°, find the value of ∠BOD.

Solution:

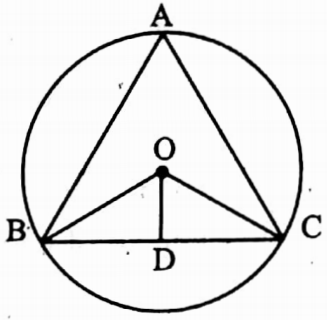
∠BOC is the angle to the centre O and ∠BAC is the angle on the circle formed by circular arc BC

∴ ∠BOC = 2 ∠BAC = 2 x 40° = 80°

⇒ In ΔBOD and ΔCOD

⇒ OB = OC [radii of same circle]

⇒ BD = CD [D is the mid point of BC]

⇒ and OD = OD [common side]

∴ ΔBOD ≅ ΔCOD [By SSS aniom of congruency]

∴ ∠BOD = ∠COD = \(\frac{1}{2}\) ∠BOC = \(\frac{1}{2}\) x 80° = 40°

Example 8. Three points A, B and C lie on the circle with centre O in such a way that ΔOCB is a parallelogram, calculate the value of ∠AOC.

Solution:

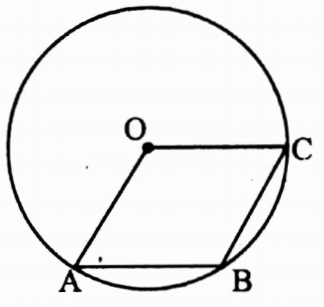
Reflex ∠AOC = 2 ∠ABC

= 2 ∠AOC [opposite angles of OABC parallelogram]

Again, Reflex ∠AOC + ∠AOC = 360°

⇒ 2 ∠AOC + ∠AOC = 360°

⇒ ∠AOC = 360°

⇒ ∠AOC = 120°

Example 9. O is the circumcentre of isosceles triangle ∠ABC and ∠ABC = 120°, if the length of the radius of the circle is 5 cm, find the value of the side AB.

Solution:

I join O, A and O, B

⇒ In ΔAOB and ΔBOC

⇒ AB = BC [given]

⇒ OA = OC [radii of same circle]

⇒ OB = OB [common side]

∴ ΔAOB ≅ ∠BOC [by SSS axiom of congruency]

∴ ∠ABO = ∠CBO = \(\frac{120^{\circ}}{2}\) = 60°

In ΔAOB, OA = OB [same radius]

∴ ∠OAB = ∠ABO = 60°

∠AOB = 180° – 60° – 60° = 60°

∴ ∠AOB = ∠OAB = ∠OBA

⇒  AB = OB = OA = 5 cm

Class 10 Maths Geometry Important Questions

Example 10. Two circles with centres A and B intersect each other at the points C and D. The centre B on the other circle lies on the circle with centre A. If ∠CQD = 70°, find the value of ∠CPD

Solution:

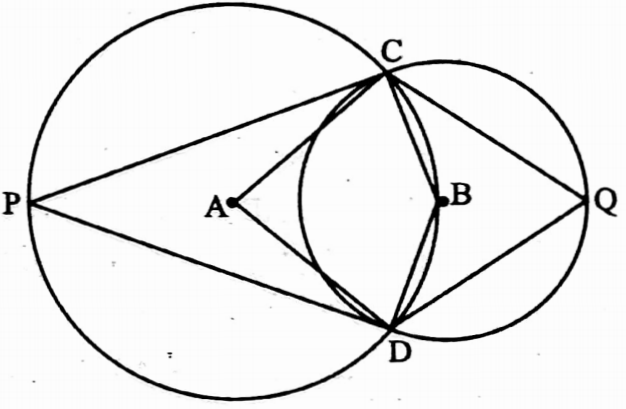
I join A, C; A, D; C, Q and D, Q

⇒ ∠CBD is the angle at centre B and ∠CQD is the angle on the circle at Q formed by a circular arc CD

∴ ∠CBD = 2 ∠CQD

= 2 x 70° = 140°

⇒ Reflex ∠CAD is the angle at the centre A and ∠CBD is the angle on the circle at B formed by circular arc CPD

⇒ Reflex ∠CAD = 2 ∠CBD = 2 x 140° = 280°

∴ ∠CAD = 360° – Reflex ∠CAD = 360° – 280° = 80°

⇒ ∠CAD = 2 ∠CPD

⇒ 80° = 2 ∠CPD

⇒ ∠CPD = 40°

Example 11. O is the centre of the circle, AC is diameter and chord DE is parallel to the diameter AC. IF ∠CBD = 60°, find the value of ∠CDE.

Solution:

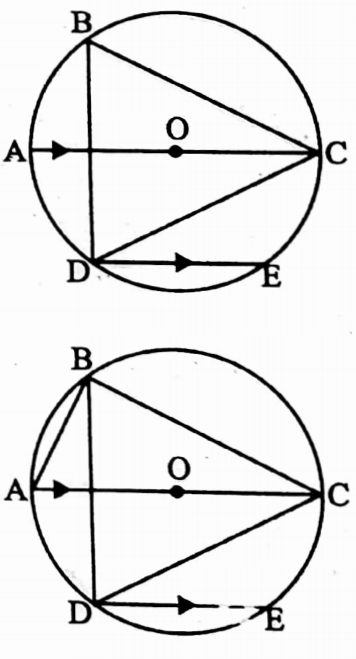
I join A, B

⇒ ∠ABC = 90° [semi-circular angle]

⇒ ∠CBD = 60°

⇒ ∠ABD = 90° – 60° = 30°

⇒ ∠ACD = ∠ABD [angles in the same segment]

= 30°

⇒ AC || DE and CD is the intersection

∴ ∠CDE = alternate ∠ACD = 30°

Class 10 Maths Board Exam Solutions

Example 12. QS is bisector of an angle ∠PQR, if ∠SQR = 35° and ∠PRQ = 32°, find the value of ∠QSR.

Solution:

∠PQR = 2 ∠SQR [QS is the bisector of ∠PQR]

= 2 x 35° = 70°

In ΔPQR, ∠PQR = 70°, ∠PRQ = 32°

∴ ∠QPR = 180° – (70° + 32°) = 78°

∠QSR = ∠QPR [angles in the same segment]

= 78°

Example 13. O is the centre of the circle and AB is diameter. If AB and CD are mutually perpendicular to each other and ∠ADC = 50°, find the value of ∠CAD.

Solution:

I join B, D.

AB and CD intersect at point P.

AB ⊥ CD, ∴ ∠APC = 90°

∠ADB = 90°  [semi-circular angle]

∠ADC = 50°

∠BDC = ∠ADB – ∠ADC = 90° – 50° = 40°

∠BAC = ∠BDC = 40° [angles in the same segment]

In ΔABC, ∠ACB = 90°, ∠BAC = 40°

∴ ∠ABC = 180° – (90° + 40°) = 50°

In ΔPBC, ∠PCB = 180° – (90° + 50°) = 40°

i.e. ∠DCB = 40°

∴ ∠BAD = ∠DCB = 40° [angles in the same segment]

∠CAD = ∠BAC + ∠BAD

= 40° + 40° 80°

Class 10 Maths Board Exam Solutions

Example 14. O is the centre of the circle and AB = AC; if ∠ABC = 32°, find the value of ∠BDC.

Solution:

In ΔABC, AB = AC

∴ ∠ACB = ∠ABC = 32°

∠ADC = ∠ABC [angles in the same segment]

= 32°

Similarly, ∠ADB = ∠ACB = 32°

∴ ∠BDC = ∠ADC + ∠ADB

= 32° + 32° = 64°

Example 15. BX and CY are the bisectors of the angles ∠ABC and ∠ACB respectively. If AB = AC and BY = 4 cm, find the length of AX.

Solution:

In AABC, AB = AC

∴ ∠ACB = ∠ABC

or, \(\frac{1}{2}\) ∠ACB = \(\frac{1}{2}\) ∠ABC

∴ ∠BCY = ∠ABX [BX and CY are bisectors of angle ∠ABC and ∠ACB respectively]

∴ BY = AX

Again, BY = 4 cm

∴ AX = 4 cm.

Example 16. In Isosceles triangle ABC, AB = AC; a circle drawn taking AB as diameter meets the side BC at the point D. If BD = 4 cm find the value of CD

Solution:

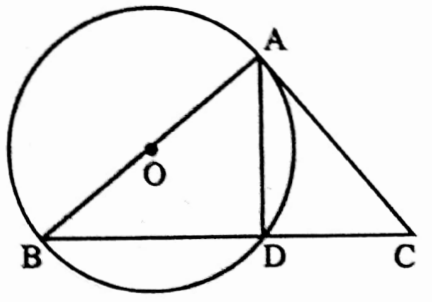
I join A, D

∠ADB = 90° [semicircular angle)

∴ ∠ADC = 180° – 90° = 90°

In ΔABD and ΔACD,

AB = AC, ∠ADB = ∠ADC = 90° and ∠ABD = ∠ACD [AB = AC]

∴ ΔABD ≅ ΔACD [by AAS axiom of congruency]

∴ BD = CD BD = 4 cm

∴ CD = 4 cm

Class 10 Maths Board Exam Solutions

Example 17. Two chords AB and AC of a circle are mutually perpendicular to each other. If AB = 4cm, AC = 3 cm, find the length of the radius of the circle.

Solution:

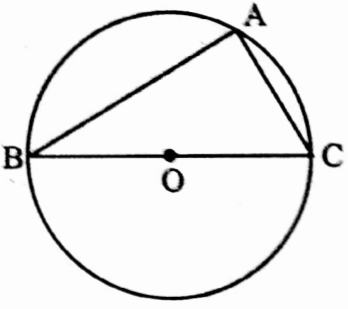
∠BAC = 90° [AB ⊥ AC]

In ΔABC, BC² = AB² + AC² [From Pythagorus theorem]

= (4² + 3²) cm²

= 25 cm²

BC = √25 cm = 5 cm and ∠BAC = 90°.

So BC is diameter of the circle.

∴ length of radius \(\frac{5}{2}\) cm = 2.5 cm

Example 18. Two chords PQ and PR of a circle are mutually perpendicular to each other. If the length of the radius of the circle is r cm, find the length of the chord QR.

Solution:

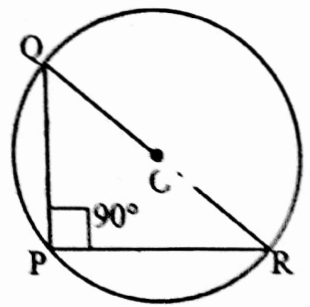
∠QPR = 90° [PQ ⊥ PR]

∴ QR is the diameter of the circle of centre O.

OQ = OR = r cm [given]

∴ QR = 2r cm

Example 19. AOB is a diameter of a circle. The point C lies on the circle. If ∠OBC = 60°, find the value of ∠OCA.

Solution:

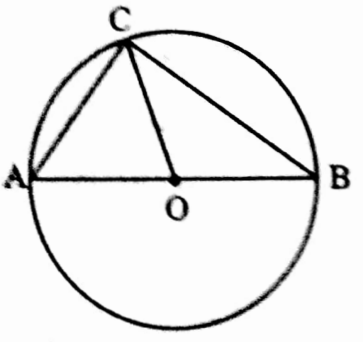
In ΔBOC,

OB = OC [radii of same circle]

∴ ∠OCB = ∠OBC = 60°

∠ACB = 90° [semicircular angle]

∠OCA = ∠ACB – ∠OCB

= 90° – 60° = 30°

WBBSE class 10 Maths Geometry Solutions

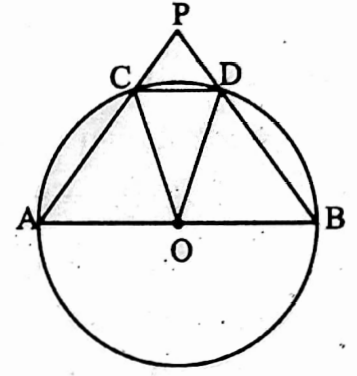
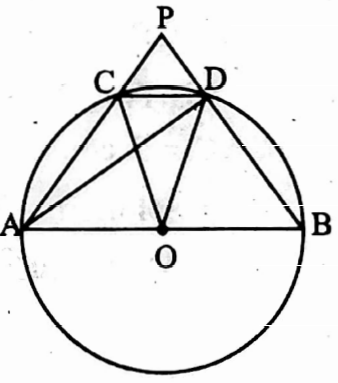
Example 20. In the picture beside, O is the centre of the circle and AB is the P diameter. The length of chord CD is equal to the length of the radius of the circle. AC and BD produced meet at point P, and find the value of ∠APB.

 

Solution:

I join A, D

In ΔCOD, OC = OD [radii of same circle]

∴ CD = OC = OD [according to condition]

∴ ΔCOD is an equilateral triangle

∴ ∠COD = 60°

∠COD is the angle to the centre O and ∠CAD is the angle on the circle at A formed by circular arc DC

∴ ∠CAD = \(\frac{1}{2}\) ∠COD = \(\frac{1}{2}\) x 60° = 30°

i.e. ∠PAD = 30°

again ∠ADB = 90° [semi-circular angle]

∴ ∠ADP = 180° – 90° = 90°

In ΔAPD, ∠APD = 180° – ∠ADP – ∠PAD

= 180° – 90° – 30° = 60°

i.e. ∠APB = 60°

Example 21. In the picture beside two circles with centres P and Q intersecting each at points B and C. ACP is a line segment. If ∠ARB = 150°, ∠BQD = x°, find the value of x.

 

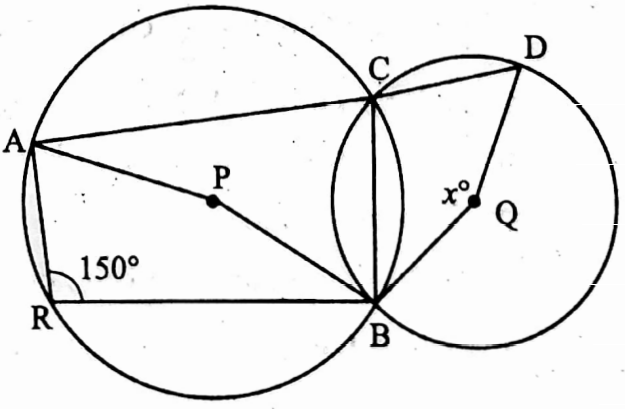
Solution: Reflex ∠APB is the angle to the centre P and ∠ARB is angle on the circle formed by circular arc ACB

∴ Reflex ∠APB = 2 ∠ARB = 2 x 150° = 300°

∴ ∠APB = 360° – Reflex ∠APB

= 360° – 300° = 60°

Angle ∠APB is the angle to the centre P and ∠ACB is the angle on the circle formed by circular arc ARB

∴ ∠ACB = \(\frac{1}{2}\) ∠APB = \(\frac{1}{2}\) x 60° = 30°

∴ ∠BCD = 180° – ∠ACB = 180° – 30° = 150°

Similarly reflex ∠BQD = 2 ∠BCD = 2 x 150°

∴ ∠BQD = 360° – reflex ∠BQD

x° = 360° – 300° = 60°

∴ the value of x is 60.

WBBSE class 10 Maths Geometry Solutions

Example 22. In picture beside two circles intersect at the points P and Q. If ∠QAD = 80° and ∠PDA = 84°, find the value of ∠QBC and ∠BCP.

 

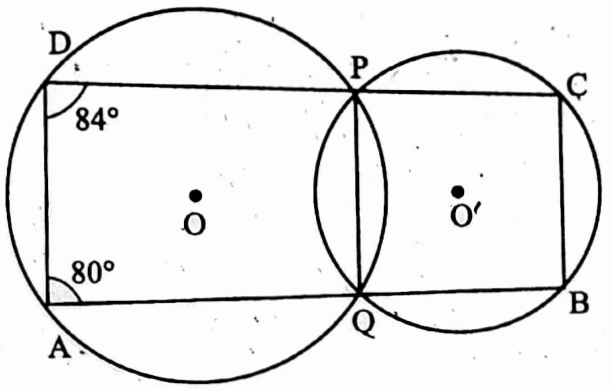
Solution: ln ADPQ cyclic quadrilateral,

exterior ∠QPC = interior opposite ∠QAD = 80° and exterior ∠PQB = interior opposite ∠PDA = 84°

PQBC is a cyclic quadrilateral

∴ ∠QBC + ∠QPC = 180°

∠QBC + 80° =180°

or, ∠QBC = 100°

Again, ∠BCP + ∠PQB = 180°

∠BCP + 84° = 180°

or, ∠BCP = 96°

Example 23. In picture beside, if ∠BAD = 60°, ∠ABC = 80°, then find the value of ∠DPC and ∠BQC.

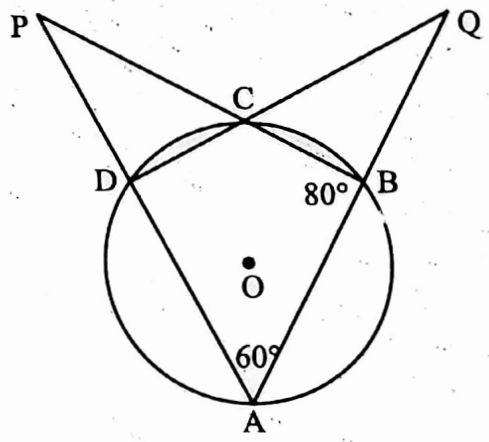
Solution: In ΔABP, ∠BAP = 60° and ∠ABP = 80°

∴ ∠APB = 180° – 60° – 80° i.e. ∠DPC = 40°

In ABCD cyclic quadrilateral, ∠ADC + ∠ABC = 180°

∠ADC + 80° = 180°

⇒ ∠ADC = 180° – 80° = 100°

In ΔADQ, ∠QAD = 60°, ∠ADQ = 100°

∴ ∠AQD = 180° – 60° – 100° = 20°

i.e., ∠BQC = 20°

Example 24. In picture beside O is the centre of circle and AC is diameter. If ∠AOB = 80° and ∠ACE = 10°, find the value of ∠BED.

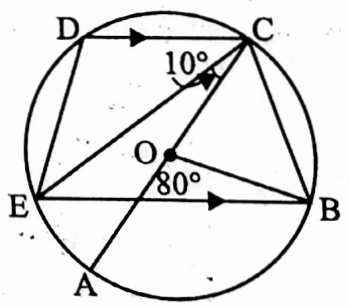
Solution: ∠BOC = 180° – ∠AOB = 180° – 80° = 100°

∠BOC is the angle to centre O and ∠BEC is the angle on the circle at E formed by circular arc BC

∴ ∠BEC = \(\frac{1}{2}\) ∠BOC = \(\frac{1}{2}\) x 100° = 50°

DC || EB and EC its intersection

∴ ∠DCE = alternate ∠BEC = 50°

Similarly, ∠ACB = \(\frac{1}{2}\) ∠AOB = \(\frac{1}{2}\) x 80° = 40°

∠BCD = ∠ACB + ∠ACE + ∠DCE = 40° + 10° + 50° = 100°

In BCDE cyclic quadrilateral, ∠BED + ∠BCD = 180°

∠BED + 100° = 180°

⇒ ∠BED = 80°

WBBSE class 10 Maths Geometry Solutions

Example 25. In picture beside O is the centre of circle and AB is diameter. If ∠AOD = 140° and ∠CAB = 50°, find the value of ∠BED.

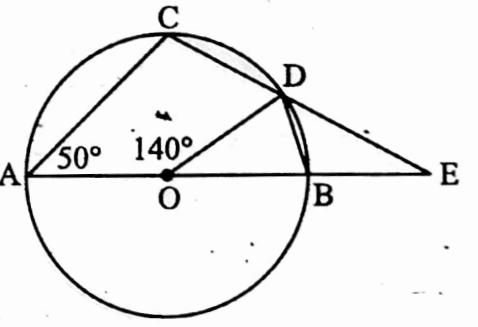
Solution: ∠AOD is the angle to centre O and ∠ABD is the angle on the circle at B formed by circular arc ACD.

∴ ∠ABD = \(\frac{1}{2}\) ∠AOD = \(\frac{1}{2}\) x 140° = 70°

∴ ∠DBE = 180° – 70° = 110

In cyclic quadrilateral ABCD, exterior ∠BDE = interior opposite ∠CAB = 50°

In ΔDBE, ∠BED = 180° – ∠BDE – ∠DBE

= 180° – 50° – 110° = 20°

Example 26. The perpendicular distance of a chord from the centre of a circle, having the radius of 5 cm is 3 cm in length. Calculate the length of its chord.

Solution:

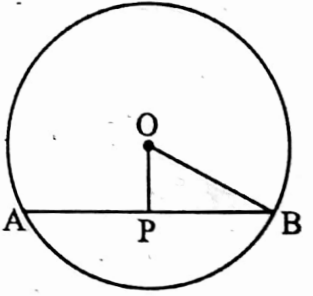
Let, the length of the radius of the circle with its centre O and the perpendicular distance of the chord AB from O is OP where OP = 3 cm

In ΔBOP, ∠OPB = 90° [OP ⊥ AB]

OP² + BP² = OB² [From Pythagorus theorem]

3² + BP² = 5²

⇒ BP = \(\sqrt{25-9}\) cm = √16 cm = 4 cm

∴ As, OP ⊥ AB

∴ BP = \(\frac{1}{2}\) AB [the perpendicular drawn on the chord, which is not a diameter, from the centre of the circle, bisects the chord]

⇒ AB = 2 BP

= 2 x 4 cm = 8 cm

∴ Length of chord is 8 cm.

WBBSE class 10 Maths Geometry Solutions

Example 27. The length of chord PQ of a circle with its centre O is 32 cm. If the length of radius of circle is 20 cm. then find the perpendicular distance from the centre O to the chord PQ.

Solution:

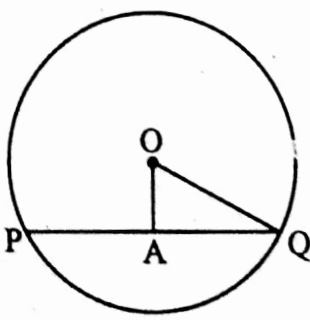
The perpendicular OA, drawn on the chord PQ from centre O, intersects PQ at the point A.

∴ AQ = \(\frac{1}{2}\) PQ

= \(\frac{1}{2}\) x 32 cm = 16 cm

In right angle triangle AOQ,

OA² + AQ² = OQ² [By Pythagorus theorem]

OA² = OQ² – AQ²

= (20² – 16²) cm²

OA = \(\sqrt{400-256}\) cm

= √144 cm = 12 cm

∴ The distance from 0 to chord PQ is 12 cm.

Example 28. The perpendicular distance from the centre of a circle to a chord of length 1 2 cm is 4.5 cm. Find the length of diameter of the circle.

Solution:

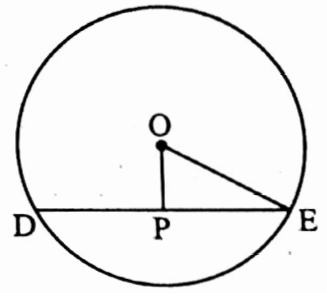
Let the perpendicular distance from the centre O of a circle to a chord DE is OP,

DE = 12 cm, OP = 4.5 cm

I join O, E,

Hence OE is the radius of the circle as OP ⊥ DE

∴ PE = \(\frac{1}{2}\) DE

= \(\frac{1}{2}\) x 12 cm = 6 cm

In ΔPOE, ∠OPE – 90°

∴ OE² = OP² + PE² = { (4.5)² + (6)²} cm²

= (20.25 + 36) cm² = 56.25 cm²

OE = \(\sqrt{56 \cdot 25}\) cm = 7.5 cm

∴ Diameter of the circle is (2 x 7.5) cm or 15 cm.

Class 10 Maths Geometry Chapter 1 Solutions

Example 29. Two chords AH and CD of length x cm and y cm respectively produce an angles 60° and 90° to the centre O of a circle. Establish the relation between x and y. [x> 0, y>0]

Solution:

AB = x cm, CD = y cm ∠AOB = 60° and ∠COD = 90°

In ΔAOB, OA = OB [radii of same circle]

∴ ∠OBA = ∠OAB = \(\frac{180^{\circ}-\angle \mathrm{AOB}}{2}=\frac{180^{\circ}-60^{\circ}}{2}\) = 60°

∴ ΔAOB is equilateral triangle.

∴ OA = OB = AB = x cm.

In ΔCOD, OC = OD = x cm

∠COD = 90°

OC² + OD² = CD²

x² + x² = y²

⇒ 2x² = y²

⇒ √2x = y

∴ This is the relation between x and y.

Example 30. The lengths of two parallel chords of a circle with a radius 5 cm in length 8 cm and 6 cm. Calculate the distance between two chords if they are in same side of the centre.

Solution:

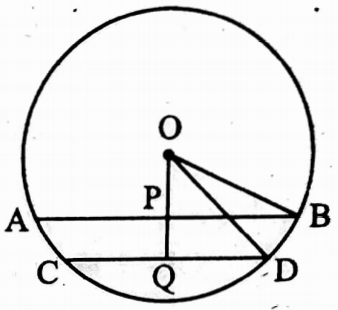
Let, the length of the radius of the circle with its centre O be 5 cm. and the two chords AB and CD are in the same side the centre.

The lengths of AB and CD are 8 cm. and 6 cm. respectively. AB || CD.

From the point O, a perpendicular OQ is drawn on the chord CD which intersects AB at the point P.

Since AB || CD and OQ ⊥ CD, ∴ OP ⊥ AB.

∠OQD = corresponding ∠OPB = 90°

∴ BP = \(\frac{1}{2}\) AB = \(\frac{1}{2}\) x 8 cm = 4 cm

Again, OB = 5 cm

In right angled ΔBOP, OP² + BP² = OB²

⇒ OP² = BP² – BP² = (5² – 4²) cm² = 9 cm²

OP = √9 cm = 3 cm

In ΔQOD, ∠OQD = 90°

∴ OQ² + QD² = OD².

OQ² = OD² – QD² = (5² – 3²) cm2 = 16 cm²

OQ = √16 cm = 4 cm

∴ The distance between the cords AB and CD is PQ = OQ – OP = (4 – 3) cm = 1 cm

Example 31. O is the centre of the circle. ∠POT = 50° and ∠PRQ = 40°, Find the values of ∠QRT and ∠QOT.

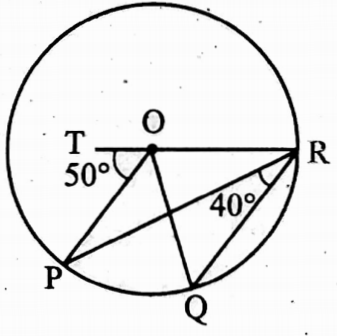
Solution: ∠POQ is the angle to centre O and ∠PRQ is the angle on the circle at R formed by circular arc PQ

∴ ∠POQ = 2 ∠PRQ

∴ ∠POQ = 2 x 40° = 80°

∠QOT = ∠POQ + ∠POT

∠QOT = 80° + 50° = 130°

Example 32. O is the centre of the circle. If ∠AOC + ∠BOD = 100°, then find the value of ∠APC.

Solution:

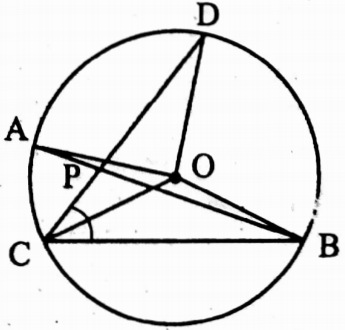
I join B, C

∠AOC + ∠BOD

= 2 ∠ABC + 2 ∠BCD [The angle at the centre is double the angle on the circle, subtended by same arc]

= 2 ∠APC

2 ∠APC = 100°

⇒ ∠APC = 50°

Basic Geometrical Concepts Class 10 Solutions

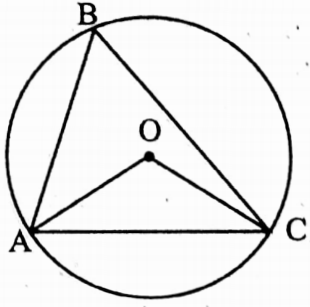
Example 33. The circumcentre of ΔABC is O; if ∠OBC = 50°, then find the value of ∠BAC.

Solution:

In Δ BOC, OB = OC [radii of same circle]

∠OCB = ∠OBC = 50°

∠BOC = 180° – (50° + 50°) = 80°

∠BAC = \(\frac{1}{2}\) ZBOC = \(\frac{1}{2}\) x 80° = 40°

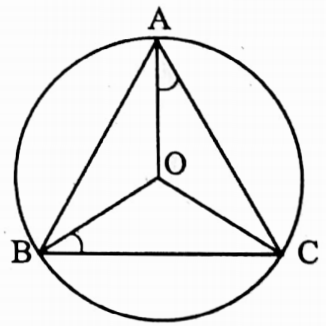
Example 34. The circumcentre of ΔABC is O; if ∠BAC = 85° and ∠BCA = 55° find the value of ∠OAC.

Solution:

In ΔABC,

∠BAC = 85°, ∠BCA = 55°

∴ ∠ABC = 180° – (85° + 55°) = 40°

∠AOC = 2 ∠ABC = 2 x 40° = 80°

In ΔAOC, OA = OC [radii of the same circle]

∠OCA = ∠OAC = \(\frac{180^{\circ}-\angle \mathrm{AOC}}{2}=\frac{180^{\circ}-80^{\circ}}{2}\) = 50°

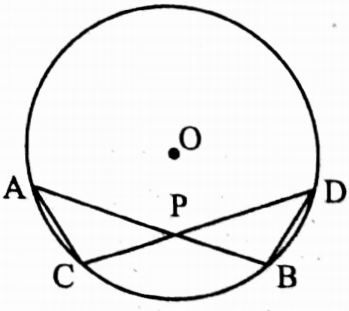
Example 35. O is centre of the circle, ∠OAC = x°, ∠OBC = y°; find the value of ∠OAB.

Solution: In ΔAOC, OA = OC [radii of same circle]

∴ ∠OCA = ∠OAC = x°

In ΔBOC, OB = OC

∠OCB = ∠OBC = y°

∠ACB = ∠OCA + ∠OCB = x° + y°

∠AOB = 2 ∠ACB = 2 (x° + y°)

In ΔAOB, OA = OB

∴ ∠OBA = ∠OAB = \(\frac{180^{\circ}-\angle \mathrm{AOB}}{2^{\circ}}\)

= \(\frac{180^{\circ}-2\left(x^{\circ}+y^{\circ}\right)}{2}\)

∴ ∠OBA = 90°-x°-y°

Example 36. O is the centre of the circle, if ∠BPC = 100° and ∠PBD = 70° then find the value of ∠BAC.

Solution: In ΔPBD,

exterior ∠BPC = ∠PDB + ∠PBD

∴ 100° = ∠PDB + 70°

⇒ ∠PDB = 30° i.e. ∠CDB = 30°

Again ∠BAC =∠CDB [angles in the same segment]

∠BAC  = 30°

Example 37. AB is the diameter of the circle with its centre O; if ∠ABC = 40°, find the value of ∠BDC.

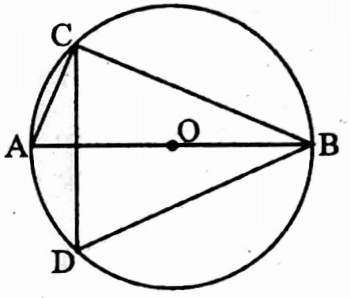
Solution: ∠ACB = 90° [Semi circular angle]

In ∠ABC, ∠BAC = 180° – ∠ACB = ∠ABC

= 180° – 90° – 40° = 50°

∠BDC = ∠BAC [angles in the same segment]

∠BDC  = 50°

Example 38. O is the centre of the circle, if ∠AOB = 110° and ∠DCA = 40° then find the value of ∠BAD and ∠ADB.

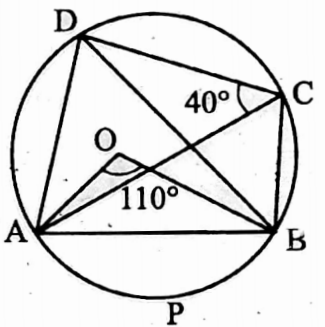
Solution: 2 ∠ACB = ∠AOB [the angle at the centre is double the angle =110° on the circle, subtended by same arc]

∠ACB = 55°

∠BCD = ∠DCA + ∠ACB

= 40° + 55° = 95°

In ABCD cyclic quadrilateral,

∠BAD + ∠BCD = 180°

∠BAD + 95° = 180°

⇒ ∠BAD = 85°

∠ADB = ∠ACB [angles in the same segment] = 55°

Class 10 Geometry Chapter 1 Solved Examples

Example 39. If ABCD is a cyclic parallelogram find the value of ∠BAC.

Solution:

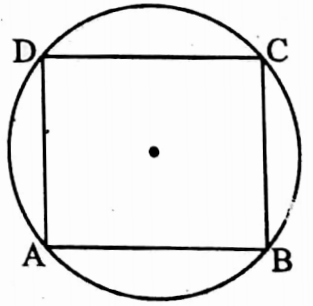
In cyclic parallelogram ABCD,

∠A + ∠C =180°

again ∠A = ∠C [as ABCD is a parallelogram]

∠A + ∠A = 180°

2 ∠A = 180°

⇒ ∠A = 90° [cyclic parallelogram is a rectangular picture]

Example 40. If an angle of the cyclic trapezium is 40° then find the values of other angles.

Solution:

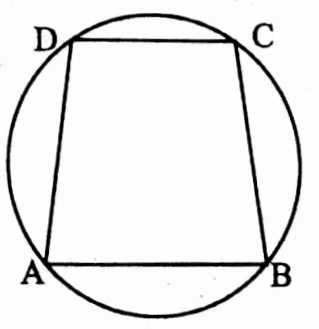
Let AB || DC of a cyclic trapezium and ∠BAD = 40°as AB || DC and AD is the intersection

∴ ∠BAD + ∠ADC = 180°

40° + ∠ADC = 180°

⇒ ∠ADC = 140°

again ABCD is also a cyclic quadrilateral

∴ ∠BCD + ∠BAD = 180°

∠BCD + 40° =180°

∠BCD = 140°

∠ABC = 180° – ∠ADC

= 180° – 140° = 40°

values of other angles are 40°, 140°, 140° [cyclic trapezium is isosceles trapezium]

Example 41. Side AB of a cyclic quadrilateral ABCD is produced to the points X, if ∠XBC = 82° and ∠ADB = 47° then the find the value of ∠BAC.

Solution:

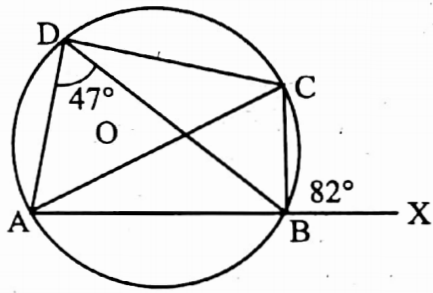
In cyclic quadrilateral ABCD, exterior ∠XBC = interior opposite ∠ADC

= 82° = ∠ADC

∠BDC = ∠ADC – ∠ADB

= 82° – 47° = 35°

∠BAC = ∠BDC [angles in the same segment]

= 35°

The value of ∠BAC = 35°

Example 42. If the ratio of three consecutive angles of a cyclic quadrilateral is 1: 2 : 3 then determine the 1st and 3rd angles.

Solution: Let the measurement of these consecutive angles is x°, 2x° and 3x°

[x is common multiple and x > 0]

The opposite angles a cyclic quadrilateral are supplementary.

∴ x° + 3x° = 180°

⇒ 4x° = 180°

⇒ x° = 45°

The measurement of 1st angle is 45° and third angle is 45° x 3 or 135°

Example 43. AB is a diameter and ∠ACB is a semicircular angle of a circle of radius 4 cm in length. If BC = 2√7 cm, find the length of AC.

Solution:

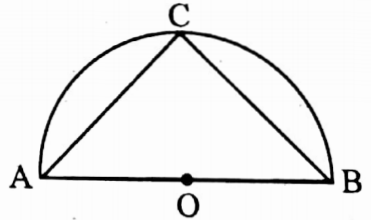
∠ACB = 90°

In ΔACB, AC² + BC² = AB²

⇒ AC² = AB² – BC² = {(2 x 4)² – (2√7 )²} cm²

⇒ AC = \(\sqrt{64-28}\) cm = √36 cm = 6 cm.