WBBSE Solutions For Class 10 Maths Geometry Chapter 2 Theorems Related To Tangent Of A Circle

Geometry Chapter 2 Theorems Related To Tangent Of A Circle

There are three different situations between a circle and a line in a plane.

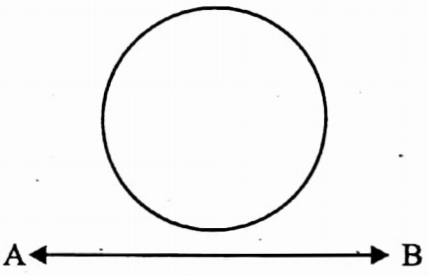
⇔ The straight line AB does not intersect the circle.

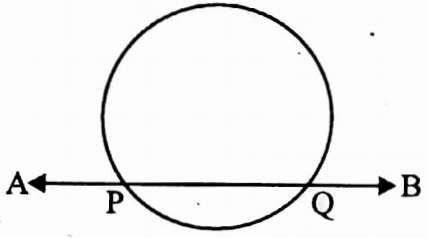
⇔ The straight line AB intersects the circle at two points P and Q.

Read and Learn More WBBSE Solutions for Class 10 Maths

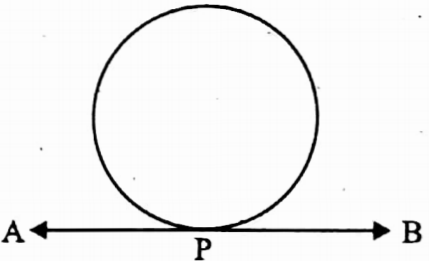
⇔ The straight line AB intersects the circle at point P.

⇔ Secant: A straight line which intersects a circle in two distinct points is called a secant of circle.

⇒ AB is a secant of a circle with centre O.

Class 10 Maths Geometry Chapter 2 Solutions

⇔ Tangent: When a straight line intersects the circle in only one point, the straight line is said to be a tangent to the circle and point is called the point contact of the tangent.

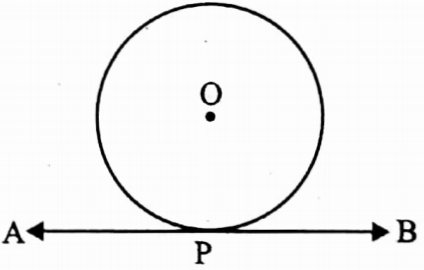
⇒ AB is a tangent and P is the point of contact.

⇔ Common tangent: If a straight line touches each of two circles, then the straight line is called a common tangent of two circles.

⇔ Common tangents are two types:

1. Direct common tangent,
2. Transverse common tangent.

⇔ Direct common tangent: If the position of two circles are the same side of a common tangent.

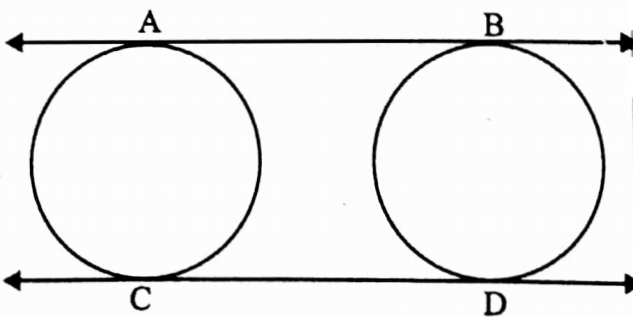
⇒ Then the tangent is called a direct common tangent. AB and CD are direct common tangents.

⇔ Transverse common tangent: If the position of two circles are the opposite side of a common tangent then the tangent is called a transverse common tangent.

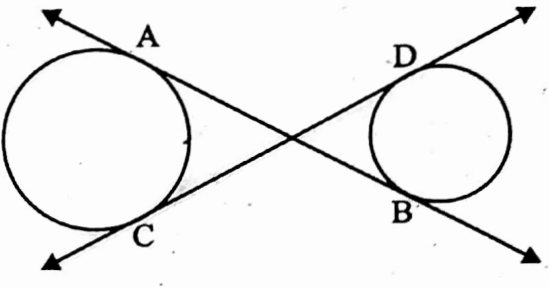
⇒ AB and CD are transverse common tangents.

Theorems:

1. The tangent and the radius passing through the point of contact are perpendicular to each other.
2. If two tangents are drawn from an external point, the line segments joining the point of contact and the exterior point are equal and they subtend equal angles at the centre.
3. If two circles touch each other, then the point of contact will lie on the line segment joining the two centres.

Geometry Chapter 2 Theorems Related To Tangent Of A Circle True Or False

Example 1. P is a point inside a circle. Any tangent drawn on the circle does not pass through the point P.

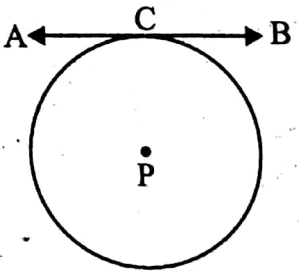
Solution: Clearly the statement is true.

Circles Class 10 Solutions

Example 2. There are more than two tangents can be drawn to a circle parallel to a fixed line.

Solution: Clearly the statement is false.

Geometry Chapter 2 Theorems Related To Tangent Of A Circle Fill In The Blanks

Example 1. If a straight line intersects the circles at two points, then the straight line is called _______ of circle.

Solution: Intersection.

Example 2. If two circles do not intersect or touch each other, then the maximum number of common tangents can be drawn is _________

Solution: Four

Example 3. Two circles touch each other externally at the point A. A common tangent drawn to two circles at the point A is _______ common tangent.

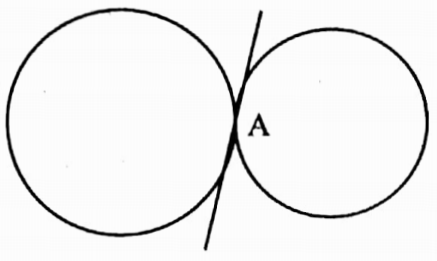
Solution: Transverse

Geometry Chapter 2 Theorems Theorems Related To Tangent Of A Circle Short Answer Type Question

Example 1. O is the centre and BOA is a P diameter of the circle. A tangent drawn to a circle at the point P intersects the extended BA at the point T. If ∠PBO = 30°, find the value of ∠PTA.

Solution: In ΔPOB, OP = OB [radii of same circle]

∴ ∠OPB = ∠PBO

⇒ Again exterior ∠POT = ∠PBO + ∠OPB

= 30° + 30° = 60°

As TP is tangent and P is a radius of the circle with centre O

‎∴ OP ⊥ PT ; ∠OPT = 90°

In ΔPOT, ∠PTA = 180° – (∠OPT + ∠POT)

∠PTA = 180° – (90° + 60°) = 30°

Class 10 Geometry Chapter 2 Solved Examples 

Example 2. ΔABC circumscribed a circle and touches the circle at the points P, Q, R. If AP = 4 cm, BP = 6 cm, AC = 12 cm and BC = x cm, then determine the value of x.

Solution: I join, O, A; O, B; O, C; O, P; O, Q and O, R

AP and AR are two tangents to a circle with centre O, drawn from the exterior point A,

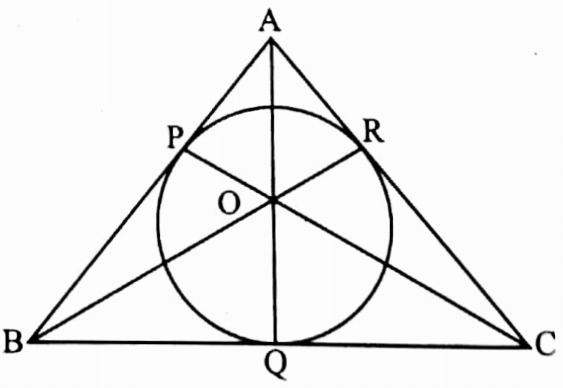
So, AR = AP = 4 cm

⇒ Similarly, BQ = BP = 6 cm and CQ = CR

= AC – AR = (12 – 4) cm = 8 cm

∴ BC = BQ + CQ = (6 + 8) cm = 14 cm

∴ The value of x is 14.

Example 3. The circles with centres A, B, C touch one another externally. If AB = 5 cm, BC = 7 cm and CA = 6 cm. Find the length of radius of circle with centre A.

Solution: Two circles with centres A and B touch each other externally at P

∴ A, P and B are collinear.

⇒ Similarly, A, Q and C are collinear

⇒ B, R and C are collinear

⇒ Let AP = AQ = x cm [radii of same circle]

⇒ BP = BR = y cm

⇒ and CR = CQ = z cm

⇒ AP + BP = AB

⇒ x + y = 5…….(1)

⇒ BR + CR = BC

⇒ y + z =7……(2)

⇒ CQ + AQ = CA

⇒ z + x = 6………(3)

(1) + (2) + (3)

⇒ 2(x + y + z) = 5 + 7 + 6

⇒ or, x + y + z = 9 ………(4)

(4) – (2)

⇒ x + y + z – y – z = 9 – 7

⇒ x = 2

∴ The length of the radius of a circle with centre O is 2 cm.

Example 4. Two tangents drawn from enternal point C to a circle with centre Q touches the circle at the points P and Q respectively. A tangent drawn at another point R of a circle intersects CP and CA at the points A and B respectively. If CP = 11 cm and BC = 7 cm, determine the length of BR.

Solution: CP and CQ are tangents of a circle with centre O.

⇒ So, CQ = CP = 11 cm

⇒ BQ = CQ – BC = (11 – 7) cm = 4 cm

⇒ Again, BR = BQ = 4 cm [as BR and BQ are two tangent of a circle]

Example 5. The lengths of radii of two circles are 8 cm and 3 cm and distance between two centre is 13 cm. Find the length of a common tangent of two circles.

Solution: Let BE is a direct common tangent of two circles with centres A and B respectively.

I join A, D and B, E

The distance between two circle is AB where AB = 13 cm

A perpendicular BC is drawn from B to AC, DE is a tangent and AD is a radius of the circle with centre A

∴ AD ⊥ DE similarly BE ⊥ DE

∴ AD || BE i.e. CE || BE

⇒ Again, BC ⊥ AD and DE ⊥ AD  ∴ BC || DE

⇒ In quadrilateral BCDE, CD || BE and BC || DE

∴ BCDE is a parallelogram

∴ DC = BE = 3 cm and DE = BC

⇒ AC = AD – DC = (8 – 3) cm = 5 cm

⇒ In right angled ΔABC, ∠ACB = 90°

∴ AC² + BC² = AB² [from Pythagorus theorem

⇒ BC = \(\sqrt{\mathrm{AB}^2-A C^2}\)

= \(\sqrt{13^2-5^2} \mathrm{~cm}\)

= √144 cm = 12 cm

∴ DE = BC = 12 cm

∴ The length of a common tangent of two circle is 12 cm.

Wbbse Class 10 Geometry Notes

Example 6. The length of radius of a circle with centre O is 6 cm. P is a point at the distance of 10 cm from the centre. Find the length of the tangent PQ from the point P to the circle.

Solution: PQ is a tangent to the circle with centre O and OQ is a radius of the circle.

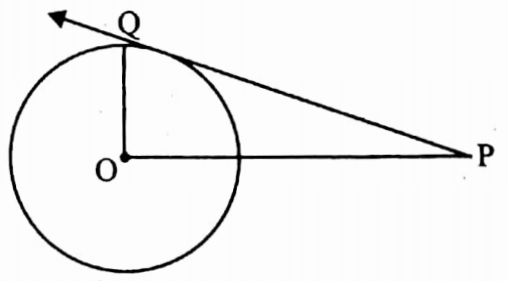
∴ OQ ⊥ PQ

⇒ In right-angled ΔPOQ, ∠OQP = 90°

∴ OQ² + PQ² = OP² [from Pythagorus teorem]

⇒ PQ = \(\sqrt{\mathrm{OP}^2-\mathrm{OQ}^2}\)

= \(\sqrt{(10)^2-(6)^2} \mathrm{~cm}\)

= √64 cm = 8 cm

∴ Length of the tangent is 8 cm.

Example 7. A circle with centre O, a point P is 20 cm away from the centre of the circle and the length of the tangent PQ to the circle is 16 cm. Find the length of the diameter of the circle.

Solution: OQ is a radius and PQ is tangent to the circle with centre O

∴ OQ ⊥ PQ

⇒ In right angled triangle ΔPOQ, ∠OQP = 90°

⇒ OQ² + PQ² = OP² [From Pythagoras theorem]

⇒ OQ = \(\sqrt{\mathrm{OP}^2-\mathrm{PQ}^2}\)

= \(\sqrt{20^2-16^2} \mathrm{~cm}=\sqrt{400-256} \mathrm{~cm}=\sqrt{144} \mathrm{~cm}=12 \mathrm{~cm}\)

⇒ length of radius is 12 cm

⇒ Length of a diameter of the circle is (12 x 2) cm or 24 cm

Example 8. The lengths of radius of two concentric circles arc 3 cm and 5 cm respectively. If a tangent of the smaller circle is a chord of the larger circle, find the length of that chord.

Solution: Let O be the centre of two concentric circles.

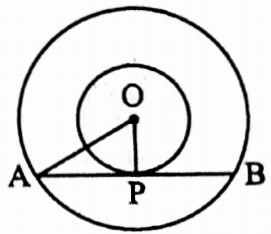
⇒ AB is a tangent of the smaller circle at point P

⇒ So AB is a chord of the larger circle.

⇒ Radius of smaller circle (OP) = 3 cm and radius pf larger circle (OA) = 5 cm

⇒ As AB is a tangent and OP is a radius of the circle

∴ OP ⊥ AB  ∴ ∠APO = 90°

⇒ In right angled ΔAPO, AP² + OP² = OA²

⇒ AP = \(\sqrt{\mathrm{OA}^2-\mathrm{OP}^2}\)

⇒ = \(\sqrt{5^2-3^2} \mathrm{~cm}\) = √16 cm = 4 cm

⇒ In larger circle, AP ⊥ AB

∴ AB = 2AP = (2 x 4) cm = 8 cm

∴ Length of the chord is 8 cm.

Circle Theorems Class 10 Solutions 

Example 9. The length of a chord AB of a circle with centre O is 6 cm at the length of radius of that circle is 5 cm. Two tangents are drawn at the points A and B of the circle intersect at P. Find the length each of the tangent.

Solution: I join O, A; O, B and O, P.

AB and OP are intersect at M.

If two tangents are drawn to a circle from a point outside it, then the line segments joining the points of contact and the exterior are equal and they subtend equal angles at the centre.

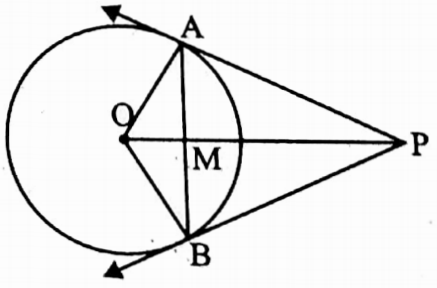
∴ PA = PB and ∠AOP = ∠BOP

⇒ i.e. ∠AOM = ∠BOM

⇒ In ΔAOM and ΔBOM,

⇒ OA = OB [radii of same circle]

⇒ OM = OM [common side]

⇒ and ∠AOM = ∠BOM

∴ ΔAOM ≅ ΔBOM [By SAS axiom of congruency]

∴ AM = BM = \(\frac{1}{2}\) AB

= (\(\frac{1}{2}\) x 6) cm = 3 cm and ∠AMO = ∠BMO = \(\frac{180^{\circ}}{2}\) = 90°

In right angled triangle AOM, OM² + AM² = OA²

⇒ OM = \(\sqrt{\mathrm{OA}^2-\mathrm{AM}^2}\)

= \(\sqrt{5^2-3^2} \mathrm{~cm}\)

∴ Let PM = x cm and PA = PB = y cm  ∴ OP = (4 + x) cm

As PA is a tangent at A and OA is a radius of the circle.

∴ OA ⊥ AP  ∴ ∠OAP = 90°

In right-angled ΔAOP, OA² + PA² = OP²

5² + y² = (4 + x)²

⇒ y² = (4 + x)² – 25…….(1)

In right-angled ΔAMP, AM² + PM² = AP²

3² + x² = y² ……(2)

From (1) and (2), (4 + x)² – 25 = 9 + x²

⇒ 16 + 8x + x² – 25 = 9 + x²

⇒ 8x = 18

⇒ x = \(\frac{9}{4}\)

From (2), y² = 3² + \(\left(\frac{9}{4}\right)^2\) = 9 + \(\frac{81}{16}\) = \(\frac{225}{16}\)

y= \(\sqrt{\frac{225}{16}}=\frac{15}{4}\) = 3.75

∴ Length of each tangent is 3.75 cm.

Example 10. PQ is a chord of a circle with centre O. A tangent Is drawn at the point Q which intersects extended PQ at the point R. If ∠PRQ = 30° then calculate the value of ∠RPQ.

Solution: In joining O, Q

RQ is a tangent at Q and OQ is a radius of that circle

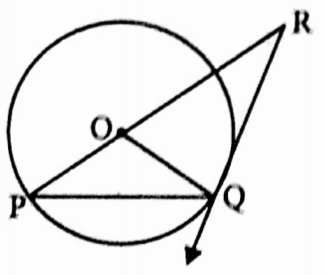
∴ OQ ⊥ RQ  ∴ ∠OQR = 90°

⇒ In ΔPOQ, OP = OQ [radii of same circle]

⇒ ∠OPQ = ∠OQP

⇒ the exterior ∠QOR = ∠OPQ + ∠OQP

⇒ 60° = ∠OPQ + ∠OPQ

⇒ 2 ∠OPQ = 50°

⇒ ∠OPQ = 30°

i.e. ∠RPQ = 30°

Class 10 Maths Geometry Important Questions 

Example 11. AB and CD are two tangents of a circle with centre O at P and Q respectively. Another tangent EF is drawn which intersects AB and CD at E and F respectively. If AB || CD then find the value of ∠EOF.

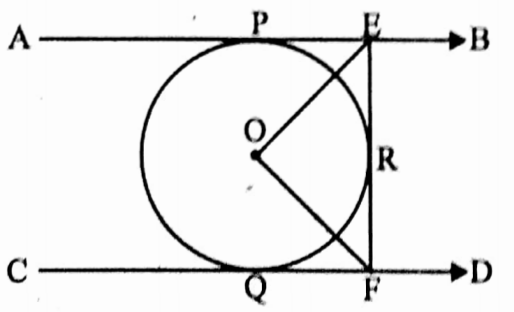
Solution: I join, O, P; O, Q and O, R.

⇒ EP and ER are tangents to a circle with centre O.

∴ PE = RE

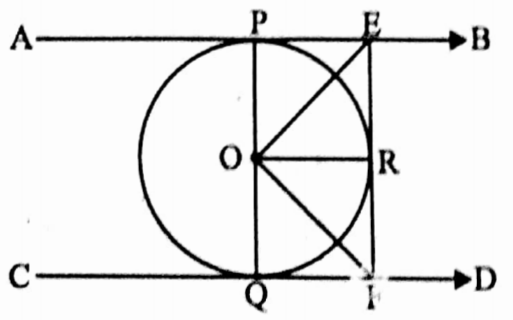
In ΔPOE and ΔROE

⇒ OP = OR [radii of same circle]

⇒ OE = OE [common side]

⇒ PE = RE

∴ ΔPOE = ΔROE [by SSS axiom of congruency]

∴ ∠POE = ∠REO = \(\frac{1}{2}\) ∠PER

Similarly ΔROF = ΔQOF

∴ ∠RFO = ∠QFO = \(\frac{1}{2}\) ∠QFR

AB || CD and EF is intersection

∴ ∠PER + ∠QFR = 180°

∴ 2 ∠REO + 2 ∠RFO = 180°

⇒ ∠REO + ∠RFO = 90°

⇒ In ΔEOF, ∠EOF = 180° – (∠REO + ∠RFO)

= 180° – 90° = 90°

Example 12. Two tangents AB and AC drawn from an external point A of a circle with centre O touch the circle at an point B and C. A tangent drawn to a point D lies on minor arc BC intersects AB and AC at points E and F respectively. If AB = 4 cm then find the perimeter of the ΔAEF.

Solution: As AB and AC are tangents to a circle with centre O,

∴ AB = AC

⇒ Similarly, EB = ED and FD = FC

⇒ Perimeter of ΔAEF, AE + EF + AF

= AE + (ED + FD) + AF = AE + (EB + FC) + AF

= (AE + EB) + (FC + AF) = AB + AC = AB + AB

= 2AB = 2 x 4 cm s 8 cm

Example 13. Three equal circles touch one another externally. The length of radius of each circle is 5cm. Find the perimeter of the triangle obtained by joining the centres.

Solution: Three circles with centre A, B and C touch one another externally at points P, Q and R.

⇒ The points A, P, and B are collinear; B, Q, and C are collinear and C, R, and A are collinear.

⇒ Again, AP = BP = BQ = CQ = CR = AR = 5 cm

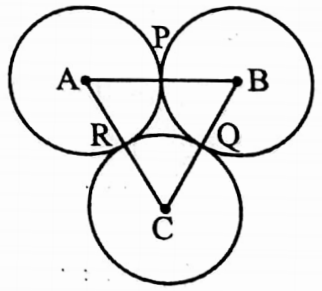
∴ AP + BP = BQ + CQ = CR + AR = (5 + 5) cm

⇒ i.e. AB = BC = CA = 10 cm

∴ Perimeter of the ΔABC is (10 x 3) cm = 30 cm

Class 10 Maths Board Exam Solutions

Example 14. BC is diameter of the circle with centre O and PAQ is a tangent at A. If ∠PAB = 60°, then find the values of ∠CAQ and ∠ABC.

Solution:

⇒ ∠BAC = 90° [semi circular angle]

⇒ ∠PAB + ∠BAC + ∠CAQ = 180°

⇒ 60° + 90° + ∠CAQ = 180°

⇒ ∠CAQ = 30°

∠ABC = alternate circular ∠CAQ = 30°