WBBSE Solutions For Class 10 Maths Trigonometry Chapter 2 Trigonometric Ratios And Trigonometric Identities

Trigonometry Chapter 2 Trigonometric Ratios And Trigonometric Identities

Trigonometric ratios:

⇔ In ΔABC, ∠ABC = 90° and ∠ACB = θ.

 

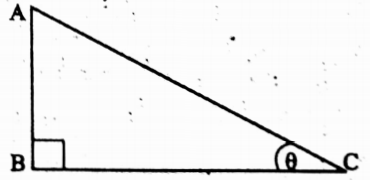
⇔ sin θ = \(\frac{\text { perpendicular }}{\text { hypotenuse }}=\frac{\mathrm{AB}}{\mathrm{AC}}\)

⇔ cos θ = \(\frac{\text { base }}{\text { hypotenuse }}=\frac{\mathrm{BC}}{\mathrm{AC}}\)

⇔ tan θ = \(\frac{\text { perpendicular }}{\text { base }}=\frac{\mathrm{AB}}{\mathrm{BC}}\)

⇔ cosec θ = \(\frac{\text { hypotenuse }}{\text { perpendicular }}=\frac{\mathrm{AC}}{\mathrm{AB}}\)

⇔ sec θ = \(\frac{\text { hypotenuse }}{\text { base }}=\frac{\mathrm{AC}}{\mathrm{BC}}\)

⇔ cot θ = \(\frac{\text { base }}{\text { perpendicular }}=\frac{\mathrm{BC}}{\mathrm{AB}}\)

∴ sin θ = \(\frac{1}{cosec \theta}\)

Read and Learn More WBBSE Solutions for Class 10 Maths

⇒ sin θ.cosec θ = 1

⇔ cos θ = \(\frac{1}{sec \theta}\)

⇒ cos θ.sec θ = 1

⇔ tan θ = \(\frac{1}{cot \theta}\)

⇒ tan θ.cot θ = 1

WBBSE Notes For Class 10 Geography And Environment	WBBSE Notes For Class 10 History And Environment
WBBSE Solutions For Class 10 Life Science	WBBSE Class 10 Life Science Multiple Choice Questions
WBBSE Solutions for Class 10 Maths	WBBSE Class 10 Maths Multiple Choice Questions
WBBSE Notes For Class 10 Physical Science And Environment

 

⇔ \(\tan \theta=\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{\frac{\mathrm{AB}}{\mathrm{AC}}}{\frac{\mathrm{BC}}{\mathrm{CA}}}=\frac{\sin \theta}{\cos \theta}\)

⇔ \(\cot \theta=\frac{\cos \theta}{\sin \theta}\)

Class 10 Maths Trigonometry Chapter 2 Solutions

Some Trigonometric identities of an acute angle:

1. sin² θ+ cos² θ = 1
2. sec² θ= 1 + tan² θ
3. cosec² θ = 1 + cot² θ

Following tables gives the values of trigonometric ratios :

Trigonometry Chapter 2 Trigonometric Ratios And Trigonometric Identities True Or False

Example 1. The value of tan A is always greater than 1.

Solution:

 

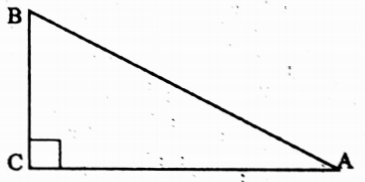
tan A = \(\frac{\mathrm{BC}}{\mathrm{AC}}\)

tan A = \(\frac{\mathrm{BC}}{\mathrm{BC}}\) [If BC = AC] = 1

tan A < 1 [If BC < AC]

tan A > 1 [If BC > AC]

So the statement is false.

Example 2. The value of cot A is always less tan 1.

Solution:

 

cot A = \(\frac{\mathrm{AC}}{\mathrm{BC}}\)

cotA = \(\frac{\mathrm{AC}}{\mathrm{AC}}\) [If AC = BC]

cot A = 1

cot A < 1 [If AC < BC]

cot A > 1 [If AC > BC]

∴ So the statement is false.

Wbbse Class 10 Maths Trigonometry Solutions

Example 3. For an angle θ, it may be possible that, sin θ = \(\frac{4}{3}\)

Solution:

 

sin θ = \(\frac{\mathrm{AB}}{\mathrm{AC}}\)

In a right-angled triangle hypotenuse is always greater than each of other two sides

∴ AB < AC  i.e. \(\frac{\mathrm{AB}}{\mathrm{AC}}\) < 1

∴ sin θ < 1

∴ The statement is false.

Example 4. For an angle α, it may be possible that, sec α = \(\frac{12}{5}\)

Solution:

 

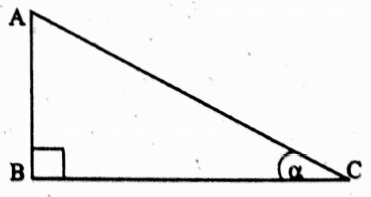
sec α = \(\frac{\mathrm{AC}}{\mathrm{BC}}\)

as AC > BC [hypotenuse > side]

i.e. \(\frac{\mathrm{AC}}{\mathrm{BC}}\) > 1  ∴ sec α > 1

∴ The statement is true.

Heights And Distances Class 10 Solutions

Example 5. For an angle β, it may be possible that, cosec β= \(\frac{5}{13}\)

Solution:

 

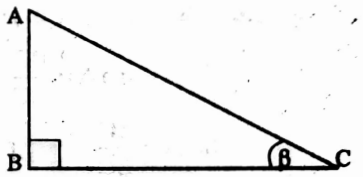
cosec β = \(\frac{\mathrm{AC}}{\mathrm{AB}}\)

and AC > AB i.e. \(\frac{\mathrm{AC}}{\mathrm{AB}}\) > 1 ∴ cosec β > 1

∴ The statement is false.

Example 6. For an angle θ, is may be possible that, cos θ = \(\frac{3}{5}\)

Solution:

 

cos θ = \(\frac{\mathrm{BC}}{\mathrm{AC}}\)

BC < AC

i.e, \(\frac{\mathrm{BC}}{\mathrm{AC}}\) < 1 ∴ cos θ < 1

∴ The statement is true.

Example 7. If 0° ≤ α ≤ 90°, then the least value of (sec² α + cos² α) is 2.

Solution: sec² α + cos² α

= \(\frac{1}{\cos ^2 \alpha}+\cos ^2 \alpha\)

= \(\left(\frac{1}{\cos \alpha}-\cos \alpha\right)^2+2 \cdot \frac{1}{\cos \alpha} \cdot \cos \alpha\)

= \(\left(\frac{1}{\cos \alpha}-\cos \alpha\right)^2+2\)

\(\text { as } 0^{\circ} \leq \alpha \leq 90^{\circ}\)

 

∴ \(\left(\frac{1}{\cos \alpha}-\cos \alpha\right)^2 \geq 0\)

∴ The lease value of (sec² α + cos² α)

∴ The statements is true.

Example 8. The value of (cos 0° x cos 1° x cos 2° x cos 3° x…..x cos 90°) is 1.

Solution: (cos 0° x cos 1° x cos 2° x cos 3° x …… x cos 90°)

= cos 0° x cos 1° x cos 2° x ……. x 0 = 0

∴ The statement is false.

Class 10 Trigonometry Chapter 2 Solved Examples

Trigonometry Chapter 2 Trigonometric Ratios And Trigonometric Identities Fill In The Blanks

Example 1. The value of \(\left(\frac{4}{\sec ^2 \theta}+\frac{1}{1+\cot ^2 \theta}+3 \sin ^2 \theta\right)\) is ________

Solution: \(\frac{4}{\sec ^2 \theta}+\frac{1}{1+\cot ^2 \theta}+3 \sin ^2 \theta\)

= 4 cos² θ + \(\frac{1}{cosec^2 \theta}\) + 3sin² θ

= 4 cos² θ + sin² θ + 3 sin² θ = 4 cos² θ + 4 sin² θ

= 4 (cos² θ + sin² θ) = 4 x 1 =4

∴ Answer is 4.

Example 2. If sin (θ – 30°) = \(\frac{1}{2}\), then the value of cos θ is ______

Solution: sin (θ – 30°) = \(\frac{1}{2}\)

⇒ sin (θ – 30°) = sin 30°

⇒ θ – 30° = 30° ⇒ θ = 60°

cos θ = cos 60° = \(\frac{1}{2}\)

∴ Answer is \(\frac{1}{2}\)

Example 3. If cos² θ – sin² θ = \(\frac{1}{2}\), then the value of cos⁴ θ – sin⁴ θ is _______

Solution: cos⁴ θ- sin⁴ θ

= (cos² θ)² – (sin² θ)²

= (cos² θ + sin² θ) (cos² θ – sin² θ)

= 1 x \(\frac{1}{2}\) = \(\frac{1}{2}\)

∴ Answer is \(\frac{1}{2}\)

Wbbse Class 10 Trigonometry Notes

Example 4. The value of \(\left(\sin \frac{\pi}{3} \cos \frac{\pi}{6}+\cos \frac{\pi}{3} \sin \frac{\pi}{6}\right)\) is _____

Solution: sin\(\frac{\pi}{3}\)cos\(\frac{\pi}{6}\)+ cos\(\frac{\pi}{3}\)sin\(\frac{\pi}{6}\)

= sin\(\frac{180^{\circ}}{3}\)cos\(\frac{180^{\circ}}{6}\) + cos\(\frac{180^{\circ}}{3}\)sin\(\frac{180^{\circ}}{6}\)

= sin 60° cos 30° + cos 60° sin 30°

= \(\frac{\sqrt{3}}{2}\) x \(\frac{\sqrt{3}}{2}\) + \(\frac{1}{2}\) x \(\frac{1}{2}\) = \(\frac{3}{4}\) + \(\frac{1}{4}\) = 1

∴ Answer is 1.

Example 5. If a cos θ = 4 and a sec θ = 9, then the value of a is _______

Solution: a cos θ.a sec θ = 4 x 9

⇒ a² x 1 = 36

⇒ a = ± 6

∴ Answer is ± 6.

Angle Of Elevation And Depression Class 10 Solutions

Trigonometry Chapter 2 Trigonometric Ratios And Trigonometric Identities Short Answer Type Questions

Example 1. If r cos θ = 2√3, r sin θ = 2, and 0° < θ < 90°, then determine the value of both r and θ.

Solution: r cos θ = 2√3

r sin θ = 2

r² cos² θ + r² sin² θ = (2√3)² + (2)²

⇒ r² (cos² θ + sin² θ) = 12 + 4

⇒ r² x 1 = 16  ⇒ r = √16 = 4

r sin θ = 2

4 sin θ = 2

⇒ sin θ = \(\frac{2}{4}\) = \(\frac{1}{2}\)

⇒ sin θ = sin 30° ⇒ θ = 30°

∴ r = 2, θ = 30°

Example 2. If sin A + sin B = 2 where 0° ≤ A ≤ 90° and 0° ≤ B ≤ 90°, then find out the value of (cos A + cos B)

Solution: sin A + sin B = 2 = 1 + 1

⇔ sin A + sin B = sin 90° + sin 90°

⇔ sin A = sin 90°

⇔ A = 90°

⇔ Sin B = sin 90°

⇔ B = 90°

⇔ cos A + cos B = cos 90° + cos 90° = 0 + 0 = 0

Example 3. If 0° < θ < 90°, then calculate the least value of (9 tan² θ + 4 cot² θ).

Solution: 9 tan² θ +4 cot² θ

= (3 tan θ)² + (2 cot θ)²

= (3 tan θ – 2 cot θ)² + 2.3 tan θ.2 cot θ

= (3 tan θ- 2 cot θ)² + 12.1 [tan θ = 1/cot θ]

= (3 tan θ – 2 cot θ)² + 12

⇔ The least value of any perfect square of the expression is 0 (zero).

⇔ So, the least value of (3 tan θ – 2 cot θ) is zero.

∴ The least value of (9 tan² θ + 4 cot² θ) is 12.

Example 4. Calculate the value of (sin⁶ α + cos⁶ α + 3 sin²α + cos²α ).

Solution: sin⁶α + cos⁶α + 3 sin²α cos²α

= (sin²α)³ + (cos²α)³ + 3 sin²α cos²α

= (sin²α + cos²α)³ – 3.sin²α cos²α (sin²α + cos²α) + 3 sin²α cos²α

= (1)³ – 3 sin²α cos²α (1) + 3 sin²α cot²α

= 1-3 sin²α cos²α + 3 sin²α cos²α = 1

Example 5. If cosec² θ = 2 cot ² θ and 0° < θ < 90°, then determine the value of θ.

Solution: cosec² θ = 2 cot θ

⇒ 1 + cot² θ = 2 cot θ

⇒ cot² θ – 2 cot θ + 1 = 0

⇒ (cot θ – 1)² = 0  ⇒ cot θ – 1 = 0 ⇒ cot θ = 1

⇒ cot θ = cot 45° ⇒ θ = 45°

Class 10 Maths Trigonometry Important Questions

Example 6. If \(\frac{\cos \theta+\sin \theta}{\cos \theta-\sin \theta}=\frac{\sqrt{3}+1}{\sqrt{3}-1}\) then find the value of

Solution: \(\frac{\cos \theta+\sin \theta}{\cos \theta-\sin \theta}=\frac{\sqrt{3}+1}{\sqrt{3}-1}\)

⇒ \(\frac{\cos \theta+\sin \theta+\cos \theta-\sin \theta}{\cos \theta+\sin \theta-\cos \theta+\sin \theta}=\frac{\sqrt{3}+1+\sqrt{3}-1}{\sqrt{3}+1-\sqrt{3}+1}\) [By componendo-dividend process]

⇒ \(\frac{2 \cos \theta}{2 \sin \theta}=\frac{2 \sqrt{3}}{2}\)

⇒ \(\cot \theta=\sqrt{3}\)

⇒ cot θ = cot 30°

⇒ θ = 30°

Example 7. If \(\tan ^2 \frac{\pi}{4}-\sin ^2 \frac{\pi}{6}=x \sec ^2 \frac{\pi}{4} \cos ^2 \frac{\pi}{3}\) then find the value of x.

Solution: \(x \sec ^2 \frac{\pi}{4} \cos ^2 \frac{\pi}{3}=\tan ^2 \frac{\pi}{4}-\sin ^2 \frac{\pi}{6}\)

⇒ \(x \sec ^2 45^{\circ} \cos ^2 60^{\circ}=\tan ^2 45^{\circ}-\sin ^2 30^{\circ}\)

⇒ \(x \times(\sqrt{2})^2 \times\left(\frac{1}{2}\right)^2=(1)^2-\left(\frac{1}{2}\right)^2\)

⇒ x x 2 x \(\frac{1}{4}\) = 1 – \(\frac{1}{4}\)

⇒ \(\frac{x}{2}\) = \(\frac{3}{4}\)

⇒ x = \(\frac{3}{2}\)

Example 8. If tan θ + sin θ = a and tan θ – sin θ = b, then find the value of \(\frac{a^2-b^2}{\sqrt{a b}}\)

Solution: a² – b² = (tan θ + sin θ)² – (tan θ – sin θ)²

= 4 tan θ.sin θ

\(\sqrt{a b}=\sqrt{(\tan \theta+\sin \theta)(\tan \theta-\sin \theta)}=\sqrt{\tan ^2 \theta-\sin ^2 \theta}\)

= \(\sqrt{\frac{\sin ^2 \theta}{\cos ^2 \theta}-\sin ^2 \theta}\)

= \(\sqrt{\sin ^2 \theta\left(\frac{1}{\cos ^2 \theta}-1\right)}=\sin \theta \sqrt{\frac{1-\cos ^2 \theta}{\cos ^2 \theta}}\)

= \(\sin \theta \cdot \sqrt{\frac{\sin ^2 \theta}{\cos ^2 \theta}}=\sin \theta \cdot \sqrt{\tan ^2 \theta}=\sin \theta \cdot \tan \theta\)

\(\frac{a^2-b^2}{\sqrt{a b}}=\frac{4 \sin \theta \tan \theta}{\sin \theta \cdot \tan \theta}=4\)

Class 10 Maths Trigonometry Important Questions

Example 9. If a sinθ + b cosθ = c, then find the value of (a cosθ – b sinθ).

Solution: a sinθ+ b cosθ = c

⇒ (a sinθ + bcosθ)² = c²

⇒ a² sin² θ + b² cos² θ + 2ab sinθcosθ= c²

⇒  a² (1 – cos² θ) + b² (1 – sin² θ) + 2ab si θ cosθ = c²

⇒ a² – a² cos² θ + b² – b² sin² θ + 2ab sinθ cosθ = c²

⇒ a² + b² – c² = a² cos² θ+ b² sin² θ- 2ab cosθ sinθ

⇒ a² + b² – c² = (acosθ – bsinθ)²

⇒ acosθ – bsinθ = ± \(\sqrt{a^2+b^2-c^2}\)

Example 10. If x = a sinθ and y = b tanθ, then find the value of \(\left(\frac{a^2}{x^2}-\frac{b^2}{y^2}\right)\).

Solution: a sinθ = x

⇒ \(\frac{a}{x}=\frac{1}{\sin \theta}={cosec} \theta\)

b tan θ = y

⇒ \(\frac{b}{y}=\frac{1}{\tan \theta}=\cot \theta\)

⇒ \(\frac{a^2}{x^2}-\frac{b^2}{y^2}={cosec}^2 \theta-\cot ^2 \theta=1\)

Example 11. If 0° < θ< 90° and 2 cos² θ + 3 sinθ = 3 then find the value of θ.

Solution: 2 cos² θ+ 3 sinθ = 3

⇒ 2 (1 – sin² θ) + 3 sinθ= 3

⇒ 2-2 sin² θ + 3 sinθ = 3

⇒ 2 sin² θ – 3 sinθ + 1 = 0

⇒ 2 sin² θ – 2 sinθ – sinθ + 1 = 0

⇒ 2 sinθ (sinθ – 1) – 1 (sinθ – 1) = 0

⇒ (sinθ – 1) (2 sinθ – 1) = 0

either sinθ – 1 =0

⇒ sinθ = 1

2 sinθ – 1 = 0

⇒ 2 sinθ = 1

⇒ sinθ = sin90°

⇒ sinθ = \(\frac{1}{2}\)

⇒ θ = 90°

⇒ sinθ = sin 30°

⇒ θ = 30°

As 0° < θ < 90°

∴ The value of θ is 30°

Example 12. If θ is positive acute angle then find the least value of (25 sec² θ + 49 cos² θ)

Solution: (25 sec² θ + 49 cos² θ)

= (5 secθ)² + (7 cosθ)²

= (5 secθ – 7 cosθ)² + 2.5 secθ 7 cosθ

=(5secθ -7cosθ)² +70secθ.\(\frac{1}{\sec \theta}\)

= (5 secθ – 7 cosθ)² + 70

(5 secθ – 7 cosθ)² ≥ 0

∴ Least value of (25 sec² θ + 49 cos² θ) is 70.

Example 13. If sinθ + sin² θ + sin³ θ = 1 then find the value of (cos⁶ θ- 4 cos⁴ θ + 8 cos² θ).

Solution: sinθ+ sin² θ+ sin³ θ = 1

⇒ sinθ + sin³ θ = 1 – sin² θ

⇒ sinθ (1 + sin² θ) = cos² θ

⇒ sin² θ (1 + sin² θ)² = cos⁴ θ [squaring both side]

⇒ (1 – cos² θ) (1 + 1 – cos² θ)² = cos⁴ θ

⇒ (1 -cos² θ) (2 – cos² θ)² = cos⁴ θ

⇒ (1- cos² θ) (4 – 4 cos² θ + cos⁴ θ) = cos⁴ θ

⇒ 4 – 4 cos² θ + cos⁴ θ – 4 cos² θ + 4 cos⁴ θ- cos⁶ θ = cos⁴ θ

⇒ cos⁶ θ – 4 cos⁴ θ + 8 cos² θ = 4

Class 10 Maths Trigonometry Chapter 2 Solutions

Example 14. In ΔABC each angle is a positive acute angle. If cos (B + C – A) = 0 and sin (C + A – B) = \(\frac{\sqrt{3}}{2}\), then find the value of A, B, and C.

Solution: cos (B + C – A) = 0

⇒ cos (B + C – A) = cos 90°

⇒ B + C – A = 90° ……(1)

sin (C + A – B) = \(\frac{\sqrt{3}}{2}\)

⇒ sin (C + A – B) = sin 60°

⇒ C + A- B = 60° ……..(2)

(1) + (2), we get

B + C- A + C + A- B= 90° + 60°

⇒ 2C = 150°  ⇒ C = 75°

From (2), 75° + A -B = 60°

⇒ A – B = – 15°……(3)

Again, In ΔABC,

A + B + C = 180°

A + B + 75° = 180°

⇒ A + B = 105°….(4)

A + B + A- B = 105°- 15°

⇒ 2A = 90°

⇒  A = 45°

∴ B = 105° – 45° = 60°.