WBBSE Solutions For Class 10 Physical Science And Environment Chapter 4 Thermal Phenomena

WBBSE Chapter 4 Thermal Phenomena Thermal Expansion Expansion of solids from everyday experience

A tightly fitted metal cap on a bottle can be loosened by heating the neck of the bottle. On heating, the metal cap expands and it gets space to be loosened.

While laying railway tracks, if the rails are placed end to end, they may bend due to expansion in summer and it may cause accidents.

To avoid it, small gaps are left between two successive rails to allow them to expand for expansion

Wbbse Class 10 Physical Science Notes

Telephone wires and electric wires are always kept sagging to prevent their snapping when they contract in winter Almost all substances, whether solid, liquid, or gas, expand on heating

There are a few exceptions to the rule: water from 0°C to 4°C, and silver iodide from 20°C to 141°C.

And contract on cooling Such expansion of any substance on heating is known as thermal expansion.

WBBSE Notes For Class 10 Physical Science And Environment

A solid has a definite shape. So when a solid is heated, it expands in all directions, without any change in its mass. That is, on heating, the length, surface area, and volume of a solid all increase. Thus there are three kinds of thermal expansion in the case of solids:

1. Linear Expansion,
2. Superficial or surface Expansion and
3. Cubical or volume Expansion.

On heating, the increase in the length of a solid is called linear expansion, the increase in surface area is called surface expansion, and the increase in volume is called volume expansion.

The liquids and gases do not have a definite length, area, or shape, but they have a definite volume. So, liquids and gases have only volume expansion.

Wbbse Class 10 Physical Science Notes

As the molecules in solids are very tightly packed, so thermal expansion of solids is very small.

Apparently, it is difficult to understand such a small thermal expansion. Through experiments, it can be proved.

Bar and gauge experiment: Let us take a bar and a gauge set-up which consists of a metal bar and a metal gauge.

When both of these two are at room temperature, the bar just fits into the gap in the gauge. But when the bar is heated using a burner, it does not fit into the gap in the gauge.

This happens because the bar expands on heating and becomes longer in size than the gap in the gauge.

If the bar is then allowed to cool down to room temperature, after some time it is seen that the bar again fits into the gap in the gauge. This happens because the bar contracts on .pooling.

Thus, the bar and gauge set-up proves the thermal expansion of solid by heating and contraction by cooling.

Bimetallic strip experiment: Let us take a bimetallic strip, made up of two strips of different materials, such as brass and iron, having the same dimensions placed one over another lengthwise and properly riveted at their ends.

At room temperature, the bimetallic strip is straight. Using a burner, when the bimetallic strip is heated the strip bends with the brass portion on the outer side.

Wbbse Class 10 Physical Science Notes

The experiment proves that brass expands more than iron for the same rise in temperature. If the strip is cooled (even below room temperature) brass contracts more than iron.

Bimetallic strips are used in electrical heating devices like electric irons, geysers, ovens, refrigerators, toasters, etc.

where power gets cut off automatically as soon as the temperature reaches a desired value.

On heating, the increase in the length of a solid is called linear expansion, the increase in surface area is called surface expansion, and the increase in volume is called volume expansion.

The liquids and gases do not have a definite length, area, or shape, but they have a definite volume. So, liquids and gases have only volume expansion.

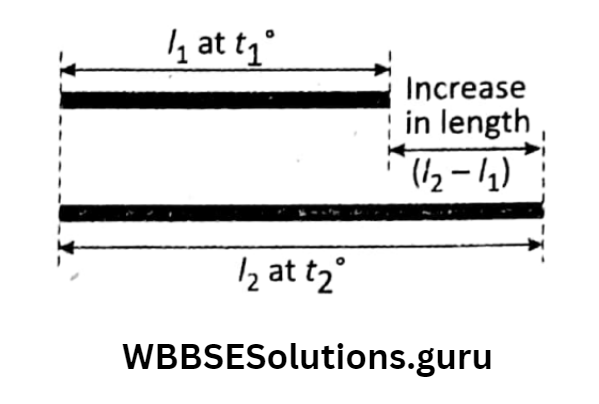
Let us take a thin rod of length at the initial temperature On heating the rod through let the final length become So, the increase in length = \(\left(I_2-I_1\right)\) for the increase in temperature

=\(\left(t_2-t_1\right)\) By experiments, it is found that the increase in length of a rod is—

1. Directly proportional to its original length, if the increase, at tx in temperature is not very large.

That is  \(\left(I_2-I_1\right) \propto I_1 \ldots\) And

2. Directly proportional to its original length, if the increase in temperature, is not very large. that is

⇒ \(\left(I_2-I_1\right)\)\(\propto\left(t_2-t_1\right)\)

[where α is a constant of proportionality and it is called the Si ‘coefficient of surface expansion’]

Combining (1) And (2)

⇒ \(\left(I_2-I_1\right) \propto I_1\left(t_2-t_1\right)\)

or \(\left(I_2-I_1\right)=I_1 \cdot \alpha \cdot\left(t_2-t_1\right)\)

or, \(\alpha=\frac{I_2-I_1}{I_1\left(t_2-t_1\right)}\)

i.e., Coefficient of linear expansion=\(\frac{\text { Increase in length }}{\text { Original length } \times \text { Rise in temperature }}\)

⇒ \(\text { If } I_1=1 \text { and } t_2-t_1=1 \text { then } \alpha=\left(I_2-I_1\right) \text {. }\)

Physics Class 10 Wbbse

Definition: The coefficient of linear expansion of a solid is the increase in length per unit original of a solid is the increase in length per unit original length per unit degree rise in temperature.

Units of \(\alpha\): In the CGS system it is per °C  or °C ^–¹; and in S.l. The system, per K or K^–¹.

As the part Length in length/original length is unless and dimensionless, the coefficient of linear expansion does not depend on the unit of length; it depends only on the unit of temperature.

For example = \(\alpha=12 \times 10^{-6 \circ} \mathrm{C}^{-1}\) means that the length of an iron rod of initial length 1 m increases by 12 x 10^-6 m on increasing its temperature by 1°C.

Similarly, \(\alpha=17 \times 10^{-6}{ }^{\circ} \mathrm{C}^{-1}\) for copper means that the length of a copper rod of initial length increases by 17 x 10^-6 m on increasing its temperature by 1°C.

Wbbse Class 10 Physical Science Notes

Thus, iron expands less than copper for the same rise in temperature. shows that different materials have different thermal expansion means different materials expand differently for increasing temperature by 1°C.

WBBSE Chapter 4 Thermal Phenomena Coefficient Of Surface Expansion

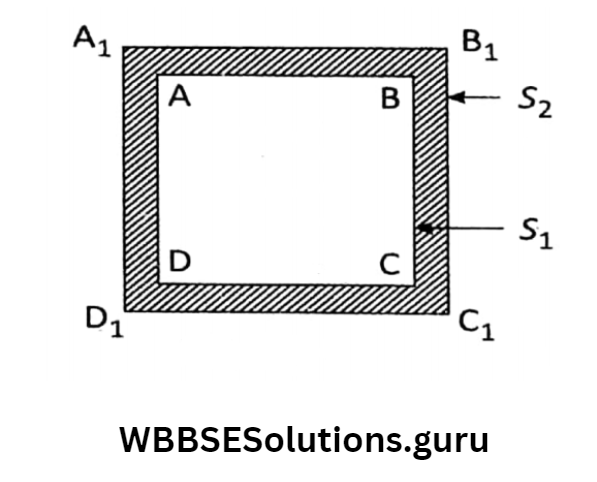
Let us take a thin plate (two-dimensional object) of initial area S₁ at temperature tr When it is heated through t₂, suppose the final area becomes S₂. So, the increase in the area
= (S₂– S₁)for the increase in temperature = (t₂ – t₁).

As in the case of linear expansion, here also we can get, S₂ (S₂ – S₁) = S₁. β. (t₂ – t₁) [where β is a constant of proportionality and it is called the Si ‘coefficient of surface expansion’]

or, \(\beta=\frac{S_2-S_1}{S_1\left(t_2-t_1\right)}\)

i.e., Coefficient of surface expansion =\(\frac{\text { Increase in surface area }}{\text { Original surface area } \times \text { Rise in temperature }}\)

Definition: The coefficient of surface expansion is the increase in surface area per unit of original surface area per unit degree rise in temperature.

Units of β: In the CGS system °C^-1 and in S.l. system K^-1.

Physics Class 10 Wbbse

The meaning of the statement \(\beta=24 \times 10^{-6}{ }^{\circ} \mathrm{C}^{-1}\)  for iron is that the area of an iron plate of an initial area of 1 m₂ increases by 24

WBBSE Chapter 4 Thermal Phenomena Coefficient Of Volume

Let us take a metal like a cube, sphere, cylinder, or cone (three-dimensional object) of initial volume V₁ at temperature t₂ When it is heated through t₂, its final volume becomes V₂. So, the increase in volume = (V₂ – V₁) for the increase in temperature through (t₂-t₁).

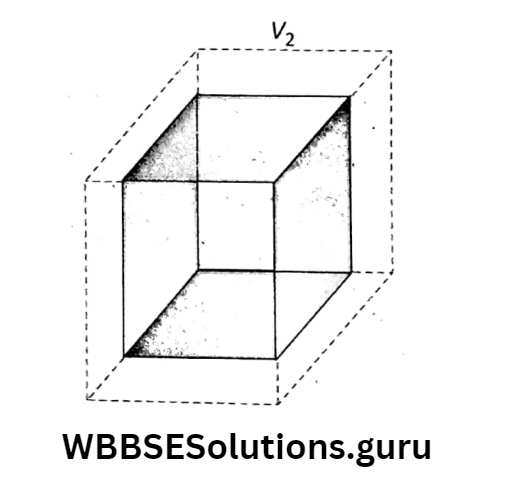
Similarly, in this case, we can get,  [where γ is a constant of proportionality and it is called ‘coefficient of volume expansion, or,  \(\gamma=\frac{V_2-V_1}{V_1\left(t_2-t_1\right)}\)

i.e., Coefficient of cubical expansion = \(\frac{\text { Increase in volume }}{\text { Originalvolume } \times \text { Rise in temperature }}\)

If \(V_1=1 \text { and }\left(t_2-t_1\right)=1 \text { then } \gamma=\left(V_2-v_1\right) \cdot \gamma=36 \times 10^{-6}{ }^{\circ} \mathrm{C}^{-1}\)

for iron means that if we have a three-dimensional object of iron of volume lm3 and if its temperature is increased by 1°C its volume will increase by \(36 \times 10^{-6} \mathrm{~m}^3\)

Definition: The increase in volume per unit original volume per unit degree rise in temperature is called the coefficient of volume expansion of the substance.

Physics Class 10 Wbbse

WBBSE Chapter 4 Thermal Phenomena Thermal Expansion Of Liquids

Did you notice that the level of mercury in a thermometer rises when it is placed in hot water? Why does this happen?

Actually, the mercury inside the thermometer takes heat from hot water and expands. So like solids, liquids also expand on heating.

In liquids, molecules are less tightly bound as compared to solids, and therefore, liquids expand much more than solids for a given rise in temperature.

A liquid has no definite shape and it is always contained in a vessel. So, when a liquid is heated, only its change in volume occurs.

The vessel also expands along with the liquid. Suppose, in the experimental set-up, the initial level of water is at A (before heating) inside the capillary tube. Placing the flask in hot water, the flask expands and it is seen that—

First of all, the level of water falls from point A to point B. So, V_AB represents an expansion of vessels,

After a few minutes, the level of water starts rising. It not only reaches A but overcoming A further reaches up to point C.

So, V_BC  represents a real expansion of the liquid. Practically we don’t see the expansion of vessels. That is, the expansion of the vessel is to be taken into account for measuring real expansion.

It appears to us that liquid expands from point A to point C. So, V_AC represents the apparent expansion of the liquid.

i.e., Real expansion of liquid = Apparent expansion of liquid + Expansion of the vessel.

Thus, in the case of the thermal expansion of liquids, we are to consider both the appearance as well as real expansion.

This means that there are two types of expansion coefficients for a liquid. These are

Coefficient of real expansion and The Coefficient of apparent expansion.

Physics Class 10 Wbbse

Coefficient of real expansion: Let the initial volume of a fixed amount of a liquid at a temperature t₁ be V₁ and at a temperature t₂ the real volume becomes V₂ (where t₂ > t₁).

So, by definition, \(\gamma_r=\frac{V_2-V_1}{V_1\left(t_2-t_1\right)}=\frac{\text { Real increase in volume }}{\text { Initial volume of liquid } \times \text { Rise in temperature }}\)

Definition: The coefficient of real expansion of a liquid is the real increase in volume per unit initial volume per degree rise in temperature.

The S.l. unit γ_r is K^-1.

(2) let for the same rise in temperature, the apparent volume of the liquid be V₂‘.

So, by definition: \(V_a=\frac{V_2^{\prime}-V_1}{V_1\left(t_2-t_1\right)}=\frac{\text { Apparent increase in volume }}{\text { Intial volume of liquid } \times \text { Rise in temperature }}\)

Definition: The coefficient of apparent expansion of a liquid is the apparent increase in volume per unit initial volume per degree rise in temperature.
The S.I. unit γ_a is K^-1.

Relationship: Coefficient of real expansion of liquid = Coefficient of apparent expansion of liquid + Coefficient of volume expansion of the vessel.

i.e., \(\gamma_r=\gamma_a+\gamma_g\)

Physics Class 10 Wbbse

It is important that the coefficient of real expansion is the intrinsic property of a liquid and it never depends on the material of the vessel.

WBBSE Chapter 4 Thermal Phenomena Thermal expansion of gases

Gases also expand on heating. In fact, gases expand much more than solids or liquids as the molecules in a gas are very loosely bound as compared to solids or liquids.

For example, if we keep a gas balloon in the sun or heat it, we will see that the balloon expands gradually in volume and finally bursts out.

This happens because the gas inside the balloon expands so fast that the expansion of the balloon (container) is not comparable with the expansion of gas.

So, we can neglect the expansion of the container in case of thermal expansion of gas. Here there is no apparent expansion, there is only real expansion.

By changing the temperature for a given sample of gas both the volume and pressure change. So gas can be heated in two ways—

either by keeping its pressure constant or by keeping its volume constant. When a gas is heated keeping the pressure constant, its volume increases, and when a gas is heated keeping the volume constant, its pressure increases.

Due to this fact, gases usually have two types of expansion coefficients—

1. Volume coefficient and
2. Pressure coefficient. Here we will discuss the volume coefficient only.

Definition: The coefficient of volume expansion of a fixed mass of gas at constant pressure (γ_p) is the increase in its volume per unit volume when the temperature is increased by 1°C from 0°C.

Unit  If V₀ and V_t are the respective volumes of the gas concerned under constant pressure then
to Charles’ law, at constant pressure,

the change in volume of a given sample of gas with the by definition, volume coefficient \(\gamma_p=\frac{V_t-V_0}{V_0 t} \text { or, } V_t-V_0=V_0 \gamma_p t \text { or, } V_t=v_0\left(1+\gamma_p t\right)\)

According to Charles’ law, at constant pressure, the change in volume of a given sample of gas with the increase in temperature is a Change in temperature i.e.,

= \(\frac{\text { Volume of gas at } 0^{\circ} \mathrm{C}}{273} \times \text { Change in temperature }\)

⇒ \(V_t-V_0=\frac{V_0}{273} \times t \text { or, } V_t=V_0\left(1+\frac{t}{273}\right) \ldots\)

(1) Comparing and (2) \(\text { we get : } \gamma_p=\frac{1}{273}{ }^{\circ} \mathrm{C}^{-1} \text {. }\)

Physics Class 10 Wbbse

WBBSE Chapter 4 Thermal Phenomena Thermal Conduction Thermal Conductivity

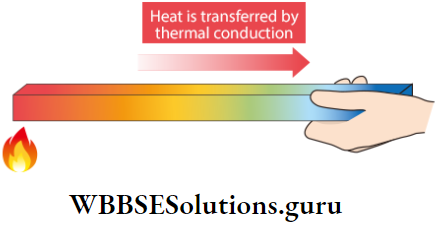
If we hold a steel spoon over the flame of a candle, the spoon first gets warm, then hot, and finally so hot, that we will not be able to hold it. Such a method of transmission

of heat from the hot end to the cold end of a solid by molecular collisions without the actual movement of the particles is called conduction.

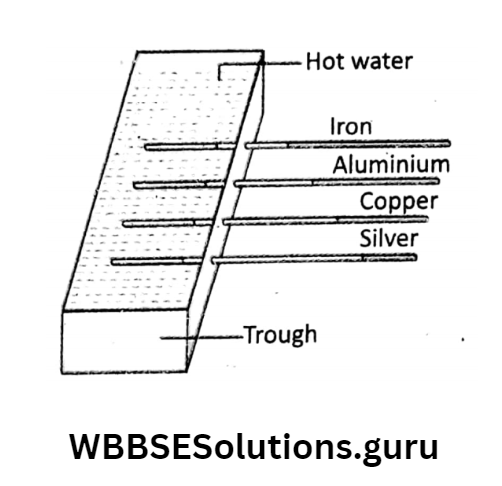
Different substances conduct heat differently (Ingen Hauz’s experiment: four metallic rods (say, iron, aluminium, copper and silver) of equal shape and size, dipping into molten wax, are fitted into
the holes on one side of a trough. Fill the trough with hot water.

It is observed that as heat is conducted through the rods, wax coatings over the rods start melting. Wax melts to different lengths in different rods although they are heated identically.

It proves that the ability to conduct heat is different for different substances. Generally, metals such as silver, copper, gold, aluminium, mercury, etc. are good conductors of heat as they allow heat to pass through them faster. On the other hand, substances such as glass, air, wool, paper, clay, etc.

Are bad conductors and insulators of heat as they do not allow heat to pass through them easily. They provide good insulation.

All liquids (except mercury) and gases are bad conductors of heat..

Examples of thermal conductivity from everyday experience:

(1) Did you know why cooking utensils are made of copper or aluminium? Because of their high value of thermal conductivity.

(2) Same reason why kettles are usually made of aluminium.

(3) Ice is covered with sawdust to prevent melting. Because sawdust itself is a bad conductor and this traps a lot of air—

which is also a bad conductor. So, heat from outside cannot reach the ice block. Heat is conducted normally along the length of the rod.

As a result, each layer of a cross-section of the rod absorbs heat from its previous layer and transmits a part to the next layer.

Here assume that no heat is lost by radiation (suppose the steady-state rock is wrapped with some insulating material).

In this way, the temperature of each layer changes with respect to time. This goes on for some time and this state is known as the variable state.

Physics Class 10 Wbbse

But after a sufficient time, the temperature of each cross section comes to be constant with respect to time not with respect to length means heat passing through each layer is the same but the temperature is not the same throughout the whole rod.

This state is called the steady state. We should study steady state in case of discussing thermal conductivity.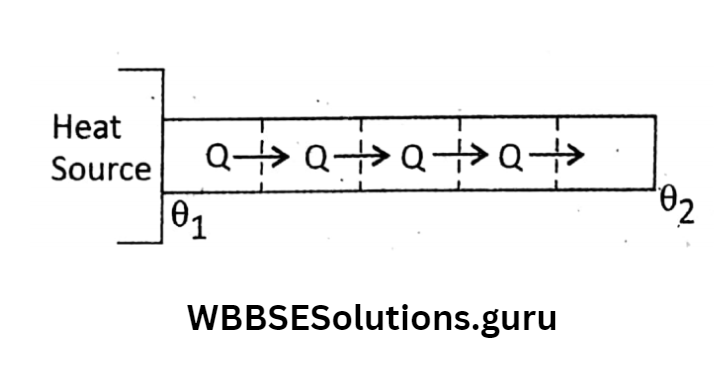Measurement of thermal conductivity: The thermal conductivity of a solid is a measure of the ability of a conductor to conduct heat through it.

Let us take a rectangular conducting bar or a cylindrical block of a thickness (length) d and

area of cross-section A. If temperatures at two different faces (ends) are θ₂ and θ₂ (θ₁ > θ₂), then during steady-state heat flows

normally from the hotter face to the colder face. In the steady state it has been found from experiments that the amount of heat (Q) that flows in time f depends on the following factors:

1. Area of cross-section (A),
2. Thickness (d),
3. The temperature difference between the faces (θ₁ – θ₂) and
4. The time of heat conduction (t).
5. Experimentally it is observed that
6. Mathematically,

Where K is a constant of proportionality. The value of constant K depends on the nature of the substance.

It is called the coefficient of thermal conductivity or simply thermal conductivity. K is different for different substances.

Ex. for wood K is very low but for Cu, it is considerably high. For an ideal conductor, K is infinity and for an ideal insulator, K is zero. It is a characteristic property of the substance.

Definition: In the equation Thus, for a conducting slab of unit area of cross-section and unit thickness, if the temperature difference between its two sides is 1° then the amount of heat flow from the hot side to the cold side in unit time is called the thermal conductivity of the substance.

Physics Class 10 Wbbse

1. Q α A,
2. Q α 1/d,
3. Q α (θ₁-θ₂)
4. Q α t

⇒ \(\text { Mathematically, } Q \propto A \cdot \frac{\theta_1-\theta_2}{d} \cdot t \quad \text { or, } Q=K \cdot A \cdot \frac{\theta_1-\theta_2}{d} \cdot t\)

Where K is a constant of proportionality. The value of constant K depends on the nature of the substance.

It is called the coefficient of thermal conductivity or simply thermal conductivity. K is different for different substances.

Ex. for wood K is very low but for Cu, it is considerably high. For an ideal conductor, K is infinity and for an ideal insulator, K is zero. It is a characteristic property of the substance.

Definition: In the equation if A = 1, d = 1, (θ_X – θ₂) = 1 and t = 1 then K= Q.

Thus, for a conducting slab of unit area of cross-section and unit thickness, if the temperature difference between its two sides is 1° then the amount of heat flow from the hot side to the cold side in unit time is called the thermal conductivity of the substance.

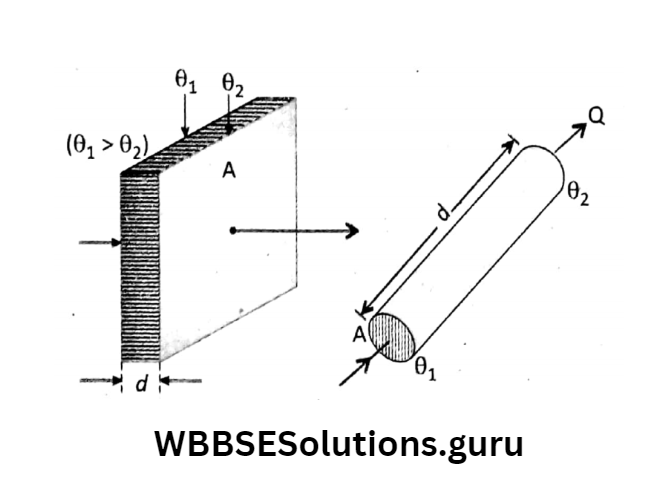Units of K: \(\text { As } Q=K \cdot A \cdot \frac{\theta_1-\theta_2}{d} \cdot t \text {, so that } K=\frac{Q \cdot d}{A\left(\theta_1-\theta_2\right) t} \text {. }\)

In the CGS system: The common unit of thermal conductivity (K) is cal x cm

= \(\frac{\mathrm{cal} \times \mathrm{cm}}{\mathrm{cm}^2 \times{ }^{\circ} \mathrm{C} \times \mathrm{s}}=\mathrm{cal} \cdot \mathrm{cm}^{-1}{ }^{\circ} \mathrm{C}^{-1} \cdot \mathrm{s}^{-1}\)

In Sl system: The unit of K is \(=\frac{\mathrm{J} \times m}{m^2 \times \mathrm{K} \times \mathrm{s}}=\mathrm{J} \cdot \mathrm{m}^{-1} \mathrm{~K}^{-1} \cdot \mathrm{s}^{-1}\)

= \(\mathrm{W} \cdot \mathrm{m}^{-1} \mathrm{~K}^{-1}\left[\text { as } \mathrm{J} \cdot \mathrm{s}^{-1}=\mathrm{W}\right. \text { ] }\)

Heat current (H): It is the flow of heat in unit time through a conductor. From the relation

Q = \(K A \frac{\theta_1-\theta_2}{d}\) we find that heat current,

H \(=\frac{\mathrm{Q}}{t}=\dot{\mathrm{KA}} \frac{\theta_1-\theta_2}{d}\)

From this relation, it is seen that the heat current depends on:

1. Area of cross-section (A) and temperature difference (G₁ – G₂) and thickness or length (d).

Thermal resistivity and its analogy with electrical resistivity: We know that the ‘potential difference’ between two ends of a conductor regulates the electric current, similarly, the ‘temperature difference’ between two sides of a conductor regulates the flow of heat current.

According to Ohm’s law, electric current = Rate of flow of electric charge \(=\frac{\text { Potential difference }}{\text { Electric resistance }} \text {. }\)

If V₁ and V₂ are the electric potentials (V₁ > V₂) at two ends of a conductor of resistance of R, then electric current, \(\mathrm{I}=\frac{q}{t}=\frac{V_1-V_2}{\mathrm{R}} \ldots \ldots\)

We get the relation for heat current,  \(\mathrm{H}=\frac{\mathrm{Q}}{t}=K A \frac{\theta_1-\theta_2}{d}=\frac{\theta_1-\theta_2}{\frac{d}{K \Delta}}\)

Comparing (1) And (2) we see that the quality \(\frac{d}{K A}\)

is equivalent to resistance \(\mathrm{R}_{\mathrm{Th}}\left(=\frac{d}{\mathrm{KA}}\right)\)

and it is called thermal resistance again from the relation between electrical resistance (R) and resistivity

R = \(\frac{\rho d}{A}\) [d being the length or thickness of the conductor and comparing

R=\(\frac{\rho d}{A} \text { with } R_{\text {Th }}=\frac{d}{K A}\) we find the term

∴ \(\frac{1}{K}\) as thermal resistivity of the conductor.