WBBSE Solutions For Class 10 Physical Science And Environment Chapter 6 Current Electricity

WBBSE Chapter 6 Current Electricity Electric Current, Potential Difference and EMF Concept Of Electric Charge

About 600 B.C., in ancient Greece, it was observed that rubbing of two substances acquired some special property of attracting light objects like small pieces of dry paper, light feathers, dry grass, etc. The reason was not known at that time.

A glass rod, rubbing with silk cloth, an ebonite rod rubbing with flannel (cat’s skin), or rubbing a plastic comb against dry hair or a balloon against woolen material, acquire the same kind of attractive properties.

The reason was explained by considering that the substances (comb, wool, balloon, glass, silk, etc.) become electrically charged on rubbing, as they have acquired electric charges.

Then the question arises—What is an electric charge?
Like mass, the charge is a fundamental (intrinsic) part of matter.

WBBSE Notes For Class 10 Physical Science And Environment

Charges exist in two forms— ‘positive’ and ‘negative’.

‘Positive’ and ‘negative’ are just names—used to indicate the existence of two types of charges. This charge convention was decided by Benjamin Franklin.

Each substance contains an equal amount of positive and negative charge. According to modern electronic theory, an atom has an equal number of protons and electrons (showing that an atom is electrically neutral). Charge of \(1 p=+1.6 \times 10^{-19} \mathrm{C} \text { and } 1 \mathrm{e}^{-}=-1.6 \times 10^{-19} \mathrm{C}\)

The transfer of electrons is the only cause responsible for the charging of the bodies.

If an atom gains electrons, it becomes negatively charged; and if an atom loses electrons, it becomes positively charged.

While rubbing two substances, the generated thermal energy initiates to transfer of electrons from one substance to another substance.

Wbbse Class 10 Physical Science Notes

This type of electricity is known as static electricity because there is no continuous motion of charges.

According to the law of conservation of charge, the charge can neither be created nor destroyed.

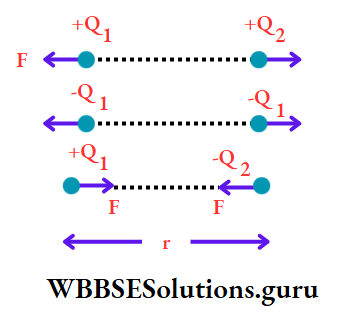
Coulomb’s law: Two like charges (either positive or negative) repel each other and two unlike charges (one positive charge and one negative charge) attract each other with a force known as an electric force.

Scientist Coulomb calculated the magnitude of the electric force acting between two charges. According to Coulomb, this force acts along the line joining two points charges.

Here ‘point charge’ refers to the charge of an object seen from a long distance.

Statement: In a particular medium, the force of attraction or repulsion between two point charges acting along the line joining the charges is directly proportional to the product of the charges and is inversely proportional to the square of the distance between them.

Referring to suppose two point charges and Q₂ are separated by a distance. The force acting between the charges is

⇒ \(F \propto Q_1 \cdot Q_2\) (when r is constant) and

⇒ \(F \propto \frac{1}{r^2}\) (When Q₁,Q₂ are Constant)

Or, F= \(k \cdot \frac{Q_1 Q_2}{r^2}\) (k is a constant of proportionality)

k is not a universal constant. The value of k depends on the nature of the medium. It is different for air, water, oil……..etc.

So the electric force between two point charges Q_1,Q₂ kept in different media would be \(F_{\text {air }}=\frac{k Q_1 Q_2}{r^2}, \quad F_{\text {water }}=\frac{k^{\prime} Q_1 Q_2}{r^2}, \quad F_{\text {oil }}=\frac{k^{\prime \prime} \mathrm{Q}_1 Q_2}{r^2} \ldots \ldots\)

Unit of charge: In the SI system, a unit of charge is the coulomb (C) and in the CGS system it is an electrostatic unit (esu) or statcoulomb (state).

Relation: 1 coulomb = 3 × 10⁹ esu Charge.

WBBSE Chapter 6 Current Electricity Electric Potential Difference

An electric field is said to exist around a charged particle within which it can exert an attractive or repulsive force.

Thus, the electric field is associated with each point in space around itself. If a second charge is brought within this electric field, an electric force acts on the charge.

Wbbse Class 10 Physical Science Notes

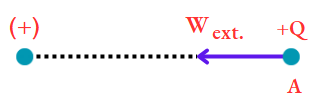
If the second charge is similar to that of the former, then work is to be done by an external agency against electric force.

And, if the charges are dissimilar, then electric force (i.e., attractive force) ownself does the work.

Definition: The amount of work done by an external agency in moving a unit positive charge from infinity to a point within an electric field, without any change of its K.E. is called the electric potential at that point.

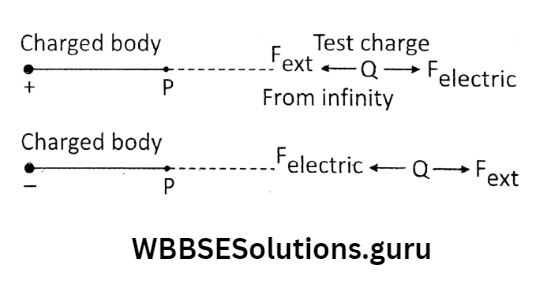
if W amount of work is done in bringing a charge Q.

from infinity to a point P in the vicinity of a positively charged body, then the potential at P is defined as \(v=\frac{W}{Q}.\) [where potential at infinity is assumed to be zero]

This QV amount of work is stored as the electrostatic potential energy within the charge Q.

Both works are done (W) and charge (Q) are scalar quantities so electric potential (V) is also a scalar quantity.

S.l unit of electric potential is volt or V.

From the relation \(\mathrm{V}=\frac{\mathrm{W}}{\mathrm{Q}}, 1 \mathrm{~V}=\frac{1 \mathrm{~J}}{1 \mathrm{C}}=1 \mathrm{~J} / \mathrm{C}\)

What is meant by the electric Potential of a plant being 1 volt?

1 joule of work is done by an external agency in bringing 1 coulomb of charge from infinity to that point.

Potential difference or Voltage: The potential difference (p.d.) between two points is defined as the amount of work done by an external agency in moving a unit positive charge from one point to the other point, without any charge of its K.E.

If W joule of work is done in moving a test charge Q. from point A to point B, then the p.d. between the points is, \(V_B-V_A=\frac{W}{Q}\)

The S.l. unit of potential difference (p.d.) between any two points is a volt.

From the relation,\(\text { p.d. }=\frac{\text { work done }}{\text { charge moved }}\) we obtain, 1 volt = \(=\frac{1 \text { joule }}{1 \text { coulomb }}\)

Thus, if 1 joule of work is done by an external agency in moving 1 coulomb of charge between two points in an electric field, the p.d. between these two points is 1 volt.

Wbbse Class 10 Physical Science Notes

The bigger units of p.d. are kilovolts (KV) and Megavolts (MV). 1KV = 10³V and 1MV = 10⁶V.

We are familiar with the term P.E. or potential at a height. For the motion of the ball, a slope or p.d. is required. Similarly, for the flow of charge, a p.d. or voltage is needed.

When two charged conductors are either placed in contact or connected by a metallic wire, free electrons flow from the conductor with a higher concentration of electrons (at lower potential) to the conductor with a lower concentration of electrons (at higher potential) till both the conductors have an equal concentration of electrons.

In fact, this gives rise to electric current flow in the opposite direction of electron flow. If there is no p.d. there will be no current.

This is similar to the flow of heat in two bodies, and the flow of water in two vessels Flow of heat is due to the difference in temperature,

The flow of water is due to the difference in the level of water or hydrostatic pressure.

WBBSE Chapter 6 Current Electricity EMF And Electrical Cell As Sources Of EMF

We know that for the flow of electric charges through a conductor, a p.d. across its two ends is always needed.

A force is required to set a body in motion. In a similar manner, we can think of a force associated with the motion of charges through an electrical circuit.

Now the question arises -who is pushing/driving the electric charges? This requires a non-electrostatic agency, (like a cell/collection of cells called battery/mains/generator) which is called a source of emf.

Such a source of EMF simply converts some other form of energy into electrical energy.

A cell (or any other electrostatic agency) does not produce charge but maintains a p.d. across its two terminals.

Simply cell is a source of p.d. The word ‘force’ in emf is not used to mean mechanical force (which is measured in Newton) but emf is a potential or energy per unit charge (measured in volts).

That’s why emf can be defined in terms of work done per unit charge.

Definition: Electromotive force (emf) is defined as the amount of work done in establishing the flow of unit positive charge in a closed circuit.

⇒ \(\text { emf }(\varepsilon)=\frac{\text { Work done }}{\text { charge }}\)

Unit of emf \(=\frac{\text { Unit of work done }}{\text { Unit of charge }}=\frac{\mathrm{J}}{\mathrm{C}}=\mathrm{J} / \mathrm{C}=\mathrm{V}\)

This means that the s.l. unit of emf And P.d. is the same volt.

What does the statement ‘The emf of a cell is 1.5 Volt’ mean?

The emf of the cell = 1.5 volt \(=\frac{1.5 \text { joule }}{1 \text { coulomb }}\)

That is, 1-5 joule work is done in moving a charge of 1 coulomb from the positive electrode to the negative electrode of the cell.

WBBSE Chapter 6 Current Electricity Electric Current

The flow of charges (mainly electrons; because electrons are lighter than protons; also protons are tightly bound with the nucleus) from a body at lower potential (- ve potential) to a body at higher potential (+ ve potential) gives rise to an electric current.

Conventional current flows in the opposite direction of the flow of electrons. In the discussion of current electricity, there is a continuous motion of electrons in the wire.

Electric current is defined as the rate of flow of electric charges through a certain cross-section of conductors.

If Q charge flows through a conductor in time t, then the current is, \(I=\frac{\mathbf{Q}}{\boldsymbol{t}}\)

The S.l. unit of current is coulomb/sec and called ampere (A).

The path along which electric current flows is called an electric circuit.

One ampere is the current that flows through a conductor when one coulomb of charge passes through it in one second.

If n electrons flow through the conductor in time t, then Q = n x e, and the current would be \(1=\frac{n e}{t}\) where e = charge on an electron = \(=-1.6 \times 10^{-19} \mathrm{C}\)

∴1C charge is carried by \(\frac{1}{1.6 \times 10^{-19}}\)  electrons\(=6.25 \times 10^{18}\) electrons.

By the statement “1A current flows through a conductor” we mean that 6.25 × 10¹⁸ electrons flow in 1 second across the conductor.

To express weak current, smaller units of current are used. The smaller units are milli-ampere (mA) and micro-ampere (μA).

They are related to ampere (A) as: \(1 \mathrm{~mA}=10^{-3} \mathrm{~A} \text { and } 1 \mu \mathrm{A}=10^{-6} \mathrm{~A} \text {. }\)

Although electric current flows in a particular direction, it is not a vector quantity-as current and does not obey vector addition rules. It adds up like a scalar quantity.

Wbbse Class 10 Physical Science Solutions

WBBSE Chapter 6 Current Electricity Simple Numerical Problems

Question 1. If 6 coulomb of charge flows through a conductor in 3 seconds, find the strength of the electric current.
Answer: Given: 

Charge (Q) = 6C, time (t) = 3s

Current (I) = \((I)=\frac{\mathrm{Q}}{t}=\frac{6 \mathrm{C}}{3 \mathrm{~s}}=2 \mathrm{~A}\)

Question 2. During how much time, a charge of 20 coulomb flows through a conductor to constitute a current of 4 amperes? 
Answer: Given:

Charge (Q) = 20C, current (I) = 4A

Since Current (I) =\((\mathrm{I})=\frac{\mathrm{Q}}{t} \quad \quad t=\frac{\mathrm{Q}}{\mathrm{I}} \quad \text { or, } \quad t=\frac{20 \mathrm{C}}{4 \mathrm{~A}}=5 \mathrm{~s}\)

Question 3. An electric current of 12 ampere flows through a conductor for 15 seconds. Find the amount of charge that flows.
Answer: Given:

Current (I) = 12A, time (t) = 15s Q

As \(\mathrm{I}=\frac{\mathrm{Q}}{t} \text {, so } \mathrm{Q}=1 \times t \text { or, } \mathrm{Q}=12 \mathrm{~A} \times 15 \mathrm{~s}=1800\)

WBBSE Chapter 6 Current Electricity Ohm’s Law Ohm’s Law Concept Of Resistance

Ohm’s law deals with the relationship between voltage (p.d.) and current in an ideal conductor.

Statement: At a constant temperature, the current flowing through a conductor is directly proportional to the potential difference across the ends of the conductor.

Remember that, Ohm’s law is not a fundamental law like Newton’s laws of motion

It is a statement of how voltage and current flowing in a circuit are related to each other, only when the temperature remains constant.

let a current I flow through a conductor when the p.d. across its ends is V, then according to Ohm’s law, \(I \propto V.\) If the current is doubled or tripled voltage will be doubled or tripled.

Similarly, if, the voltage is halved, the current will also be halved. So the reverse relation is also true. Reversing this relation we can get,

⇒ \(V \propto 1\) Or, V = K.l (K= a Proportionality constant) or, \(\frac{V}{\mathrm{l}}=\text { constant }=k\)

If V remains the same then I can increase only if the value of k decreases; the reverse is also true; so that the constant k quantitatively refers to the factor that opposes current.

It is named the resistance of the conductor and it is represented as R.

Thus the Mathematical expression of Ohm’s Law is V=IR

Resistance from Ohm’s law: According to Ohm’s law: V = IR or, R\(=\frac{v}{\mathrm{l}}.\)

That is, at a constant temperature, the ratio of the p.d. across two ends of a conductor.

The unit of resistance is Ohm (Symbol Ω).

⇒ \(1 \text { ohm }=\frac{1 \text { volt }}{1 \text { ampere }}\)

The resistance of a conductor is said to be 1 ohm if 1-ampere current flows through it when a p.d. of 1 volt is applied across its two ends.

The bigger units of resistance are  Kilo-ohm (KΩ²) and Mega-ohm (MΩ)

1KΩ² = 10³ Ω² and 1MΩ² = 10⁶ Ω²

Graphical representation of Ohm’s law: If a graph is plotted taking p.d. V along the x-axis and current I along the y-axis, we will get  \(I \propto V \Rightarrow I=\frac{V}{R}\)

The relation is similar to the equation y = mx. So, the l-V graph is a straight line (OA) passing through the origin and its slope is \(=\frac{y-\text { value }}{x-\text { value }}=\frac{1}{R} \text { : }\)

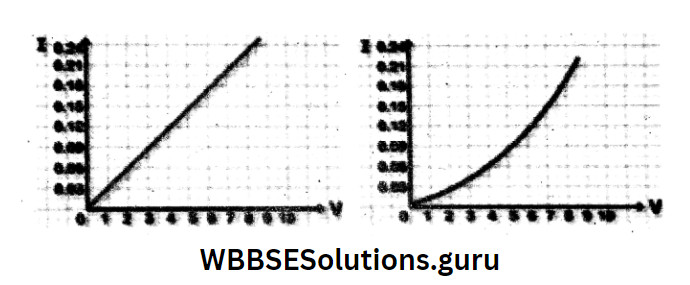
Ohmic conductors: The conductors that obey Ohm’s law are called ohmic conductors, for which the l-V graph is a straight line passing through the origin and the slope of the graph is the same for all values of V and I, that is R is the same, at a given temperature.

Examples: metallic wires.

Non-ohmic conductors: The conductors that do not obey Ohm’s law are called non-ohmic conductors, for which the l-V graph is not a straight line, but a curve, and the ratio V/l is not the same for all values of V and I, that is, R is variable.

Examples: Semiconductors.

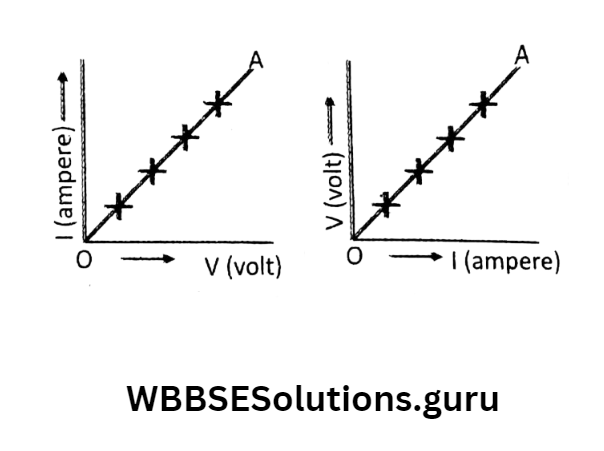
Do all conductors follow Ohm’s law? the p.d. vs current graph for two different conductors A and B. Can you say which conductor has greater resistance?

According to Ohm’s law:  \(V=I R \Rightarrow R=\frac{V}{i}\)

Here, (Slope of A) > (Slope of B) because slope =\(\frac{y-\text { value }}{x-\text { value }}\)

So, A has greater resistance.

WBBSE Chapter 6 Current Electricity Simple Numerical Problems

Question 1. Find the resistance of a wire if 10mA current flows through it and the p.d. across its ends is 2V.
Answer: Given:

Wbbse Class 10 Physical Science Solutions

Current (1) = 10mA = 10×10^-3A, P.d (V) =2V

∴ The Value  Of resistance, R = V/1 = \(=\frac{2 \mathrm{~V}}{10 \times 10^{-3} \mathrm{~A}}=200 \mathrm{ohm}\)

Question 2. Two wires have the same terminal p.d. If the ratio of current flowing through them is 1 : 3, calculate the ratio of their Resistances.
Answer:  By Ohm’s Law: \(I=\frac{V}{R}\)

For the first wire:  \(\mathrm{I}_1=\frac{V}{R_1}\) and for the time second wire: \(\mathrm{I}_2=\frac{V}{R_2}\)

Given:  \(\frac{\mathrm{I}_1}{\mathrm{I}_2}=\frac{1}{3} \quad \frac{\mathrm{I}_1}{\mathrm{I}_2}=\frac{\mathrm{V}}{\mathrm{R}_1} \times \frac{\mathrm{R}_2}{\mathrm{~V}}=\frac{\mathrm{R}_2}{\mathrm{R}_1}\)

⇒ \(\frac{1}{3}=\frac{R_2}{R_1} \Rightarrow \frac{R_1}{R_2}=\frac{3}{1}\)

⇒ \(\text { i.e. } R_1: R_2=3: 1\)

Question 3. 20V of p.d. across a conductor maintains a current of 0-2A. How much p.d. will be required to maintain a current of 250 mA in the same conductor?
Answer: Given: 

V=20V, I=0.2A, R=?

By ohm’s law: \(\mathrm{R}=\frac{\mathrm{V}}{\mathrm{I}}=\frac{20 \mathrm{~V}}{0 \cdot 2 \mathrm{~A}}=100 \Omega\)

if I= 250 mA =250×10^-3A, R=100Ω, then V=?

∴ The required p.d Across the conductor is v=1R=(250×10¯³ A)×(100Ω)=25V

WBBSE Chapter 6 Current Electricity EMF and Internal Resistance of a Cell

EMF of a cell is the potential difference between two terminals of the cell when no current flows i.e. the cell is in an open circuit.

At the time of buying a dry cell from the market, we get the emf value of the cell. But when the cell is connected to an external circuit, it gives a potential difference of less than the EMF value.

Why? Due to internal resistance of the cell (the obstruction offered to current due to electrolytes which act as non-electrical agency).

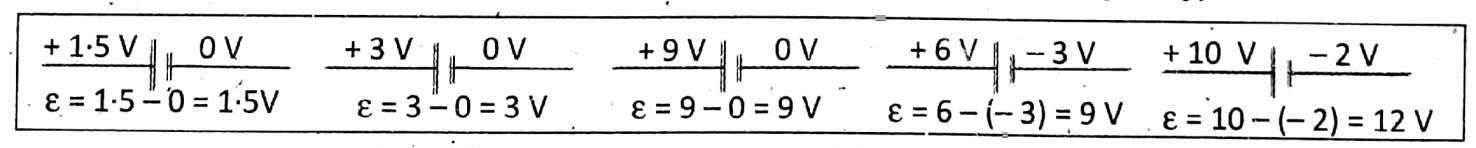
Suppose a cell of emf 8 is connected to an external resistance R and a current I is drawn from the cell.

Under such conditions, the electrolyte inside the cell offers a resistance to the flow of current, known as the internal resistance of the cell denoted as r.

The connecting wires are considered to have no resistance, so in the circuit, there are two resistances external resistance (R) and internal resistance of the cell (r).

∴ Total Resistance of the circuit  =R+r

∴ Current Drawn From the cell \(I=\frac{\text { e.m.f. of the cell }}{\text { Total resistance }}=\frac{\varepsilon}{R+r}\) Or, ε=V+Ir Or, V=ε-Ir Or, ε=I (R+r) IR+Ir

Here the term ‘IR’ is called terminal voltage (V) or potential difference in the external circuit.

So, the terminal voltage is the potential difference across two terminals of a cell when current is drawn from the cell.

The term ‘Ir’ is the voltage drop inside the cell, called the ‘internal potential drop’ or ‘lost volt’. Because this Ir portion of £ is lost due to the obstruction offered by r.

So we can write: emf of a cell = terminal voltage of the cell + lost volt.

In an open circuit (when no current flows in the circuit): I = 0; Ir = 0; ε = V. That is, the emf of a cell in an open circuit = terminal voltage of the cell.

If R = 0 then V = 0  ε= Ir.

That is, m.f. is just the work done inside a cell by the non-electrical agency, in moving a unit positive charge from the negative terminal to the positive terminal of the cell when there is no external circuit.

WBBSE Chapter 6 Current Electricity Resistivity And Conductivity

We have learned about the resistance of a conductor. Here we will discuss other characteristic properties of conductors.

The factors affecting the resistance of a conductor are—

1. nature of the material,
2. length,
3. area of cross-section and
4. temperature.

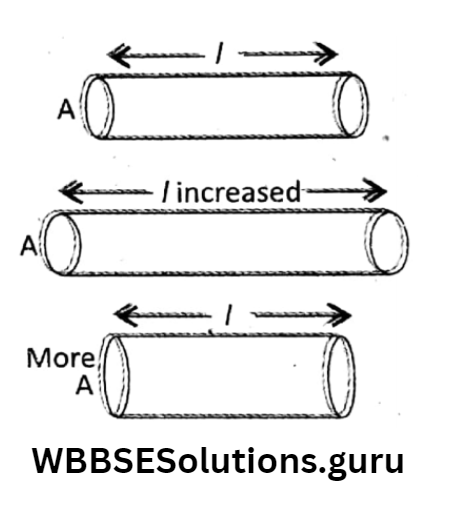
Dependence on length and area of cross-section I (Temperature and nature of material remain same): Suppose we have a conductor of length l and cross-sectional area A.

Its original resistance is R.  1. If l is made to keep the same A, then resistance will also increase.

Thus, resistance is direct R\(\propto\)I (when A remains unchanged).

This means the more the length, the more the resistance, 2. If A is made to increase while keeping the same /, then resistance will decrease. Thus resistance is inversely proportional to area.

Mathematically, \(R \propto \frac{1}{A}\) (when I remain unchanged) is proportional to length. Mathematically, R remains unchanged).

This means, the larger the area, the smaller the resistance. Combining these two or specific we get, \(R \propto \frac{1}{A} \Rightarrow R=\rho \cdot \frac{1}{A} \Rightarrow \rho=\frac{R A}{I}\) resistance of the material of the wire.

In the reaction R=ρI/A, If I=1 and A=1 Then R=ρ. Thus, resistivity is the resistance of a conductor of unit length and unit area of the cross-section at a constant temperature.

Both resistance and resistivity are resistances. Then, what is their difference? Resistance will change with the change of / and A.

But when / and A have unit values, then the resistance is resistivity. If we change the material, we find different p.

So, resistivity is a characteristic property of a material. Resistivity depends on the nature of the material and the temperature of the conductor but not upon the dimensions (/, A).

S. I Unit of Resistivity: From the relation R= ρ I/A, We have ρ=RA/I

∴ Unit of ρ =  \(\frac{\text { Unit of } R \times \text { Unit of } A}{\text { Unit of } I}=\frac{\text { ohm } \times \mathrm{m}^2}{\mathrm{~m}}\)

The Statement ‘Resistivity of copper = 1.62×10¯⁶  ohm. cm’ means that a Conductor made of copper having a length, equal to

The statement ‘resistivity of copper = 1.62 x 10^-6 ohm. cm’ means that a conductor made of copper having a length, equal to 1 cm and an area of 1 cm² has a resistance of 1.62 x 10^-6 ohm between its two opposite faces at a particular temperature.

If a wire is stretched to double its length, what will be the change in R and p ? Since the material of the wire remains unchanged, so p will not change. But as R\(\propto\) so R will be doubled.

What would happen to the resistance of a wire if its radius or diameter is 1. doubled and 2. halved?

If r = radius and d = diameter of a write then its area of cross-section is \(A=\pi r^2=\pi\left(\frac{d}{2}\right)^2=\frac{\pi d^2}{4}\).

Resistance of wire \(R=\frac{\rho /}{\pi r^2}=\frac{4 \rho /}{\pi d^2}\)

That is, \(\mathrm{R} \propto 1 / r^2 \text { and } \mathrm{R} \propto 1 / d^2\) (when ρ  and I are fixed)

So, if the radius or diameter of a wire is doubled, its Resistance lessens to 1/4th of its initial value.

If the radius, or diameter of a wire is doubled, its resistance increases to 4 times its initial value.

If a wire is stretched to 3 times its length. Will there be any change in resistivity and resistance? Here resistivity (p) will not change, since the material of the wire remains unchanged.

Here, resistivity (ρ) will not change, since the material of the wire remains unchanged. here,

⇒ \(R_1=\frac{\rho l}{A} \text { and } R_2=\frac{\rho 3 l}{A / 3}=9 \cdot \frac{\rho l}{A}=9 \cdot R_1 \Rightarrow \frac{R_2}{R_1}=9 \Rightarrow R_2=9 R_1 \text {. }\)

Hence, resistance will be 9 times its initial value.

The resistance of a metallic wire increases with an increase in temperature. This is so why a “fixed temperature” is mentioned in defining resistivity.

Electrical conductivity: Just like resistance in a conductor there is another factor known as conductance (G).

Reciprocal resistance is called \(\left(\frac{1}{R}\right)\)conductivitance. The \(\sigma=\frac{1}{\rho}=\frac{1}{\mathrm{RA}}\)reciprocal of resistivity is called the electrical conductivity.

It is represented as a property of the conductor whereas ρ is a property of the non-conductor/ insulator. A good Conductor should have a high value of σ and a low value of ρ.

Units of electrical conductivity: In S.l. the system, ohm^-1.m^-1 or mho.m^-1 or S.m^-1, and CGS system, ohm^-1.cm^-1 or mho.cm^-1.

Conductors and Insulators: Substances with low resistivity and high electrical conductivity are good conductors. They allow an electric current to flow easily.

Most metals (Ag, Cu, Al ….) are good conductors. On the other hand, insulators have very high resistivity and their electrical conductivity is very low (almost nil).

Examples— are wood, rubber, plastic, etc. Insulators are mainly used to protect us from electrical shock because of their poor electrical conductivity.

Resistivity is a more fundamental property as compared to resistance. Because the resistance of wire changes with the change of its length and area of cross-section; the resistivity remains unchanged for such changes.

Resistivity depends on oh temperature,

For metals, resistivity increases with the increase in temperature, and For semiconductors, it decreases with the increase in temperature.

For alloys, it remains nearly unaffected by the change in temperature. For example, the resistivity of constant (Cu + Ni), and manganin (Cu + Mn + Ni) remains almost constant with the rise in temperature.

Represents the resistivity of some substances. The values of resistivity help us to recognize conductors, semiconductors, and insulators separately.

Resistivity depends on the material of the substance, For metals, it is very low (-10^-8Ω.m), for semiconductors, it is low (-10^-5Ω.m) and for insulators, it is very high (-10^-13Ω.m).

For electrical connections and power transmission, the wires used should possess negligible resistance and very small resistivity.

Copper or aluminum possesses such qualities. This is the fact why the wires are generally made of copper or aluminum.

Generally, the standard resistors are made from alloys, such as manganin, constant, nichrome, etc. These are so chosen as their resistivity remains practically constant with the change in temperature.

The filament of a bulb is made by using tungsten. Because it has-

1. High melting point and
2. High resistivity.

The resistance of the tungsten filament of a bulb is more when it is glowing as compared to when it is not glowing.

This is so because in the glowing condition, the filament is at a high temperature, and for it, the resistance increases.

The resistivity of an alloy is more than that of its constituent metal. For example, the resistivity of the constant (Cu + Ni) is nearly 30 times more than that of Cu.

The heating element of the heater is made by using a nichrome (Ni + Cr + Fe) wire because of its high resistivity.

A fuse wire is made from an alloy of lead and tin in a ratio: of 1. Because it has a low melting point and high resistivity.

Superconductor: Generally, the resistivity of metals decreases with the decrease in temperature.

There is a category of substance whose resistivity becomes almost zero at a lower temperature less than a particular value, called critical temperature and this type of substance is called superconductor.

For example, mercury below 4-2K behaves as a superconductor. Superconductors have infinite conductivity.

Resistivity-temperature graph: the resistivity-temperature graph.

The utility of the graph is to identify the metallic conductors, semiconductors, and superconductors on the basis of the variations of their resistivity with different temperatures.

WBBSE Chapter 6 Current Electricity Series And Parallel Combination Of Resistances

Sometimes two or more resistances are connected together to make a combination of resistances for different purposes in electric circuits.

There are two ways of a combination of resistances—

1. series combination and
2. parallel combination.

Series combination:

Two resistances R₁ and R₂ are connected in series (end-to-end). In this combination, let us look at the p.d. across each resistance and the current flowing through them.

Since the resistances are connected end-to-end, the same current (suppose I, the main current) flows through each resistance.

If V is the supplied p.d. of the battery then V is divided into two parts V₁ and V₂ across R₁ and R₂ respectively V= V₁ + V₂.

According to Ohm’s law: V1 = \(l_1=\frac{V}{R_1}\) and V₂ = \(l_2=\frac{V}{R_2}.\)

If R_s be the equivalent resistance of this series circuit, then V = \(l_s=\frac{V}{R_s}\)

Since l = l₁ + l₂

∴ \(\frac{V}{R_p}=\frac{V}{R_1}+\frac{V}{R_2} \Rightarrow \frac{1}{R_p}=\frac{1}{R_1}+\frac{1}{R_2}\)

If three resistances R₁,R₂ And R₂ are connected in series then \(\frac{1}{R_p}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}\)

In a series combination, the equivalent resistance is more than the highest value of the resistance connected.

But in a parallel combination, the equivalent resistance is less than even the smallest resistance connected.

That is R_s >R₁ R₂, R₃, … and R_p <R₁ R₂,R₃,…….

In series combination, p.d. gets divided but the same current flows through each resistance. In

parallel combination, p.d. remains the same across the resistances but the current gets divided.

When the resistance of the combination is to be increased, the series combination is preferred, and when the resistance is to be reduced,

i.e., if more current is to pass through the circuit, the parallel combination is preferred.

WBBSE Chapter 6 Current Electricity Simple Numerical Problems

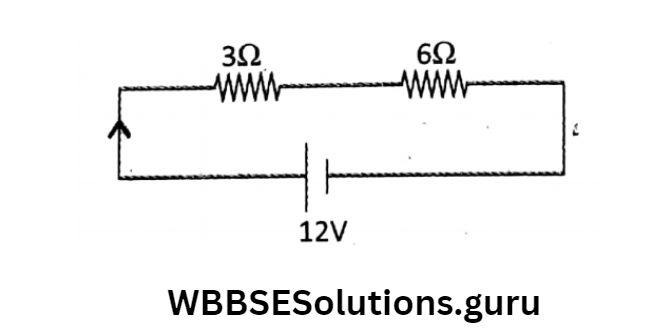
Question 1. Two resistances 3Ω and 6Ω are connected in (1) series and (2) parallel with a supply voltage of 12V. Draw the circuit diagrams. Then find a current and potential drops in all resistances.
Answer: (1) Series Combination 

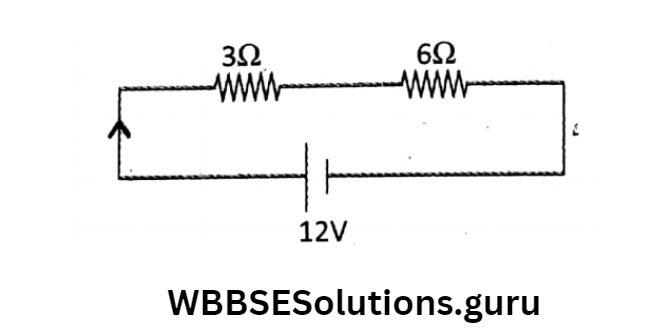
Here Equivalent resistance,

R_e = R₁ + R₂= 3+6= 9Ω

Current Flows Through each resistance,

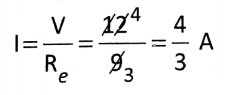
The potential drop in 3Ω,

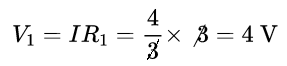
The potential drop in 6Ω,

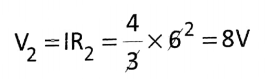
Wbbse Class 10 Physical Science Solutions

(2) Parallel Combination 

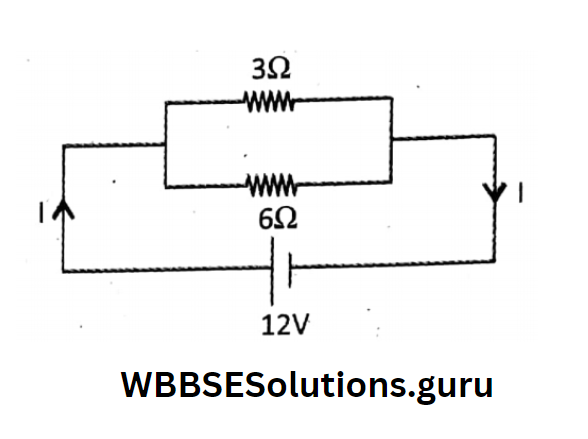
⇒ \(\frac{1}{R_e}=\frac{1}{R_1}+\frac{1}{R_2}=\frac{1}{3}+\frac{1}{6}=\frac{2+1}{6}=\frac{3}{6}=\frac{1}{2}\)

R_e=2Ω

Main Current, \(\mathrm{I}=\frac{\mathrm{V}}{\mathrm{R}_e}=\frac{12}{2}=6 \mathrm{~A}\)

⇒ \(l_1=\frac{V}{R_1}=\frac{12}{3}=4 \mathrm{~A} \text { and } I_2=\frac{V}{R_2}=\frac{12}{6}=2 \mathrm{~A}\)

Potential Drop across 3Ω and 6Ω resistance is the same = 12 V.

Wbbse Class 10 Physical Science Solutions

Question 2. What will be the equivalent resistance of the combination of resistors 1Ω, 10Ω, and 100Ω (1) in series combination and (2) in parallel combination?

(1) The equivalent resistance in a series combination

R_s = 1Ω+10Ω+100Ω=111Ω

(2) The equivalent resistance in parallel combination

⇒ \(\frac{1}{\mathrm{R}_p}=\frac{1}{1}+\frac{1}{10}+\frac{1}{100}=\frac{100+10+1}{100}=\frac{111}{100}=0 \cdot 9 \Omega\)

Activity: We make two circuits Two identical bulbs are connected (1) in series (end-to-end) and (2) in parallel combination (between two common points).

We are to compare how the brightness of each bulb varies in the two combinations. Here the bulbs act as resistors since the resistance of the connecting wire is neglected.

In a series combination, the same current flows through each bulb, while the equivalent resistance becomes more than either of the two resistances.

So, the electric current becomes less, and as a result of which, bulbs glow dimly, and the brightness of each bulb diminishes.

In parallel combination, each of the two bulbs is connected across the two ends of a cell. The equivalent resistance of this combination becomes lower than either of the three resistances.

So, the electric current becomes more. The current in each bulb remains unaffected by the presence of another bulb.

So, the bulbs glow as bright as they were connected individually to the supply voltage.

Due to this fact, in your house bulbs/fans/TV/computer, etc. all are connected in parallel combination with the supply voltage.

WBBSE Chapter 6 Current Electricity Heating Effect Of Electric Current Joule’s Law of Heating Effect Of Current Concept Of Electrical Energy

When an electric current flows through a conductor in any direction, it gets heated up and this fact is known as the heating effect of current.

Why this heating effect is happening?  Whenever a conductor is connected to a voltage source, the electrons present in the conductor start moving towards the higher potential (+ ve terminal of the battery).

During this movement, electrons collide with atoms, ions, etc. present in the conductor.

As a result of which, electrons have to overcome the resistance of the conductor, and a loss of energy of electrons takes place.

This energy gets converted into heat energy for which the heating of the conductor takes place.

The heating effect of current plays an important role in home appliances like electric kettles, electric stoves, electric irons, electric cookers, etc.

Whenever you keep your mobile connected to a charger for a long time or when you watch TV for a long time while touching your mobile/TV you feel hot; even a fan or every electronic gadget gets hot.

Mathematics: Suppose a p.d. V is applied across a conductor. Here, the cell is not producing charge it only gives energy to electric charge.

Thus, the cell does some electrical work.

⇒ \(\mathrm{V}-0=\frac{\mathrm{W}_{\text {ext.agency }}}{\mathrm{Q}}=\frac{\mathrm{W}_{\text {done by cell }}}{\mathrm{Q}} \Rightarrow \mathrm{W}_{\text {done by cell }}=\mathrm{E}_{\text {supplied by cell }}=\mathrm{VQ} \ldots \ldots . \text { (i) }\)

Suppose the cell allows I current to flow through a resistance R  of the Conductor for time t. Then the amount of charge flown in time t will be \(1=\frac{Q}{t} \quad Q=I t\)

Using the value of ‘Q’ From (2) Into (1):  W=V×I×t……….(3)

According to Ohm’s Law: V= IR. So that W= IR×I×t⇒ W= I²Rt…………(4)

Again using Ohm’s Law: \(I=\frac{V}{R}.\) Then \(\mathrm{W}=\frac{\mathrm{V}^2}{\mathrm{R}^2} \times \mathrm{R} \times t \Rightarrow \mathrm{W}=\frac{\mathrm{V}^2}{\mathrm{R}} t\)…………………(5)

This work appears as the heat energy in the conductor.

From the work-heat equivalence of heat\(W=J H \Rightarrow H=\frac{W}{J}\) (as stated in class IX), relations (3), (4).and (5) can be expressed in terms of heat produced.

We know that J = 1 in the SI system and J = 4-2 joule/cal in the CGS system. So the relations for heat produced in a conductor are

H= \(\mathrm{VIt}(\mathrm{SI}) \text { and } \mathrm{H}=\frac{\mathrm{VIt}}{4 \cdot 2} \mathrm{cal}(\mathrm{CGS})\)

H = \(\mathrm{I}^2 \mathrm{R} t(\mathrm{SI}) \text { and } \cdot \mathrm{H}=\frac{\mathrm{I}^2 \mathrm{R} t}{4 \cdot 2} \mathrm{cal}(\mathrm{CGS})\)

H= \(\frac{\mathrm{V}^2}{\mathrm{R}} t(\mathrm{SI}) \text { and } \mathrm{H}=\frac{1}{4 \cdot 2} \cdot \frac{\mathrm{V}^2}{\mathrm{R}} t \mathrm{cal} \text { (CGS) }\)

These relations are known as Joule’s law of the heating effect of the current

According to this equation:

⇒ \(H \propto R\)(R, t constant),

⇒ \(H \propto R\)(I, t constant) and

⇒ \(H \propto t\)(I, R constant)

Joule’s laws of heating effect of current: There are three laws.

First Law: The amount of heat H produced in a conductor is directly proportional to the square of the current (I) flowing through it when resistance and time of flow of current remain the same, i.e. \(\mathbf{H} \propto \mathbf{I}^2\) (When R and t remain constant)

Second Law: The amount of heat H produced in the conductor is directly proportional to the resistance R of the conductor when the current and time of flow of current remain the same, i.e.,  \(H \propto R\)(When I and t remain constant),

Third Law: The amount of heat H produced in the conductor is directly proportional to the time of flow t of current when current and resistance remain the same, i.e., \(H \propto R\) (When I and R remain constant)

WBBSE Chapter 6 Current Electricity Domestic Uses Of Heating Effect Of Current

The common household electrical appliances which make use of the heating effect of current are electric heaters, irons, bulbs, geysers, toasters, ovens, immersion heaters, etc.

Electric heater: The heating coil in an electric heater is made of nichrome (an alloy of 60% Nickel, 25% iron, and 15% chromium) wire (it is also called a heating element).

1. Because nichrome
2. Has a high resistivity,
3. A high melting point, and

Does not get oxidized up to a temperature of about 1000°C. The nichrome wire is wound in the form of a helical coil and placed in some insulating material (it protects the user from electric shock).

When an electric current passes through the coil, it becomes very hot.

Electric iron: Electric iron is used for pressing clothes. The heating element in iron is a flat nichrome coil wound on a mica sheet.

The coil is made flat so that the heat spreads over a large surface area. When an electric current passes through the heating element, it produces heat energy.

Electric bulb An incandescent electric bulb consists of a very fine coil of tungsten. Tungsten has a Very high resistivity,

Wbbse Class 10 Physical Science Notes

The very high melting point of about 3300°C. The bulb is filled with argon gas at very low pressure and completely evacuated.

When an electric current is passed through this, the filament gets heated up and it emits heat energy and light energy. This is due to the heating effect of the current.

Fuse or cut-out: The fuse is a safety device in an electric circuit. It protects electric circuits and electrical appliances by stopping the flow of electric current.

Wbbse Class 10 Physical Science Notes

The material of the fuse wire is made from an alloy of lead and tin in a ratio 3: of 1. It has

1. A low melting point and
2. A high value of resistance.

When the circuit becomes overloaded due to short-circuiting or fluctuation of current /the fuse melts and breaks the circuit and thus the electrical appliances are saved.

When the live wire and the neutral wire come in direct contact, it is called a short circuit.

Wbbse Class 10 Physical Science Notes

The fuse is always connected to the live wire in an electric circuit, at the point where current enters the circuit.

If the fuse is connected to the neutral wire, it will melt when there is overloading. Under such conditions, if an electrical appliance is touched, even in the OFF position, the person will get a shock as the appliance is connected to the live wire.

Wbbse Class 10 Physical Science Notes

To protect electric appliances like T. V. sets, Refrigerators, geysers, Iron, mixers, etc. cartridge fuses are used. These are fixed within the appliance.

Such fuses have a maximum tolerance current.

To protect a circuit, the fuse should be of a lower value of current than the maximum current that the circuit can withstand. Fuse ratings (e.g. 5A, 10A, 15A, ) ensure it.

For example, a 5A fuse can withstand a maximum of 5A current. If a current of more than 5A flows, the fuse melts.

These days, the use of MCB or Miniature Circuit Breaker Mechanical Circuit Breaker is very popular rather than traditional fuses.

It is used to protect each individual circuit; If the circuit is overloaded, the MCB falls down to switch off the circuit without causing damage.

Wbbse Class 10 Physical Science Notes

WBBSE Chapter 6 Current Electricity Electrical Power

In Physics, power is defined as the rate of doing work. So, Electrical power is defined as the rate of doing electrical work or the amount of electrical work done in 1 second. Mathematically

Wbbse Class 10 Physical Science Notes

P\(\frac{\text { Electric work done or energy supplied by the cell }}{\text { time }}=\frac{W}{t} \text { or, } \frac{E}{t}\)

But, \(\text { But, } W=V I t \quad P=\frac{V I t}{t}=V I \quad P=\frac{I^2 R t}{t}=I^2 R\)

P=\(\frac{V^2}{R^2} \times R=\frac{V^2}{R} \text { for fixed } V \text {. }\)

Any relation can be used to calculate electrical power.

Remember: Electrical power is supplied by a cell or any other voltage source and power is always dissipated in a resistor, across which the source is connected.

The S.I. unit of electrical power is the watt (or W). Bigger units of power are kilowatts (KW), and megawatt MW where 1 kW = 10³ W and 1 MW = 10⁶W.

Electrical power is said to be 1 watt when 1 joule of electrical work is done in 1 second, Or, the cell supplies 1 joule of energy in 1 second to the electric charge.

Units of electrical energy: An electrical bill is prepared on the basis of the amount of electrical energy (E) consumed in our homes/schools/industries.

The basic formula is E = P x t i.e. electrical energy consumed = electrical power x time. The commercial unit of electrical energy is watt-hour (W-h) and kilowatt-hour (kW-h).

1 watt-hour = 1 watt x 1 hour = 1 watt x 3600s = 3600 joule.

1 kilowatt-hour = 1 kilowatt x l hour = 100 Js^-1 x 3600s = 3-6 x 10⁶ = 3.6 MJ.

B. O. T. (or Board of Trade) unit: The bigger unit of electric energy is a kilowatt-hour. It is also known as B.O.T.

(Board of Trade Unit), which is the electric energy spent by an electric appliance of power 1 kilowatt used for 1 hour.

⇒ \(1 \text { B.O.T. unit }=1 \mathrm{kWh}=\frac{\text { watt } \times \mathrm{h}}{1000}=\frac{\text { volt } \times \text { ampere } \times \mathrm{h}}{1000}\)

WBBSE Chapter 6 Current Electricity Simple Numerical Problems

Question 1. A battery of 12V supplies a 2A current. Calculate its power.
Answer: Given: V = 12V, I = 2A So, power supplied by the battery P = V x l = 12 x 2 = 24 watt = 24 J/s.

Question 2. A torch bulb of 4-5V draws a current of 0-3A. If the bulb is switched on for 10 minutes, find out the energy released by the bulb.
Answer: Given: V – 4.5V, I = 0.3A, t = 10 min = 600s

The energy released by the bulb, E = Vlt = 4-5 x 0-3 x 600 = 810J

Question 3. An electric bulb of resistance of 500Q draws a current of 0.4A. Calculate its power.
Answer: Given: R = 5000, I = 0.4A, P = ?

Electric power P = l²R = (0-4)²x 500 = 80 watt

Wbbse Class 10 Physical Science Solutions

Question 4. A family uses one 100W bulb, one 100W fan, and one 1000W heater for 8h daily. Calculate the daily household electric bill, if one unit costs Rs. 3-00.?
Answer: The electrical energy consumed per day is

⇒ \(=\frac{\text { watt } \times h}{1000}=\frac{(1 \times 100+1 \times 100+1 \times 1000) \times 8}{1000}=9.6\)

Daily electric bill costs = Rs. 3.00 x 9.6 = Rs. 28.80.

Question 5. Two electric bulbs of 100W and three electric fans of 60W are used daily for 5 hours. What will be the cost for it in one month (30 days)? The cost of each unit is Rs. 3.50.
Answer:  The electrical energy consumed per day is

⇒  \(=\frac{\text { watt } \times h}{1000}=\frac{2 \times 100 \times 5+3 \times 60 \times 5}{1000}=1.9\)

The total electrical energy consumed in 30 days =1.9×30=57

∴ The cost of it is = Rs. 3.50 × 57 = Rs.199.50

If The Bulb is Connected To a p.d. less than 220V (say 110V), the build will consume less power and will glow dimly.

Then power Consumed will be, \(P=\frac{V^2}{R}=\frac{(110)^2}{484}=25 \mathrm{~W}\)

Rating And Its Significance: 

• In general, electrical appliances such as electric bulbs, irons, heaters, geysers, washing machines, etc. are rated by their power and voltage.
• This is known as power-voltage rating or simply power rating. This power rating is done to calculate
• The resistance of the appliance and
• The safe limit of current that can pass through it.

For example, an electric bulb rated as 100W, 220V means that when the bulb is connected to a 220V main line, it glows fully and consumes 100W power or 100J of electrical energy in 1 second.

While glowing the resistance of the filament of the bulb is, \(R=\frac{V^2}{P}=\frac{(220)^2}{100}=484 \Omega\)

The safe limit of current that flows in the Bulb is \(I=\frac{P}{V}=\frac{100}{220}=0.45 \text { (approx) }\)

• Three different types of light bulbs are available in the market. These are Incandescent bulbs, CFL (Compact fluorescent lamps), and LED (Light Emitting Diode).
• CFL and LED are more efficient than incandescent bulbs from the point of the energy economy. Incandescent bulbs contain tungsten filaments.
• When an electric current is passed the filament gets heated up and emits light. More than 95% of the energy gets converted into heat energy.
• Only less than 5% of the energy is converted into light energy. That’s why an incandescent bulb becomes hot when switched on.

A CFL contains argon and a small amount of mercury vapor when a current is passed, this generates UV light and excites the fluorescent coating inside the bulb which produces visible light.

• On the other hand, LEDs are semiconductors.
• When current (i.e. electrons) is passed, they emit light. Out of these three, LED is better than others.
• CFL is not eco-friendly like LED, because CFL contains toxic mercury vapors.

Significance of the energy rating mark given in household electrical appliances: The Bureau of Energy Efficiency (BEE) under Govt, of India, suggests marking the energy star level of household electrical appliances, such that, 5 stars (*) appliances save maximum energy while 1-star (*) appliances save the least energy.

From the point of the energy economy, a buyer should use 5-star appliances to save on electricity bills.

Activity:

(1)Value development against misuse of electrical energy: We are all aware of today’s energy crisis, lack of fossil fuels, load shedding scenario, along needless misuse of electricity at homes, schools, government offices, etc.

The best thing to do for us is to minimize wastage. It requires common people’s awareness. Government-level initiatives are also required.

These days more efficient CFL and LED bulbs are available. Although these are expensive, they are 4-6 times more efficient than filament-based bulbs, They are useful against misuse of electrical energy.

An incandescent bulb of power 100 W has the same brightness as a CFL bulb of power 24 W and an LED bulb of 16 W.

(2) Suppose two bulbs rated as SOW and 100W are connected in series and in parallel with the same voltage line. In the two cases which bulb glows more brightly than the other?

1. In a series of connections between the bulbs, the same current flows through each bulb. That is,

I= Constant. As\(P=V^2 / R, \text { so } P \propto \frac{1}{R}\) for the same V i.e. resistance of 60 W bulb is more than the 100W bulb.

As \(P=1^2 R \text {, so } P \propto R \text {. }\) Hence, the 60W bulb glows more brightly.

2. In parallel connection of the bulbs, the current in each of them does not remain the same (although the p.d. V remains constant).

Remember: Resistance of a Particular build remains the same as \(R=\rho \frac{1}{A}. \text { As } P=\frac{V^2}{R}\) \(P \propto \frac{1}{R} .\) Thus, for the same v, the 100W bulb glows more brightly.

WBBSE Chapter 6 Current Electricity Electromagnetism Action Of Electric Current On Magnet

Magnetism has been known since ancient times and electricity has been discovered in the 1700s. Until 1820, electricity and magnetism were studied as two separate branches.

Electricity was considered a phenomenon related to electric current, while magnetism was considered to be related to magnets.

In 1820, famous physicist Hans Christian Oersted first experimentally proved that a current-carrying wire behaves like a magnet, or a current-carrying wire produces a magnetic field around itself as long as the current is passed through it.

This is known as the magnetic effect of electric current. Oerested proved that electricity and magnetism are related to one another.

Today we have a new branch of study known as electromagnetism.

Activity: Oersted’s experiment: Materials required: A magnetic compass (tiny magnet), Cu wire, battery with crocodile clips, and a few carrom coins.

Procedure: Fix carrom coins on a table with the help of glue tape over which stick the Cu wire. Place the magnetic compass below the Cu wire.

At this position, the magnetic compass needle points in a geographical north-south direction.

Then connect the H-Ve and -Ve terminals of the battery with two ends of Cu wire and allow current to flow.

Observations: The compass needle at once gets deflected to one side deflection towards the East). A magnet can only influence another magnet.

So we can say that a current-carrying wire exerts a force on a magnet.

If the amount of current is increased, then the magnetic compass shows a larger deflection.
So, the magnetic field produced in the wire is directly proportional to the electric current.

Current is passed through the Cu wire and the compass is taken slightly away from the Cu wire. The deflection of the magnetic needle decreases the Greater the distance weaker the magnetic field.

Place the compass above the wire. The magnetic needle deflects in the opposite direction (deflection towards the west).

As if the direction of the electric current is reversed, the direction of deflection of the magnetic needle gets reversed.

So we can say that the direction of the magnetic field can be reversed by reversing the direction of the current flow.

Rules for determining the direction of deflection of magnetic needle: The direction of deflection of the magnetic needle due to current can be determined by any one of the following two rules:

1. Ampere’s swimming rule: If a swimmer stretching his arm is swimming along a current carrying wire in the direction of the current, facing the magnetic needle, then the direction in which the left hand of the swimmer points gives the direction of deflection of the north pole of the magnetic needle

Explanation on the basis of observation of Oerested’s experiment: Suppose the wire is placed over the compass through which current flowing from S→N due to which [following SNOW Rule (S: South, N: North, O: Over and W: West – Where anyone change of S/N/ O/W, deflection of N-pole will be changed to either E or W and for two changes deflection will be a pole of the magnetic compass will be deflected towards West.

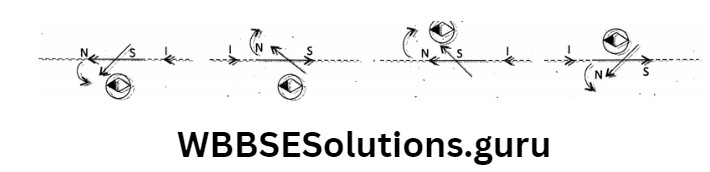
2. Wire is over the compass and current flowing from N→ S for which [following NSOE Rule] N-pole of the magnetic compass will be deflected towards East,

3. Wire is placed below the compass and current flows from S to N for which N-pole will be deflected towards East [following SNBE Ruie.]

4. (following NSBW Rule) N-pole will be deflected towards the West. (As a whole this rule is very complex).

Right-hand grasp rule: If we hold a current-carrying conductor in the right hand such that the thumb points in the direction of flow of current, then the direction in which other fingers curl/wrap gives the direction of the magnetic field.

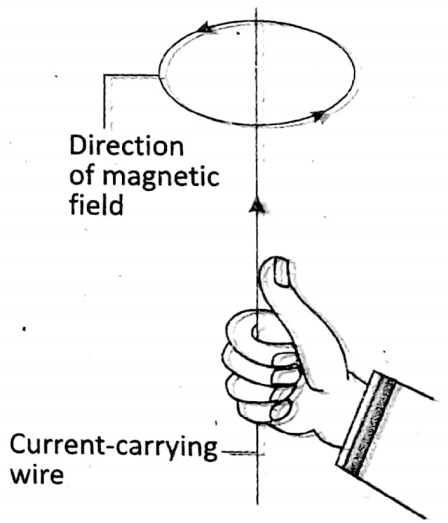
Explanation: According to the right-hand grasp rule, keeping the thumb towards the direction of current, the direction along which other fingers curl for gripping the wire, produces a circular path.

For which the current is flowing in an upward direction and for which the current is flowing in a downward direction.

This circular path gives the direction of the magnetic field produced due to current this is the direction along which a north pole moves. [This rule is easier).

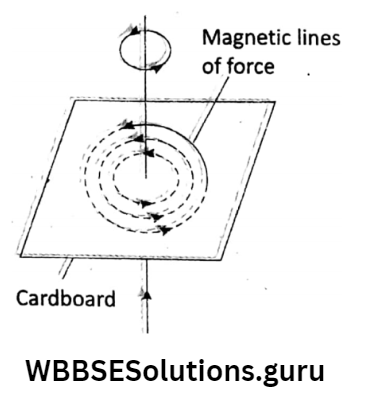
Magnetic field around a long straight wire: A straight wire passes vertically through a hole made at the center of the cardboard. Some iron filings are sprinkled on the cardboard.

A current is passed through the wire in an upward direction and the cardboard is gently tapped. The iron filings get arranged along some concentric circles around the wire.

The arrows show the direction of the magnetic field. It is observed that a straight current-carrying wire produces a magnetic field that looks like concentric circles around the wire.

Here, the magnetic field strength is very weak.

Magnetic field around a circular wire: A straight wire is bent into a circular loop. The loop passes through two points on cardboard.

Some iron filings are sprinkled on the cardboard. A current is passed through the loop and the cardboard is gently tapped.

Shows that the iron filings get arranged along two sets of concentric circles for each end of the wire.

The arrows show the direction of the magnetic field. The magnetic field of a circular loop is stronger than a straight wire.

How? Imagine the loop is divided into small segments which are nearly straight wires. Each straight segment produces a magnetic field in the shape of concentric circles.

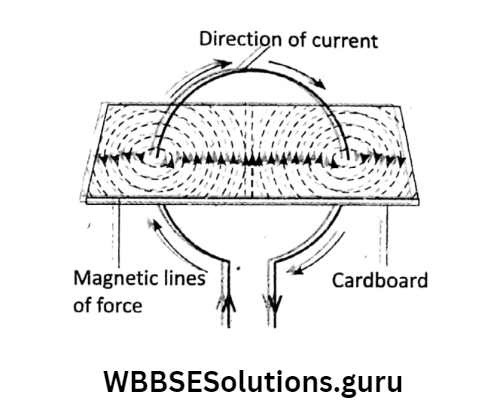
At the center of the loop, the magnetic field lines are almost straight and they add up which the magnetic field becomes stronger.

If instead of one loop, there are N loops then the magnetic field will be N times stronger.

The similarity between a field due to a magnetic pole and a field due to a circular current-carrying loop:

In a circular current-carrying loop, the magnetic field lines at the center, are along the axis of the loop and normal to the plane of the loop.

If the loop is replaced by a thin magnet, similar types of magnetic field lines will be obtained. That is, the behavior of a current-carrying loop is similar to that of a magnetic pole.

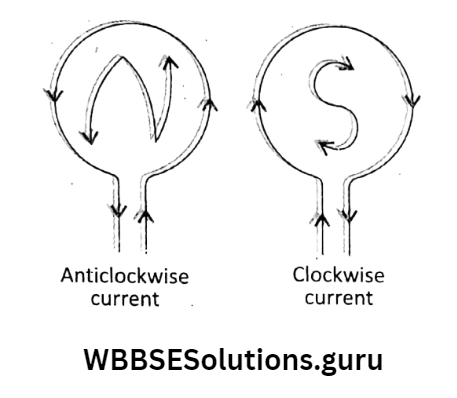
Polarities in a current-carrying loop: If you look at the face of the loop and assume that the current flows in an anticlockwise direction then the face of the loop acts as a north pole and for the flow of current in a clockwise direction, the loop acts as a south pole.

WBBSE Chapter 6 Current Electricity Action Of Magnet On Current

We learned that a current-carrying wire exerts a force on a magnet. Is the reverse also true? Can a magnet exert a force on a current-carrying wire?

In 1821 Michael Faraday experimentally observed that whenever a current-carrying wire is placed in a magnetic field the current-carrying wire experiences a mechanical force acting on it which is known as a magnetic force.

If there is no current in the wire, there is no force. If the wire is free to move, it will produce motion wire.

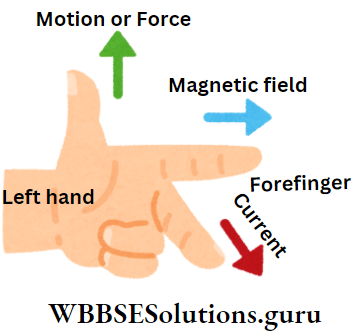
This is known as the action of a magnet on current. The direction of force or motion of the conductor can be found by Fleming’s left-hand rule.

Fleming’s left-hand rule: Stretch the first three fingers of the left hand mutually perpendicular to each other such that if the forefinger indicates the direction of the magnetic field and the middle finger indicates the direction of current, then the thumb will indicate the direction of force or motion of the conductor.

Principle of working of Barlow’s wheel: Whenever an electric conductor is brought in a magnetic field, the conductor gets motion due to the presence of the magnetic field. One such example is Barlow’s wheel.

It is a suitable instrument that shows how motion is produced in a current-carrying conductor placed in a magnetic field. In it, electrical energy is converted into mechanical energy.

The direction of rotation of the wheel can be determined by applying Fleming’s left-hand rule.
Barlow’s wheel consists of a star-shaped copper wheel, capable of rotating freely in a vertical plane about a horizontal axis.

A pool of mercury is kept in a small groove on the wooden base of the apparatus such that the point of each spoke of the wheel just dips into the pool of mercury while rotating.

The pool of mercury is kept in between the NS poles of a strong magnet When the axis of the wheel and the mercury are connected to a battery, the circuit is completed and the wheel starts rotating due to the action of the magnet on the current.

While rotating, when a spoke of the wheel just leaves mercury, the circuit breaks out, but due to inertia of motion, the next spoke comes in contact with mercury, thereby rotation of the wheel continues.

The speed of rotation of Barlow’s wheel depends upon the—

1. The strength of the magnetic field, and
2. The strength of the current.

The rotation of Barlow’s wheel increases with increasing the current. The wheel rotates in the opposite direction when the current is reversed.

The rotation of Barlow’s wheel is possible in D. C. only, but not in A.C.

Reason: In A. C., the direction of rotation of the wheel changes its direction during each half-cycle. Ultimately, no rotation of the wheel is possible in A.C.

WBBSE Chapter 6 Current Electricity Electric motor

What makes an electric fan move? Electric motor. In many instruments like tulle pumps, toys, washing machines, mixers, grinders, etc.

electric motors are used. An electric motor works due to the action of a magnet on current.

An electric motor is a device that directly converts electrical energy (d.c.) into mechanical energy (specifically rotational kinetic energy).

Working principle of an electric motor: When an electric current is passed through a rectangular coil placed in a magnetic field, two equal and opposite forces act on two arms of the coil, as a result of which the coil begins to rotate continuously and thus mechanical energy (rotational K.E. is obtained.)

The direction of rotation of the armature coil could be determined with the help of Fleming’s left-hand rule. Due to this fact, the left-hand rule is also called the ‘rule of motor’.

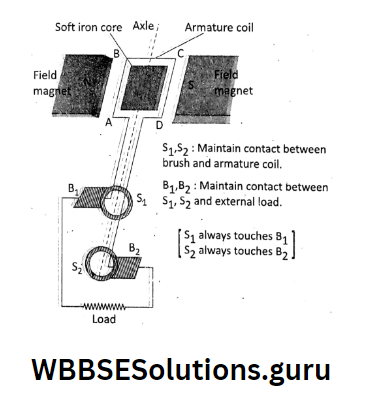
A rectangular coil made of insulated Cu wire, called armature coil, ABCD is placed in between two ponies of a strong magnet NS.

The ends A and D of the coil are connected to a commutator made of Cu which has two split parts R₁ and R₂.

This combination is mounted on a shaft so that it is capable of rotating around the shaft. A pair of carbon brushes and  B₂ press gently against R₁ and R₂ respectively.

A d. c. source is connected across the carbon brasses B₁ and B₂. Here note that R₁,R₂ is connected with the armature coil and B₁, B₂ with the external circuit.

Working: When current is passed through the armature coil in the direction DCBA, then according to Fleming’s left-hand rule, the force on the arm AB acts in the inward direction and that force acts on the arm CD in the outward direction.

Force on sides BC and AD are zero as these are directed along the magnetic field. The equal and opposite forces acting on arms AB and CD form a couple.

This couple creates rotational motion in the coil in the anticlockwise direction. While rotating, it, the coil begins to rotate and the arm AB comes out and the arm CD goes in.

When the coil reaches a vertical position, the carbon brushes lose contact with the commutator and momentarily the current gets cut off.

However, due to the inertia of motion, the coil continues rotating in the same direction.

After half rotation, R₁ comes in contact with B₂ and R₂ with B₁ At this position the force on the arm CD acts in the outward direction, and on the arm AB it acts in an inward direction.

Due to this, the coil continues rotating in the same direction. The strength of an electric motor can be Increased by

1. Increasing the number of turns in the armature coil,
2. Increasing the strength of current through the armature,
3. Increasing the area of the coil and

Increasing magnetic field strength by inserting a soft iron core inside the armature coil. Because soft iron has the property to get magnetized easily.

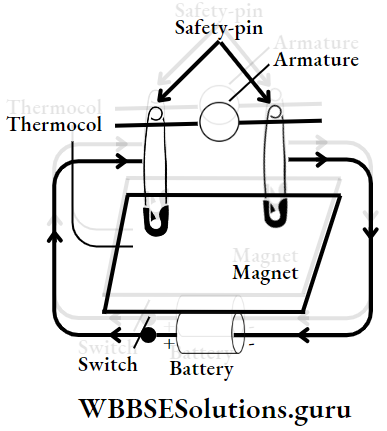
Activity: To make a model of a motor using a battery, magnet, and wires: Wrap a 3-4ft long insulated copper wire around a hollow pipe in 25-30 turns.

Ejecting the pipe, bring out the tightly packed coil. This coil acts as an armature. Strip out the insulation wire from two ends of the coil wire.

Two safety pins are inserted in a thermocol tightly with a gap from one another. Safety pins combined act as a commutator.

Two ends of the coil are brought in to support over two safety pins such that there is free space for rotation of the coil.

Keep a disc magnet into the thermocouple, just below the coil Then, + ve and -ve terminals of an electric cell through a switch are connected with two ends of the safety pins.

When the switch is made ON, current flows through the coil and it starts rotating and as soon as the switch is OFF, the rotation stops. This is a hand-made motor. Can it work with an alternating current? No.

WBBSE Chapter 6 Current Electricity Electromagnetic Induction Concept Of Induced EMF And Induced Current

We knew what happens when a current-carrying wire is placed in a magnetic field. Oersted’s experiment proved that electric current produces a magnetic field.

Can the reverse be also true? Let us see what will happen, as per the activity

Simple Demonstration: Take a coil with which a current-sensitive galvanometer (G) is connected in series having no source and a simple bar magnet (for which the direction of magnetic field lines or magnetic flux is from the N-pole to the S-pole).

Now, move either pole of the magnet (N or S) towards or away from the coil. A deflection in G-needle is seen (either towards the left or right).

But, if the magnet’s motion is stopped, G- the needle does not deflect. Keeping the magnet fixed, when the coil is moved towards or away from the magnet, deflection in G-needle is also seen.

Make the faster motion of either the magnet or the coil, and faster deflection in the G-needle is seen.

Replacing the magnet with a current-carrying coil, the same type of result is obtained.
Does it happen because of motion?

Actually, when there is a relative motion between a coil and a magnet, the magnetic field lines linking to the cross-section of the coil (i.e. magnetic flux) change (increases/decreases), and because of this change, an emf (potential difference) is induced across two ends of the coil.

When the motion is stopped, no change in magnetic flux takes place, i.e., the existence of emf lasts as long as there is a change in magnetic flux.

The emf produces an electric current called induced current, for which G-needle deflects, and it lasts as long as a change in magnetic flux takes place.

The phenomenon is known as electromagnetic induction. As a whole, mechanical energy (or work) is directly converted into electrical energy.

What a surprising fact Without using a voltage source (d.c.), electric current can be obtained In 1822, Michael Faraday, an English scientist, first time invented it.

Electromagnetic induction is a milestone discovery of Faraday’s laws of electromagnetic induction:

Faraday’s First Law: Whenever there is a change in the magnetic flux linked with a conductor, an e.m.f. is induced in the conductor, as long as there is a change in the magnetic flux.

If the conductor forms a closed coil, an induced current flows through it.

Faraday’s Second Law: The magnitude of induced e.m.f. is directly proportional to the rate of change of magnetic flux linked with the conductor or coil.

Lenz’s law as a consequence of conservation of energy: when the N-pole of the magnet is brought towards the coil, an induced current would flow through the coil such that the magnetic flux would decrease.

This is possible if the induced current would try to oppose the increase of magnetic flux i.e. an N-pole is induced at the face of the coil which opposes the motion of the N-pole of the magnet approaching the coil.

The mechanical energy spent in doing work against such opposing force is transformed into electrical energy, due to which a current flows in an anti-clockwise direction in the coil.

Similarly, when the S-pole of the magnet is brought towards the coil, the induced current flows in a clockwise direction.

Here, in the absence of external force, the K.E. of the moving magnet decreases while the P.E. of the coil increases at the same rate.

Hence, we can conclude that Lenz’s law is based on the law of conservation of energy.

Remember: Lenz’s law is one of the fundamental laws of the universe.

Faraday’s First Law: States the cause of induced EMF or current in a closed coil.

Faraday’s Second Law: States how much emf or current is induced.

Lenz’s Law: States the direction of induced emf or current.

WBBSE Chapter 6 Current Electricity Direct Current (D.C.) AND Alternating Current (A.C.)

Advantages of a.c. over d.c.: In practical use, generally, 220V a.c. is preferred, but not the d.c. The reason is that the a.c.

voltage can be increased or decreased by the use of a step-up or step-down transformer. It reduces the loss of electrical energy in the transmission lines.

On the other hand, the D.C. voltage can not be increased or decreased and this causes a huge loss of electrical energy in the line wires while passing d.c.

But in machines where big-size motors are used (to run trains,. tram), d.c. is more useful.

WBBSE Chapter 6 Current Electricity Electric Generator

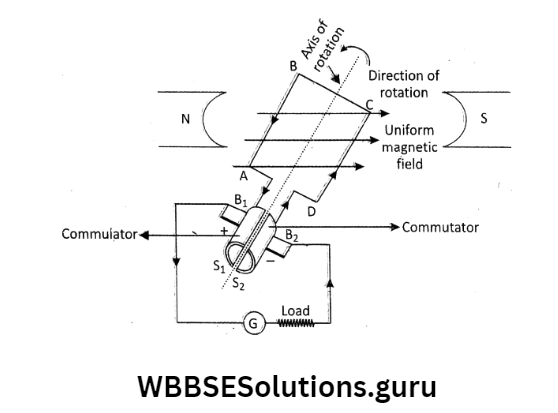
A.C. generator: A.C. generator is a device that converts mechanical energy into electrical energy, working ‘according to the principle of electromagnetic induction.

There are two kinds of generators

1. A. C. generator and
2. D. C. generator.

How does it work? : In an A.C. generator, a rectangular coil is rotated in a magnetic field, because of which the magnetic flux changes with time, and an e.m.f.

Is induced between the ends of the coil. The basic construction of the main parts of an A.C. generator is

an armature coil ABCD made of insulated Cu wire wound over a soft iron core,

A field magnet,

Two co-axial slip rings and S₁ S₂, Two- carbon brushes B₁ B₂. This arrangement is mounted on an axle.

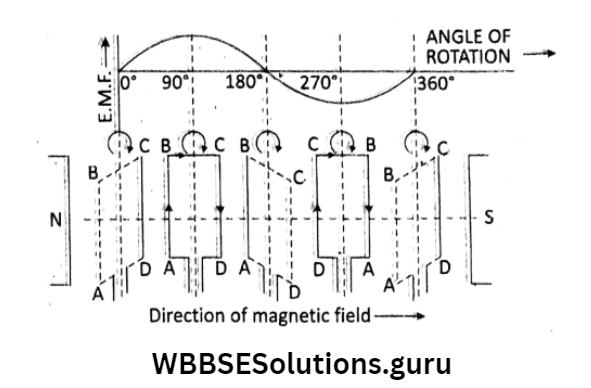
Working: Initially suppose when the armature coil starts rotating, the angle between the direction of magnetic flux lines and the axis of the coil is 0°.

There is no emf induced in the coil, because of no flux change. If the coil is rotated clockwise from 0° to 90°, maximum emf is induced in the coil.

When the coil is further rotated to 180°, the induced emf again becomes zero.

When the coil turns from 180° to 270°, then magnetic flux lines change in the opposite direction, and maximum emf is produced in the opposite direction.

Again when the coil turns to 360°, the rate of flux change again becomes zero, then emf also becomes zero.

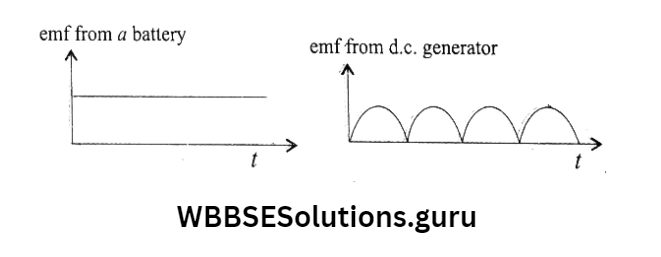
During rotation of the coil, the arms AB and CD interchange their positions periodically. Thus the e.m.f. or current changes its polarity as well as magnitude periodically. It is called the alternating e.m.f.

The frequency of a. c. produced in a generator is determined by the number of rotations of the armature coil in one second.

In our country, the frequency of A.C. is 50 Hz. That is, the current changes its direction 100 times in 1 second.

The maximum value of induced e.m.f. in the armature coil of an A. C. dynamo can be increased by

1. Increasing the area of the cross-section of the coil,
2. Increasing the number of turns in the coil and
3. Increasing the speed of rotation of the coil,
4. Increasing the magnetic field strength.

D.C. generator: Like an a.c. generator, a d. c. generator has a field magnet and an armature coil.

The co-axial slip rings are replaced by two half-cylindrical slip rings which act as a commutator The commutator rotates with the rotation of the armature coil.

In each half-turn, the parts of the commutator pass from one brush to another. Positions of S_{1; and} S₂ reverse but the brushes B₂ stay in the same position so that the output is always in the same direction.

In d.c. the generator also the induced emf is a.c. in nature but this emf is converted into d.c. by using the commutator.

In d.c. generator the current flows in the external circuit only in one direction.

The basic principle of thermal and hydroelectric power generation:

Thermal power generation: In a thermal power station, the heat produced by the combustion of fossil fuel (coal) helps to boil water at very high pressure.

When the steam is allowed to rotate the blades of a turbine, the shaft of the turbine rotates at a very high speed. It helps to rotate the armature coil of the a.c. generator and produces thermo-electricity. Here mechanical energy is converted into electrical energy.

(2) Hydroelectric power generation: Hydroelectricity or hydroelectric power is produced by utilizing the mechanical energy of a high-speed stream of water.

In hilly areas, the water confined in a dam is released to flow through a tunnel at a very high speed, which then falls upon the blades of the turbine, and the turbine rotates.

In the next stage, the a.c. a generator connected to the rotating turbine produces hydroelectricity.

WBBSE Chapter 6 Current Electricity Domestic Electrical Circuit Components Used In Domestic Electrical Circuit

Switch: An electric switch is an on-off device for current in an electric circuit when desired. Commonly used electric switches are lever type (push button type switch).

A switch is always connected to the live wire. In the household circuits, a 5A switch is used for light/fan, and a 10 A / 15 A switch for fridge/washing machine/ geyser.

The main switch is used near the meter board. It has a live wire and a neutral wire. This switch keeps household circuits protected.

Three-pin plug: In a three-pin plug, the top thick pin is for earthing connection, the left-hand pin is for life and the right-hand pin is for neutral connection.

The earth pin is thicker than the other two pins in a three-pin plug: The earth pin is made thicker so that it can be connected first. This ensures the safety of the user.

Moreover, being thicker, the earth pin cannot be inserted into the hole of the socket for a live or neutral connection.

Holes in a socket: The upper bigger hole in the socket is for earth connection, the right-hand hole is for connection to the live wire, and the left-hand hole is for connection to the neutral wire.

Live wire, neutral wire: In domestic electrical circuits, there are three wires—Live or phase (220 V), neutral (0V), and earth (0V). The live wire carries the incoming electricity at 220V, so it is very dangerous.

The neutral wire is tied at zero potential. It is taken as a reference potential. The neutral completes the circuit, as it returns electricity to the generator after passing through the appliance.

The earth wire is connected to the earth and is used for precaution of the appliance.

Earthing of electrical appliance: By earthing an electrical appliance such as electric iron, heater, geyser, etc.

it is connected to a low potential. Ultimately by connecting it directly with a local earthing wire.

Local earthing: For local earthing, a thick copper wire kept inside a hollow insulating pipe is buried 2-3m deep in the earth.

It is connected to a thick copper plate of dimensions about 50 cm × 50 cm surrounded by a mixture of charcoal and salt.

If at any stage the iron/heater gets directly connected with the live wire, then the earthing system automatically maintains zero potential and saves from dangerous accidents.

The body/casing of an electrical appliance is always earthed.

If the switch is connected to the neutral wiring electrical appliance remains connected to the live wire and acquires supply voltage, even if the switch is off.

If a person touches the switch, the body comes in contact with the live wire of the appliance. Under such circumstances, the person may get a fatal shock.

To avoid accidents, the switch should always be connected to the live wire.

Color-coding of wires: According to the new international convention, the color coding of wires.

WBBSE Chapter 6 Current Electricity Household Circuits

In household wiring, all the appliances (e.g. bulbs, fans, TV, geyser, etc.) are connected in parallel at the mains, each with a separate switch.

A bulb, and a fan (with regulator) are connected parallel to the distribution box. For each branch line, a separate fuse and switch are connected to the live wire at the distribution box.

Neutral wire and earth wire are common to all branches or appliances.

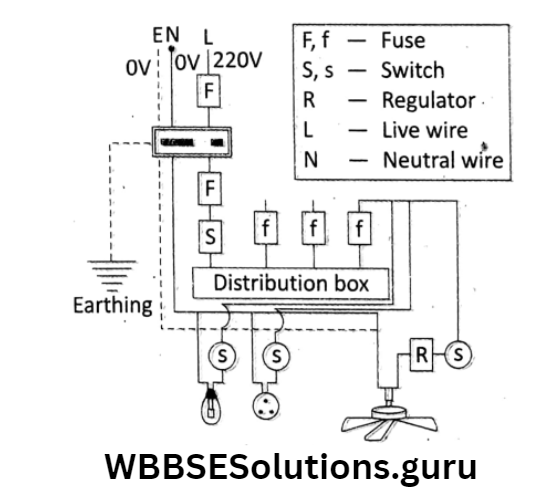
The advantage of the parallel combination is all the appliances get the main voltage and if any one of the appliances goes out of work the electric supply to other appliances does not get affected and they remain functioning properly at the same voltage,

In parallel combination, R_eq. decreases. So heat loss also decreases.

An electric shock may be caused by an electrical appliance due to poor insulation of the wires.

It is very dangerous to test electrical instruments using domestic power lines.

Activity:  A simple model of an electrical circuit using a battery as a source.