WBBSE Solutions For Class 7 Maths Geometry Chapter 3 Properties Of Triangle

Geometry Chapter 3 Properties Of Triangle

Question 1. Choose the correct answer

1. If the measurement of the angle of a triangle is 100° then the triangle is

1. Right-angled triangle
2. Acute angled triangle
3. Obtuse angled triangle
4. None of these

∴ The option (3), an obtuse-angled triangle ≤ 90° to 2120° is an obtuse angle.

2. If the measurement of one angle is equal to the sum of measurements of other two angles then the triangle is

1. Acute angled
2. Right-angled
3. Obtuse angled
4. None of these

Read and Learn More Class 7 Maths Solutions

Class 7 Geometry Chapter 3 Questions

∴ The option (2) Right angled triangle is the correct answer

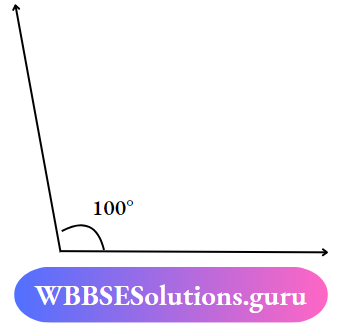
Greater than 90° to equal to 120° the angle is called obtuse Angle

Hypotenus = side+ Adjacent

If the measurement of two angles is x and y then the measurement of the third angle is

1. (X-Y)°
2. (x+y)°
3. 180-(2+1)°
4. {180 -(x-x)}

∴ The option (3) is the correct answer

A sum of Angles in a triangle is 180°

Here we have two angles given x° and y°

∴ x° + y° + third angle = 180°

third angle = 180° – (x°+ y°)

WBBSE Class 7 Maths Geometry Solutions

Question 2. write the true or false.

1. Obtuse triangle has two obtuse angle

→ False

∵ The obtuse angle lies between 90° to 120°

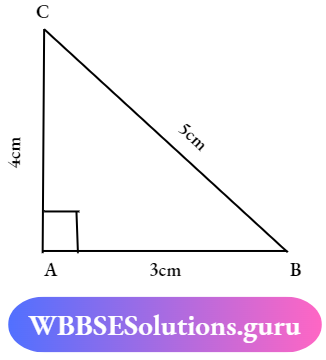
2. If the length of the three sides of a triangle 3 cm, 4cm, and 5cm then the triangle is a right-angled triangle

→ True

3. The measurement of the three angles of an isosceles right angled triangle is 45°, 45° and 90°

→ True

In an Isosceles right angled triangle two sides (or) two angles are equal then the triangle is Isosceles and having 90° is called an Isosceles right isosceles-angled triangle.

Class 7 Geometry Textbook Solutions

Question 3. Fill in the blanks

Question 1. The median of a triangle is ______
Answer: Concurrent.

Question 2. The point of intersection of perpendicular bisectors of a triangle is called ______
Answer: Orthocentre

Question 3. The height and median of a ______ are equal
Answer: Equilateral triangle

Question 4. If the ratio of measurement angles of a twangle is 3:4:5 then write the name of the triangle.
Solution:

The Sum of angles in a triangle is 180°

Angles of a triangle are in a ratio of 3:4:5

Let’s denote the angles are 3x,48,5x

3x+4x+5x=180°

12x = 180°

x = \(\frac{180}{12}\)

x = 15

∴ 3x = 3 ×15 ⇒ 45°
་
4x = 4 ×15 ⇒ 60°

5x = 5 ×15 ⇒ 75°

By observing that all three angles lie between 0° to 9°

∴ The triangled formed by the angles are Acute angle triangle

Class 7 Maths Geometry Problems

Question 5. The length of the base of a triangle is 12cm and its height is 10cm Find its area.
Solution:

Given:-

Base = 12cm

Height = 10cm

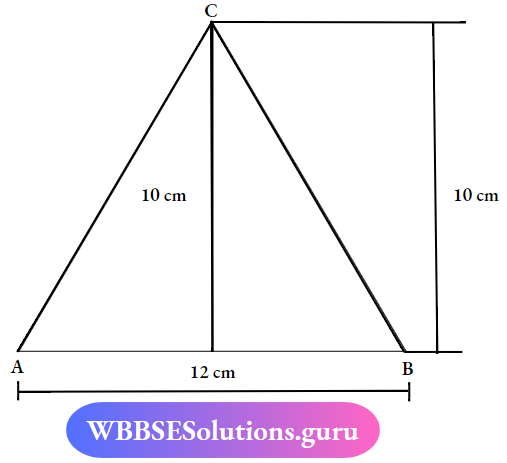
Area of triangle = \(\frac{1}{2}\) [Base x Height]

⇒ \(\frac{1}{2}\)[12×10]

⇒ \(\frac{1}{2}\)[120]

Are of triangle = 60 sqcm

Question 6. If the area of a triangle is 100sqm and length. of its base is 20cm find its altitude.
Solution:

Given:

Area of triangle = 100 sq cm

Length of base = 20cm

Altitude =?

Area of triangle = \(\frac{1}{2}\)[Base × Height]

100 = [\(\frac{20}{2}\) × Height ]

100 × \(\frac{2}{1}\) = [\(\frac{20}{2}\) × Height]

200 = 10 × Height

⇒ \(\frac{200}{20}\) = Height

200 = Height

Height Altitude = 20cm ⇒ 20cm

∴ The Altitude of a triangle is 20cm

Class 7 Geometry Formulas

Question 7. If the length of hypotenuse use and the length of one side are 20cm and 16cm respectively. Find the length of the third side.
Solution:

Given

Length of hypotenuse = 200m

Length of one side = 16cm

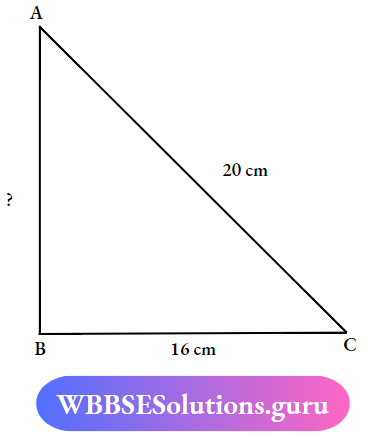
From Pythagoras Theorem

(Hypotenuse)² = (Side)² + (side)²

(20)² = (16)²+(Side)²

(20)² – (16)² = (Side)²

(20+16) (20-16) =(Side)²

36 × 4 = (Side)²

144 = (Side)²

side = √144

Side = 12

∴ The length of the third side is 12cm

Class 7 Geometry Chapter 3 Explanation

Question 8. If the length of three sides of a triangle is (m²-n²) unit, 2mn unit, and (m²+n²) unit. then Write the name of the triangle.
Solution:

Given:-

The first side of the triangle = (m²-n²) unit.

The second side of the triangle = 2mn unit

The third Side of the triangle = m²+n² unit

m²+n² is the largest side.

m²+n² will always be greater than the other two sides, given that m and n are positive integers.

Apply Pythagoras theorem

(m² + n²)² = (m²-n²)² + (2mn)² + (m²+n²)²

m⁴+2m²n²+n⁴ = m⁴ – 2m²n² + n⁴ + 4m²n²

m⁴+2m²n²+n⁴ = m⁴ +n⁴+2m²n²

(m²+n²)² = (m²+n²)²

∵ The sum of the squares of the two smaller sides equals the square of the largest side, of a triangle. satisfies the Pythagoreus theorem.

A triangle with sides (m²-n²) unit, 2mm unit, and (m²+n²) is a right angled triangle