Geometry Chapter 6 Parallel Lines And Transversal
Question 1. What are parallel lines?
Solution:
Parallel lines: If two straight lines on the same Plane do not intersect when produced in any direction the two straight lines are said to be parallel to one another.
In the Below Figure the straight line, AB, CD, and EF are parallel to each other i.e., AB || CD || EF

Question 2. what are vertically opposite Angles?
Solution:
Read and Learn More Class 7 Maths Solutions
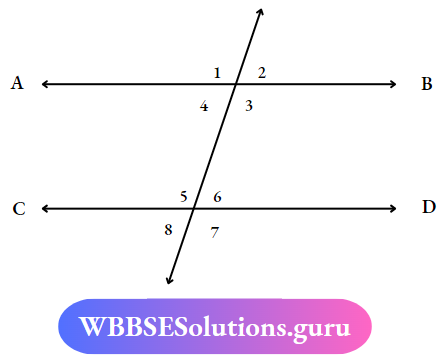
Vertically Opposite Angles: If two straight lines intersect at a point, the angles formed on the opposite sides of the common point (vertex) are called vertically opposite angles. Here are two straight lines AB, CD interest at ‘O’. ∠AOC, ∠BOD are two vertically opposite angles.

Also LAOD, ∠Boc are two vertically opposite angles.

WBBSE Class 7 Maths Geometry Chapter 6
Question 3. what are corresponding angles?
Solution:
Corresponding Angles: Two angles lying on the same side of the transversal are known as corresponding angles if both lie either above are below the two given lines.

There are four pairs of corresponding angles.
(∠1, ∠5), (∠2,∠6), (∠8,∠4), and (∠7, ∠3).
Question 4. what is alternate Angles?
Solution:
Alternate Angles: The pair of interior angles on the opposite side of the transversal are called alternate angles.
There are two pairs of alternate angles (∠4,∠6), (∠3,∠5)
Class 7 Geometry Chapter 6 Exercise Solutions
Question 5. From the Figure write down the pairs of corresponding angles, alternate angles, and vertically opposite angles.
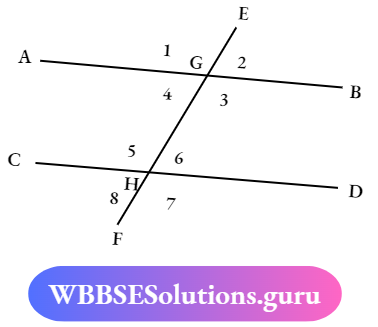
Corresponding Angles:- (∠1,∠5), (∠2, ∠6) (∠8,∠4), and (∠7, ∠3).
Alternate Angles: (∠4, ∠6) and (∠3, ∠5).
Vertically opposite Angles: (∠AGE, ∠OHF) (∠EGB, ∠CHF)
Question 6. In the adjacent Figure AB II CD Find the value of (∠BGH + ∠GHD)
Solution:
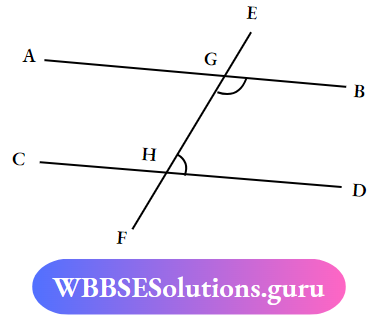
∴ The Sum of the measurement of two interior angles on the same side of the transversal is 180°
∴ ∠BGH + ∠GHD = 180°
Class 7 Maths Chapter 6 Geometry PDF
Question 7. In the adjacent Figure, ABIICD, IF ∠EGB= 40° then find the value of ∠AGH, ∠AGE, ∠BGH, ∠GHD, ∠GHC, ∠CHF, ∠DHF
Solution:

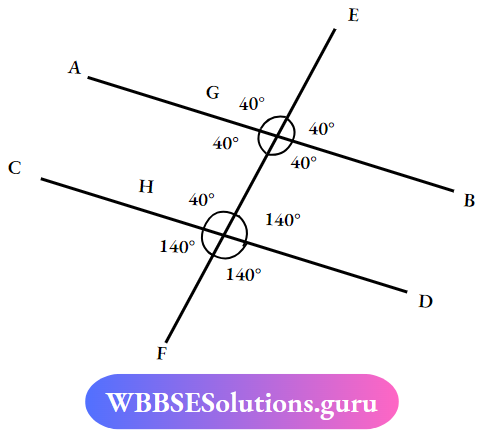
∠EGB = 40°
∠AGH = 40° Transversal the corresponding angles are equal.
∠AGE = 40° is an external angle to ∠EGB. exterior angle theorem ∠AGE = ∠EGB
∠BGH = 40° LBGH is the corresponding angle to ∠EGB.∠BGH = ∠EGB = 40°
∠GHD = 140° The corresponding angles on the same side ∠GHD+ ∠BGH = 180° ∠GHD = 180 – 40 = 140°
∠GHC = 40° LGHC corresponds to ∠AGH. ∠GHC = ∠AGH =40°
∠CHF = 140°
∠DHF = 140° ∠DHF Corresponds to ∠GHD.
∠DHF = ∠GHD = 140°
