WBBSE Solutions For Class 8 Maths Algebra Chapter 2 Multiplication And Division Of Polynomials

Algebra Chapter 2 Polynomials

The Algebraic expression having one or more terms is called Polynomial Expression.

Multiplication of Algebra

Example 1. Let the length and breadth of a rectangle are (3x + 2y) unit and (x – 4y) unit respectively.

Solution: Area is (3x + 2y) x (x – 4y) sq. unit

= {3x (x – 4y) + 2y (x – 4y)} sq. unit

Read and Learn More WBBSE Solutions For Class 8 Maths

= (3x² – 12xy + 2xy – 8y²) sq. unit = (3x² – 10xy – 8y²) sq. unit

Example 2. Multiplication: (a² + ab + b²) by (a² – ab + b²)

1. Multiplicand: a² + ab + b²
2. Multiplier: a² – ab + b²

Solution: Multiplication:

The product = a⁴ + a²b² + b⁴

Alternating Method:

(a² + ab + b²) (a² – ab + b²)

= a² (a² – ab + b²) + ab (a² – ab + b²) + b² (a² – ab + b²)

= a⁴  – a³b + a²b² + a³b – a²b² + ab³ + a²b² – ab³ + b⁴ = a⁴+ a²b² + b⁴

WBBSE Class 8 English Functional Grammar	WBBSE Class 8 English Reading Skills
WBBSE Solutions For Class 8 English	WBBSE Solutions For Class 8 Maths

 

Example 3. Find the product by successive multiplication. (x² – 1), (x² + 2x² – 5), (5 – x³ + x⁴)

Solution:

∴ The required product = x⁹ + x⁸ – 3x⁷ – 6x⁶ + 125x⁵ + 15x⁴ – 10x³ – 35x² + 25

Example 4. Find the continued product of (a + b + c), (a – b + c), (a + b – c) and (b + c – a)

Solution:

∴ The required product = 2a²b² + 2b²c² + 2c²a² – a⁴ – b⁴ – c⁴

Example 5. Find the product by successive multiplication: \(\left(\frac{a}{b}+\frac{b}{c}\right),\left(\frac{b}{c}+\frac{c}{a}\right),\left(\frac{c}{a}+\frac{a}{b}\right)\)

Solution: \(\left(\frac{a}{b}+\frac{b}{c}\right)\left(\frac{b}{c}+\frac{c}{a}\right)\left(\frac{c}{a}+\frac{a}{b}\right)=\left\{\frac{a}{b}\left(\frac{b}{c}+\frac{c}{a}\right)+\frac{b}{c}\left(\frac{b}{c}+\frac{c}{a}\right)\right\}\left(\frac{c}{a}+\frac{a}{b}\right)\)

= \(\left(\frac{a}{c}+\frac{c}{b}+\frac{b^2}{c^2}+\frac{b}{a}\right)\left(\frac{c}{a}+\frac{a}{b}\right)\)

= \(\frac{a}{c}\left(\frac{c}{a}+\frac{a}{b}\right)+\frac{c}{b}\left(\frac{c}{a}+\frac{a}{b}\right)+\frac{b^2}{c^2}\left(\frac{c}{a}+\frac{a}{b}\right)+\frac{b}{a}\left(\frac{c}{a}+\frac{a}{b}\right)\)

= \( 1+\frac{a^2}{b c}+\frac{c^2}{a b}+\frac{a c}{b^2}+\frac{b^2}{a c}+\frac{a b}{c^2}+\frac{b c}{a^2}+1\)

= \(2+\frac{a^2}{b c}+\frac{b^2}{c a}+\frac{c^2}{a b}+\frac{a b}{c^2}+\frac{b c}{a^2}+\frac{c a}{b^2}\)

Example 6. Simplify: (a – b) (a² + ab + b²) + (b − c) (b² + bc + c²) + (c − a) (c² + ac + a²)

Solution:

Given

(a – b) (a² + ab + b²) + (b − c) (b² + bc + c²) + (c− a) (c² + ca + a²)

= a (a² + ab + b²) – b (a² + ab + b²) + b (b² + bc + c²) – c (b² + bc + c²) + c (c² + ca + a²) – a (c² + ca + a²)

= a³ + a²b + ab² – a²b – ab² – b³ + b³ + b²c + bc² – b²c – bc² – c³ + c3 + c²a + a²c – c²a – a²c – a³ = 0

Example 7. Simplify: \(\left(a^{-1}+b^{-1}\right)\left(a^{-1}-b^{-1}\right)\left(a^{-2}+b^{-2}\right)\)

Solution:

Given that

\(\left(a^{-1}+b^{-1}\right)\left(a^{-1}-b^{-1}\right)\left(a^{-2}+b^{-2}\right)\)

= \(\{\left(a^{-1}\left(a^{-1}-b^{-1}\right)+b^{-1}\left(a^{-1}-b^{-1}\right)\right\}\left(a^{-2}+b^{-2}\right)\)

= \(\left(a^{-2}-a^{-1} b^{-1}+ a^{-1} b^{-1}-b^{-2}\right)\left(a^{-2}+b^{-2}\right)\)

= \(\left(a^{-2}-b^{-2}\right)\left(a^{-2}+b^{-2}\right)\)

= \(a^{-2}\left(a^{-2}+b^{-2}\right)-b^{-2}\left(a^{-2}+b^{-2}\right)\)

= \(a^{-4}+q^{-2} b^{-2}-a^{-2} \cdot b^{-2}-b^{-4}\)

= \(a^{-4}-b^{-4}\)

\(\left(a^{-1}+b^{-1}\right)\left(a^{-1}-b^{-1}\right)\left(a^{-2}+b^{-2}\right)\) = \(a^{-4}-b^{-4}\)

Example 8. Simplify: (a + b + c) (a² + b² + c² – ab – bc – ca)

Solution:

Given

(a + b + c) (a² + b² + c² – ab- bc – ca)

= a (a² + b² + c² – ab- bc – ca)

+ b (a² + b² + c² – ab- bc – ca)

+ c (a² + b² + c² – ab- bc – ca)

= a³ + ab² + ac² – a²b – abc – a²c

+ a²b + b³ + bc² – ab² – b²c – abc

+ b²c + c³ – abc – bc² – ac²

(a + b + c) (a² + b² + c² – ab- bc – ca) = a³ + b³ + c³ – 3abc

Algebra Chapter 2 Division

Method of division are of two types

1. Exact division
2. Inexact division

In case of Exact division, the remainder zero.

Here Dividend = Divisor x Quotient.

In case of Inexact division, after completion of division, we have quotient and remainder.

Here Dividend = Divisor x Quotient + Remainder.

Example 1. Divide (x² – 4x – 5) by (x – 5)

1. Divisor = (x- 5)
2. Dividend = x² – 4x – 5

Solution:

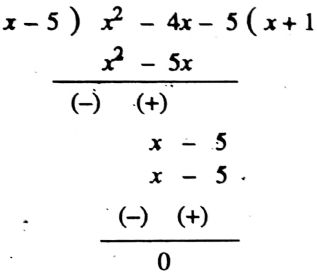
∴ The quotient is (x + 1) and remainder is 0.

Example 2. Divide (5x³y² – 7x²y³ + 3xy⁴) by xy⁴

Solution:

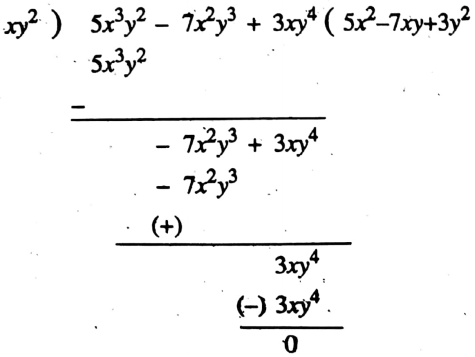
∴ The quotient is 5x² – 7xy + 3y² and remainder is 0.

Example 3. Divide the first expression by the second:

1. (a³ + b³ + c³ – 3abc), (a + b + c)
2. (x⁴ – 2x³ – 15x² + 16x + 35), (x² + x – 7)

Solution:

∴ Quotient = a² + b² + c² – ab- bc – ca

Remainder = 0

2.

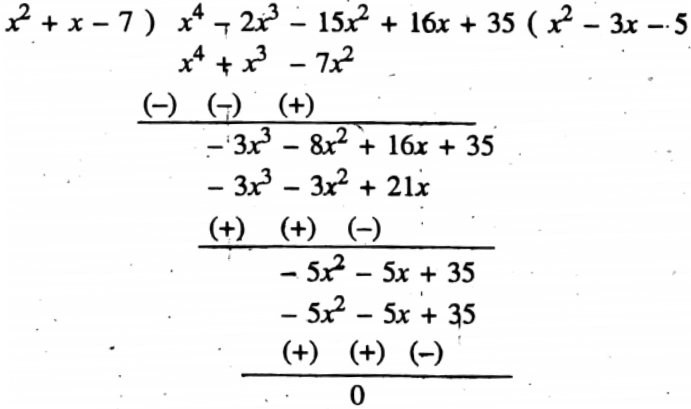
∴ Quotient = x² –  3x – 5

Remainder = 0

Example 4. Divide (a – b) by \(a^{\frac{1}{3}}-b^{\frac{1}{3}}\)

Solution:

∴ Quotient = \(a^{\frac{2}{3}}+a^{\frac{1}{3}} b^{\frac{1}{3}}+b^{\frac{2}{3}}\)

Remainder = 0

Example 5. Find the quotient and the remainder of the following:

1. (x³ + x² + 25) by (x + 3),
2. (81x⁴ + 4) by (3x – 1)
3. (9a² – 4a³ – 5 + a4 -19a) by (7 + a² – a)

Solution:

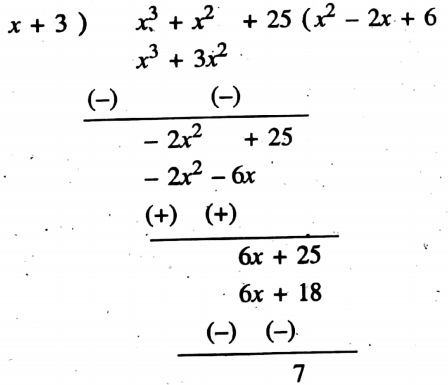
∴ The required quotient = x² – 2x + 6 and remainder = 7

2.

∴ Quotient = 27x³ + 9x² + 3x + 1

Remainder = 5

3. Dividend = 9a² – 4a³ – 5+ a⁴ – 19a

= a⁴ – 4a³ + 9a² – 19a – 5 [In descending power of a]

Divisor = 7 + a² – a

= a² – a + 7 (In descending power of a)

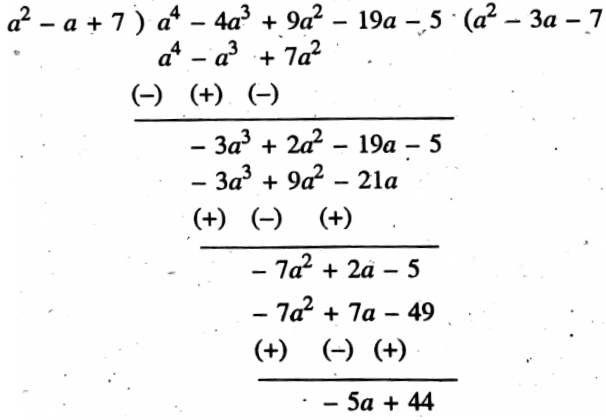
∴ The Quotient = a² – 3a-  7

Remainder = 44-5a

Example 6. Divide (6x² + 11xy + 6y²) by (3x – 2y)

Solution:

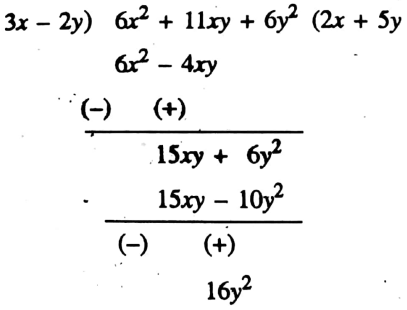
∴ Quotient = 2x + 5y

Remainder = 16y²

Example 7. In a division problem the divisor is (x² – 3x + 5), the quotient is (2x – 7) and remainder.

Solution: Dividend = Divisor x Quotient + Remainder

= [(x² – 3x + 5) × (2x-7)] + (x + 3)

= [ 2x³ – 7x² – 6x² + 21x + 10x – 35] +[ x + 3 ]

= 2x³ – 13x² + 32x – 32

Example 8. Choose the correct answer:

1. (x – 3)(x + 2) =

1. x² – 5x – 6
2. x² – x – 6
3. x² – x + 6
4. x² -5x + 6

Solution: (x-3) (x+2)

= x(x+2)- 3(x+2)

= x² + 2x – 3x – 6 = x² – x – 6

∴ The correct answer is 2. x² – x – 6

2. (8x⁸ – 8x² – 36x) ÷ 4x =

1. 2x⁸ – 2x² – 9
2. 2x⁸ – 8x – 36
3. 2x⁷ – 2x – 9
4. 2x⁷ – 2x – 18

Solution: \(\frac{8 x^8-8 x^2-36 x}{4 x}=2 x^7-2 x-9\)

∴ The correct answer is 3. 2x⁷ – 2x – 9

3. (x² – 14x + 45 ÷ (x – 5) =

1. x – 9
2. x + 5
3. 9 – x
4. x + 9

Solution:

∴ So the correct answer is 1. x – 9

Example 9. Write ‘True’ or ‘False’:

1. (x – a) (x – b) (x – c)…. (x − z) = 1

Solution: (x – a) (x – b) (x – c)…… (x – z)

= (x − a) (x – b) (x − c)….. (x – x) (x − y) (x − z)

= (x – a) (x – b) (x – c)…. (0) (x − y) (x – z) = 0

∴ The statement is false.

2. \(\left(\frac{a}{b}+\frac{c}{d}\right)\left(\frac{a}{b}-\frac{c}{d}\right)\left(\frac{a^2}{b^2}+\frac{c^2}{d^2}\right)\)=\(\frac{a^4}{b^4}-\frac{c^4}{d^4}\)

Solution:

Given that

\(\left(\frac{a}{b}+\frac{c}{d}\right)\left(\frac{a}{b}-\frac{c}{d}\right)\left(\frac{a^2}{b^2}+\frac{c^2}{d^2}\right)=\left(\frac{a^2}{b^2}-\frac{c^2}{d^2}\right)\left(\frac{a^2}{b^2}+\frac{c^2}{d^2}\right)\)

= \(\left(\frac{a^2}{b^2}\right)^2-\left(\frac{c^2}{d^2}\right)^2=\frac{a^4}{b^4}-\frac{c^4}{d^4}\)

∴ So the statement is true.

3. (x² + 11x + 27) ÷ (x + 6) = x + 5 + \(\frac{(-3)}{x+6}\)

Solution:

∴ \(\left(x^2+11 x+27\right) \div(x+6)=(x+5)+\left(-\frac{3}{x+6}\right)\)

∴ So the statement is true.

Example 10. Fill in the blanks:

1. \((-2 a)^2 \times(-3 a)^3 \times\left(-\frac{1}{3} a\right)^3=\)________

Solution: \((-2 a)^2 \times(-3 a)^3 \times\left(-\frac{1}{3} a\right)^3\)

= \(4 a^2 \times-27 a^3 \times-\frac{1}{27} a^3=4 a^2\)

2. (x² + xy + y²) (x − y) = ________

Solution: (x² + xy + y²) (x − y)

= ( (x² + xy + y²) × (x))
– ((y) × (x² + xy + y²))

= x³ + x²y + xy²  – x²y – xy²  – y³

= x³ – y³

(x² + xy + y²) (x − y) = = x³ – y³

3. (5x² – 2x – 3) ÷ (x – 1) = ________

Solution:

Quotient is (5x+3).

(5x² – 2x – 3) ÷ (x – 1) = (5x+3).