WBBSE Solutions For Class 8 Maths Algebra Chapter 5 HCF And LCM Of Algebraic Expression

Algebra Chapter 5 HCF And LCM Of Algebraic Expression

To find the H.C.F. (Highest Common Factor) or G.C.D. (Greatest Common Divisor) the given expressions should first be resolved into elementary factors.

The H.C.F. or G.C.D. will be the product of the common elementary factors of the highest power that divide each of the given expressions.

Algebra Chapter 5 HCF And LCM Of Algebraic Expression Examples

Example 1. Find the H.C.F. of 4a²b², 12ab³ and 20a²b⁴.

Solution:

H.C.F. of 4a²b², 12ab³ and 20a²b⁴ is 2 x 2 x a x b x b or 4ab²

Alternate method:

G.C.D. of 4, 12 and 20 = 4

Lowest power of a is 1 and b is 2 in the expression 4a²b², 12ab^3, and 20a²b⁴.

∴ The required G.C.D. is 4a¹b² or 4ab².

Read and Learn More WBBSE Solutions For Class 8 Maths

Example 2. Find the G.C.D. of the following algebraic expression. 24x³yz², 18x²y³z³, 36x⁴y²z⁴

Solution:

The required G.C.D. = 2 x 3 x x x x x y x y x z x z = 6x²y²z²

WBBSE Class 8 English Functional Grammar	WBBSE Class 8 English Reading Skills
WBBSE Solutions For Class 8 English	WBBSE Solutions For Class 8 Maths

 

Example 3. Find G.C.D. of the following expressions:

1. a² + 3a + 2, a² + 4a + 3, a² + 5a +6
2. 3 (a + b)³, 6 (a + b)², 9(a² -b²)
3. x³ – 3x² – 10x, x³ + 6x² + 8x, x⁴ – 5x³ – 14x²

Solution:

1. 1st expression,

a² + 3a + 2

= a² + (2 + 1) a + 2 = a² + 2a + a +2

= a (a + 2) + 1 (a + 2) = (a + 2)(a + 1)

a² + 3a + 2, a² + 4a + 3, a² + 5a +6 = a (a + 2) + 1 (a + 2) = (a + 2)(a + 1)

2nd expression,

a² + 4a + 3

= a² + (3 + 1) a +3 = a² + 3a + a + 3

= a (a + 3)+ 1 (a + 3) = (a + 3)(a + 1)

3 (a + b)³, 6 (a + b)², 9(a² -b²) = a (a + 3)+ 1 (a + 3) = (a + 3)(a + 1)

3rd expression,

a² + 5a + 6

= a² + (3 + 2) a + 6 = a² + 3a + 2a + 6

= a (a + 3) + 2 (a + 3) = (a + 3)(a + 2)

x³ – 3x² – 10x, x³ + 6x² + 8x, x⁴ – 5x³ – 14x² = a (a + 3) + 2 (a + 3) = (a + 3)(a + 2)

∴ The required GCD is 1.

2. 1st expression

3 (a + b)³ = 3 (a + b) (a + b)(a + b)

2nd expression

6 (a + b)² = 2 x 3 x (a + b)(a + b)

3rd expression

9 (a² – b²) = 3 x 3 x (a + b)(a – b)

∴ The required GCD = 3 x (a + b) = 3 (a + b)

3. 1st expression

x³ – 3x² – 10x = x (x² – 3x – 10)

= x {x² – (5 – 2) x 10} = x{x² – 5x + 2x – 10}

= x {x(x – 5) + 2(x – 5)} = x(x – 5)(x + 2)

2nd expression

x³ + 6x² + 8x = x(x² + 6x + 8)

= x {x² + (4 + 2)x + 8}

= x {x² + 4x + 2x + 8)

= x {x (x + 4) + 2(x + 4)}

= x (x + 4)(x + 2)

3rd expression

x⁴ – 5x³ – 14x² = x² (x² – 5x – 14)

= x² (x² – (7 – 2) x 14} = x² (x² – 7x + 2x – 14}

= x² {x(x – 7) + 2(x – 7)} = x x x x (x – 7)(x + 2)

∴ The required GCD is x x x x (x + 2) = x(x + 2)

To find the L.C.M. each expression is first to be resolved into factors and the product of the factors having the highest powers in those factors will be the L.C.M.

Example 4. Find L.C.M. of the following expressions:

1. 20 a²b³c⁴, 25a³b²c², 60 abc⁵
2. 4x⁵y²z, 8xy²z³, 12yz⁴
3. xy⁴ – 8xy, x²y⁴ + 8x²y, xy⁴ – 4xy²

Solution:

1. 1st expression,

20a²b³c⁴ = 2 x 2 x 5 x a x a x b x b x b x c x c x c x c

2nd expression,

25a³b²c² = 5 x 5 x a x a x a x b x b x c x c

3rd expression,

60 abc⁵ = 2 x 2 x 3 x 5 x a x b xc x c x c x c x c

The highest power of 2 is 2, highest power of 5 is 2, highest power of 3 is 1, the highest power of a is 3, the highest power of b is 3.

The highest power of C is 5.

∴ The required L.C.M.

= 2 x 2 x 5 x 5 x 3 x a x a x a x b x b x b x c x c x c x c x c = 300 a³b³c⁵

Alternate method:

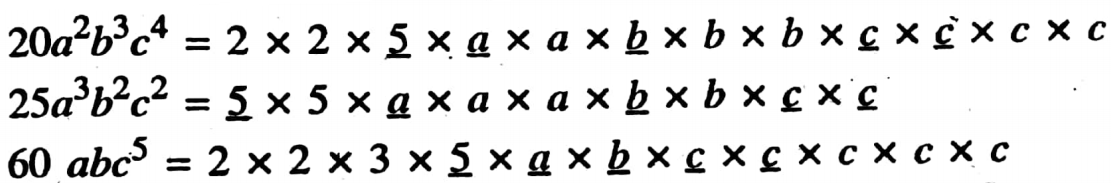
The common factor of 20a²b³c⁴, 25a³b²c² and 60abc5 is 5 x a x b x c x c = 5abc²

∴ The required LCM = 5abc² x 2 x 2 x a x b x b x c x c x 5 x a x 3 x c = 300a³b³c⁵

2. 4x⁵y²z = 2 x 2 x x x x x x x x x x x y x y x z

8xy²z³ = 2 x 2 x 2 x x x y x y x z x z x z

12yz⁴ = 2 x 2 x 3 x y x z x z x z x z

LCM = 2 x 2 x 2 x 3 x x x x x x x x x x x y x y x z x z x z = 24 x⁵y²z⁴

3. 1st expression,

xy⁴ – 8xy = xy(y³ – 8) = xy(y³ – 2³)

= xy(y – 2)(y² + y.2 +2²) = xy(y – 2)(y² + 2y + 4)

2nd expression,

x²y⁴ + 8x²y = x²y (y³ + 8)

= x²y(y³ +2³) = x²y (y + 2) (y² + y.2 + 2²)

= x.x.y(y + 2)(y² – 2y + 4)

3rd expression,

xy⁴ – 4xy² = xy²(y² – 4)

= x x y x y(y + 2)(y – 2)

The required LCM = x x x x y x y x (y + 2)(y² – 2y + 4) (y – 2)(y² + 2y + 4)

= x²y²(y + 2)(y – 2)(y² – 2y + 4)(y² + 2y + 4)

Example 5. Find the H.C.F and L.C.M. of the following algebraic expressions:

1. 8(x² – 4), 12(x³ + 8), 36(x² – 3x-10)
2. a⁴ + a²b² + b⁴, a³b + b⁴, (a² – ab)³
3. x² + y² – z² + 2xy, z² + x² – y² + 2zx, y² + z² – x² + 2yz
4. 3a² – 15a + 18, 2a2 + 2a – 24, 4a² + 36a + 80

Solution:

1. 1st expression,

8(x² – 4) = 8(x² – 2²) = 2 × 2 × 2 × (x + 2)(x − 2)

2nd expression,

12(x³ + 8)= 12 (x³ + 2³) = 12(x + 2)(x² – x·2 + 2²) = 2 × 2 × 3 × (x + 2)(x² – 2x + 4)

3rd expression,

36(x² – 3x – 10) = 36 {x² – (5 – 2)x – 10}

= 36 {x² – 5x + 2x – 10} = 36{x² – 5x + 2x – 10}

= 36 {x(x – 5) + 2(x – 5)} = 2 x 2 x 3 x 3 x (x – 5)(x + 2)

H.C.F.= 2 x 2 x (x + 2) = 4(x + 2)

L.C.M. = 2 x 2 x 2 x 3 x 3(x + 2)(x – 2)(x – 5)(x² – 2x + 4) = 72(x + 2)(x – 2)(x – 5)(x² – 2x + 4)

2. 1st expression,

a⁴ + a²b² + b⁴ = (a²)² + 2a²b² + (b²)² – a²b²

= (a² + b²) – (ab)²

= (a² + b² + ab)(a² + b² – ab)

2nd expression,

a³b + b⁴ = b(a³ + b³) = b(a + b)(a² – ab + b²)

3rd expression,

(a² – ab)³ = {a(a – b)}³ = a x a x a x(a – b)(a – b)(a – b)

∴ The required HCF = 1 and

LCM= a x a x a x b x (a + b)(a – b)(a – b)(a – b)(a² – ab + b²)(a² + ab + b²)

= a³b(a + b)(a – b)³(a² – ab + b²)(a² + ab + b²)

3. 1st expression,

x² + y² – z² + 2xy

= (x² + 2xy + y²) – z²

= (x + y)² – z² = (x + y + z) (x + y − z)

2nd expression,

z² + x² – y² + 2zx

= (z² + 2zx + x²) – y² = (z + x)² – y²

= (z + x + y) (z + x − y).

3rd expression,

y² + z² – x² + 2yz

= y² + 2yz + z² – x² = (y + z)² – x²

=(y + z + x) (y + z – x)

4. 1st expression,

3a² – 15a + 18

= 3(a² – 5a + 6) = 3{a² – (3 + 2)a + 6}

∴ HCF = (x + y + z)·

LCM = (x + y + z)(x + y = 2); (x – y + z) (y + z – x)

= 3(a² -3a – 2a + 6} = 3 {a(a – 3)- 2(a – 3)}

= 3(a – 3)(a – 2)

2nd expression,

2a² + 2a – 24

= 2 (a² + a – 12) = 2 {a² + (4 – 3)a – 12}

= 2 (a² + 4a – 3a – 12)

= 2 {a(a + 4) – 3(a + 4)}

= 2 (a + 4) (a-3)

3rd expression,

4a² + 36a + 80

= 4(a² + 9a + 20) = 4(a² + (5 + 4)a + 20)

= 4 {a² + 5a + 4a + 20)

4 {a(a + 5) + 4(a + 5)} = 2 × 2 × (a + 5) (a + 4)

HCF = 1

LCM = 2 x 2 x 3 x (a – 3)(a – 2)(a + 4)(a + 5)

= 12(a – 3)(a – 2)(a + 4)(a + 5)

Example 6. Choose the correct answer:

1. HCF of 3xy²z², 2yz²x², x²y²z is

1. xyz
2. x²y²z²
3. xyz²
4. None of these

Solution: The HCF of 3xy²z², 2yz²x^2, and x²y²z² is xyz.

∴ So the correct answer is 1. xyz

2. LCM of a²b²c², a³b²c³ and ab³c⁴ is

1. a³b³c³
2. a²b²c²
3. abc²
4. abc³

Solution: LCM is a³b³c⁴.

∴ So the correct answer is 1. a³b³c³

3. If 0 < x < 1, then HCF of x², x⁵, x is

1. x
2. x²
3. x⁵
4. None of these

Solution: Let x = \(\frac{1}{2}\)

x² = \(\frac{1}{4}\)

x⁵ = \(\frac{1}{32}\)

HCF of \(\frac{1}{32}\), \(\frac{1}{8}\) and \(\frac{1}{2}\) is \(\frac{\text { HCF of } 1,1,1}{\text { LCM of } 92,8 \text { and } \frac{1}{8}}=\frac{1}{32}=x^5\)

∴ So the correct answer is 3. x⁵

Example 7. Write ‘True’ or ‘False’:

1. If a, and b are prime numbers, then their LCM is ab.

Solution: The statement is true.

2. If a, and b are prime numbers then their HCF is 1.

Solution: The statement is true.

3. LCM of x^m and x^m+p is x^m.

Solution: \(x^{m+r}=x^m \cdot x^r\)

LCM of \(x^m and x^m \cdot x^r\) is

\(x^m \cdot x^r or x^{m+r}\)

∴ So the statement is false.

Example 8. Fill in the blanks:

1. HCF of m² + 9m + 20 and m² + 13m + 36 is _______

Solution: m² + 9m + 20 = (m + 5)(x + 4)

m² + 13m + 36= (x + 9)(x + 4)

HCF is (x + 4).

HCF of m² + 9m + 20 and m² + 13m + 36 is (x + 4).

2. LCM of (a – b) and (b – a) is _______

Solution: (a – b) or (b – a).’

LCM of (a – b) and (b – a) is (a – b) or (b – a).’

3. HCF of ax², a²x³, a⁴x is _________

Solution: ax.

HCF of ax², a²x³, a⁴x is ax.