WBBSE Solutions For Class 8 Maths Geometry Chapter 4 Properties Of Parallel Lines And Their Transversal

Geometry Chapter 4 Properties Of Parallel Lines And Their Transversal

⇒ Parallel lines: If two straight lines on the same plane do not intersect when produced in any direction, the two straight lines are said to be parallel to one.

⇔ AB and CD are parallel to each other.

⇒ Transversal: If a straight line intersects two more straight lines in different points, then the straight line is called a transversal of the lines.

Read and Learn More WBBSE Solutions For Class 8 Maths

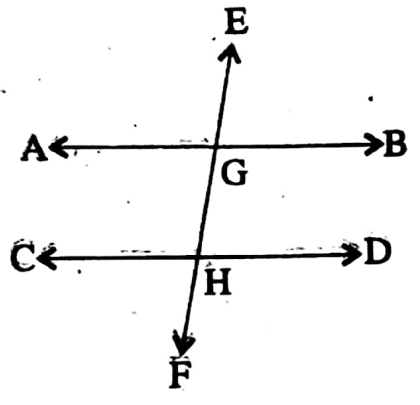
⇒ The straight line EF intersects the straight lines AB and CD at point G and H respectively.

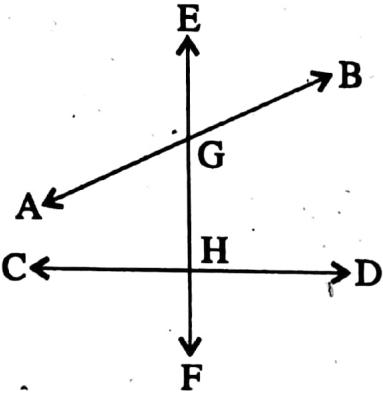
⇔ So, EF is called transversal of lines AB and CD.

⇒ Interior angles and Exterior angles: ∠1, ∠2, ∠3, and ∠4 are interior angles whereas ∠5, ∠6, ∠7, and ∠8 are exterior angles.

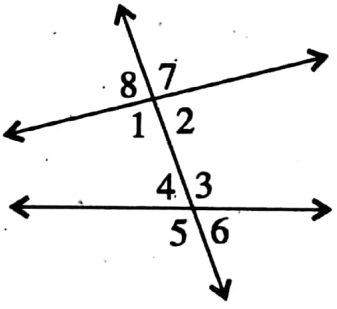
⇒ Corresponding angles: Two angles lying on the same side of the transversal are known as corresponding angles if both lie either above or below the two given lines.

⇔ There are four pairs of corresponding angles. (∠1, ∠5), (∠2, ∠6), (∠8, ∠4), and (∠7, ∠3).

⇒ Alternate angles: The pair of interior angles on the opposite side of the transversal are called alternate angles.

⇔ There are two pairs of alternate angles (∠2, ∠6) and (∠3, ∠5)

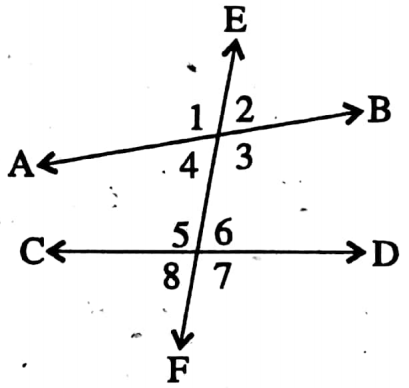
⇒ Axiom 1: If a straight line intersects two parallel lines, then the measurement of each pair of corresponding angles are equal.

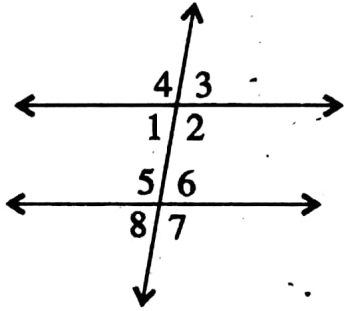
⇔ ∠4 = ∠5, ∠3 = ∠6, ∠8 = ∠1 and ∠7 = ∠2.

⇒ Axiom 2: If a straight line intersects a pair of straight lines and the measurement of one pair of corresponding angles is equal, then the two straight lines are parallel to each other.

Theorem 1: If a straight line intersects two parallel lines, then the measurement of alternate angles are equal and the sum of measurement of two interior angles in the same side of the transversal is 180° or 2 right angles.

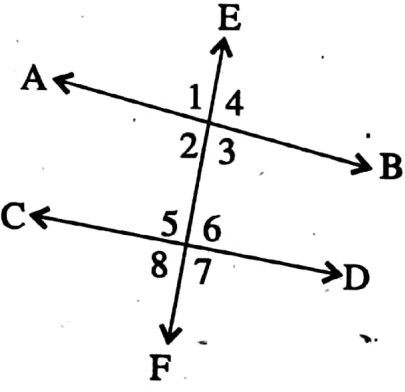
Given: Let AB and CD are two parallel lines and EF intersects AB and CD at G and H respectively.

Required to prove:

1. ∠AGH = ∠GHD
2. ∠BGH + ∠GHD = 180°

Proof:

1. AB || CD and EF is a transversal.

∴ ∠EGB = ∠GHD (Corresponding angles)

Again, ∠EGB = ∠AGH (Vertically opposite angles)

∴ ∠AGH = ∠GHD (Proved)

2. AB || CD and EF is transversal.

∴ ∠EGB = ∠GHD [Corresponding angles]

Again, GB is stands on EF

∴ ∠EGB + ∠BGH = 180°

∴ ∠GHD + ∠BGH = 180°

Theorem 2: If a straight line intersects two straight lines and if

1. Measurement of one pair of alternate angles is equal or
2. Sum of measurement of two interior angles of the same side of the transversal is two right angles, then two straight lines are parallel.

Given: Let EF intersect AB and CD at G and H respectively.

1. ∠AGH = ∠GHD (alternate angles) or
2. ∠BGH + ∠GHD = 2 right angles.

Required to Prove: AB || CD.

Proof:

1. ∠AGH = ∠EGB [Vertically opposite angles]

Again, ∠AGH = ∠GHD [Given]

∴ ∠EGB = ∠GHD and they are corresponding angles.

∴ AB || CD (Proved).

2. GB is stands on EF

∴ ∠EGB + ∠BGH = 180°

Again, ∠BGH + ∠GHD = 180° (Given)

∴ ∠EGB + ∠BGH = ∠BGH + ∠GHD

⇒ ∠EGB = ∠GHD [Subtracting ∠BGH from both sides] And this two angles are corresponding angles.

∴ AB || CD (Proved)

Geometry Chapter 3 Properties Of Parallel Lines And Their Transversal Examples

Example 1. In the adjacent find the value of x.

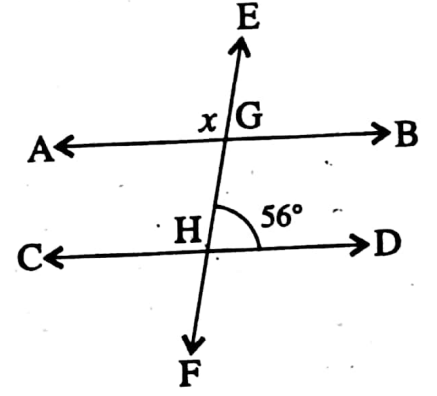
Solution: AB || CD and EF is transversal.

∴ ∠EGB = ∠GHD [Corresponding angles] = 56°

∠AGE + ∠EGB = 180° [As GE stands on AB]

x + 56° = 180°

⇒ x = 180° – 56°

⇒ x = 124°

∴ The value of the x = 124°

Example 2. In the adjacent find the value of y.

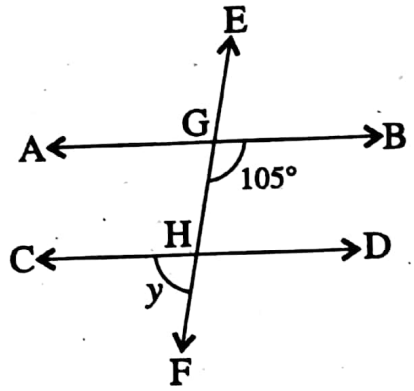
Solution: AB || CD and EF is transversal.

∴ ∠DHF = ∠BGH (Corresponding angles) = 105°

∠CHF + ∠DHF = 180°

y + 105° = 180°

⇒ y = 180° – 105°

⇒ y = 75°

∴ The value of the y = 75°

Example 3. Examining the measurement of the angles given below conclude logically AB and CD are parallel.

Solution:

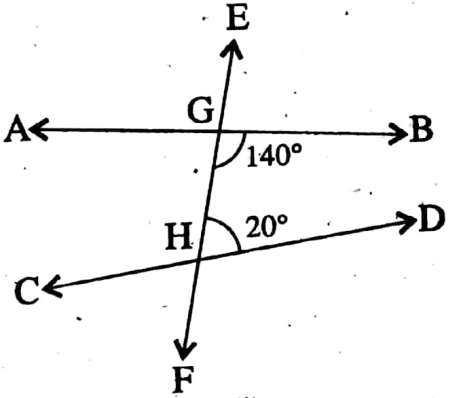
1. ∠BGH + ∠GHD = 140° + 20° = 160° 180°

∴ AB and CD are not parallel lines to each other.

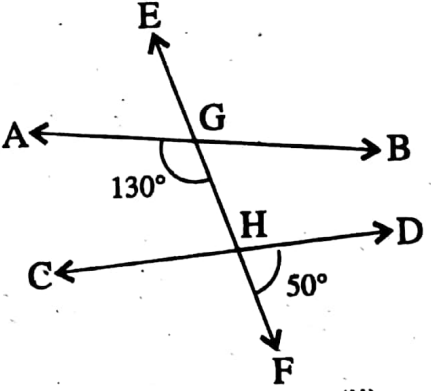
2. ∠BGH = 180°- ∠AGH = 180° – 130° = 50°

Again, ∠DHF = 50°

∴ ∠BGH = ∠DHF and these angles are corresponding angles.

∴ AB || CD

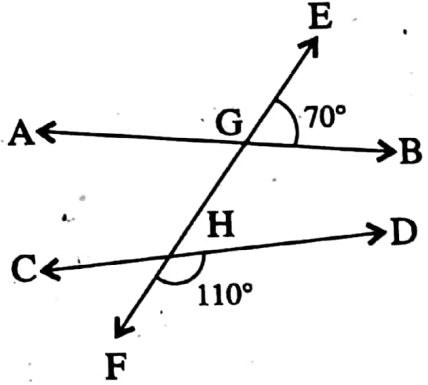
3. ∠BGH = 180°- ∠EGB = 180°-70° = 110°

Again, ∠DHF = 110°

∴ ∠BGH = ∠DHF and these angles are corresponding angles.

∴ AB || CD.

⇔ AB and CD are parallel.

Example 4. In the adjacent AB || CD, ∠RCD = 30°, ∠PAB = 50°, ∠PAC = 140°. Find the measurement of all the angles of ΔAQC.

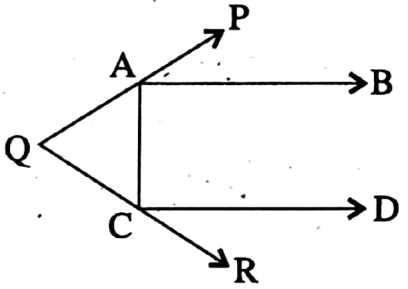
Solution:

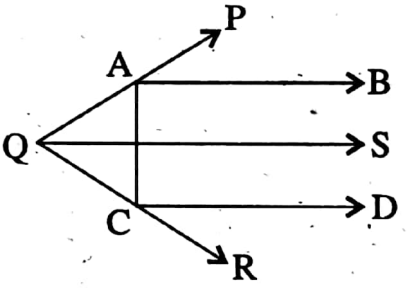
I drew QS through Q which is parallel to AB.

As AB || CD and AB || QS

∴ AB || QS || CD

AB || QS and PQ is transversal.

∴ ∠PQS = ∠PAB [Corresponding angles] = 50°

QS || CD and QR is transversal.

∴ ∠RQS = ∠RCD [Corresponding angles]= 30°

∠AQC = ∠PQS + ∠RQS = 50° + 30° = 80°

∠QAC + ∠PAC = 180°

∠QAC + 140° = 180°

⇒ ∠QAC = 180°

⇒ ∠QAC = 180° – 140° = 40°

In ΔAQC, ∠AQC = 80°, ∠QAC = 40°

∴ ∠ACQ = 180° – (80° + 40°) [In ΔAQC, ∠QAC + ∠AQC + ∠ACQ = 180°]

= 180° – 120°

∴ The angle of triangle ΔAQC = 60°

Example 5. In parallelogram PQRS, if ∠P = 90°, then find the values of other three angles.

Solution: In parallelogram PQRS;

SP || RQ and PQ is transversal:

∴ ∠P + ∠Q = 180°

∴ 90° + ∠Q = 180°

⇒ Q = 180° – 90° = 90°

Again, SR || PQ and RQ is transversal.

∴ ∠Q + ∠R = 180°

90° + ∠R = 180°

⇒ ∠R = 180° – 90° = 90°

Similarly ∠S = 90°

Example 6. In the adjacent AB || CD and ∠EGB = 50°. Find the values of ∠AGE, ∠AGH, ∠CHF, and ∠DHF.

Solution: ∠AGE + ∠EGB = 180°

∠AGE + 50° = 180°

⇒ ∠AGE = 180° – 50° = 130°

⇒  ∠AGH = ∠EGB [Vertically opposite angles] = 50°

AB || CD and EF is transversal.

∴ ∠GHD = ∠AGH [Alternate angles] = 50°

∠CHF = ∠GHD = 50°

∠CHF + ∠DHF = 180°

50° + ∠DHF = 180°

∴ ∠DHF = 180° – 50° = 130°

Example 7. If the adjacent, PQ || RS; if ∠BAQ = 3∠ABS, then find the value of ∠RBN.

Solution: AB || RS and MN is transversal.

∴ ∠BAQ + ∠ABS = 180°

3∠ABS + ∠ABS = 180°

⇒ 4∠ABS = 180°

⇒ ∠ABS = \(\frac{180^{\circ}}{4}=45^{\circ}\) = 45°

∠RBN = ∠ABS = 45°.

The value of ∠RBN 45°.

Example 8. O is any point inside two parallel lines AB and CD. OP and OQ are two perpendiculars on AB and CD respectively. Prove that P, O, and Q are collinear.

Solution:

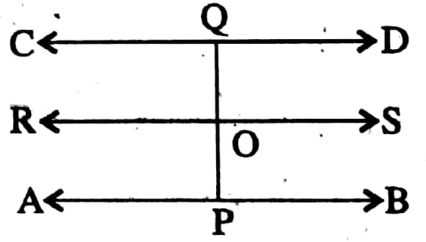
Through O the straight line RS is drawn parallel to AB.

AB || CD and AB || RS.

∴ AB || CD || RS

OP ⊥ AB.

∴ ∠OPB = 90°

OQ ⊥ CD.

∴ ∠OQD = 90°

AB || RS and OP is transversal.

∴ ∠OPB + ∠POS = 180°

90° + ∠POS = 180°

⇒ ∠POS = 180°- 90° = 90°

CD || RS and OQ is transversal.

∠OQD + ∠QOS = 180°

90° + ∠QOS = 180°

⇒ ∠QOS = 180° – 90° = 90°

∠POQ = ∠QOS + ∠POS= 90° + 90° = 180°

∴ OP and OQ lies on the same straight line.

∴ P, O, and Q are collinear.

Example 9. If the sides of an angles are respectively parallel to the sides of another angle, then the angles are either equal or supplementary.

Solution: Given Let in angles ∠ABC and ∠DEF, AB || DE and BC || EF, BC, and DE intersect at G.

Required to Prove:

1. ∠ABC = ∠DEF [from (1)]
2. ∠ABC and ∠DEF supplementary i.e. ∠ABC + ∠DEF = 180° [From (2)]

Proof:

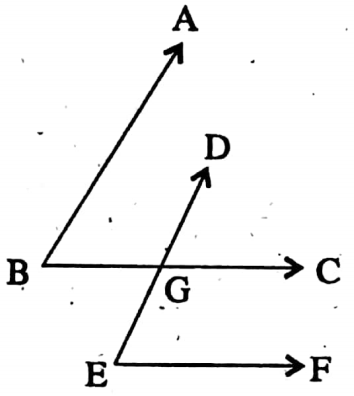
From (1) AB || DE and BC is transversal.

∴ ∠ABC = ∠DGC [Corresponding angles]

Again, BC || EF and DE is transversal.

∴ ∠DGC = ∠DEF [Corresponding angles]

As ∠ABC = ∠DGC and ∠DGC = ∠DEF

∴ ∠ABC = ∠DEF (Proved).

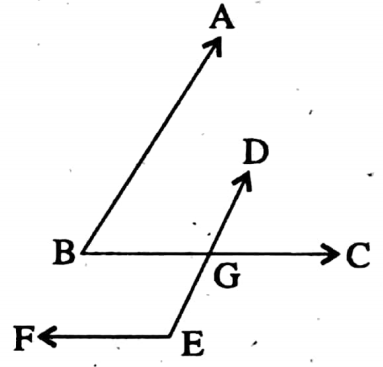
From (2) BC || EF and DE is transversal.

∴ ∠DGB = ∠DEF [Corresponding angles]

Again, AB || DE and BC is transversal.

∴∠ABC + ∠DGB = 180°

∴ ∠ABC + ∠DEF = 180°

∴ ∠ABC and ∠DEF are supplementary angles. (Proved)

Example 10. Prove that straight lines perpendicular to the same straight line are parallel to one another.

Solution: Let PQ and RS are both perpendicular to AB.

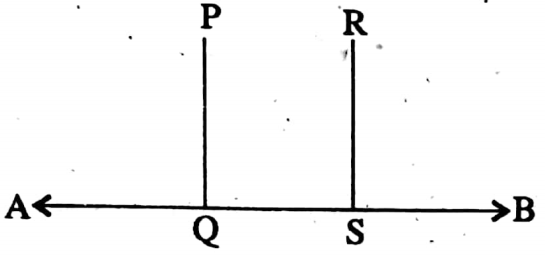
Required to Prove: PQ || RS

Proof: PQ ⊥ AB

∴ ∠PQB = 90°

∴ RS ⊥ AB

∴ ∠RSB = 90°

∴ ∠PQB = ∠RSB and these are corresponding angles.

∴ PQ || RS (Proved).

Example 11. Choose the correct answer:

1. In the adjacent if AB || CD, then the value of x is,

1. 68°
2. 22°
3. 112°
4. 34°

Solution: AB || CD and EF is transversal.

∴ ∠EGB = ∠GHD [Corresponding angles] = 68°

The ray GE is stands on line AB

∴ ∠AGE + ∠EGB = 180°

∠AGE + 68° = 180°

⇒ ∠AGE = 180° – 68°

⇒ x° = 112°

∴ So the correct answer is 3. 112°

The value of x is 112°

2. In the adjacent if AB || CD, then value of x is

1. 50
2. 40
3. 60
4. 70

Solution: AB || CD and EF is transvesal.

∴ ∠GHD = ∠EGB [Corresponding angles] = (2x – 50)°

∠GHD + ∠FHD = 180°

2x – 50 + x + 80 = 180

3x + 30 = 180

3x = 150

⇒ x = \(\frac{150}{3}\) = 50

∴ So the correct answer is 1. 50

Value of x is 50.

3. In the adjacent AB || CD, if ∠EGB = 50°, then the value of x is

1. 130°
2. 40°
3. 50°
4. 60°

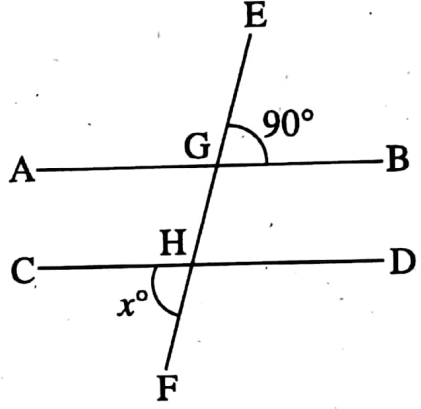
Solution: ∠GHD = ∠EGB = 50°

∠CHF = ∠GHD [Vertically opposite angle] = 50°

∴ So the correct answer is 3. 50°

The value of x is 50°

Example 12. Write ‘True’ or ‘False’:

1. In the adjacent if ∠3 = 120° and ∠8 = 60°, then AB || CD.

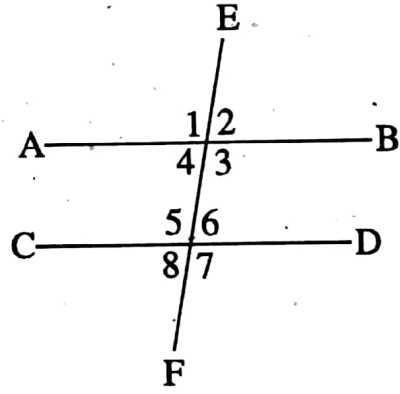
Solution: ∠6 = ∠8 = 60°

∠3 + ∠6 = 120° + 60° = 180°

∴ AB || CD

∴ So the statement is true.

2. In the adjacent if ∠EGB = 75° and ∠DHF = 95°, then AB || CD.

Solution: ∠AGH = ∠EGB [Vertically opposite angles] = 75°

∴ ∠GHC = ∠DHF = 95°

∠AGH + ∠GHC = 75° + 95° = 170°

∴ AB and CD are not parallel to each other.

∴ So the statement is false.

Example 13. Fill in the blanks:

1. In the adjacent, AB || CD and GP is the bisector of ∠AGH; if ∠AGP= 40°, then the value of ∠FHD is ________

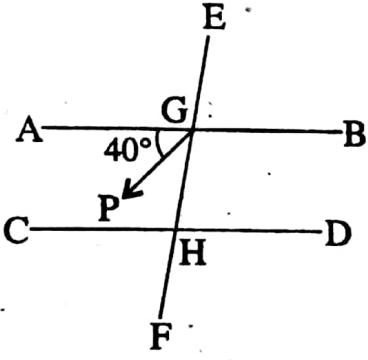
Solution: ∠AGH = 2 ∠AGP = 2 x 40° = 80°

AB || CD

∴ ∠AGH + ∠GHC = 180°

80° + ∠GHC 180°

⇒ ∠GHC = 100°

∠FHD = ∠GHC = 100°

The value of ∠FHD is 100°.

2. Straight lines perpendicular to the same straight line are ________

Solution:

CD ⊥ AB and EF ⊥ AB

∴ ∠DCB + ∠FEC = 90° = 90° + 90° = 180°

∴ DC || FE

Answer: Parallel.

Straight lines perpendicular to the same straight line are  Parallel.