Geometry Chapter 5 Relation Between Two Sides Of A Triangle And Their Opposite Angles
⇒ Axiom: Two triangles are congruent if the length of two sides and the measurement of the included angle of one triangle are equal to the length of two sides and the measurement of the included angle of the other triangle. (SAS)
Theorem 1. Angles opposite to equal sides of an isosceles triangle are equal in measure.
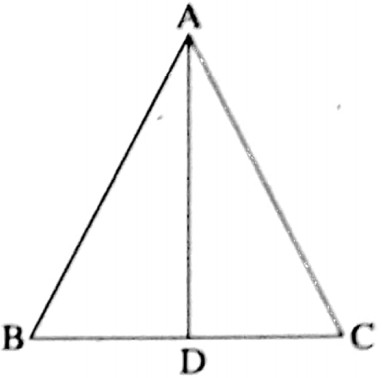
Given: ABC is a triangle where AB = AC.
Required to prove: In ΔABC, the measurement of angles opposite to two equal sides AB and AC are equal.
i.e. ∠ACB = ∠ABC.
Read and Learn More WBBSE Solutions For Class 8 Maths
Construction: I draw the bisector AD of ∠BAC which intersects BC at D.
Proof: In ΔABD and ΔACD,
AB = AC (given)
∠BAD = ∠CAD [by construction]
and AD = AD [Common side]
∴ ΔABD ≅ ΔACD [by SAS congruence rule]
∴ ∠ABD = ∠ACD [Corresponding angles of congruent triangles]
Hence, ∠ABC = ∠ACB (Proved).
| WBBSE Class 8 English Functional Grammar | WBBSE Class 8 English Reading Skills |
| WBBSE Solutions For Class 8 English | WBBSE Solutions For Class 8 Maths |
Theorem 2.
- Two triangles are congruent if measurement of any pair of angles and length of one pair of corresponding sides are equal to the other triangle. (AAS)
- If length of three sides of one triangle is equal to the length of three sides of another triangle then the two triangles are congruent. (SSS)
- If in two right angled triangles the length of hypotenuse and length of one side of one triangle are equal to the length of the hypotenuse and the length of one side of the other triangle, then the two triangles are congruent. (RHS)
Theorem 3. The length of opposite sides of two angles equal in measurement of a triangle are equal.

Given: In ΔABC, ∠ABC = ∠ACB.
Required to prove: AB = AC
Construction: I draw the bisector AD of ∠BAC which intersect BC at D.
Proof: In ΔABD and ΔACD,
∠BAD = ∠CAD [AD is a bisector of ∠BAC]
AD = AD [Common side]
and ∠ABD = ∠ACD (Given)
∴ ΔABD ≅ ΔACD [By AAS congruence rule]
∴ AB = AC [Corresponding sides of congruent triangles) (Proved)
Geometry Chapter 5 Relation Between Two Sides Of A Triangle And Their Opposite Angles Examples
Example 1. If the measurement of an angle of an isosceles triangle is 105°, then find the measurement of other two angles.
Solution: The sum of two acute angles is (180° – 105°) or 75°.

Let ∠A = 105° and AB = AC
∴ ∠B = ∠C = \(\frac{180^{\circ}-105^{\circ}}{2}=\frac{75^{\circ}}{2}=37 \cdot 5^{\circ}\)
The measurement of other two angles \(\frac{180^{\circ}-105^{\circ}}{2}=\frac{75^{\circ}}{2}=37 \cdot 5^{\circ}\)
Example 2. In an isosceles triangle one angle of the base is 55°, then find the measurement of vertical angle.
Solution: In an isosceles triangle one angle of the base is 55°.
∴ The other angle of base is 55°.
Then the vertical angle is 180° – (55° + 55°) = 180° – 110° = 70°
Example 3. In an isosceles triangle, the vertical angle is three times of each angle of the base. Find the measurement of the supplementary angle of the vertical angle.
Solution: Let measurement of each angle of the base is x°.
∴ The measurement of vertical angle is 3x°.
Sum of the three angles of a triangle is 180°.
∴ 3x + x + x° = 180°
⇒ 5x° = 180°
⇒ x = \(\frac{180^{\circ}}{5}=36^{\circ}\)
⇒ The vertical angle is (3 x 36°) or 108°.
The supplementary angle of verticle angle is (180° – 108°) or 72°.
Example 4. In the adjacent, in ΔABC, AB = AC, If ∠A + ∠B = 115°, find the measurement of ∠A.
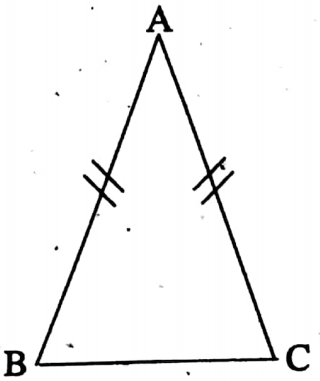
Solution: In ΔABC, ∠A + ∠B + ∠C = 180°
115° + ∠C = 180°
⇒ ∠C = 180° – 115° = 65°
As AB = AC
∴ ∠B = ∠C = 65°
∠A = 115° – 65° = 50°
The measurement of ∠A = 50°
Example 5. In ΔABC, AB = AC; The bisector of ∠ABC intersects AC at D. If ∠A = 56°, then find the value of ∠ABD.
Solution:
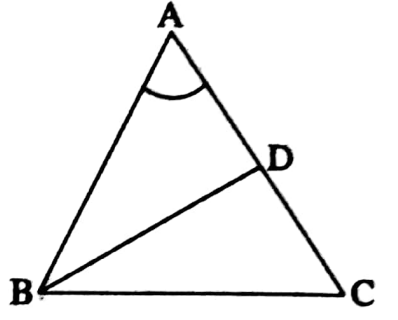
In ΔABC,
AB = AC
∴ ∠ABC = ∠ACB
∠BAC = 56°
In ΔABC, ∠BAC+ ∠ABC + ∠ACB = 180°
56° + ∠ABC + ∠ABC = 180°
⇒ 2∠ABC = 180° – 56° = 124°
⇒ ∠ABC = \(\frac{124^{\circ}}{2}=62^{\circ}\)
As BD is the bisector of ∠ABC.
∴ ∠ABD = \(\frac{1}{2}\)∠ABC = \(\frac{1}{2}\)∠ABC = \(\frac{1}{2}\) x 62° = 31°
The value of ∠ABD = 31°
Example 6. Two line segments AB and CD bisect each other at O; If AC = 4 cm, then find the length of BD.
Solution:
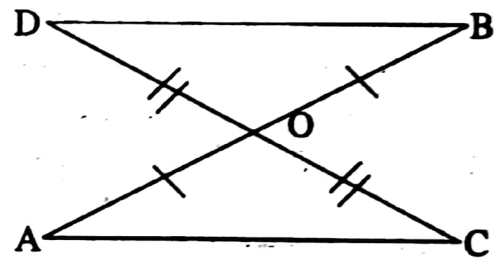
In ΔAOC and ΔBOD,
OA = OB, OC = OD and ∠AOC = ∠BOD [Vertically opposite angle]
ΔAOC ≅ ΔBOD [by SAS congruency]
∴ AC = BD
4 cm = BD
∴ The length of BD is 4 cm.
Example 7. In ΔABC, AB = AC; BC is extended to D such that AC = CD; if ∠ABC = 70°, then find the value of ∠BAD.
Solution:
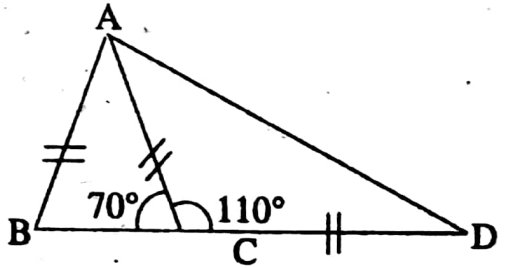
In ΔABC, AB = AC
∴ ∠ACB = ∠ABC = 70°
Again, ∠ACB + ∠ACD = 180°
70° + ∠ACD = 180°
⇒ ∠ACD = 180° – 70° = 110°
In ΔACD, AC = CD
∴ ∠DAC = ∠ADC
∠ACD + ∠ADC + ∠DAC = 180°
110° + ∠ADC + ∠ADC= 180°
2∠ADC = 180° – 110° = 70°
⇒ ∠ADC = \(\frac{70^{\circ}}{2}=35^{\circ}\)
In ΔABD, ∠ABD + ∠ADB + ∠BAD = 180°
i.e. ∠ABC + ∠ADC + ∠BAD = 180°
70° +35° + ∠BAD = 180°
⇒ ∠BAD = 180°- 105° = 75°
The value of ∠BAD = 75°
Example 8. Prove that the lengths of the medians are equal in length in an equilateral triangle.
Solution:
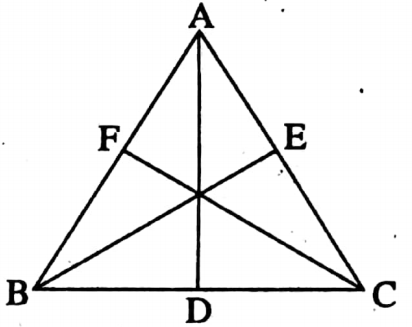
Given, In ΔABC,
AB = BC = AC
Let AD, BE and CF are three medians of ΔABC.
Required to Prove: AD = BE = CF
Proof: AB = AC
⇒ \(\frac{1}{2}\)AB – \(\frac{1}{2}\)AC
∴ FB = EC [F and E are the midpoints of AB and AC respectively]
In ΔFBC and ΔEBC,
FB = EC
∠FBC = ∠ECB [As in ΔABC, AB = AC ∴ ∠ABC = ∠ACB] and BC = BC [Common side]
∴ ΔFBC ≅ ΔEBC [By SAS congruency]
∴ CF = BE (Corresponding sides of congruent triangles.]
Similarly, it can be proved from ΔABE and ΔADB that BE = AD
∴ AD = BE = CF (Proved)
Example 9. In trapezium ABCD, AD || BC and ∠ABC = ∠BCD. Prove that ABCD is an isosceles trapezium.
Solution: In trapezium ABCD, AD || BC and ∠ABC = ∠BCD. (Given)
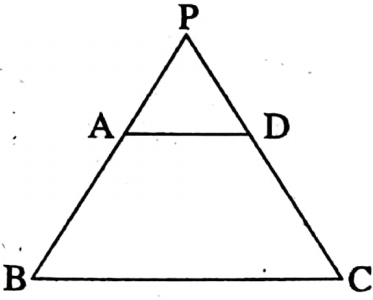
Required to Prove: ABCD is an isosceles trapezium.
Construction: BA and CD are extended which meets at a point P.
Proof: In ΔPBC, ∠PBC = ∠PCB (given)
∴ PB = PC
AD || BC and AB is transversal.
∴ ∠PAD = ∠ABC [Corresponding angles]
Again, AD || BC and AC is transversal.
∴ ∠PDA = ∠BCD [Corresponding angles]
As ∠ABC = ∠BCD (given)
∴ ∠PAD = ∠PDA
In ΔPAD, ∠PAD = ∠PDA
∴ PA = PD
PB – PA = PC – PD
∴ AB = DC
∴ ABCD is an isosceles trapezium. (Proved)
Example 10. AB is the hypotenuse of the isosceles right angled triangle ABC. AD is the bisector of ∠BAC and AD intersects. BC at D. Prove that AC + CD = AB.
Solution: In right angled isosceles triangle ABC, AB is the hypotenuse.
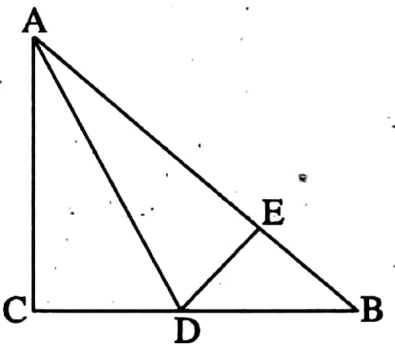
AD is the bisector of ∠BAC and AD intersects BC at D. (Given)
Required to Prove: AC + CD = AB.
Construction: Through D I draw DE which is perpendicular on AB.
Proof: In ΔACD and ΔADE,
∠CAD = ∠EAD [as AD is the bisector of ∠BAC]
∠ACD = ∠AED = 90° [DE ⊥ AB] and AD is common side.
∴ ΔACD ≅ ΔADE [by AAS congruency]
∴ AC = AE [Corresponding sides of congruent triangles]
and CD = DE [Corresponding sides]
In ΔABC, ∠ACB = 90° and AC = BC.
∴ ∠BAC = ∠ABC = \(\frac{90^{\circ}}{2}=45^{\circ}\)
In ΔBDE, ∠BED = 90°, ∠B = 45°
∴ ∠BDE = 180° – 90° – 45° = 45°
∴ ∠BDE = ∠B
∴ BE = DE
∴ Again CD = DE.
∴ DE = CD = BE
AC + CD = AE + BE = AB
AB is the hypotenuse of the isosceles right-angled triangle ABC Hence (Proved).
Example 11. Two isosceles triangle ABC and DBC are situated on the opposite side of BC. Prove that AD bisects BC perpendicularly.
Solution: Two isoscles triangle ABC and DBC are situated on the opposite side of BC.
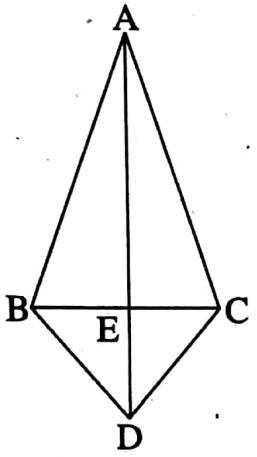
AD intersect BC at E. (Given)
Required to Prove: AD ⊥ BC and BF = CE
Proof: In ΔABD and ΔACD,
AB = AC (given)
BD = CD (given) and AD is common side.
∴ ΔACD ≅ ΔABD [By SAS congruence law]
∴ ∠BAD = ∠CAD [Corresponding angles of congruent triangles]
i.e. ∠BAE = ∠CAE
In ΔABE and ΔACE,
AB = AC, ∠BAE = ∠CAE and AE is common side.
∴ ΔABE ≅ ΔACE [By SAS congruency]
∴ BE = CE [Corresponding sides] (Proved)
and ∠AEB = ∠AEC
Again ∠AEB + ∠AEC = 180° ∠AEB + ∠AEB = 180° = 2∠AEB = 180°
⇒ ∠AEB = 90°.
∴ AE ⊥ BC i.e. AD ⊥ BC (Proved)
Example 12. Choose the correct answer:
1. In the adjacent, in ΔABC, which relation is correct?
- AB = BC
- AB = AC
- AC = BC
- AC ≠ BC
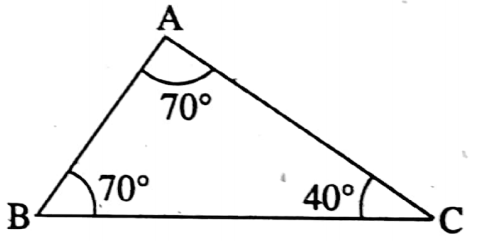
Solution: In ΔABC, ∠BAC = ∠ABC = 70°
∴ AC = BC [If the two angles of a triangle are equal then their opposite sides are equal]
∴ So the correct answer is 3. AC = BC
2. In ΔABC, AB = AC; If ∠BAC 70°, then the value of ∠ACB is
- 70°
- 110°
- 35°
- 55°
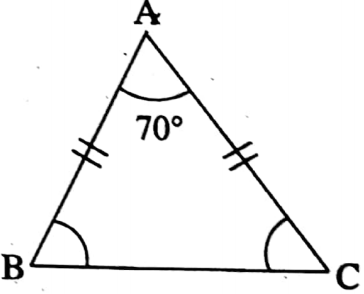
Solution: In ΔABC, AB = AC
∴ ∠ACB = ∠ABC.
Again, ∠BAC+ ∠ABC + ∠ACB = 180°
70° + ∠ACB + ∠ACB = 180°
⇒ 2∠ACB = 180°- 70° = 110°
⇒ ∠ACB = \(\frac{110^{\circ}}{2}\) = 55°
∴ So the correct answer is 4. 55°
The value of ∠ACB is 4. 55°.
3. In the adjacent, in ΔABC, AB = AC and DE || BC; If ∠AED = 50°, then the value of ∠ABC is
- 50°
- 80°
- 100°
- 70°
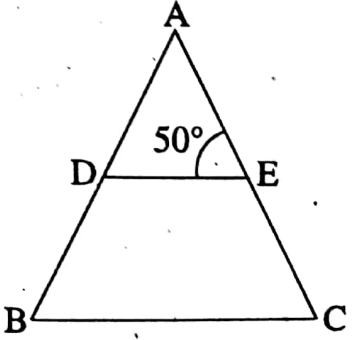
Solution: DE || BC and AC is transversal.
∴ ∠ACB = ∠AED [Corresponding angles] = 50°
In ΔABC, AB = AC
∴ ∠ACB = ∠ABC 50° = ∠ABC.
∴ So the correct answer is 1. 50°
The value of ∠ABC is 50°
Example 13. Write ‘True’ or ‘False’:
1. In an isosceles obtuse-angled triangle the measurement of an acute angle is 1/4 of measurement of the obtuse angle. The value of the acute angle is 20°.
Solution: Let value of each acute angle is x°.
∴ The value of obtuse angle is 4x°.
4x° + x° + x° = 180°
⇒ 6x° = 180°
⇒ x° = \(\frac{180^{\circ}}{6}=30^{\circ}\)
The measurement of each acute angle is 30°.
∴ So the statement is false.
2. In the adjacent, in ΔABC, AB = AC and ∠ACD = 100°. The value of ∠ABE becomes 100°.
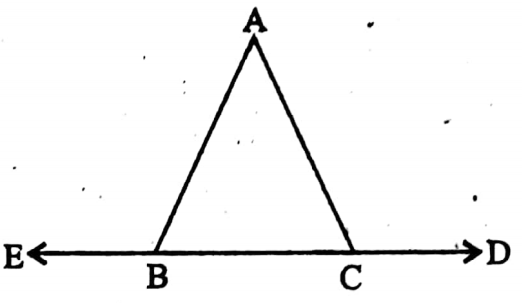
Solution: AC is stands on line ED.
∴ ∠ACD + ∠ACB = 180°
100° + ∠ACB = 180°
⇒ ∠ACB = 80°
In ΔABC, AB = AC
∴ ∠ABC = ∠ACB = 80°
As AB is stands on ED.
∴ ∠ABC + ∠ABE = 180°
80° + ∠ABE = 180°
⇒ ∠ABE = 180° – 80° = 100°
The value of ∠ABE becomes 100°
∴ So the statement is true.
Example 14. Fill in the blanks:
1. The measurement of each acute angle of an isoceles right-angled triangle is _______
Solution:
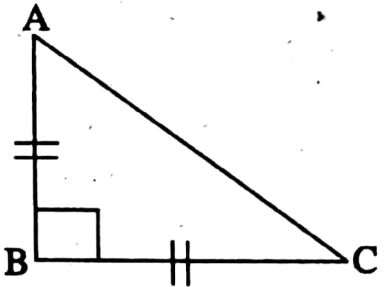
∠ABC = 90° and AB = BC
∴ ∠A = ∠C
∠A + ∠B + ∠C = 180°
∠A + 90° + ∠A = 180°
⇒ 2∠A = 90°
⇒ A = 45°
∴ The measurements of each acute angle is 45°.
2. The measurement of each angle of an equilateral triangle is _______
Solution: Three sides are equal.
Hence three angles are equal.
∴ Each angle is = \(\frac{180^{\circ}}{3}=60^{\circ}\)
