WBBSE Solutions For Class 8 Maths Geometry Chapter 6 Verification Of The Relation Between The Angles And Sides Of A Triangle

Geometry Chapter 6 Verification Of The Relation Between The Angles And Sides Of A Triangle

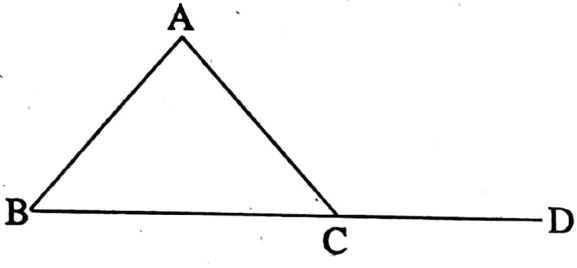
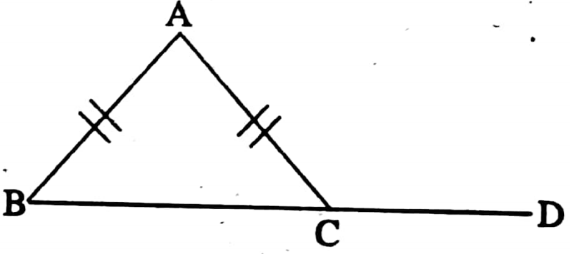
⇒ Exterior angle: The angle formed by extended of one side of an angle through vertex toward opposite direction is called the exterior angle of the given angle.

The exterior angle of ∠ABC is ∠CBD and the exterior angle of ∠CBD is ∠ABC.

ΔABC the BC is extended to D.

Read and Learn More WBBSE Solutions For Class 8 Maths

∠ACD is called exterior angle ∠BAC and ∠ABC are interior opposite angles.

Geometry Chapter 6 Verification Of The Relation Between The Angles And Sides Of A Triangle Theorems

Theorem 1.

⇒ If one side of a triangle is produced then one exterior angle is formed, the measurement of this exterior angle is sum of the measurement of two interior opposite angles.

Given: ABC is a triangle and BC is produced to D. As a result one exterior angle ∠ACD and two interior opposite angles ∠BAC and ∠ABC are produced.

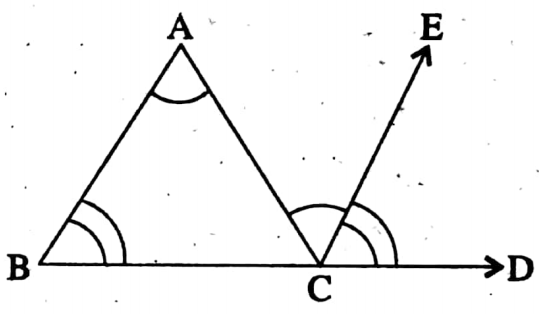
Required to prove: ∠ACD = ∠BAC + ∠ABC.

Construction: CE is drawn parallel to AB.

BA | | CE (by construction) and AC is, transversal.

∴ ∠ACE = ∠BAC [alternate angles]

Again BA || CA and BD is transversal.

∴ ∠ECD = ∠ABC [Corresponding angles]

∠ACE + ∠ECD = ∠BAC + ∠ABC i.e. ∠ACD = ∠BAC + ∠ABC (Proved)

Theorem 2.

⇒ The sum of the measurement of three angles of a triangle is two right angles.

Given: ΔABC is any triangle.

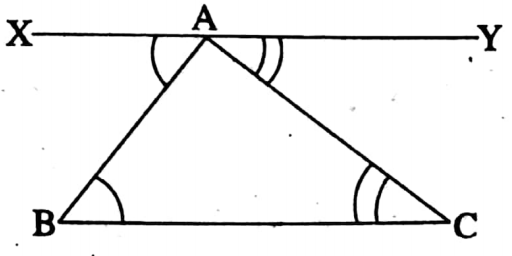
Required to prove: The sum of measurement of three angles of ΔABC is 2 right angles.

i.e. ∠BAC+ ∠ABC + ∠ACB = 180°

Construction: A straight line XY is drawn through A, parallel to BC.

Proof: XY || BC [By construction] and AB is transversal

∴ ∠ABC = ∠XAB [alternate angles]

Again, XY || BC and AC is transversal.

∴ ∠ACB = ∠CAY [alternate angles]

∠ABC +∠ACB = ∠XAB + ∠CAY

∴ ∠ABC + ∠ACB + ∠BAC = ∠XAB + ∠BAC + ∠CAY [By adding BAC on both sides]

ie. ∠BAC + ∠ABC + ∠ACB = ∠XAY

∴ ∠BAC+ ∠ABC + ∠ACB = 180° [one straight angle] (Proved)

Theorem 3.

⇒ If two sides of a triangle are unequal in length the measurement of the angle opposite to the greater side is greater than the measurement of the angle opposite to the smaller side.

Given: In ΔABC, AB > AC.

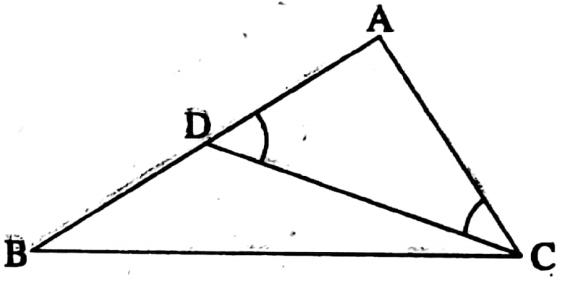
Required to prove: ∠ACB > ∠ABC

Construction: I cut off the line segment AD from the side AB equal of the side AC.

I join two point C and D.

Proof: In ΔADC, AD = AC [By construction]

∴ ∠ADC = ∠ACD

In ΔBCD, the exterior ∠ADC = ∠DBC +∠DCB

∴ ∠ADC > ∠DBC

∴ ∠ACD > ∠DBC ∠ACD + ∠DCB > ∠DBC

i.e. ∠ACB > ∠ABC (Proved).

Theorem 4.

⇒ If the measurement of two angles of a triangle are unequal,, then the length of opposite side of the greater angle is greater than the length of the opposite side of the smaller angle.

Given: In ΔABC, ∠ABC > ∠ACB.

Required to prove: AC > AB

Prove: If AC not equal to greater than AB then either

1. AC = AB or
2. AC = AB

If AC < AB then ∠ABC < ∠ACB. It cannot be true.

Because it is given ∠ABC > ∠ACB.

Again, if AC = AB then ∠ABC= ∠ACB

It cannot be true because it is given ∠ABC > ∠ACB.

∴ AC > AB (Proved)

Geometry Chapter 6 Verification Of The Relation Between The Angles And Sides Of A Triangle Examples

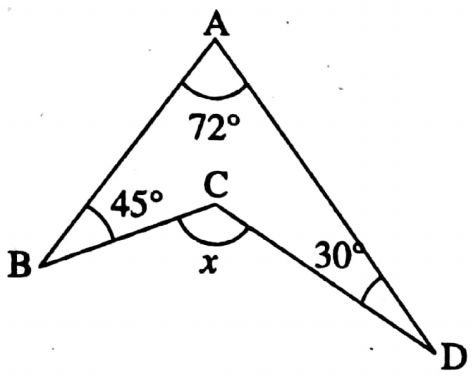
Example 1. In the adjacent, find the value of x.

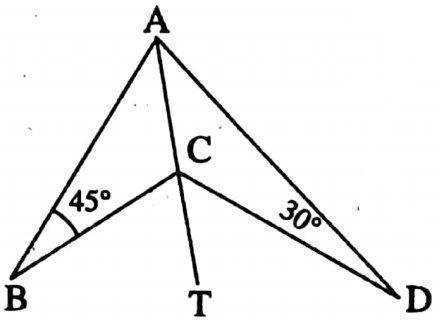
Solution: I joined A, C and AC is produced to T.

In ΔABC,

Exterior ∠BCT = ∠BAC+ ∠ABC

In ΔACD,

Exterior ∠BCT = ∠BAC + ∠ABC

In ΔACD,

Exterior ∠DCT = ∠DAC + ∠ADC

∠BCT + ∠DCT = (∠BAC+ ∠DAC) + ∠ABC + ∠ADC

i.e. ∠BCD = ∠BAD + ∠ABC + ∠ADC

x = 72° + 45° + 30°

⇒ x = 147°.

The value of x = 147°.

Example 2. In the adjacent find the value of ∠A + ∠B + ∠C+ ∠D + ∠E + ∠F.

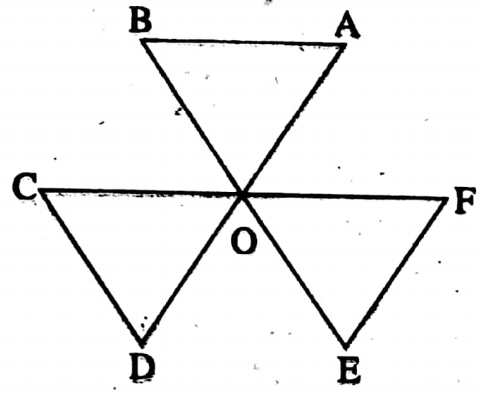
Solution: (∠A + ∠B) + (∠C + ∠D) + (∠E + ∠F)

= ∠BOD + ∠DOF + ∠FOB = -360°

The value of ∠A + ∠B + ∠C+ ∠D + ∠E + ∠F is -360°

Example 3. In ΔABC, BC is produced to D. If ∠ACD = 126° and ∠B = \(\frac{3}{4}\) ∠A then find the value of ∠A.

Solution:

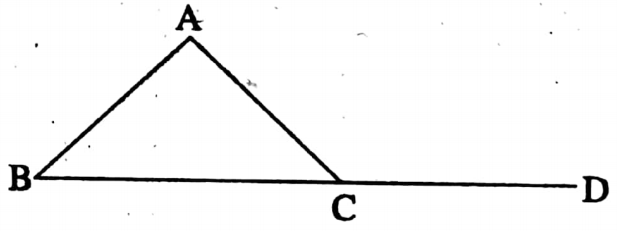
In ΔABC

∠A + ∠B = exterior ∠ACD

∠A + \(\frac{3}{4}\)∠A = 126°

⇒ \(\frac{7 \angle A}{4}\) = 126°

⇒ ∠A = \(\frac{4}{7}\) x 126° = 4 x 18° = 72°

The value of ∠A = 72°

Example 4. If the largest angle of a triangle is an acute angle then find the limit of that angle.

Solution: In ΔABC, ∠A is largest.

As ∠A is acute angle.

∴ ∠A < 90°.

Again ∠A is largest.

∴ ∠A > ∠B and ∠A > ∠C

∴ ∠A + ∠A > ∠B + ∠C

⇒ 2∠A > ∠B + ∠C

⇒ 2∠A + ∠A > ∠A + ∠B + ∠C

⇒ 3∠A > 180°

⇒ ∠A > \(\frac{180^{\circ}}{3}\)

⇒ ∠A > 60°

⇒ 60° < ∠A

∴ 60° < ∠A < 90°.

The limit of that angle  60° < ∠A < 90°.

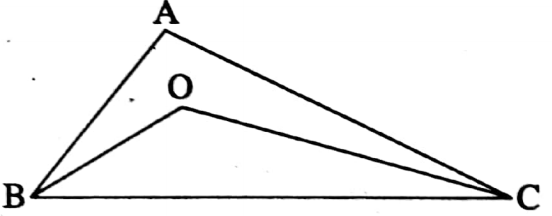
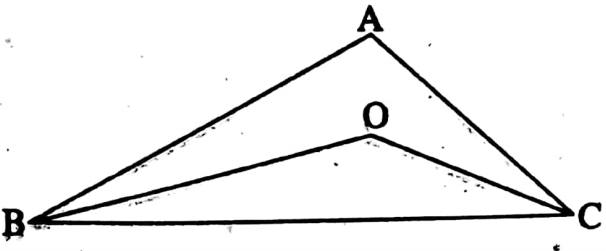
Example 5. If O is an interior point of AABC, then find the relation between ∠BOC and ∠BAC.

Solution:

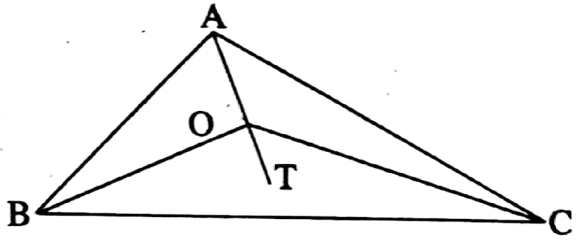
I join A, O, and AO is extended to T.

In ΔAOB, the exterior ∠BOT = ∠BAO + ∠ABO

∴ ∠BOT > ∠BAO

Similarly, In ΔAOC, ∠COT > ∠CAO

∴ ∠BOT + ∠COT > ∠BAO + ∠CAO

i.e. ∠BOC > ∠BAC.

This is the relation.

The relation between ∠BOC and ∠BAC is  ∠BOC > ∠BAC.

Example 6. Find the sum of measurement of all angles of a quadrilateral.

Solution:

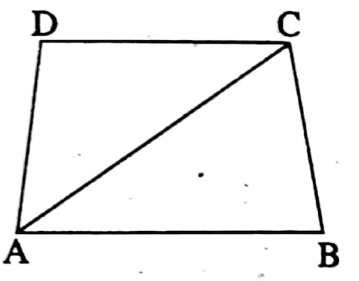
In quadrilateral ABCD, I join A and C.

In ΔABC,

∠BAC + ∠ABC + ∠ACB = 180°

In ΔADC, ∠DAC+ ∠ADC + ∠ACD = 180°

(∠BAC + ∠DAC) + ∠ABC + ∠ADC + (∠ACB + ∠ACD) = 180° + 180°

∴ ∠BAD + ∠ABC + ∠ADC + ∠BCD = 360°

The sum of measurement of all angles of a quadrilateral = 360°

Example 7. In ΔABC, the internal bisectors of ∠ABC and ∠ACB intersect at O, If ∠BOC = 105°, then find the value of ∠BAC.

Solution:

In ΔABC, BO, and CO are the bisectors of ∠ABC and ∠ACB respectively.

∴ ∠OBC = \(\frac{1}{2}\)∠ABC and ∠OCB =\(\frac{1}{2}\)∠ACB

∠OBC + ∠OCB = \(\frac{1}{2}\)(∠ABC + ∠ACB)

180° – ∠BOC = \(\frac{1}{2}\)(180° – ∠BAC)

180° – 105° = 90° – \(\frac{1}{2}\)∠BAC

75° = 90° – \(\frac{1}{2}\)∠BAC

⇒ \(\frac{1}{2}\)∠BAC = 90° – 75° = 15°

⇒ ∠BAC = 15° x 2 = 30°

The value of ∠BAC = 30°

Example 8. In ΔPQR, the internal bisector of ∠PQR and the external bisector of ∠PRQ intersect at T. If ∠QPR = 40° then find the value of ∠QTR.

Solution:

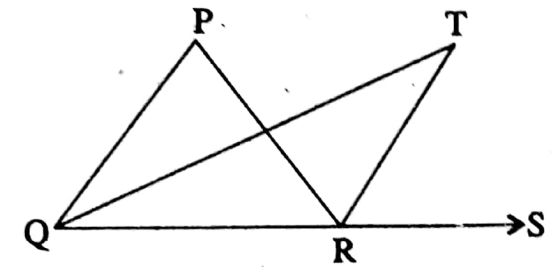
In ΔPQR,

⇒ ∠QTR + ∠TQR = exterior ∠TRS

⇒ ∠QTR = \(\frac{1}{2}\)∠PRS –\(\frac{1}{2}\)∠PQR

⇒ \(\frac{1}{2}\) (∠QPR + ∠PQR) – \(\frac{1}{2}\)∠PQR

= \(\frac{1}{2}\)∠QPR + \(\frac{1}{2}\)∠PQR – \(\frac{1}{2}\)∠QPR = \(\frac{1}{2}\) x 40° = 20°

The value of ∠QTR = 20°

Example 9. In ΔABC, AB = AC and ∠ABC = 2∠BAC. The bisector of ∠ABC meets AC at D. Find the measurement of the angles of the triangle BCD.

Solution:

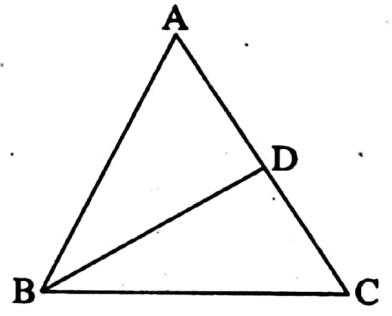
In ΔABC, AB = AC

∴ ∠ABC = ∠ACB

∠ABC + ∠ACB + ∠BAC = 180°

∠ABC + ∠ABC + ∠BAC = 180°

∴ 2∠BAC + 2∠BAC + ∠BAC = 180°

⇒ 5∠BAC = 180°

⇒ ∠BAC = \(\frac{180^{\circ}}{5}=36^{\circ}\)

∴ ∠ABC = ∠ACB = 2 x 36° = 72°

∠DBC = \(\frac{1}{2}\)∠ABC = \(\frac{1}{2}\) x 72° = 36°

In ΔBDC, ∠BDC + ∠DBC + ∠DCB = 180°

∠BDC + 36° + 72° 180°

∠BDC = 180° – 108° = 72°

∴ ∠DBC = 36°, ∠BDC = 72° and ∠DCB = 72°

The measurement of the angles of the triangle BCD = 72°

Example 10. ΔPQR, If ∠P = 80° and ∠Q= 70°, then find the relation between PQ and QR.

Solution:

In ΔPQR, ∠P = 80°, ∠Q = 70°

∴ ∠R = 180° – (80° + 70°) = 30°

As ∠P > ∠R

∴ QR > PQ (This the relation)

The relation between PQ and QR is QR > PQ

Example 11. The hypotenuse of a right-angled triangle is the greatest one – Explain.

Solution:

In ΔABC, ∠ABC = 90°

∴ AC is the hypotenuse.

∠A and ∠C each are acute angles.

∴ ∠ABC > ∠A and ∠ABC > ∠C

As ∠ABC > ∠A, ∴ AC > BC

As ∠ABC > ∠C  ∴ AC > AB

∴ AC is the largest side.

Example 12. If the ratio of measurement of angles of a triangle is 4: 5: 9; then write the nature of the triangle.

Solution: Let the measurement of three angles are 4x°, 5x° and 9x°

4x° +5x° + 9x° = 180°

⇒ 18x° = 180°

⇒ x° = 10°

The angles are 4 x 10° or 40°, 5 x 10° or 50° and 9 x 10° or 90°.

∴ The triangle is a right-angled triangle.

Example 13. ΔABC, if the bisector of ∠BAC and a parallel line of AB be drawn through P, the midpoint of AC intersect each other at a point E. Prove that ∠AEC = 90°.

Solution:

Given: In ΔABC, AE is the bisector of ∠BAC and D is the midpoint of AC.

DE || AB, I join E, C.

RTP:  ∠AEC = 90°

Proof: AB || DE (Given) and AE is transversal.

∴ ∠BAE = ∠AED [Alternate angles]

Again ∠BAE= ∠DAE [AE is bisector of ∠BAC]

∴ ∠AED = ∠DAE  ∴AD = DE

Again AD = DC [given]

∴ DE = DC,  ∴ ∠DEC = ∠DCE

∠AED + ∠DEC = ∠DAE + ∠DCE

i.e. ∠AEC = ∠CAE + ∠ACE

In ΔAEC, ∠AEC + ∠CAE + ∠ACE = 180°

∠AEC + ∠AEC = 180°

2∠AEC = 180°

⇒ ∠AEC = \(\frac{180^{\circ}}{2}\)

⇒ ∠AEC = 90° (Proved).

Example 14 The external bisectors of ∠ABC and ∠ACB of ΔABC meet at O. Prove that ∠BOC = 90° – \(\frac{1}{2}\)∠BAC

Solution: Given AB and AC are extended respectively.

BO and CO are the external bisectors of ∠ABC and ∠ACB of ΔABC.

RTP: ∠BOC = 90° – \(\frac{1}{2}\)∠BAC

Proof: BO and CO are the bisectors of ∠OBC

= \(\frac{1}{2}\)∠EBC and ∠OCB = \(\frac{1}{2}\)∠BCF

∠OBC + ∠OCB = \(\frac{1}{2}\)∠EBC + \(\frac{1}{2}\)∠BCF

= \(\frac{1}{2}\)(180° – ∠ABC) + \(\frac{1}{2}\)(180° – ∠ACB)

= 90° – \(\frac{1}{2}\)∠ABC + 90° – \(\frac{1}{2}\)∠ACB = 180° –\(\frac{1}{2}\) (∠ABC + ∠ACB)

= 180° – \(\frac{1}{2}\)(180° – ∠BAC) = 180° – 90° + \(\frac{1}{2}\)∠BAC

= 90° + \(\frac{1}{2}\)∠BAC

In ΔBOC,

∠BOC + ∠OBC + ∠OCB = 180°

∠BOC + 90° + \(\frac{1}{2}\)∠BAC = 180°

⇒ ∠BOC = 180°- 90° – \(\frac{1}{2}\)∠BAC

⇒ ∠BOC = 90° – \(\frac{1}{2}\)∠BAC (Proved)

Example 15. In ΔABC, AD is the bisector of the angle ∠BAC and AP ⊥ BC; if AB > AC then prove that ∠PAD = \(\frac{1}{2}\) (∠ACB – ∠ABC)

Solution:

Given: In ΔABC, AD is the bisector of ∠BAC and AP ⊥ BC.

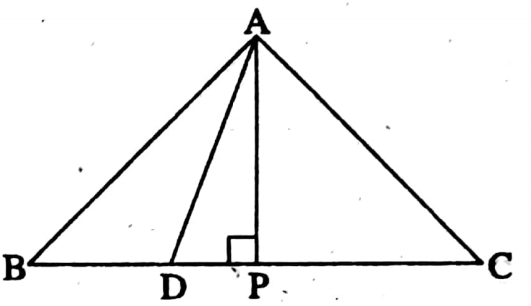
RTP: ∠PAD =\(\frac{1}{2}\) (∠ACB – ∠ABC)

Proof: AP ⊥ BC,  ∴  ∠APB = ∠APC = 90°

In ΔABP, ∠APB = 90°,

∴ ∠BAP + ∠ABP = 90°

In ΔAPC, ∠APC = 90°,

∴ ∠PAC + ∠ACP = 90°

∴ ∠PAC + ∠ACP = 90°

∴ ∠PAC + ∠ACP = ∠BAP + ∠ABP

⇒ ∠ACP – ∠ABP = ∠BAP – ∠PAC

= ∠BAD + ∠PAD – ∠PAD

= ∠CAD + ∠PAD – ∠PAC  [∠BAD = ∠CAD]

= (∠CAD – ∠PAC) + ∠PAD = ∠PAD + ∠PAD = 2∠PAD

⇒ ∠PAD = \(\frac{1}{2}\)(ACP – ABP)

∴ ∠PAD = \(\frac{1}{2}\) (∠ACB + ∠ABC)(Proved)

Example 16. In ΔABC, the bisectors of ∠ABC and ∠ACB meet at O. If AB > AC then prove that OB > OC.

Solution:

Given: In ΔABC, AB > AC; OB and OC are the bisectors of ∠ABC and ∠ACB respectively.

RTP: OB > OC

Proof: AB > AC

∴ ∠ACB > ∠ABC = ∠ACB > \(\frac{1}{2}\)∠ABC

∴ ∠OCB > ∠OBC

∴ OB > OC (Proved)

Example 17. AB is the greatest side and DC is the smallest side. Prove that ∠BCD > ∠BAD.

Solution:

Given: In quadrilateral ABCD, AB and DC are the greatest and smallest side respectively.

RTP: ∠BCD > ∠BAD

Construction: I join A, C.

Proof: In ΔABC, AB > BC [As AB is greatest side]

∴ ∠ACB > ∠BAC

In ΔACD, AD > DC  [DC is the smallest side]

∴ ∠ACD > ∠CAD    ∠ACB + ∠ACD > ∠BAC + ∠CAD

i.e. ∠BCD > ∠BAD (Proved)

Example 18. Choose the Correction Answer:

1. In ΔABC, AB = AC, BC is produced to D. If ∠ACD = 112° then the value of ∠BAC is

1. 44°
2. 68°
3. 22°
4. 34°

Solution:

∠ACD + ∠ACB = 180°

112° + ∠ACB = 180°

or, ∠ACB= 180° – 112° = 68°

In ΔABC, AB = AC, ∴ ∠ABC = ∠ACB = 68°

In ΔABC, exterior ∠ACD = ∠BAC + ∠ABC

112° = ∠BAC + 68°

⇒ ∠BAC = 112° – 68° = 44°

∴ So the correct answer is 1. 44°

The value of ∠BAC is 44°

2. In ΔABC, If ∠A = 70° and ∠B = 60°, then the relation between AB and BC is

1. AB = BC
2. AB > BC
3. AB < BC
4. None of these

Solution:

In ΔABC, ∠A + ∠B + ∠C = 180°

70° + 60° + ∠C = 180°

⇒ ∠C = 180° – 130° = 50°

The relation between AB and BC is

As, ∠A > ∠C

∴ BC > AB ⇒ AB > BC

∴ So the correct answer is 3. AB < BC

The relation between AB and BC is  AB < BC

3. If the measurement of an angle of a triangle is equal to sum of the other two angles, then the triangle becomes

1. Acute angled triangle
2. Obtuse angled triangle
3. Equilateral triangle
4. Right-angled triangle

Solution: In ΔABC, ∠A = ∠B + ∠C

∠A + ∠B + ∠C = 180°

∠A + ∠A = 180°

⇒ 2∠A = 180°

⇒ ∠A = 90°

The triangle is right angled triangle.

∴ So the correct answer is 4. Right angled triangle

Example 19. Write ‘True’ or ‘False’:

1. If the ratio of measurements of three angles of a triangle is 1: 2: 3, then the triangle becomes right angled triangle.

Solution: Let the angles are x°, 2x°, and 3x°.

x + 2x + 3x = 180

⇒ 6x = 180 ⇒ x = 30.

∴ The angles are 30°, 30° x 2 or 60° and 30° x 3 or 90°.

∴ The triangle is right angled triangle.

∴ So the statement is true.

2. If PQ || TS, then the value of x is 80°.

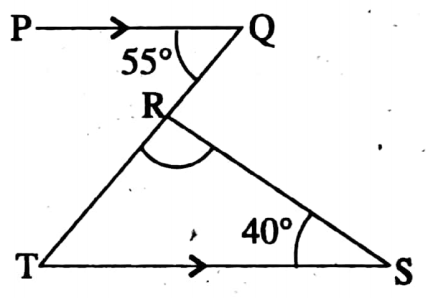
Solution: ∠QTS = ∠PQT [Alternate angle] = 55°

i.e. ∠RTS = 55°

∠TRS + ∠RTS + ∠RST = 180°

x + 55° + 40° = 180°

⇒ x = 180° – 95° = 85°

∴ So the statement is false.

Example 20. Fill in the blanks:

1. In obtuse angled triangle opposite side of _______ is largest.

Answer: Obtuse angle.

Solution: Let, In ΔABC, ∠B is obtuse angle.

∴ ∠A and ∠C are both acute angle.

∴ ∠B > ∠A and ∠B > ∠C

As ∠B > ∠C then AC > AB

∴ AC is largest.

∴ The obtuse angled triangle opposite side of obtuse angle is largest.

2. In ΔABC, AB = AC; BC is produced to D. If ∠ACD = 105° then the value of ∠BAC

Solution:

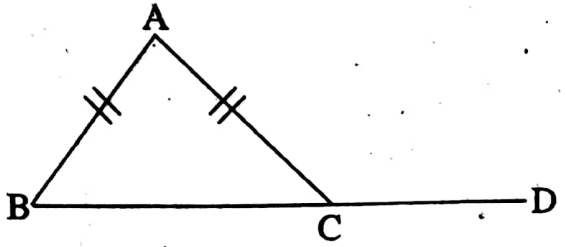
In, ΔABC, ∠ACD = 105°

∠ACB = 180° – ∠ACD = 180° – 105° = 75°

AB = AC

∴ ∠ABC = ∠ACB = 75°

∠BAC + ∠ABC = Exterior ∠ACD

∠BAC + 75° = 105°

⇒ ∠BAC = 105° – 75° = 30°.

The value of ∠BAC = 30°.