WBBSE Solutions For Class 8 Maths Geometry Chapter 7 Geometrical Proofs

Geometry Chapter 7 Geometrical Proofs

⇒ Polygon: A plane figure bounded by three or more than three line segment is called a polygon.

⇔ If a polygon has three sides, it is called a triangle.

⇔ Similarly quadrilateral has four sides, pentagon has five sides, hexagon has six sides etc.

⇒ Regular Polygon: A polygon whose all sides are equal in length and the measurement of all angles are equal is called regular polygon.

Example: Regular triangle is an equilateral triangle whose each angle is 60°.

⇔ Square is a regular quadrilateral whose each interior angle is 90°.

Read and Learn More WBBSE Solutions For Class 8 Maths

[Rhombus is not a regular quadrilateral because although the length of four sides are equal but the measurement of each angle are not equal]

Theorem 1. The sum of length of any two sides is greater than length of the third side.

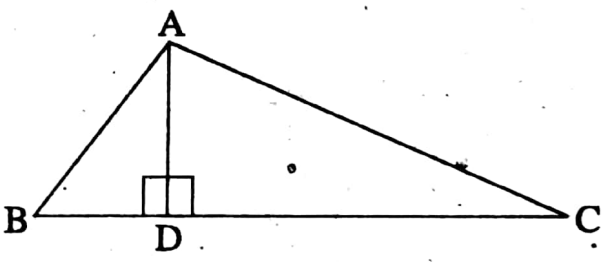
Given: Let BC is the longest side of ΔABC.

Required to prove: If we prove AB + AC > BC then it.

Will be proved that the sum of lengths of any two sides of a triangle is greater than the length of the third side.

Construction: We draw a perpendicular AD on BC from the point A which intersects BC at D.

Proof: As AD ⊥ BC [By construction]

∴ ∠ADB = ∠ADC = 90°

In ΔABD, ∠ADB is right angle and ∠BAD is an acute angle.

∴ ∠ADB > ∠BAD

∴ AB > BD [The opposite side of bigger angle is greater than the opposite side of smaller angle]

⇔ In ΔADC, ∠ADC is right angle and ∠CAD is an acute angle.

∴ ∠ADC > ∠CAD

∴ AC > CD

∴ AB+ AC > BD + CD

i.e. AB+ AC > BC (Proved)

WBBSE Class 8 English Functional Grammar	WBBSE Class 8 English Reading Skills
WBBSE Solutions For Class 8 English	WBBSE Solutions For Class 8 Maths

 

Theorem 2. The sum of the measurement of all the interior angles of a polygon of sides n is 2(n-2) right angles.

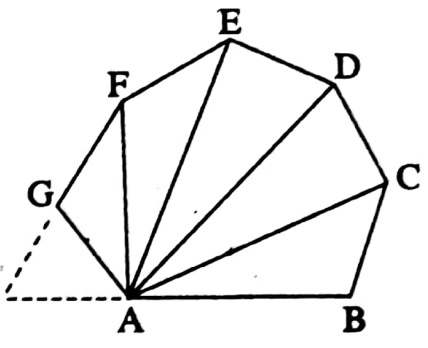
Given: Let’s ABCDEFG…. be a polygon with n sides.

Required to prove: Sum of the measurement of all the interior angles of the polygon with n. sides is 2(n − 2) right angles.

Construction: I draw the diagonals AC, AD, AE, AF, AG,…

Proof: By joining the vertex A with other vertices C, D, E, F, G…. of the polygon i.e. by construction the diagonals AC, AD, AE, AF, AG, . . . . . . of the polygon with n sides (n-2) number of triangles are formed.

∴ Sum of the measurement of all the interior angles of the polygon ABCDEFG…. is

= Sum of the measurement of interior angles of (n-2) triangles.

= (n -2) x 2 right angles = 2 (n-2) right angles. (Proved)

Theorem 3. All the line segments drawn from a point outside a straight line to any point on the straight line perpendicular is smallest one.

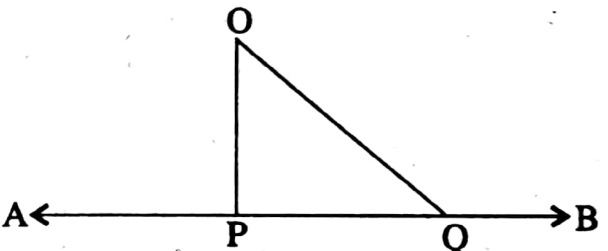
Given: Let AB be a straight line and O be a point outside of line AB and OP ⊥ AB.

Required to prove: It is to be proved that any line segment drawn from a point O to the straight line AB, the smallest one is OP.

Construction: Let Q is a point on the straight line AB other than the point P.

I join O and Q.

Proof: In ΔPOQ, ∠OPQ = 90°  [OP ⊥ AB]

∠OPQ > ∠OQP [∠OQP is an acute angle]

∴ OQ > OP [The length of opposite side of a greater angle is greater than the side opposite to smaller angle]

Q is any point on the straight line AB other than P.

∴ For any point Q on AB, OP < OQ.

∴ OP is the smallest. (Proved)

1. In a regular polygon of n sides measurement of each interior angle is \(\frac{2(n-2)}{2}\) x 90° and the measurement of each exterior angle is \(\frac{360^{\circ}}{n}\)
2. In ΔABC, if ∠ABC= 90°, then AB²+ BC² = AC² [By Pythagoras theorem]

Geometry Chapter 7 Geometrical Proofs Examples

Example 1. From the length of the following sides, in which case is it possible to draw a triangle?

1. 3 cm, 4 cm, 7 cm
2. 5 cm, 6 cm, 4 cm
3. 4.5 cm, 5 cm, 10 cm
4. 6 cm, 8 cm, 10 cm

Solution: The sum of the length of any two sides is greater than length of the third side.

1. 3 + 4 = 7

⇔ In this case it is not possible to draw a triangle.

2. 5+ 6 > 4, 4 + 5 > 6 and 6 + 4 > 5

⇔ In this case it is possible to draw a triangle.

3. 4.5+ 5 < 10

⇔ In this case it is not possible to draw a triangle.

4. 6 + 8 > 10, 6 + 10 > 8, 8 + 10 > 6

⇔ In this case it is possible to draw a triangle.

Example 2. Find the sum of measurement of all the interior angles of the following polygons:

1. Octagon
2. Decagon
3. Polygon with 12 sides
4. Polygon with 15 sides.

Solution:

1. The sum of measurement of all the interior angles of a octagon is 2(8-2) × 90° = 2 x 6 x 90° = 1080°.
2. Sum of measurement of all the interior angles of a decagon is 2 (10-2) × 90° = 2 x 8 x 90° = 1440°
3. Sum of measurement of all the interior angles of polygon with sides 12 is 2(12-2) × 90° = 2 x 10 x 90° = 1800°
4. Sum of measurement of all the interior angles of polygon with side 15 is 2(15-2) × 90° = 2 x 13 x 90° = 2340°

Example 3. Find the measurement of each interior and exterior angle of the following regular polygon.

1. Pentagon
2. Hexagon
3. Polygon with side 25

Solution:

1. The measurement of each interior angle of pentagon is

\(\frac{2(5-2)}{5} \times 90^{\circ}=2 \times \frac{3}{5} \times 90^{\circ}=108^{\circ}\)

Measurement of each exterior angle of pentagon is \(\frac{360^{\circ}}{5}=72^{\circ}\)

2. The measurement of each interior angle of hexagon is

\(\frac{2(6-2)}{6} \times 90^{\circ}\) = \(\frac{2 \times 4 \times 90^{\circ}}{6}\) =120°

And each exterior angle is \(\frac{360^{\circ}}{6}=60^{\circ}\)

3. The measurement of each interior angle of polygon with 25 side is

\(2 \times \frac{(25-2)}{25} \times 90^{\circ}=2 \times \frac{23}{25} \times 90^{\circ}=\frac{828^{\circ}}{5}=165.6^{\circ}\)

And each exterior angle is \(\frac{360^{\circ}}{25}=14.4^{\circ}\)

Example 4. If the measurement of three angles of a quadrilateral are 100°, 62°, and 85° respectively, then find the measurement of the fourth angle.

Solution: The sum of the measurement of three angle is (100° + 62° + 85°) = 247°

⇔ The sum of measurement of all interior angles of a quadrilateral is 2(4 – 2) x 90° =360°

⇔ So the measurement of fourth angle is (360° – 247°) = 113°

Example 5. If sum of measurement of all interior angles of a polygon is 1440°, then find number of sides of the polygon.

Solution: Let the number of sides of the polygon is n.

∴ Sum of measurement of all interior angles is (2n – 4) x 90°

⇔ According to the question,

(2n – 4) x 90° = 1440°

⇒ 2n – 4 = \(\frac{1440}{90}\) = 16

⇒ 2n = 16+ 4 = 20

⇒ n = \(\frac{20}{2}\) = 10

∴ The number of sides of the polygon is 10.

Example 6. Find whether the following measurement are possible or not for exterior angle of a regular polygon.

1. 15°
2. 28°

Solution:

1. Exterior angle of the regular polygon is 15°.

∴ The number of sides = \(\frac{360^{\circ}}{15^{\circ}}\) = 24

Hence 15° is the measure of an exterior angle of a regular polygon of sides 24.

2. Each exterior angle is 28°.

∴ The number of sides = \(\frac{360}{28}=\frac{90}{7}=12 \frac{6}{7}\)

⇔ But the number of sides cannot be a fraction.

⇔ Hence 28° cannot be the measure of an exterior angle of a regular polygon.

Example 7. Find whether the following measurement of each interior angle is possible for a regular polygon.

1. 144°
2. 155°

Solution:

1. The measurement of each interior angle of a regular polygon is 144°.

∴ The measurement of each exterior angle is (180° – 144°) or 36°.

∴ The number of sides = \(\frac{360}{36}\) = 10

So 144° is the measure of interior angle of a regular polygon of sides 10.

2. Each interior angle is 155°.

∴ Each exterior angle is (180° – 155°) or 25°.

The number of sides = \(\frac{360}{25}\) = \(\frac{72}{5}\) = 14\(\frac{2}{5}\) which is fraction.

∴ 155° cannot be the measure of an interior angle of a regular polygon.

Example 8. Measurement of each of 4 interior angle is 150° and measurement of each of the other interior angle of a polygon is 100°. Find the number of sides of the polygon.

Solution: Let the number of sides be n.

⇒ So the number of interior angles becomes n.

⇒ Sum of measurement of interior angles of n sides is 2 (n – 2) x 90°.

⇒ Sum of measurement of first 4 interior angles is 4 x 150° or 600°.

⇒ Sum of measurement of rest (n – 4) interior angles is (n – 4) x 100°.

According to question,

= 2(n-2) x 90° = 600° + (n-4) x 100°

⇒ 2(n-2) x 9 = 60 + (n-4) × 10

⇒ 18n – 36 = 60 + 10n – 40

⇒ 18n – 10n = 20 + 36

⇒ 8n = 56 ⇒ n = 7

∴ The number of sides of the polygon is 7.

Example 9. In the adjacent ABCDE is a regular pentagon. Find the value of ∠CAD.

 

 

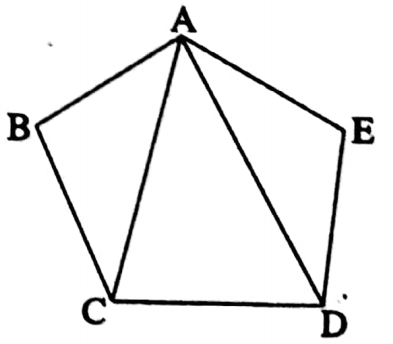
Solution: The measurement of each interior angle of a regular pentagon is

\(\frac{2(5-2) \times 90^{\circ}}{5}=\frac{2 \times 3 \times 90^{\circ}}{5}=108^{\circ}\)

∴ \(\angle \mathrm{ABC}=\angle \mathrm{BAE}=\angle \mathrm{AED}=108^{\circ}\)

\(\text { In } \triangle \mathrm{ABC}, \mathrm{AB}=\mathrm{BC}\)

∴ \(\angle \mathrm{BAC}=\angle \mathrm{ACl}\)

\(\angle \mathrm{BAC}+\angle \mathrm{ABC}+\angle \mathrm{ACB}=180^{\circ}\) \(\angle \mathrm{BAC}+108^{\circ}+\angle \mathrm{BAC}=180^{\circ}\) \(2 \angle \mathrm{BAC}=180^{\circ}-108^{\circ}=72^{\circ}\)

∠BAC = \(\frac{72^{\circ}}{2}=36^{\circ}\)

Similarly ∠DAE = 36°

⇒ ∠BAC + ∠CAD + ∠DAE= 108°

⇒ 36° + ∠CAD + 36° = 108°

⇒ ∠CAD = 108° – 72° = 36°

The value of ∠CAD = 36°

Example 10. In the adjacent, the shortest distance of point P from the straight line AB is 3 cm and length of QR is 4 cm. Find the length of PR.

 

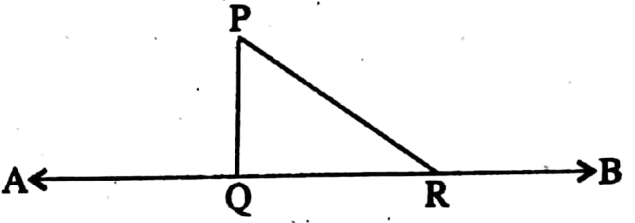
Solution: The shortest distance of point P from the straight line AB is PQ.

∴ PQ ⊥ AB.

∴ ∠PQR = 90°

PQ = 3cm, QR = 4cm

∴ In ΔPQR,

⇒ PR² = PQ² + QR² [By applying pythagorus A theorem]

= (3²+4²) sq.cm. = 25 sq.cm.

PR = √25 cm = 5 cm.

∴ The length of PR is 5 cm.

Example 11. Prove that the sum of lengths of two diagonals of a quadrilateral is greater than the semi-perimeter of the quadrilateral.

Solution:

Given: Two diagonal AC and BD of a quadrilateral ABCD intersect at O.

 

 

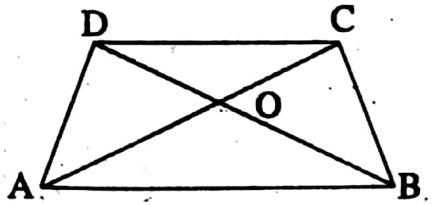
RTP: AC + BD > \(\frac{1}{2}\)(AB + BC + CD + DA)

Proof: In ΔAOB, OA + OB > AB…… (1)

[The sum of lengths of any two sides of a triangle is greater than the length of the third side]

⇒ In ΔBOC, OB + OC > BC…….(2)

⇒ ΔCOD, OC + OD > CD…….(3)

⇒ In ΔAOD, OD + OA > DA…….(4)

∴ (1) + (2) + (3) + (4), we get

⇒ 2(OA + OC + OB + OD) = AB + BC + CD + DA

∴ 2(AC+ BD) = AB + BC + CD + DA

⇒ AC + BD = \(\frac{1}{2}\)(AB + BC + CD + DA) (Proved)

Example 12. Prove that the perimeter of a triangle is more than the sum of length of the medians.

Solution: Given: In ΔABC, AD, BE and CF are three medians.

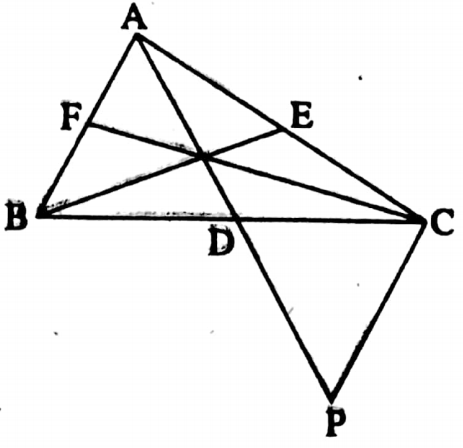
RTP: AB+ BC + CA > AD + BE + CF

Construction: I produced the line segment AD to P in such a way that AD = DP.

I join P, C.

Proof: In ΔABD and ΔPCD,

⇒ BD = CD (Given)

⇒ ∠ADB = ∠PDC [Vertically opposite angles]

and AD = DP [By construction]

∴ ΔABD ≅ ΔPCD [By SAS congruency]

∴ AB = CP (Corresponding sides]

⇒ In ΔAPC, AC + CP > AP AC + AB > AD + DP

∴ AC + AB > AD + AD

∴ AB + AC > 2AD……..(2)

⇒ Similarly, AB + BC > 2BE…..(2)

and BC + AC > 2CF…..(3)

(1) + (2) + (3) we get

2(AB + BC + AC) > 2(AD + BE + CF)

⇒ AB + BC + CA > AD + BE + CF (Proved)

Example 13. In a quadrilateral ABCD, AB = AD and BC = DC, and DP is the smallest distance drawn from D on AC. Prove that B, P, and D are collinear.

Solution:

Given: In a quadrilateral ABCD, AB = AD, BC = DC and DP is the smallest distance drawn from D on AC.

I Join B, P.

 

 

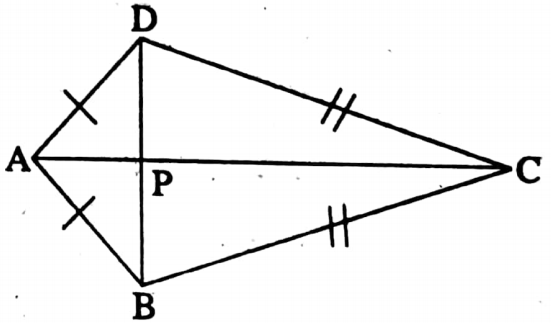
RTP: B, P, and D are collinear.

Proof: As DP is the shortest distance.

∴ DP ⊥ AC.

∴ ∠APD = ∠CPD = 90°

In ΔABC and ΔADC, AB = AD (given)

BC = DC (given) and AC is common side.

∴ ΔABC ≅ ΔADC [By SSS congruency]

∴ ∠BAC = ∠DAC [Corresponding angles]

∴ i.e. ∠BAP = ∠DAP

In ΔAPB and ΔADP,

⇒ AB = AD ΔBAP = ΔDAP and AP is common side.

∴ ΔAPB ≅ ΔADP [By SAS congruency]

∴ ∠APB + ∠APD  ∠APB = 90°

∠APB + ∠APD = 90° + 90° = 180°

∴ BP and DP lies in straight line.

∴ B, P, D are collinear. (Proved)

Example 14. O is any point inside the ΔABC. Prove that AB + BC + CA > OA + OB + OC.

Solution:

 

 

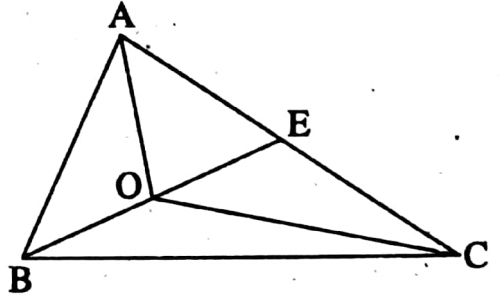
Given: O is any point inside the ΔABC.

I join OA; OB and OC.

RTP: AB+ BC + CA > OA + OB + OC

Construction: BO is produced which meets AC at E.

Proof: In ΔCOE, OE + EC > OC

In ΔABE, AB + AE > BE

∴ OE+ EC + AB+ AE > OC+ BE

OE + (EC+ AE) + AB > OC + OB + OE

∴  OE + AC+ AB > OB + OC + OE

∴ AB + AC > OB + OC……. (1) [Subtracting OE from both side]

Similarly,

AB + BC > OA + OC ….. (2)

and AC + BC > OA + OB…. (3)

(1) + (2) + (3), we get,

2(AB + BC + CA) > 2 (OA + OB + OC) AB + BC + CA > OA + OB + OC

Example 15. Choose the correct answer:

1. The sum of measurement of all the interior angles of a hexagon is

1. 360°
2. 720°
3. 540°
4. 1080°

Solution: The sum of measurement of interior angle of a hexagon is 2(6 – 2) × 90° = 2 x 4 x 90° = 720°

∴ So the correct answer is 2. 720°

The sum of measurement of all the interior angles of a hexagon is  720°.

2. The measurement of each interior angle of a regular decagon is

1. 144°
2. 108°
3. 120°
4. 72°

Solution: The measurement of each interior angle of regular decagon is

\(\frac{2(10-2) \times 90^{\circ}}{10}=\frac{2 \times 8 \times 90^{\circ}}{10}=144^{\circ}\)

∴ So the correct answer is 1. 144°

The measurement of each interior angle of a regular decagon is 144°.

3. If the measurement of each exterior angle is 72°, the number of side is

1. 12
2. 10
3. 5
4. 6

Solution: The number of side = \(\frac{360^{\circ}}{72^{\circ}}=5\)

∴ So the correct answer is 3. 5

The number of side is 5.

Example 16. Write ‘True’ or ‘False’:

1. In a regular polygon of n sides measurement of each exterior angle is \(\frac{360^{\circ}}{n}\)

Solution: The sum of measurement of all the interior angles of a regular polygon is 2(n-2) x 90°.

∴ The measurement of each angle is \(\frac{2(n-2) \times 90^{\circ}}{n}\)

The sum of interior and exterior angle is 180°.

∴ The exterior angle is 180° – \(\frac{2(n-2) \times 90^{\circ}}{n}=\frac{180 n-180 n+360^{\circ}}{n}=\frac{360^{\circ}}{n}\)

∴ So the statement is true.

2. If the measurement of each interior angle of a regular polygon is 120°, then the number of sides of the polygon is 6.

Solution: Exterior angle is 180° – 120° = 60°

The number of side = \(\frac{360^{\circ}}{60^{\circ}}=6\)

∴ So the statement is true.

Example 17. Fill in the blanks:

1. The measurement of each angle of regular quadrilateral is _______

Solution: The measurement of each angle of regular quadrilateral is \(\frac{360^{\circ}}{4}=90^{\circ}\)

2. The perimeter of a quadrilateral is greater than _______ the length of any one of the diagonals.

Solution:

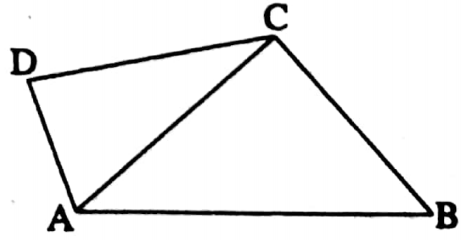
In ΔABC, AB + BC > AC

In ΔADC, AD + CD > AC

AB + BC + AD + CD > AC + AC

AB + BC + CD + AD > 2AC

∴ The perimeter of the quadrilateral is greater than twice the length of any one of the diagonals.