WBBSE Solutions For Class 9 Maths Arithmetic Chapter 1 Real Numbers

Arithmetic Chapter 1 Real Numbers

⇔ Natural Numbers: 1, 2, 3, 4, 5,………………… 125, ………….. are counting numbers or natural numbers such that 1 is the first natural number and there is no last natural number.

⇒The natural number is denoted by N and is written as

⇒ N = (1, 2, 3, 4, ……………..,125,………………….).

⇔ Whole numbers: The numbers 0, 1, 2, 3,……………, 125,……… are called whole numbers.

⇒ The whole numbers is denoted by W and is written as

⇒ W = (0, 1, 2, 3, 125,…..)

⇔ Integers: The numbers……., -4, -3, -2, -1, 0, 1, 2, 3…….are called Integers.

⇒ The integers is denoted by Z and is written as Z = (…….., -3, -2, -1, 0, 1, 2, 3,………..)

WBBSE Solutions For Class 9 Maths

⇒ The integers greater than 0, i.e. 1, 2, 3,……. are called Positive Integers and the integers less than 0, i.e.-1,2,3,….. are called Negative Integers.

⇒ 0 (Zero) is an integer that is neither positive nor negative.

⇔ Rational Numbers: The numbers which can be expressed in the form of \(\frac{p}{q}\) where p and q are integers and q 0 are called Rational Numbers. eg: 6, \(\frac{3}{4}\), 0, \(\frac{5}{6}\) etc.

⇒ [All integers are Rational Numbers.]

⇔ Irrational Numbers: The numbers which can not be expressed in the form of \(\frac{p}{q}\) where p and q are integers and q #0 are called Irrational Numbers. e.g. √3, π etc.

Some important points:

1. If two rational numbers x and y such that x < y there is a rational number \(\frac{x+y}{2} \text { i.e. } x<\frac{x+y}{2}<y\)
2. If x and y are two rational numbers and x < y then, n rational numbers between x and y are (x + d), (x + 2d), (x + 3d),….. (x + nd), where d = \(d=\frac{y-x}{n+1}\)
3. If the rational numbers of the form \(\frac{p}{q}\) be expressed into decimals, it will be terminating decimal numbers, where q has prime factors 2 and 5 only.
4. If the rational numbers of the form \(\frac{p}{q}\) be expressed into recurring decimals where q has prime factors other than 2 and 5.
5. If rational numbers are expanded into decimals it will be terminating are recurring and the fraction whose decimal form is terminating or recurring will be rational.

Arithmetic Chapter 1 Real Numbers True Or False

Example 1. The sum of two rational numbers is always rational.

Solution: The statement is true.

⇒ [e.g. [\(\frac{5}{7}\) + \(\frac{2}{3}\) = \(\frac{29}{21}\)]

Example 2. The sum of two irrational numbers is always irrational.

Solution: The statement is false.

⇒ [6.8. (2+√3)+(4-√3)=6]

Example 3. The product of two rational numbers is rational.

Solution: \(\frac{3}{4}\) x \(\frac{5}{6}\) = \(\frac{5}{6}\) [rational number]

∴ The statement is true.

Example 4. The product of two irrational numbers is always rational.

Solution: √3 × √5 = √15 [irrational number]

⇒ (3+√5)(3-√5)=(3)²-(√5)²

= 9 – 54 [rational number]

∴ The statement is false.

Example 5. Each rational number is real number.

Solution: \(\frac{3}{5}\), 0, √9, –\(\frac{4}{7}\) all are real number.

∴ So the statement is true.

Example 6. Each real number is irrational.

Solution: Clearly the statement is False.

Arithmetic Chapter 1 Real Numbers Fill In The Blanks

Example 1. The division of two integers is not always ______

Solution: Integer.

Example 2. The value of (2 + √3)(2 – √3) is ______

Solution: 1

(2 + √3)(2 -√3) = 2² – (√3)² = 4 – 3 = 1

Example 3. The difference between 1 and 0.9 is ________

Solution: 0

1 – 0.9 = 1 – \(\frac{9}{9}\) = 1 – 1 = 0

Example 4. We will get _______ decimal if \(\frac{7}{20}\) are expanded into decimal.

Solution: Terminating.

20 = 2² x 5

20 has no prime factors except 2 and 5.

∴ The decimal form of \(\frac{7}{20}\) will be terminating.

Arithmetic Chapter 1 Real Numbers Short Answer Type Questions

Example 1. Give an example where sum of two irrational numbers is a rational number.

Solution:

1. √5, -√5 √5 + (-√5) = 0 [rational number]
2. 7 + √5; 7 – √5 (7 + √5) + (7 – √5) = 14 [rational number]

Example 2. Give an example where subtraction of two irrational number is a rational number.

Solution:

1. √7, √7 ⇒ √7-√7=0 [rational number]
2. (5+√3), (2+√3) ⇒ (5+√3)-(2+√3) = 5 + √3 – 2 – √3 = 3 [rational number]

Example 3. Write a rational number between \(\frac{1}{7}\) and \(\frac{2}{7}\)

Solution: A rational number between \(\frac{1}{7}\) and \(\frac{2}{7}\) is \(\frac{\frac{1}{7}+\frac{2}{7}}{2}\) = \(\frac{3}{7 \times 2}=\frac{3}{14}\)

Example 4. Determine a irrational number between \(\frac{1}{7}\) and \(\frac{2}{7}\).

Solution: \(\frac{1}{7}\) = 0.1428571428571……..= 0.142857

⇒ \(\frac{2}{7}\) = 0.285714285714……= 0.285714

⇒ The irrational number lying between \(\frac{1}{7}\) and \(\frac{2}{7}\) will be non-terminating and non-recurring.

∴ One required irrational number is 0.15015001500015………..

Example 5. Express 0.0123 in the form of \(\frac{p}{q}\) where p and q are integers and q ≠ 0.

Solution: 0.0123 = \(\frac{0123-12}{9000}=\frac{111}{9000}=\frac{37}{3000}\)

Example 6. Write four rational numbers between 2 and 3.

Solution: If x and y are two rational numbers and x < y then, n rational numbers between x and y are (x + d), (x + 2d), (x + 3d)………..(x+nd.), where \(d=\frac{y-x}{x+1}\)

⇒ Here, x = 2, y = 3 and n = 4

⇒ d = \(\frac{3-2}{4+1}=\frac{1}{5}\)

∴ The four rational numbers are

⇒ \(\left(2+\frac{1}{5}\right)\left(2+\frac{2}{5}\right)\left(2+\frac{3}{5}\right),\left(2+\frac{4}{5}\right)\)

i.e. \(\frac{11}{5}, \frac{12}{5}, \frac{13}{5} \text { and } \frac{14}{5}\)

Example 7. Write four irrational numbers between \(\frac{2}{3}\) and \(\frac{5}{3}\)

Solution: \(\frac{2}{3}\) = 0·666…………..0.6

⇒ \(\frac{5}{3}\) = 1.666…………. = 1.6

⇒ The irrational number between \(\frac{2}{3}\) and \(\frac{5}{3}\) will be non-terminating and non-recurring.

∴ Four irrational numbers between \(\frac{2}{3}\) and \(\frac{5}{3}\) are 0.707007000700007……….

⇒ 0.72572557255572………, 0.81481448144481…………., 0.93293229322293……….

Example 8. Place the rational numbers on a Number line.

1. –\(\frac{3}{4}\)
2. \(\frac{13}{5}\)

Solution:

1.

⇒ At first, 9 take OA’ = 1 unit on the left side of the point ‘0’, OA’ is divided into 4 equal parts.

⇒ OR = –\(\frac{3}{4}\) unit.

2.

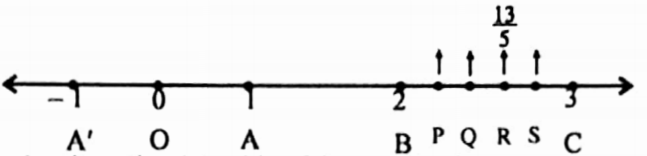
At first, 9 take OA 1 unit on the right side of the point ‘O’,

∴ OB = 2 units and OC = 3 units.

⇒ BC is divided into 5 equal parts BR = \(\frac{3}{5}\) unit.

∴ OR = OB + BR = = (2 + \(\frac{3}{5}\)) units = \(\frac{13}{5}\) units.

Example 9. Write two rational numbers between 0.2101 and 0.2

Solution: 0.2 = 0.2222………..

⇒ The two rational numbers between 0.2101 and 0.2 are 0.211 and 0.212

Example 10. Express each of the following numbers in the form of \(\frac{p}{q}\) where p and q are integers and q 0.

1. 0.2345
2. 12.0366

Solution:

1. 0.2345 = \(\frac{2345-234}{9000}=\frac{2111}{9000}\)
2. 12.0306 = \(\frac{120306-1203}{9900}=\frac{119103}{9900}=\frac{39701}{3300}\)