Geometry Chapter 1 Properties Of Parallelogram
⇔ Trapezium: A quadrilateral of which one pair of opposite sides are parallel is called Trapezium.

⇒ ABCD is a trapezium in which AB || DC
⇔ Isosceles trapezium: A trapezium of which non parallel sides are equal is called isosceles trapezium.
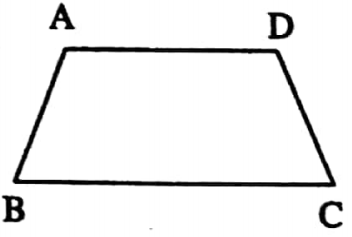
⇒ ABCD is an isosceles trapezium whose AD || BC and AB = DC
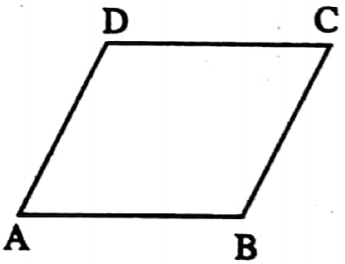
⇔ Parallelogram: The quadrilateral of which opposite sides are parallel is called parallelogram.
Read and Learn More WBBSE Solutions For Class 9 Maths

⇒ ABCD is a parallelogram whose AB || DC and AD || BC.
⇔ Rhombus: The parallelogram of which adjacent sides are equal in length is called Rhombus.
⇒ ABCD is a rhombus whose AB BC= CD = DA
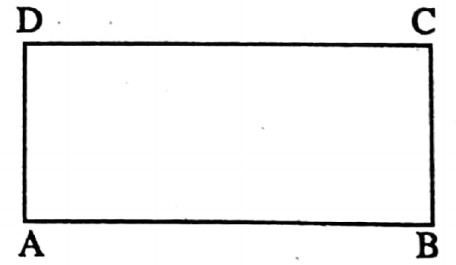
⇔ Rectangle: A parallelogram of which one angle is right-angle is called rectangle.

⇒ ABCD is a rectangle whose AB || DC, AD || BC, and ∠A = ∠B = ∠C = ∠D = 90°.
⇔ Square: The rectangle of which one pair of adjacent sides are equal in length is called square.
or, the Rhombus of which one angle is right-angle is called square.

⇒ ABCD is a square whose AB = BC = CD = DA and ∠A = ∠B = ∠C = ∠D = 90°.
⇔ Kite: The quadrilateral of which one pair of adjacent sides are equal and the remaining two sides are also equal in length is called kite.
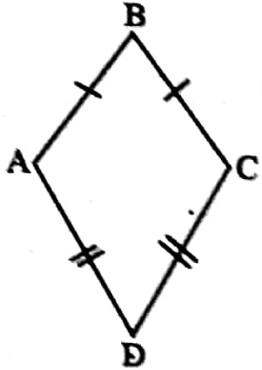
⇒ ABCD is a kite whose AB BC, AD CD but AB ≠ AD and BC ≠ CD
Theorem:
1. For any parallelogram:
- Each diagonal bisects it into congruent triangles.
- Opposite sides are equal
- Opposite angles are equal.
2. The diagonals of a parallelogram bisect each other.
3. If opposite sides of any quadrilateral are equal, then the quadrilateral will be a parallelogram.
4. If the opposite angles of a quadrilateral are equal, then this will be a parallelogram.
5. If one pair of opposite sides of any quadrilateral is equal as well as parallel then the quadrilateral will be a parallelogram.
6. If the two diagonals of a quadrilateral bisect each other, then the quadrilateral will be a parallelogram.
Geometry Chapter 1 Properties Of Parallelogram True Or False
Example 1. In parallelogram ABCD if ∠BAD = ∠ABC then parallelogram ABCD will be a rectangle.
Solution: In parallelogram ABCD,
⇒ ∠BAD + ∠ABC = 180°
⇒ ∠BAD + ∠BAD = 180° [ ∠BAD = ∠ABC]
⇒ 2 ∠BAD = 180°
⇒ ∠BAD = 90°
∴ Parallelogram will be a rectangle.
So the statement is true.
Example 2. In rectangle ABCD, if the diagonal AC is bisects angles ∠A and ∠C, then the rectangle ABCD will be a square.
Solution: The diagonal AC of rectangle ABCD is bisects the angles ∠A and ∠C.
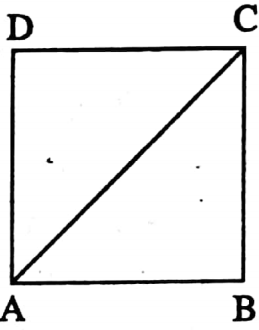
∴ ∠BAC = ∠DAC and ∠BCA = ∠DCA
⇒ Again, AB || DC and AC is the intersection
∴ ∠BAC = ∠DCA but ∠BAC = ∠DAC
∴ ∠DAC = ∠DCA
⇒ In ΔADC, ∠DAC = ∠DCA, ∴ DC = AD
⇒ but DC = AB and AD = BC
∴ AB = BC = CD
∴ ABCD is a square.
So the statement is true.
Geometry Chapter 1 Properties Of Parallelogram Fill In The Blanks
Example 1. The diagonals of a square or a rhombus bisect each other ________
Solution: Perpendicularly.
Example 2. The lengths of opposite sides of a kite is ________
Solution: Unequal.
Geometry Chapter 1 Properties Of Parallelogram Short Answer Type Questions
Example 1. In the parallelogram ABCD, ∠A: ∠B = 3: 2, write the measures of the angles of the parallelogram.
Solution: In parallelogram ABCD, ∠A: ∠B = 3:2
Let, ∠A = 3x° and ∠B = 2x° [x° is a common multiple and x > 0]
⇒ ∠A + ∠B = 180°
⇒ 3x° + 2x° = 180°
⇒ 5x = 180° ⇒ x° = 36°
∴ ∠D = ∠B = 2 x 36° = 72° [opposite angles of parallelogram are equal]
and ∠C = ∠A = 3 × 36° = 108°
∴ The measures of the angles of the parallelogram is 108°.
Example 2. In the parallelogram ABCD, the bisectors of ∠A and ∠B meets CD at the point E. The length of the side BC is 2 cm. Write the length of the side AB.
Solution: In parallelogram, AD = BC = 2 cm

As AE is the bisector of the ∠BAD
∴ ∠BAE = ∠DAE
⇒ Again, DC || AB and AE is the intersection
∴ ∠AED = alternate ∠BAE
∴ ∠AED = ∠DAE
∴ AD = DE = 2 cm [BC= 2 cm]
⇒ Similarly, CE = 2 cm
⇒ AB = DC = DE = CE = (2 + 2) cm = 4 cm.
∴ The length of the side AB is 4 cm.
Example 3. The equilateral triangle AOB lie within the square ABCD. Write the value of ∠COD.
Solution: In equilateral triangle ΔAOB, OA = AB = OB

and ∠AOB = ∠OAB = ∠OBA = 60°
⇒ ∠OBC = 90° – 60° = 30° [∠ABC = 90°]
⇒ In ΔBOC, OB = BC [OB = AB and AB = BC]
∴ ∠OCB = ∠BOC = \(\frac{180^{\circ}-30^{\circ}}{2}\) = 75°
⇒ ∠OCB = 90° – ∠OCB = 90° – 75° = 15°
⇒ Similarly, ∠ODC = 15°
⇒ In ACOD, COD = 180° – ∠OCD – ∠ODC
= 180° – 15° – 15° = 150°
∴ The value of ∠COD is 150°.
Example 4. In the square ABCD, M is a point on AD so that ∠CMD= 30°. The diagonal BD intersects CM at the point P. Write the value of ∠DPC.
Solution: As BD is a diagonal of square ABCD
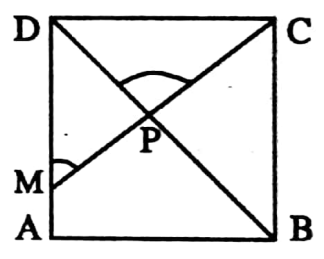
∴ ∠BDC= 45° i.e. ∠PDC= 45°
⇒ In ΔCMD, ∠CMD 30° and ∠MDC = 90°
⇒ ∠DCM = 180° (30° + 90°) = 60° i.e. ∠DCP = 60°
⇒ In ΔPDC, ∠PDC = 45°, ∠DCP = 60°
⇒ ∠DPC = 180° – (45° + 60°) = 75°
∴ The value of ∠DPC is 75°.
Example 5. In the rhombus ABCD, the length of the side AB is 4 cm, and ∠BCD = 60°. Write the length of the diagonal BD.
Solution: In rhombus ABCD, BC = CD = DA = AB = 4 cm
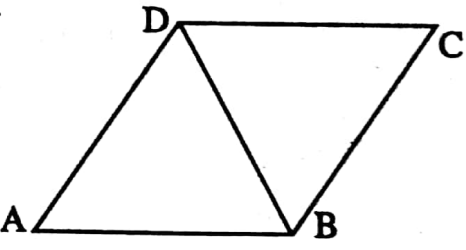
⇒ In ΔBCD, BC = DC
∴ ∠BDC = ∠DBC
⇒ ∠BCD = 60°
∴ ∠DBC = ∠BDC = \(\frac{180^{\circ}-60^{\circ}}{2}\) = 60°
⇒ ∠BCD = ∠DBC = ∠BDC
∴ BD = DC = BC 4 cm
∴ The length of the diagonal BD is 4 cm.
Example 6. In parallelogram ABCD, if ∠B = 60°, then write the measures of the angles of the parallelogram.
Solution: In parallelogram ABCD, ∠D = ∠B = 60°
⇒ ∠A + ∠B = 180° [as AD || BC and AB is intersection]
⇒ ∠A + 60° = 180° or, ∠A = 120°
∴ ∠C = ∠A = 120°
∴ The measures of the angles of the parallelogram is 120°.
Example 7. Determine the ∠PRQ of the parallelogram PQRS.
Solution: In parallelogram, ∠PSR = ∠PQR = 55°
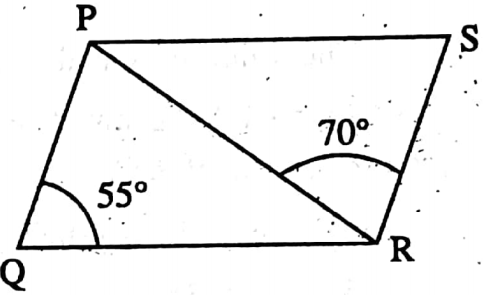
⇒ In ΔPRS, ∠RPS = 180°- ∠PSR – ∠PRS
= 180° – 55°-70° = 55°.
⇒ PS || QR and PR is intersection
∴ ∠PRQ = alternate ∠RPS = 55°
∴ The ∠PRO of the parallelogram PQRS is 55°.
Example 8. In parallelogram ABCD, AP and DP are the bisectors of ∠BAD and ∠ADC respectively, find the measures of ∠APD.
Solution: In ΔAPD,
⇒ ∠APD = 180° – (∠PAD + ∠ADP)
= 180° – \(\left(\frac{1}{2} \angle \mathrm{BAD}+\frac{1}{2} \angle \mathrm{ADC}\right)\)
= 180° – \(\frac{1}{2}\)(∠BAD + ∠ADC)
= 180° – \(\frac{1}{2}\) x 108° [DC || AB and AD is intersection]
= 90°
∴ The measures of ∠APD is 90°.
Example 9. PQRS is rectangle. Find the value of x and y.
Solution: In rectangle PQRS, PR = QS; PR and QS bisect each other.

∴ OP OQ= OR = OS
⇒ In ΔQOR, OQ = OR ∴ ∠ORQ = ∠OQR = 25°
⇒ ∠ORS = ∠QRS – ∠ORQ
⇒ x° = 90° – 25° = 65°
⇒ In, ΔROS, OR = OS, ∴ ∠OSR = ∠ORS = 65°
⇒ exterior ∠POS = ∠ORS + ∠OSR
⇒ y° = 65° + 65° = 130°
⇒ The value of x and y are 65 and 130 respectively.
Example 10. PQRS is a rectangle. Find the value of x and y.
Solution: In rectangle PQRS, PR = QS; PR and QS bisect each other,
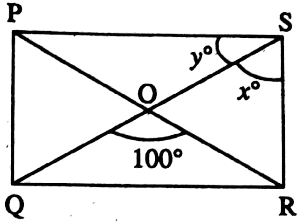
∴ OP = OQ = OR = OS
⇒ ∠ROS = 180° – ∠QOR = 180° – 100° = 80°
⇒ In, ΔROS, OR = OS
∴ ∠OSR = ∠ORS
\(x^{\circ}=\frac{180^{\circ}-\angle R O S}{2}=\frac{180^{\circ}-80^{\circ}}{2}=50^{\circ}\)
⇒ Again, ∠OSR + ∠OSP = 90°
⇒ ∠OSP = 40°
⇒ y° = 40°
∴ The value of x and y are 50 and 40 respectively.
Example 11. In parallelogram ABCD, AD (5x – 2) cm, BC = (3x + 4) cm and AB = (x + 4) cm. Find the length of DC.
Solution: In parallelogram ABCD, AD = BC

⇒ 5x – 2 = 3x + 4
⇒ 2x = 6 ⇒ x = 3
⇒ DC = AB = (x + 4) cm = (3 + 4) cm = 7cm
∴ The length of DC is 7 cm.
Example 12. In rhombus PQRS, if ∠SPQ = 60° and the perimeter is 24 cm, then find the length of diagonal PR.
Solution: In rhombus PQRS, PQ = QR = RS = SP = \(\frac{24}{4}\) cm = 6 cm
⇒ ∠SPQ = 60°
∴ ∠PQS = ∠PSQ = 60°
∴ ΔPQS is an equilateral triangle
∴ QS = PQ = 6 cm the length of diagonal PR.
⇒ Let PR and SQ meets at point O; The diagonals of a rhombus bisects each other perpendicularly.
∴ OQ = OS = \(\frac{6}{2}\) cm = 3 cm and OP = OR
⇒ In ΔPOQ, ∠POQ = 90°
⇒ PQ2 = OP2 + OQ2 [by Pythagorus theorem]
⇒ OP = \(\sqrt{P Q^2-O Q^2}=\sqrt{6^2-3^2} \mathrm{~cm}=\sqrt{27}\) cm = 3√3 cm
⇒ PR = 2 × 3√3 cm = 6√3 cm
∴ The length of diagonal PR is 6√3 cm.
