Joankessler parkland

WBBSE Solutions For Class 7 Maths  Geometry Chapter 5 Concept Of Congruency

Question 1. what is congruency?
Solution:

Congruency is the property of two geometrical Figures if one of them can be made to coincide with the other by means of reflection, transformation, translation, or rotation of their combination.

If the two Geometrical Figures are of the same shape and size they are said to be congruent to each other.

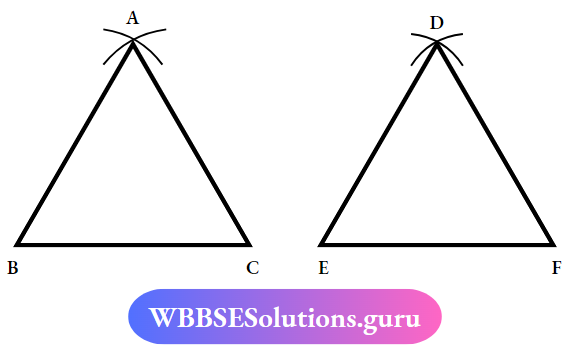
In two triangles ABC and DEF, IF AB = DE, BC= EF, CA= DF

∠A = ∠A, ∠B = ∠E, ∠C = ∠F

∴ ΔABC ≅ ΔDEF

Question 2. Write the condition of the congruence of a triangle.
Solution:

Congruence of triangle

Two triangles are said to be congruent if their respective side angles are equal and when they are placed upon one another cover each other completely.

In two triangles ABC, DEF.

Condition:

IF AB=DE, BC= EF, CA= FD, and

∠A = ∠D, ∠B = ∠E, ∠C = ∠F

∴ ΔABC ≅ ΔDEF

Question 3. What is SSS congruency of a triangle? SSS (Side-Side – Side)
Solution:

If the lengths of three sides of a triangle are equal to the lengths of three sides of the other triangle then the triangles are congruent.

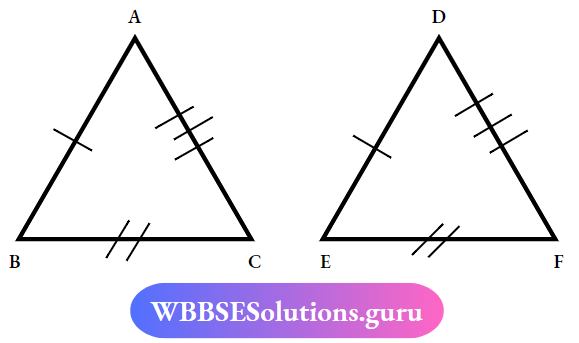
In ΔABC and ΔDEF

AB= DE, BC= EF and AC = DF

∴ ΔAB C ≅ ΔDEF

Question 4. what is the SAS congruency of a triangle SAS (Side- Angle- side)
Solution:

Two triangles are congruent if the length of two sides and the measurement of the included angle of one triangle are equal to the length of two sides and the measurement of the included angle of the other triangle

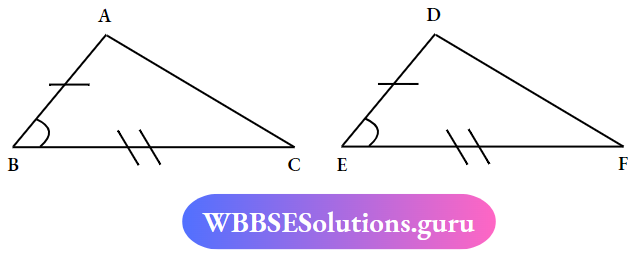
In ΔABC and ΔDEF

AB = DE, ∠ABC = ∠DEF and BC= EF

∴ ΔABC ≅ ΔDEF

Question 5. What is AAS congruency of a triangle AAS (Angle- Angle-side)
Solution:

Two triangles are congruent if the measurement of any Pair of angles and length of one pair of corresponding Sides are equal to other triangle.

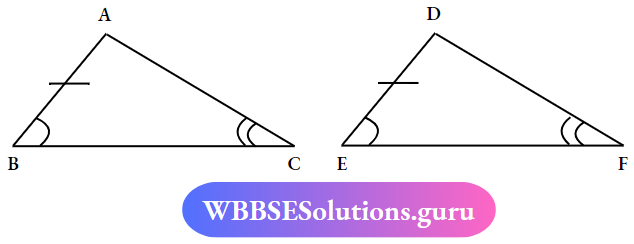
In ΔABC and ΔDEF

∠B= ∠E, ∠C = ∠F and AB = DE

∴ ΔABC ≅ ΔDEF.

Question 6. What is RHS congruency of a triangle? RHS (Right Angle- Hypotenuse – Side)
Solution:

If in two right-angled triangles, the length of the hypotenuse and the length of one triangle is equal to the length of the hypotenuse and the length of one side of the other triangle, then the two triangles are congruent.

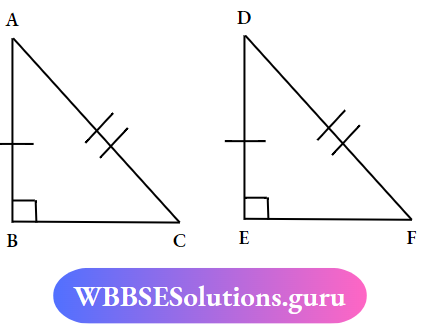
In ΔABC and ΔDEF

∠ABC ≈ ∠DEF = 90°

Hypotenuse AC = Hypotenuse DF and AB = DE

∴ ΔABC ≅ ΔDEF

Question 7. Find out whether the triangles are congruent
Solution:

AB = PQ, ∠A = ∠P

BC = QR, ∠B = ∠Q

CA = PR, ∠C = ∠R

Then the triangles are incongruent

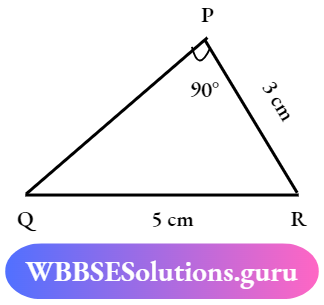
Here,

AB ≠ PQ, ∠A = ∠P

BC = QR, ∠Q ≠ ∠B

CA ≠ PR, ∠C ≠ ∠R

∴ The triangles are non- congruent.

2.

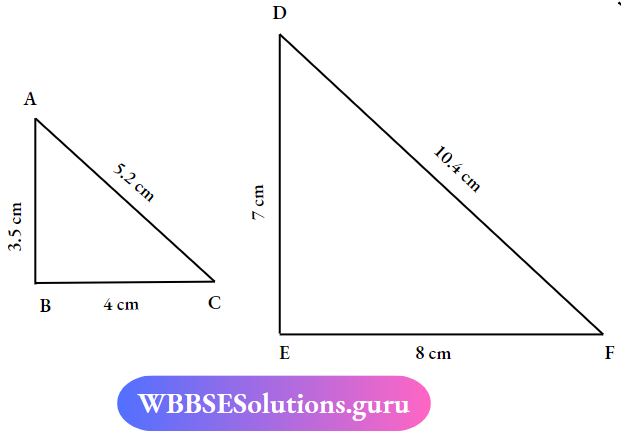
Here,

AB ≠ DE

BC ≠ EF

CA ≠ DF

∴ The ΔABC and ΔDEF are not congruent.

3.

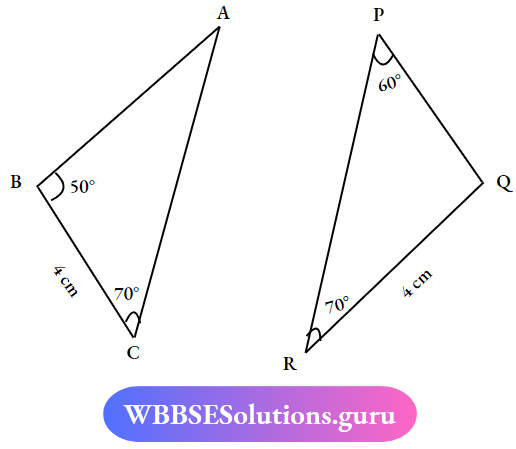
Let us Name the triangles First

BC = QR, ∠C = ∠R

∠B = ∠Q Sum of angles in a Δ^le is 180.

∠P = ∠A

According to the AAS Condition, the two triangles are in Congruence.

4.

In ΔABC and ΔDEF

∠ABC = ∠DEF = 90°

Hypotenuse AC = DF and AB = DE,

∴ ΔABC ≅ ΔDEF

5.

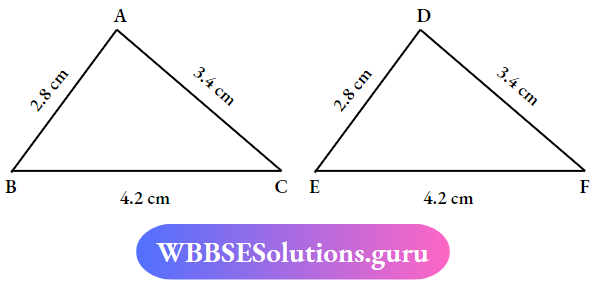
According to SSS Congruent

AB = DE

BC = EF

AC = FD

∴ ΔABC ≅ ΔDEF

6.

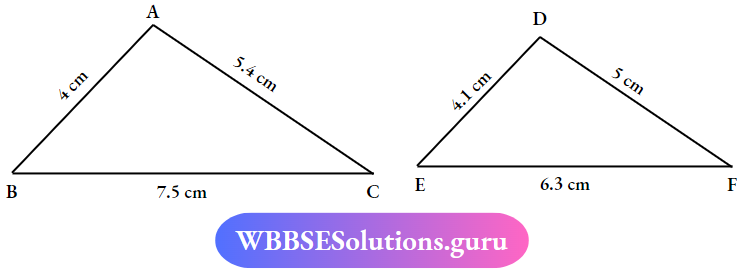
Let us Name the triangles First ΔABC, ΔDEF

Given the sides of Δ^le

AB ≠ DE

BC ≠ EF

AC ≠ FD

∴ The ΔABC and ΔDEF are non-congruent.

WBBSE Solutions For Class 7 Maths Geometry Chapter 8 Construction Of Quadrilateral

Question 1. Find the least number of data required to construct a

1. Parallelogram
2. Square
3. Rectangle and rhombus

Solution: 2. Square

Question 2. Draw a quadrilateral ABCD where AB=3.8cm, BC= 3cm, CD=4cm, AD= 2.5cm and ∠BAD=75°

Solution:

1. Draw a line AB with 3.8cm
2. Draw LBAD=75° and draw an Arc with 2.5cm. and on LBAD.
3. Draw an Arc with a radius of 3 cm from point B.
4. Draw an Arc with a radius of 4 cm from point D. where two Arcs meet Note the point as ‘c’
5. Now Join the line from B to C. and to D.
6. Now the Quadrilateral ABCD is formed.

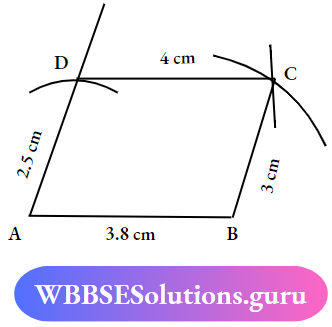
Class 7 Geometry Chapter 8 Exercise Solutions

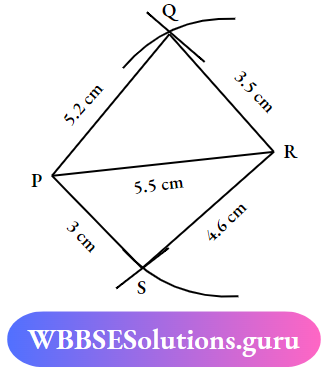
Question 3. Construct a quadrilateral PQRS in which PQ = 5.2cm, QR=3.5cm, RS= 4.6cm, SP = 3cm, and PR = 5.5cm
Solution:

1. Draw a line PR with a length of 5.5cm
2. Draw an arc with a radius of 5.2cm, from P. and draw an arc with a radius of 3.5cm from R on the above side of PR. Now mour the point as ‘Q’
3. Now Draw an arc 3cm from ‘p’ and Draw an arc with a radius of 4.6 cm
4. Now Join the mark the Joining of two arcs is Noted as ‘s’.
5. Now Join the pa and QR and also PS and RS.
6. After joining the PQ, QR, PS, and RS are formed quadrilateral PQRS.

Question 4. Construct a quadrilateral EFGH in which EH = 3.5cm, EF = 5cm, FG = 4.5 cm, ∠HEF = = 8.5° and ∠EFG =75°
Solution:

1. Draw a line EF with a length of 5 cm.
2. Make the ∠EFG = 75°, and draw aline with the angle of 75° and draw a Arc with 4.5cm From ‘F’ and make the point as ‘G’.
3. Make the ∠HEF = 85° and draw a line with the angle of 85° and draw an area with 3.5cm From E and make the point ‘H’.
4. Now Join the line ‘GH’.
5. Now the quadrilateral EFGH is formed.

WBBSE Solutions For Class 7 Maths Chapter 8 

Question 5. Construct a periodogram ABCD where AB = 4.6cm, BC = 7cm, and ∠ABC = 60°
Solution:

1. Draw a line BC with 7cm. and make the ∠ABC = 60°.
2. Draw a line through the angle ∠ABC = 60°, arc with 4.6cm, and make a point ‘A’.
3. Draw an Arc with a length of 7cm From ‘A’ and Draw another one 46cm From point ‘C’ and Joining of two Arcs marked as ‘D’.
4. Now Join the A to D and C to ‘D’
5. Now paraudogram ABCD is formed.

Question 6. Construct a rectangle PARS where pq=6cm and QR = 8cm
Solution:

1. Draw a line QR with a length of 8 cm.
2. We know that each angle in a rectangle is 90° so make 90° angle From Q and R.
3. Draw a line through the angle we know the opposite sides are equal in a rectangle.
4. Now Draw a sa arc witch 6cm from Q, on the 90° angle line as ‘p’
5. Now Draw an arc with 6cm from ‘R’ on the 90° angle line as ‘s’
6. Now Join the P, S
7. A rectangle PQRS is formed.

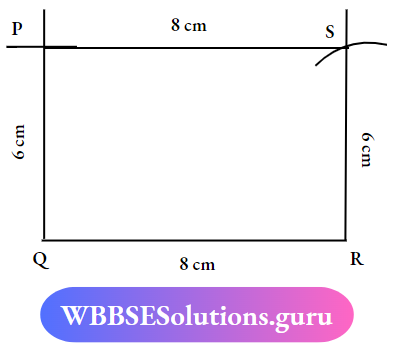
Class 7 Maths Chapter 8 Geometry PDF

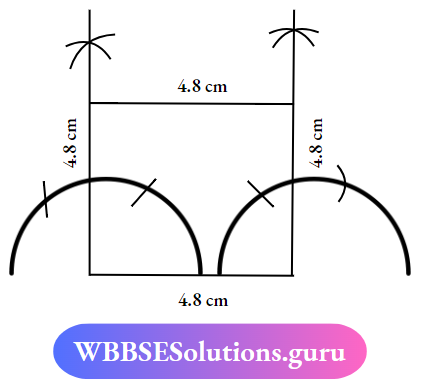
Question 7. Construct a square in which the length of each side is 4.8cm.
Solution:

1. Draw a line with a length of 4.8 cm; Now Draw a semi-circle with a radius as you like from Both Sides of the line
2. Now Take the other radius make the area on the semicircle, From the Baseline and draw another arc from the first area point
3. Now Take another radius And draw anchorages from semicircle ABC which makes the 90°
4. Now Draw an area with a length of 4.8 cm
5. Repeat the process mentioned in points 2, and, 3,4.
6. Now Joining of two Arcs drawn on a 90°angle straight line.
7. Now the square is formed with a side of 4.8 cm.

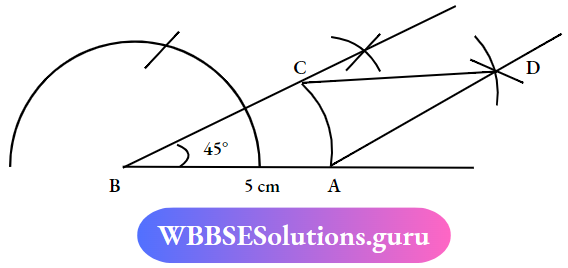
Question 8. onstruct a rhombus ABCD in which AB = 5cm) and /B = 45°.
Solution:

1. Draw a line segment AB
2. Draw an arc from point ‘B’ and make are from the line Joining Arc to the and Draw an arc with a length 5 cm from the First and une Joining at the semicircle
3. Mask the point c and point A as shown.
4. Now Draw Draw a is from ‘A’ and ‘c’ with a length of 5cm
5. Now Join Points ‘A’ and ‘D’. and also C to ‘D’.
6. ∴ ABCD is a thrombus formed.

WBBSE Class 7 Maths Geometry Chapter 8

Question 9. Construct a square PQRS in which PR= 5.2cm.
Solution:

1. Draw a line PR with a length of 5.2cm
2. Draw a semi-circle with some radius from P and Q as shown
3. Now Draw a arcs on the semicircle from the point where the Semicircle and line Join Draw another arc on two semicircles.
4. Now Draw another area from the first area on the two semicircles
5. таке another radius and draw another two areas from the First and second are on the semicircles
6. Now draw a line through the Interaction of arcs From P and Ras shown.
7. Now draw an Arc with a radius 5.2cm and from pand R Now Join the two arcs
8. Now a square PQRS is formed.

Question 10. Construct a Rectangle ABCD in which AC = 4.5cm and ∠ACB=60°
Solution:

1. Draw a line ‘C’ from ‘A’
2. Now Draw an Arc from point ‘C’ and draw another arc from the line and joining of the Arc.
3. Now Draw the arc from C and line and name it as ‘A’
4. NOW Draw an arc From A and B. The point of intersection is ‘D’
5. Now Join the line A to D and B toD.
6. ∴ The rectangle ABCD is formed.

Geometry Chapter 9 Symmetry

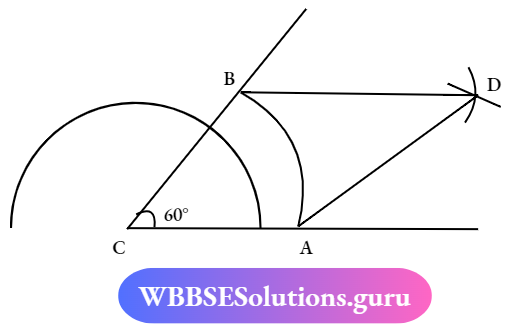
Question 1. Choose the correct answer.

1. The number of lines of symmetry of a square

1. 1
2. 2
3. 3
4. 4

∴ The option(4) 4 is the correct answer.

2. The number of lines symmetry of a circle is

1. 2
2. 3
3. 4
4. Infinite

∴ The option (4) Infinite is the correct answer.

3. There is no centre of rotation of

1. Circle
2. Rhombus
3. Isosceles trapezium
4. Equilateral triangle

∴ The option (3) Isosceles trapezium is correct answer

Read and Learn More Class 7 Maths Solutions

4. In which Figure has no line of symmetry

1. H
2. P
3. T
4. X

∴ The option (2) P is the correct answer.

Class 7 Geometry Chapter 9 Exercise Solutions

5. In which Figure has a line of symmetry and rotational symmetry both?

1. Isosceles triangle.
2. Isosceles trapezium
3. Circle
4. Parallelogram.

∴ The option (3) Circle is the correct answer

Question 2. write true or False:

1. Isosceles triangle has no line of symmetry → True

2. The number of rotational symmetry of the circle is ‘2’ → False

3. The angle of rotation of the rectangle is 90°→ False

4. The order of rotational Symmetry of a square is 4. → True

5. The largest number of lines of symmetry of a triangle is 3 → True.

Class 7 Maths Chapter 9 Geometry PDF

Question 3. Fill in the blanks:-

1. Trapezium has no Line of symmetry or rotational Symmetry

2. The number of lines of Symmetry of a regular Pentagon is  1

3. The number of lines of symmetry of an isosceles right-angled triangle is 1

4. The angle of rotation symmetry of a parallelogram is 180°

5. ______ triangle has only one line of Symmetry. Isosceles

Question 4. Which of the following figures has two lines of Symmetry and the angles or rotational symmetry is 180°
Solution:

→ Rectangle has two lines of Symmetry and angles or rotational symmetry is 180°

→ Parallelogram has no axis of Symmetry

→ It has No Angle of rotational symmetry.

→ Isosceles trapezium has 1 line of Symmetry.

→ It has No Angle of rotational symmetry

→ Square has 4 lines of symmetry

→ Angle of rotational Symmetry is +90°

Class 7 Geometry Chapter 9 Important Questions

Question 5.

1. what is symmetry?
Solution:

→Symmetry means an exact similarity in shape and size between parts of an object of a figure.

2. what is a line of symmetry?
Solution:

A figure is said to be a line of Symmetry of linear symmetry of these exists a straight line that divides into two identical halves that completely coincide with each other when folded about that line.

The straight line is called the line of symmetry of the line of reflection

3. what is rotational symmetry?
Solution:

→ In a Figure that coincides with its images when it is rotated about a point through an angle less than 360° the Figure is said to be rotational Symmetry.

The point across which the Figure rotates is called the center of rotation.

WBBSE Class 7 Maths Geometry Chapter 9 

4. what is the angle of rotational symmetry?
Solution:

For a Figure or object that has rotational symmetry the angle of turning during rotation is called the angle of rotation.

For Example: when a square is rotated by qo’ it appears the same after rotation. So the angle of rotation of the Square is 90°

Question 6. Find the angles of rotation of the following.

1. Trapezium
2. Rhombus
3. Equilateral triangle

Solution:

1. Trapezium has No out angle of rotation.
2. The rhombus has a 180° out angle of rotation.
3. An equilateral triangle has a 120° out angle of rotation

Geometry Chapter 7 Types Of Quadrilateral

Question 1. Choose the correct Answer

1. The measurement of the sum of four angles of any quadrilateral is

1. 90°
2. 180°
3. 360°
4. None of these.

∴ Option (3)360° is the correct answer

2. The each angle of a rectangle is.

1. Acute Angle
2. Right angle
3. Obtuse angle,
4. None of these

∴ Option (2) right angle is the correct answer

Read and Learn More Class 7 Maths Solutions

3. The opposite angles of the parallelogram are

1. Equal
2. Nonequal
3. Complementary
4. None of these.

∴ Option (1) equal is the correct answer

WBBSE Class 7 Maths Geometry Chapter 7

4. The angle of each square is.

1. Acute Angle,
2. Right angle,
3. Obtuse triangle
4. None of these

∴ Option (2) right angle is the correct answer.

Question 2. Write true or false

1. An isocelges trapezium is a parall dogram. → False

2. The diagonals of a rectangle bisect each other at right angles → The statement is False

3. Quadrilateral has two diagonals → The Statement is True

Question 3. Fill in the blanks:

1. The sum of the measurement of two adjacent angles of a parallelogram is 180°

2. The opposite sides of a parallelogram are Parallel to each other.

3. Quadrilateral has two diagonals

4. The length of the diagonals of an isosceles trapezium is equal.

Question 4. Each rhombus is a special type of square Explain.
Solution:

1. Every square is a rhombus (since all sides are equal and the diagonals, bisect each other at right angles
2. Not every rhombus is a square (since a rhombus does not require right angles between its sides.
3. Thus, while a square can be considered a special type of Thombus due to its right angles, a rhombus cannot be considered a type of square unless it also has right angles.

Class 7 Geometry Chapter 7 Exercise Solutions

Question 5. Write the difference between the Parallelogram and the rectangle.
Solution:

Class 7 Maths Chapter 7 Geometry PDF

Question 6. Write the difference between a rectangle and a square
Solution:

Question 7. Write the properties of the parallelogram
Solution:

Properties of parallelogram

1. Each pair of opposite sides are parallel to each other.
2. Each pair of opposite sides is equal in length
3. Each pair of opposite sides is equal in length
4. Each pair of consecutive angles sum to 180°
5. The diagonals of a parallelogram bisect each other meaning they cut each other into two equal parts.
6. The area of the parallelogram can be calculated using the formula
   1. Area = Base x Height (where Height is the perpendicular distance between the bases).
7. when transversal crosses the parallelo gram, alternate interior angles, are equal.
8. If one pair of opposite sides is both parallel and equal the quadrilateral is a parallelogram.

WBBSE Solutions for Class 7 Maths Chapter 7

Question 8. What is a convex quadrilateral, and what is a concave quadrilateral
Solution:

Convex Quadrilateral

A convex quadrilateral is a four-sided Polygon that has interior angles that measure less than 180° each The diagonals are contained entirely inside of these quadrilaterals. PQRS is a convex Quadrilateral.

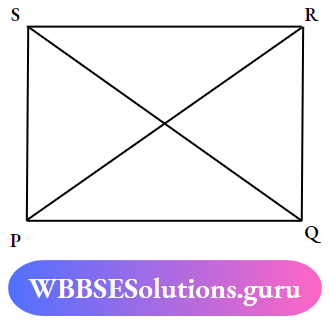
Concave Quadrilateral:

If the quadrilateral has an interior angle greater than 180° It is called a concave quadrilateral.

ABCD is a quadrilateral whose interior ∠BCD >180°