Mensuration Chapter 2 Circumference Of Circle
Some Important Facts:
In any circle:
\(\frac{Circumference}{Diameter}\) = constant (denoted by π and π = \(\frac{22}{7}\))
Read and Learn More WBBSE Solutions For Class 9 Maths
∴ circumference = π x diameter = π x 2 x radius
= πd = 2πr (d = length of the diameter, r = length of the radius)
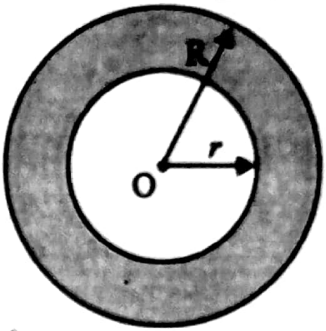
Circular ring:
Let length of the inter radius and length of outer radius = R
∴ The width of the ring = R – r.
Mensuration Chapter 2 Circumference Of Circle True Or False
Example 1. If the circumference of a circle is A cm, then its radius is \(\frac{A}{\pi}\) cm.
Solution: 2πr = A
⇒ r = \(\frac{A}{2 \pi}\)
∴ The statement is False.
Example 2. The difference of the circumference and the radius is 3.7 cm. Length of its diameter is 1.4 cm.
Solution: 2πr – R = 3.7
⇒ R(2π – 1) = 3.7
⇒ R = \(\frac{3.7 \times 7}{37}\) =0.7, 2R = 1.4 cm
∴ The statement is True.
Example 3. The width of a circular ring is 7 cm. The difference between the outer and inner circumference of the ring is 4.4 cm.
Solution: R – r = 7
∴ 2π (R – r) = 7 x 2 x \(\frac{22}{7}\) = 44
∴ The statement is False.
Example 4. Perimeter of a semi-circular ring is π (R + r) + 2(R – r) when R and r are the length of outer and inner radius.
Solution: Perimeter Outer semi-circumference + inner circumference + 2 (width)

= πR + πr + 2 (R – r)
∴ The statement is True.
Example 5. The outer and inner circumference of a ring-shaped circular plate are x cm and y cm respectively. The width of the ring-shaped plate is \(\frac{x-y}{\pi}\) cm.
Solution: 2πR – 2πr = x – y
or, R – r = \(\frac{x-y}{2 \pi}\)
∴ The statement is False.
Mensuration Chapter 2 Circumference Of Circle Fill In The Blanks
Example 1. If the circumference of a circle be 44 cm, then its length of the diameter is ________ cm.
Solution: 14.
2πr = 44 ⇒ 2r = \(\frac{44 \times 7}{22}\) = 14
Example 2. In radius of an equilateral triangle is 7 cm, so the measure of its circumradius is _______ cm.
Solution: 14 cm.
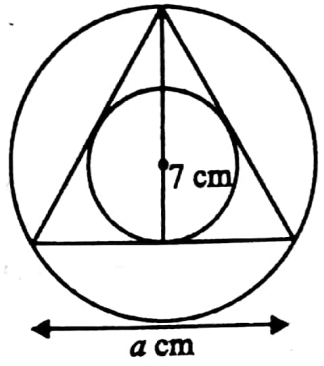
\(\frac{\sqrt{3}}{2} \times a \times \frac{1}{3}=7 \mathrm{~cm}\)
\(\frac{\sqrt{3}}{2} a=21\)
∴ \(\frac{\sqrt{3}}{2} \times \frac{2}{3}=21 \times \frac{2}{3} \mathrm{~cm}=14 \mathrm{~cm}\)
Example 3. The circumference of a circular wheel is 250 dm. The no. of revolution to move 1 km is _______
Solution: 30.
No. of revolution \(\frac{10000}{250}=30\)
Example 4. A circular wheel revolves 80 times to 8088 m. Circumference is _________
Solution: 110 cm.
Circumference = \(\frac{88}{80}\) m = 1.1 m = 110 cm.
Example 5. The diameter of a circular wheel is 3.5 mt. The distance which is carved by 1400 revolution _______
Solution: 15.4 km.
Distance covered = 1400 circumference = 1400 x \(\frac{22}{7}\) x 3.5 mt = 15.4 km
Mensuration Chapter 2 Circumference Of Circle Short Answer Type Questions
Example 1. If the perimeter of a semicircle is 180 m. Find its diameter.
Solution: If the length of the radius is r m then πr + 2r = 180
or, \(r\left(\frac{22}{7}+2\right)=180\)
or, r = \(\frac{180 \times 7}{36} \times 35 \mathrm{~m}\)
or, 2r = 70m
∴ Its diameter = 70 m.
Example 2. The length of a minute’s hand is 7 cm. How much length will Minute’s hand go to rotate 90°?
Solution: Length = \(\frac{\text { angle of centre }}{360^{\circ}}\) x circumference
= \(\frac{90^{\circ}}{360^{\circ}}\) x 2π x 7 cm = 11 cm
∴ 11 cm much length will minute hand go to rotate.
Example 3. What is the ratio of radii of the inscribed and circumscribed circle of a square?
Solution: Let length of the side of the square be a unit
Length of the circumradius = \(\frac{1}{2}\) diagonal of the square
= \(\frac{\sqrt{2}}{2}\) a unit
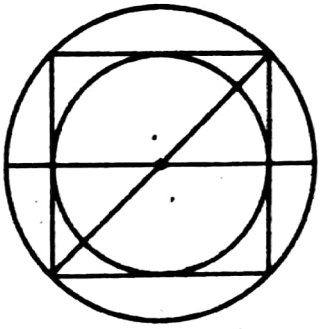
∴ Length of the inradius = \(\frac{1}{2}\) length of the side = \(\frac{a}{2}\)
ratio = \(\frac{a \sqrt{ } 2}{2}: \frac{a}{2}\) = √2:1
∴ The ratio of radii of the inscribed and circumscribed circle of a square.
Example 4. The minute’s hand of a clock is 7 cm. How length does the minute’s hand move is 15 minutes?
Solution: circumference = 2 x \(\frac{22}{7}\) x 7 cm = 44 cm
Now minute’s hand covers 44 cm in 60 minutes.
∴ In 15 minutes it covers \(\frac{44}{60}\) x 15 = 11 cm.
Example 5. What is the ratio of perimeter of a square and perimeter of a circle when the length of diameter of circle is equal to the length of the side of the square.
Solution: d = a (d is the length of the diameter and a is the length of the side of the square)
∴ Ratio = 4a: πd
= 4а: πа (d = a)
= 4 : π = 4 x 7: 22 = 14: 11
∴ The ratio of perimeter of a square and perimeter of a circle is 14: 11.
Example 6. A wire of length 36 cm is made a semi-circle. Find its length of the radius.
Solution: R (π + 2) = 36
(Length of the radius is R cm)
or, \(\frac{36 R}{7}\) = 36
⇒ R = 7 cm.
∴ The length of the radius is 7 cm.
Example 7. Circumference of a wheel is 2 m 5 dem. If the speed is 15 km/hr find the revolution of the wheel per minute.
Solution: Circumference = 25 dcm.
In 60 minute wheel covers 15 km = 150000 dcm
In 1 minute wheel covers \(\frac{150,000}{60}\)dcm = 2500 dcm
∴ No. of revolution per minute = \(\frac{2500}{25}\) = 100 dcm
∴ The revolution of the wheel per minute is 100 dcm.
Example 8. Ratio of the circumference of two circles is 2: 3 and difference of the length of radii is 2 cm. Find the smaller radius.
Solution: Let length of the smaller radius r cm.
∴ Length of bigger radius = (r + 2) cm
∴ \(\frac{2 \pi r}{2 \pi(r+2)}=\frac{2}{3}\)
⇒ 3r = 2r + 14
∴ r = 4 cm
∴ The smaller radius is 4 cm.
Example 9. If the circumference is 2π2 unit, then find its diameter.
Solution: 2πr = 2π2 ⇒ 2r = 2π
∴ Length of the diameter = 2π unit.
Example 10. The circumference of a circles is 22 cm. Then find the length of the diagonal of a square inscribed in that circle.
Solution: Let length of the radius be r cm circumference 2πr = 22 cm
∴ 2 x \(\frac{22}{7}\) x r = 22
or, r = \(\frac{7}{2}\)
Length of the side of the square = Diameter of the circle = \(\frac{7}{2}\) x 2 cm = 7 cm
∴ Length of the diagonal of the square = √2 x 7 cm = 7√2 cm.
